Краткое содержание лекции 6 |
|
|
|
|
|
|
Часть вторая. Позиционные задачи |
| |
В этой части курса будем рассматривать задачи на взаимное пересечение геометрических образов. |
|
| |
Пересечение проецирующей плоскости с плоскостью общего положения |
| |
Для определения линии пересечения проецирующей плоскости с плоскостью общего положения будем использовать собирательное свойство проецирующей плоскости.
Задача 2.1. Построить проекции линии пересечения плоскости общего положения α(ABC) с проецирующей плоскостью β (рис. 2.1 а).
Алгоритм решения
1. Определяем фронтальную проекцию линии m. Так как плоскость β - фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости β(m1 ≡ β1).
2. Горизонтальную проекцию линии m строим, исходя из условия принадлежности ее плоскости α (задача 1.2) (рис. 2.1 б). |
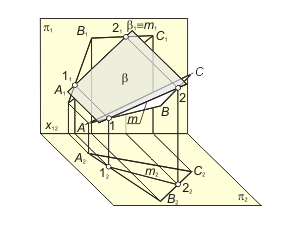
Рис. 2.1 а
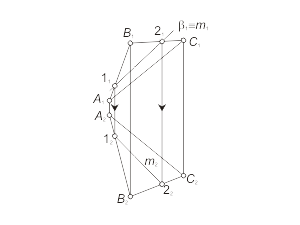
Рис. 2.1 б |
| |
Пересечение прямой линии с плоскостью |
| |
а) Прямая и плоскость общего положения
Для построения точки пересечения прямой l с плоскостью α необходимо:
1. Заключить прямую l во вспомогательную плоскость β (рис. 2.2). Как правило, плоскость β - проецирующая плоскость.
2. Построить линию пересечения заданной плоскости α и вспомогательной плоскости β - прямую m.
3. Определить точку пересечения K прямой линии l с построенной линией m.
Так как линия m принадлежит заданной плоскости α, следовательно, точка K будет искомой точкой пересечения прямой l с плоскостью α.
Задача 2.2. Построить проекции точки пересечения прямой общего положения l с плоскостью общего положения α(ABC) (рис. 2.3).
Алгоритм решения
1. Заключаем прямую линию l во вспомогательную проецирующую плоскость β. Так как плоскость β - фронтально-проецирующая, то первая проекция линии l совпадает с вырожденной проекцией плоскости β (l1 ≡ β1).
2. Строим линию пересечения m заданной плоскости α и вспомогательной плоскости β в соответствии с алгоритмом решения задачи 2.1.
3. Определяем точку пересечения K прямой линии l с построенной линией m следующим образом (рис. 2.4):
- отмечаем проекцию K2 (K2 = l2 ∩ m2);
- на пересечении l1 и линии проекционной связи отмечаем проекцию K1.
4. Определяем видимость прямой l относительно плоскости α (рис. 2.5 а).
Точка K делит прямую l на две части – видимую и невидимую (плоскость α считаем бесконечной и непрозрачной). Невидимая часть прямой может быть за плоскостью при проецировании на π1 и под плоскостью при проецировании на π2. Невидимую часть прямой будем отмечать на эпюре Монжа штриховой линией. Для определения видимости прямой при проецировании на плоскость π1 используются конкурирующие точки 1 и 3. На основании расположения горизонтальных проекций 12 и 32 можно сделать вывод, что точка 3, принадлежащая l - видимая. Следовательно, часть прямой, содержащая точку 3, находится перед плоскостью. На π1 этот участок прямой l отмечается основной линией. Для определения видимости прямой при проецировании на плоскость π2 используются конкурирующие точки 4 и 5. На основании расположения фронтальных проекций 41 и 51 можно сделать вывод, что точка 4, принадлежащая l - видимая. Следовательно, часть прямой, содержащая точку 4, находится над плоскостью. На π2 этот участок прямой l отмечается основной линией.
б) Прямая - проецирующая, плоскость – общего положения
Задача. Построить проекции точки пересечения проецирующей прямой l с плоскостью общего положения α(a || b) (рис. 2.6). При решении задачи будем использовать алгоритм построения точки, принадлежащей плоскости.
Алгоритм решения
1. Так как прямая l - горизонтально-проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью будет совпадать с вырожденной проекцией прямой l. Отмечаем горизонтальную проекцию K2 ≡ l2 .
2. Фронтальную проекцию K1 определяем из условия принадлежности точки K плоскости α (задача 1.4).
в) Прямая - общего положения, плоскость – проецирующая
Задача. Построить проекции точки пересечения прямой общего положения l с проецирующей плоскостью α (рис. 2.7).
Алгоритм решения
1. Так как точка K общий элемент прямой и плоскости, а плоскость α фронтально-проецирующая, следовательно, проекция K1 будет определяться на пересечении фронтальных проекций прямой и плоскости (K1 = l1 ∩ α1).
2. Горизонтальную проекцию K2 определяем из условия принадлежности точки K прямой l (задача 1.1).
|
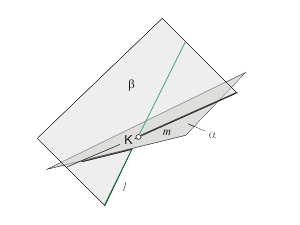
Рис. 2.2
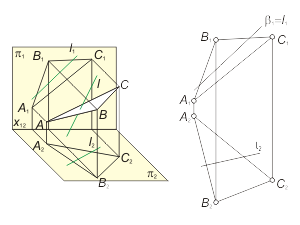
Рис. 2.3
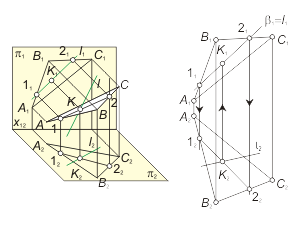
Рис. 2.4
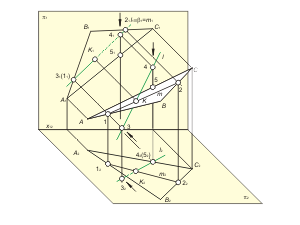
Рис. 2.5 а
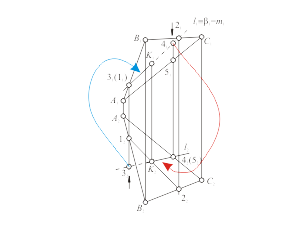
Рис. 2.5 б
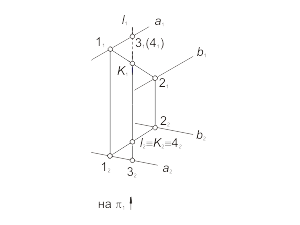
Рис. 2.6
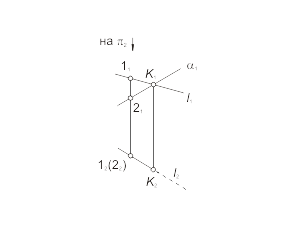
Рис. 2.7 |
| |
Пересечение проецирующей плоскости с поверхностью общего положения |
| |
Для определения линии пересечения проецирующей плоскости с поверхностью общего положения будем использовать собирательное свойство проецирующей плоскости.
Задача 2.3. Построить проекции линии пересечения проецирующей плоскостью β с поверхностью общего положения Φ(f, S) с (рис. 2.8).
Алгоритм решения
1. Определяем фронтальную проекцию линии m. Так как плоскость β - фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости β (m1 ≡ β1).
2. Горизонтальную проекцию линии m строим, исходя из условия принадлежности ее поверхности Φ(f, S).
|
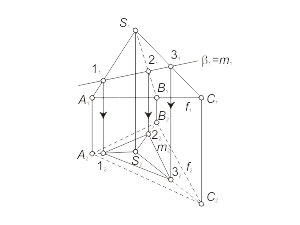
Рис. 2.8 |
| |
Пересечение прямой линии с поверхностью |
| |
а) Прямая и поверхность - общего положения
Для построения точки пересечения прямой l с поверхностью Φ необходимо:
1. Заключить прямую l во вспомогательную плоскость β (рис. 2.9). Как правило, плоскость β - проецирующая плоскость.
2. Построить линию пересечения заданной поверхности Φ и вспомогательной плоскости β - линию m.
3. Определить точку (точки) пересечения прямой l с построенной линией m.
Так как линия m принадлежит заданной поверхности Φ, следовательно, точка K будет искомой точкой пересечения прямой l с поверхностью Φ.
Задача 2.4. Построить проекции точек пересечения прямой общего положения l с поверхностью общего положения Φ(f, S).
Алгоритм решения
1. Заключаем прямую линию l во вспомогательную проецирующую плоскость β (рис. 2.10). Так как плоскость β фронтально-проецирующая, то первая проекция линии l совпадает с вырожденной проекцией плоскости β (l1 ≡ β1).
2. Строим линию пересечения m заданной плоскости α и вспомогательной плоскости β в соответствии с алгоритмом решения задачи 2.3.
3. Определяем точки пересечения K, L прямой линии l с построенной линией m следующим образом (рис. 2.11):
- отмечаем проекции K2, L2 (K2, L2 = l2 ∩ m2);
- на пересечении l1 и линий проекционной связи отмечаем проекции K1 и L1.
4. Определяем видимость прямой l относительно плоскости α. Невидимая часть прямой может быть за поверхностью при проецировании на π1 и под поверхностью при проецировании на π2.
Невидимую часть прямой будем отмечать на эпюре Монжа штриховой линией. Для определения видимости прямой при проецировании на плоскость π1 используются конкурирующие точки 1 и 4, а также точки 3 и 5 (рис. 2.12). На основании расположения горизонтальных проекций 12 и 42 можно сделать вывод, что точка 3, принадлежащая l - видимая. Следовательно, часть прямой от точки 4 до точки K находится перед поверхностью. На π1 этот участок прямой l отмечается основной линией. На основании расположения горизонтальных проекций 32 и 52 можно сделать вывод, что точка 5, принадлежащая l - невидимая. Следовательно, часть прямой от точки K до точки 5 находится за поверхностью. На π1 этот участок прямой l отмечается штриховой линией. Для определения видимости прямой при проецировании на плоскость π2 используются конкурирующие точки 6 и 7, а также точки 8 и 9 (рис. 2.13). На основании расположения фронтальных проекций 61 и 71 можно сделать вывод, что точка 6, принадлежащая l - видимая. Следовательно, часть прямой, содержащая точку 6, находится над поверхностью. На π2 этот участок прямой l отмечается основной линией. Аналогично определяется видимость участка прямой l, содержащего точку 8.
б) Прямая - проецирующая, поверхность – общего положения
Задача. Построить проекции точек пересечения проецирующей прямой l с поверхностью общего положения Φ(f, h) (рис. 2.14).
При решении задачи будем использовать алгоритм построения точки, принадлежащей поверхности.
Алгоритм решения
1. Так как прямая l горизонтально- проецирующая, то вторые проекции точек пересечения прямой с поверхностью будет совпадать с вырожденной проекцией прямой l. Отмечаем горизонтальные проекции K2, L2 ≡ l2.
2. Фронтальные проекции K1, L1 определяем из условия принадлежности точек K, L поверхности Φ(i, f) (задача 1.5).
в) Прямая - общего положения, поверхность – проецирующая
Задача. Построить проекции точек пересечения прямой общего положения l с проецирующей поверхностью Φ(f, S) (рис. 2.15).
Алгоритм решения
1. Так как точки K, L общие для прямой и поверхности, а поверхность Φ(f, S) – горизонтально-проецирующая, следовательно, проекции K2, L2 будут определяться на пересечении горизонтальных проекций прямой и поверхности (K2, L2 = l2 ∩ Φ2).
2. Фронтальные проекции K1, L1 определяем из условия принадлежности точек K, L прямой l (задача 1.1).
|
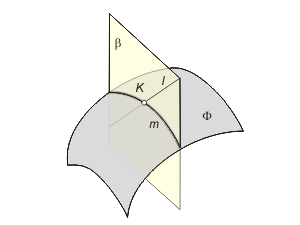
Рис. 2.9

Рис. 2.10
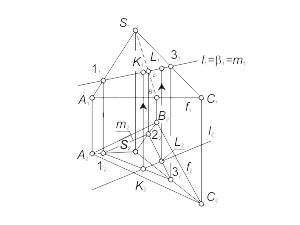
Рис. 2.11
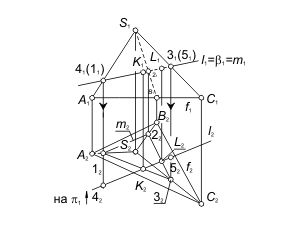
Рис. 2.12
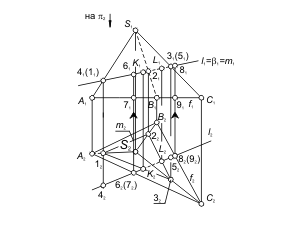
Рис. 2.13
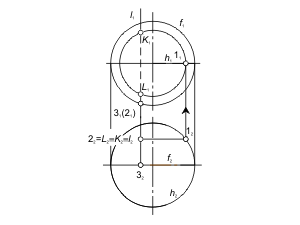
Рис. 2.14
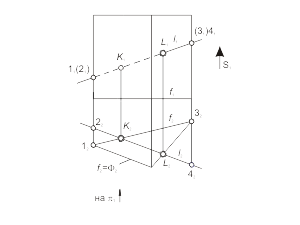
Рис. 2.15
|
| |
| |
|
|
|
|

















