Краткое содержание лекции 7
 
Пересечение поверхностей
 
Для построения линии пересечения поверхностей будем использовать следующие способы:

1. Алгоритм построения линии принадлежащей поверхности.
2. Способ вспомогательных секущих плоскостей.
3. Способ вспомогательных концентрических сфер.

 
 
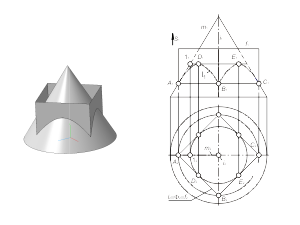
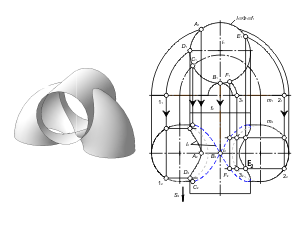
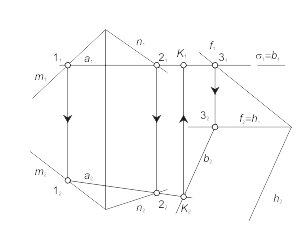
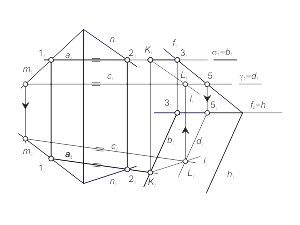
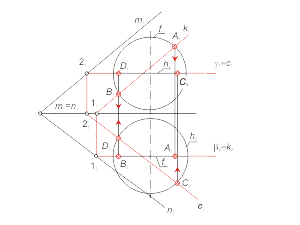
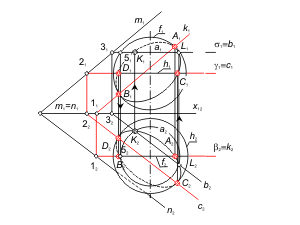
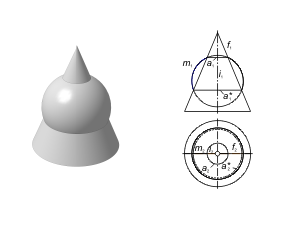
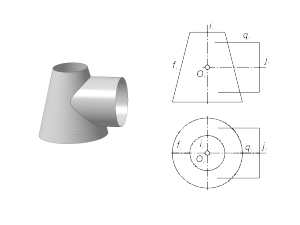
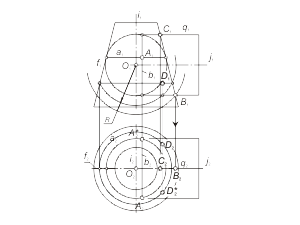
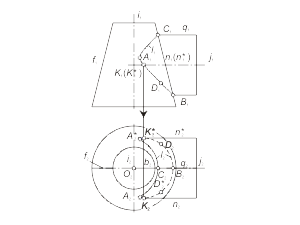
Алгоритм построения линии принадлежащей поверхности
 
Этот способ используется в том случае, если одна из двух заданных поверхностей – проецирующая. Для определения линии пересечения поверхностей будем использовать собирательное свойство проецирующей поверхности.

Задача. Построить проекции линии пересечения l проецирующей призматической поверхности Φ (f, S) с поверхностью общего положения Γ (i, m) (рис. 2.16).

Алгоритм решения

1. Так как призматическая поверхность Φ (f, S) - горизонтально-проецирующая, то вторая проекция линии пересечения поверхностей будет совпадать с вырожденной горизонтальной проекцией поверхности Φ. Отмечаем горизонтальную проекцию l2 ≡ Φ2 ≡ f2.
2. Фронтальную проекцию l1 определяем из условия принадлежности линии l поверхности Γ (i, m).

Задача. Построить проекции линии пересечения l проецирующей цилиндрической поверхности Φ (f, S) с торовой поверхностью Γ (i, m) (рис. 2.17).

Алгоритм решения

1. Так как поверхность Φ (f, S) - фронтально-проецирующая, то первая проекция линии пересечения поверхностей будет совпадать с вырожденной фронтальной проекцией поверхности Φ. Отмечаем фронтальную проекцию l1 ≡ Φ1 ≡ f1 .
2. Горизонтальную проекцию l2 определяем из условия принадлежности линии l поверхности тора - Γ (i, m).

Рис. 2.16

Рис. 2.17
 
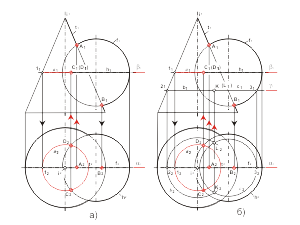
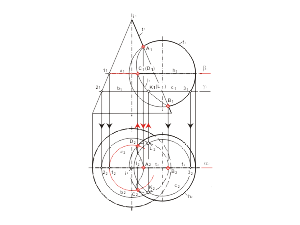
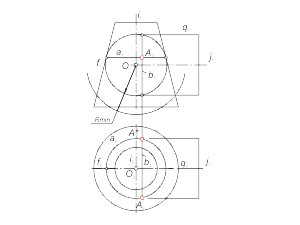
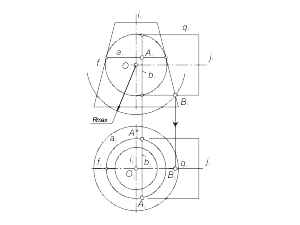
Способ вспомогательных секущих плоскостей
 

Этот способ рационально применять тогда, когда есть возможность пересечь обе поверхности плоскостью по графически простым линиям (прямым, окружностям).

Задача 2.5. Построить линию пересечения l поверхности Φ с поверхностью Γ (рис. 2.18).

Алгоритм решения

1. Рассекаем обе поверхности вспомогательной плоскостью σ.
2. Определяем линию пересечения a плоскости σ с поверхностью Φ a = σ ∩ Φ.
3. Определяем линию пересечения b плоскости σ с поверхностью Γ (b = σ ∩ Γ).
4. Находим точки пересечения построенных линий a и b (K, L = a ∩ b).

Для построения других точек искомой линии повторяем указанный алгоритм необходимое количество раз.

Задача. Построить проекции линии пересечения l плоскости α (m, n) с плоскостью β (f, h) (рис. 2.19). Для решения этой задачи в качестве вспомогательных плоскостей можно использовать, например, плоскости уровня σ и γ параллельные π2.

Алгоритм решения

1. В соответствии с алгоритмом решения задачи 2.5 определяем проекции одной общей точки заданных плоскостей – точки K (K = a ∩ b) (рис. 2.19 а).
2. Аналогично определяем проекции точки L (L = c ∩ d) (рис. 2.19 б ).
3. Через проекции точек K и L проводим соответствующие проекции искомой прямой l.

Задача. Построить проекции линии пересечения l поверхности Φ (f, h) с плоскостью α (m, n) (рис. 2.20).

Для решения этой задачи в качестве вспомогательных плоскостей можно использовать плоскости уровня, т.к. одна из проекций линии пересечения такой плоскости со сферой будет представлять собой прямую, а вторая – окружность.

Алгоритм решения

1. Определяем проекции точек изменения видимости линии l .
а) Строим проекции точек A и B, используя в качестве вспомогательной плоскости – плоскость β (β || π1):


– определяем проекции линии пересечения плоскости β со сферой – окружность f (f1, f2);
– определяем проекции линии пересечения плоскости β с плоскостью α в соответствии с алгоритмом решения задачи 2.1 – прямая k (k1, k2);
– отмечаем проекции точек A и B: A1, B1 = k1 ∩ f1; A2, B2 ~ β2


б) Строим проекции точек С и D , используя в качестве вспомогательной плоскости плоскость уровня γ (γ || π2) :


– определяем проекции линии пересечения плоскости γ со сферой – окружность h (h1, h2) ;
– определяем проекции линии пересечения плоскости γ с плоскостью α в соответствии с алгоритмом решения задачи 2.1 – прямая c (c1, c2);
– отмечаем проекции точек C и D: C2, D2 = c2 ∩ h2; C1, D1 ~ γ1


2. В соответствии с алгоритмом решения задачи 2.5 определяем произвольные общие точки (K и L) заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня σ (σ || π2) (рис. 2.21):


– определяем проекции линии пересечения плоскости σ со сферой в соответствии с алгоритмом решения задачи 2.3 – окружность a (a1, a2);
– определяем проекции линии пересечения плоскости σ с плоскостью α в соответствии с алгоритмом решения задачи 2.1 – прямая b (b1, b2);
– отмечаем проекции точек K и L: K, L = a ∩ b; K2, L2 = a2 ∩ b2; K1, L1 ~ σ1. Для построения других точек искомой линии l повторяем последовательность построений пункта 2 данной задачи.


3. Для определения видимости линии l будем использовать точку K. При проецировании на плоскость π1 точка K будет принадлежать невидимой части сферы, следовательно, часть линии l от точки A до точки B, содержащая точку K, будет невидимой. В поле проекций π1 этот участок (A1, K1, D1, B1) отмечен штриховой линией. При проецировании на плоскость π2 точка K будет принадлежать видимой части сферы, следовательно, часть линии l от точки C до точки D, содержащая точку K, будет видимой. В поле проекций π2 этот участок (C2, A2, K2, D2) отмечен сплошной основной линией.

Задача. Построить проекции линии пересечения конической поверхности Φ (i, t) со сферой Γ (f, h).

Для решения этой задачи в качестве вспомогательных плоскостей можно использовать плоскости уровня, параллельные π2, т.к. одна из проекций линии пересечения такой плоскости с заданными поверхностями будет представлять собой прямую, а вторая – окружность.

Алгоритм решения

1. Определяем проекции точек изменения видимости линии l (рис. 2.22 а).


а) Строим проекции точек A и B, используя в качестве вспомогательной плоскости плоскость α (α || π1):


– определяем проекции линии пересечения плоскости α со сферой – окружность f (f1, f2);
– определяем проекции линии пересечения плоскости α с конической поверхностью вращения – прямая t (t1, t2);
– отмечаем проекции точек A и B: A1, B1 = t1 ∩ f1; A2, B2 ~ α2.


б) Строим проекции точек С и D, используя в качестве вспомогательной плоскости плоскость уровня β (β || π2) :


– определяем проекции линии пересечения плоскости β со сферой – окружность h (h1, h2);
– определяем проекции линии пересечения плоскости β с конической поверхностью вращения – окружность a (a1, a2);
– отмечаем проекции точек C и D: C2, D2 = a2 ∩ h2; C1, D1 ~ β1.


2. Определяем произвольные общие точки (K и L) заданных фигур, используя в качестве вспомогательной плоскости плоскость уровня γ (γ || π2) (рис. 2.22 б):


– определяем проекции линии пересечения плоскости γ с конической поверхностью вращения – окружность b (b1, b2);
– определяем проекции линии пересечения плоскости γ со сферой – окружность с (с1, с2);
– отмечаем проекции точек K и L: K, L = b ∩ c; K2, L2 = b2 ∩ c2; K1, L1 ~ γ1.


Для построения других точек искомой линии l повторяем последовательность построений пункта 2 данной задачи.

3. Определение видимости линии l.

При проецировании на плоскость π1 видимая и невидимая часть линии l будут совпадать. При проецировании на плоскость π2 видимость линии можно определить, например, по положению точки A. Точка A будет принадлежать видимой части сферы, следовательно, часть линии l от точки C до точки D, содержащая точку A будет видимой. В поле проекций π2 этот участок (C2, A2, D2) отмечен сплошной основной линией (рис. 2.23).

Рис. 2.18

Рис. 2.19 а

Рис. 2.19 б

Рис. 2.20

Рис. 2.21

Рис. 2.22

 

Рис. 2.23
 
Способ вспомогательных концентрических сфер
 

Этот способ можно применять только для определения линии пересечения поверхностей вращения, оси вращения которых пересекаются, и поверхности имеют общую плоскость симметрии. Способ сфер основан на следующем определении: две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения (рис 2.24).

Задача. Построить проекции линии пересечения l поверхности Φ (i, f) с поверхностью Γ (j, q) (рис. 2.25).

Для определения общих точек заданных поверхностей будем пересекать их сферами с центрами в точке пересечения осей вращения этих поверхностей (О = i ∩ j).

Алгоритм решения

1. Строим фронтальный очерк сферы наименьшего радиуса. Сферой наименьшего радиуса (Rmin) является наибольшая из двух сфер, касательных к образующим заданных поверхностей. На эпюре Монжа этой сфере соответствует окружность, касательная к фронтальным очерковым прямым конической поверхности (рис. 2.26). Сфера касается конической поверхности по окружности а и пересекает цилиндрическую поверхность по окружности b. При этом плоскости окружностей а и b перпендикулярны осям вращения i и j соответственно. Одна из общих точек поверхностей определится на пересечении этих окружностей: A = a ∩ b; A1 = a1 ∩ b1; A2 ~ a2.

2. Строим фронтальный очерк сферы наибольшего радиуса. Радиусу наибольшей сферы (Rmax) на фронтальной проекции соответствует расстояние от точки О1 до наиболее удаленной точки пересечения очерков заданных поверхностей (B1) (рис. 2.27).

3. Строим фронтальный очерк сферы произвольного радиуса из диапазона Rmin ≤ R ≤ Rmax (рис. 2.28). Сфера радиуса R пересекает коническую и цилиндрическую поверхность по окружностям с и d соответственно. На пересечении этих окружностей определится еще одна общая точка заданных поверхностей – точка D: D = c ∩ d; D1 (D*1) = c1 ∩ d1; D2(D*2) ~ c2. Для построения других точек искомой линии l повторяем последовательность построений пункта 3 данной задачи.

4. Определяем проекции точек изменения видимости линии l при проецировании на плоскость π2 (рис. 2.29). Вначале отмечаем фронтальные проекции точек изменения видимости линии l: K1 (К*1)= l1 ∩ n1(n*1). Горизонтальные проекции К2 (К*2) будут принадлежать соответствующим горизонтальным очерковым прямым n2 (n*2) цилиндрической поверхности.

Рис. 2.24

Рис. 2.25

Рис. 2.26

Рис. 2.27

Рис. 2.28

Рис. 2.29
 
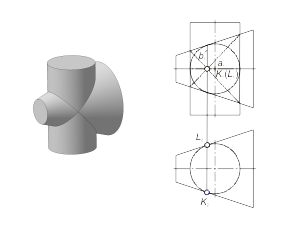
Частные случаи пересечения поверхностей вращения второго порядка
 
К поверхностям второго порядка относятся линейчатые поверхности вращения, а также поверхности, образованные вращением кривой второго порядка вокруг оси симметрии этой кривой.

Теорема Монжа

Если две поверхности второго порядка вписаны в третью поверхность второго порядка или описаны вокруг нее, то линия их пересечения распадается на две кривые второго порядка. На рис.2.30 изображены цилиндрическая и коническая поверхности вращения, описанные вокруг сферы.

Цилиндрическая и коническая поверхности касаются сферы по окружностям a и b, которые пересекаются в точках K и L. Через эти точки и будут проходить линии пересечения рассматриваемых поверхностей.

Рис. 2.30