Краткое содержание лекции 5
 
Поверхности вращения
 
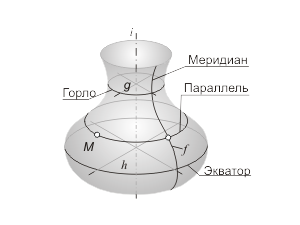
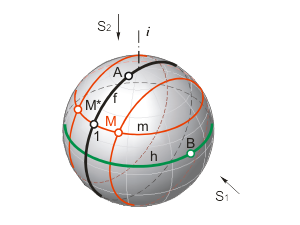
Поверхность вращения образуется вращением какой-либо линии (образующей) вокруг неподвижной оси. Как правило, ось вращения располагается перпендикулярно одной из плоскостей проекций (рис. 1.43). Если образующая поверхности вращения - прямая линия, то образуется линейчатая поверхность. В противном случае поверхность вращения будет относиться к классу нелинейчатых поверхностей.

Репер поверхности включает в себя ось вращения i и образующую линию f. Каждая точка образующей линии вращается по окружности, которая называется параллелью. Плоскость этой параллели перпендикулярна оси вращения, а центр принадлежит оси вращения. Параллель наибольшего радиуса называется экватором, а параллель наименьшего радиуса – горлом. Меридиан – линия на поверхности, расположенная в одной плоскости с осью вращения. Главный меридиан – меридиан, плоскость которого параллельна плоскости проекций. Если ось вращения перпендикулярна плоскости π2, то главный меридиан параллелен π1. Если же ось вращения перпендикулярна плоскости π1, то главный меридиан параллелен π2. Один из очерков поверхности вращения определяется главным меридианом, а второй – экватором или экватором и горлом.

Рис. 1.43
 
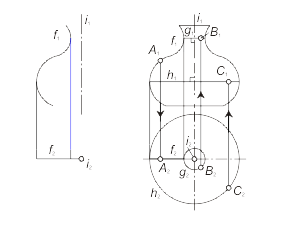
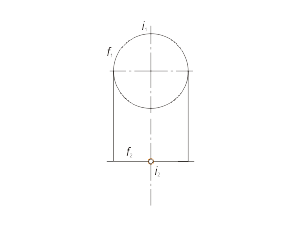
Моделирование поверхности вращения общего вида
 

Для построения модели поверхности вращения необходимо задать на эпюре Монжа проекции ее репера: оси вращения i и образующей линии f (рис. 1.44 а), а также решить задачу построения произвольной точки поверхности. Дополним эпюр фронтальным и горизонтальным очерками поверхности. На рис. 1.44 б основной линией изображены очерки поверхности, а также отмечены проекции точек A, B и C принадлежащих главному меридиану, горлу и экватору соответственно.


Рис. 1.44

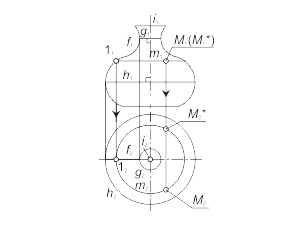
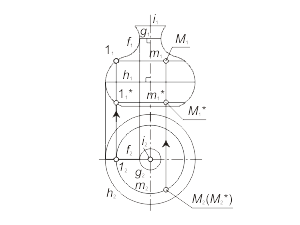
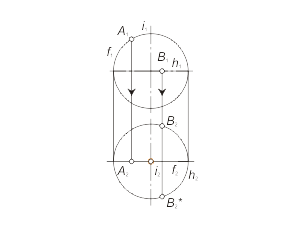
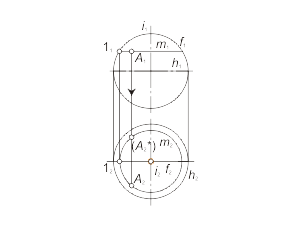
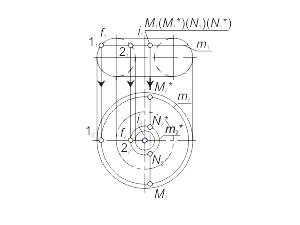
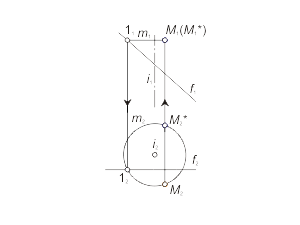
Задача 1.5 Построить произвольную точку M, принадлежащую поверхности вращения Φ(i, f).

Алгоритм решения 1

1. Отмечаем произвольно проекцию M1 точки M (рис. 1.45 а).
2. Через M1 перпендикулярно i1 проводим проекцию m1 параллели m, принадлежащей поверхности Φ .
3. Находим проекцию 11 точки пересечения параллели m с образующей f.
4. Строим проекцию m2 – окружность с центром в точке i2, проходящая через точку 12.
5. Через точку M1 проводим линию проекционной связи и при пересечении ее с окружностью m2 отмечаем две точки – проекцию M2 точки M видимой части поверхности и M2* точки M*, принадлежащей невидимой части поверхности Φ.

Алгоритм решения 2

1. Отмечаем произвольно проекцию M2 точки M (рис. 1.45 б).
2. Через M2 строим окружность m2 с центром в точке i2.
3. Находим проекцию 12 точки пересечения параллели m с образующей f.
4. Строим проекции m1 и m1*– прямые перпендикулярные i1, проходящие через точки 11 и 11* соответственно.
5. Через точку M2 проводим линию проекционной связи и при пересечении ее с прямыми m1 и m1* отмечаем точки M1 и M1*– проекции точек M и M* видимой и невидимой части поверхности Φ соответственно. Приведённые алгоритмы решения подобной задачи применимы для любой поверхности вращения. В зависимости от формы образующей линии f могут получаться различные виды поверхности вращения.

Рис. 1.45 a

Рис. 1.45 б
 
Моделирование сферы
 

Сфера образуется вращением окружности вокруг одного из ее диаметров (рис. 1.46 а). Один из реперов сферы – ось вращения i и образующая окружность f (рис. 1.46 б). Сфера также может быть задана экватором h и главным меридианом f (рис.1.46 в).

На рис. 1.46 г показано построение точки A, принадлежащей сфере Φ(i, f). Построение выполнено по первому алгоритму задачи 1.5.

Рис. 1.46 a

Рис. 1.46 б

Рис. 1.46 в

Рис. 1.46 г
 
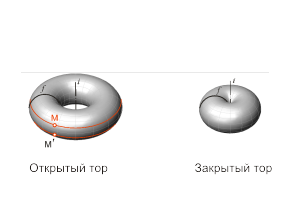
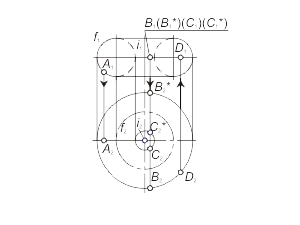
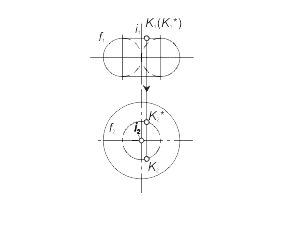
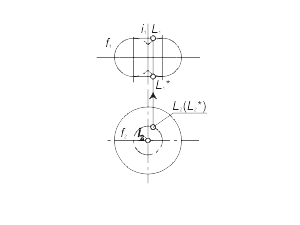
Моделирование торовой поверхности
 

Торовая поверхность образуется вращением окружности вокруг оси, которая расположена в плоскости окружности, но не проходит через ее центр (рис. 1.47).

Репером торовой поверхности будут ось вращения i и образующая окружность f. На рисунках 1.48 а, б, в изображены три модели торовой поверхности в зависимости от взаимного положения оси вращения и образующей окружности, а также модели точек, принадлежащих контурным линиям торовой поверхности. Если ось вращения i не пересекает образующую окружость f, то образуется открытый тор (кольцо) (рис. 1.48 а). Если же ось вращения i касается образующей окружости f или пересекает ее, то образуется закрытая торовая поверхность (рис. 1.48 б, в).

На рисунке 1.49 а показано построение произвольной точки M, принадлежащей торовой поверхности Φ(i, f). Построение выполняется по первому алгоритму задачи 1.5. На рис. 1.49 б показано построение точки M по второму алгоритму задачи 1.5.

Рис. 1.47

Рис. 1.48 а

Рис. 1.48 б

Рис. 1.48 в

Рис. 1.49 а

Рис. 1.49 б
 
Линейчатые поверхности вращения
 
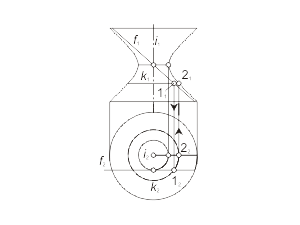
При вращении прямой линии, которая пересекает ось вращения в собственной или несобственной точке, образуются, соответственно, коническая или цилиндрическая поверхности. Если прямая линия f скрещивается с осью вращения i, то получается поверхность, называемая однополостным гиперболоидом вращения. Эта поверхность может быть получена также путём вращения гиперболы вокруг её мнимой оси. На рисунке 1.50 а показано построение произвольной точки M, принадлежащей поверхности однополостного гиперболоида вращения Φ(i, f), а на рис. 1.50 б) – построение фронтального очерка заданной поверхности. Через точку 1, принадлежащую образующей прямой f, проводится параллель k поверхности вращения, после чего определяется точка 2, принадлежащая главному меридиану. Аналогично строятся все остальные точки гиперболы.

Рис. 1.50 а

Рис. 1.50 б