|
||||
 |
||||
| к лекции 2 | ||||
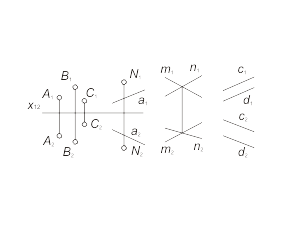
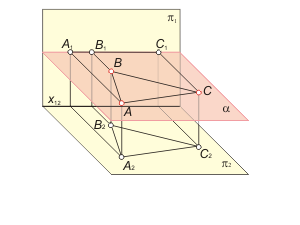
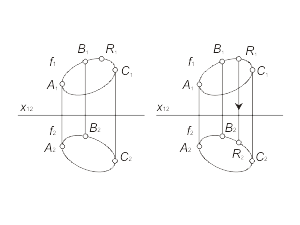
Способы задания плоскости (рис. 1.20):
1. Три точки, не лежащие на одной прямой - α(A, B, C). 2. Прямая и точка не принадлежащая этой прямой - α(N, a). 3. Две пересекающиеся или две параллельные прямые - α(m, n), α(c, d). |
Рис. 1-20 |
|||
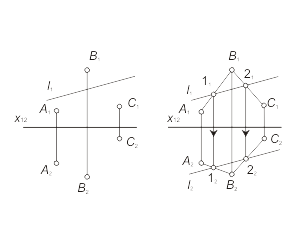
Задача 1.2 Построить модель какой-либо прямой, принадлежащей плоскости α(А, В, С). Прямая принадлежит плоскости, если она проходит через две точки этой плоскости. |
Рис. 1-21 |
|||
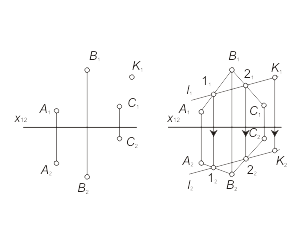
Задача 1.3 Построить модель произвольно взятой точки К, принадлежащей плоскости α(А, В, С). Построение недостающей проекции точки, принадлежащей плоскости, основано на условии принадлежности этой точки прямой, лежащей в плоскости. Алгоритм решения: |
Рис. 1-22
|
|||
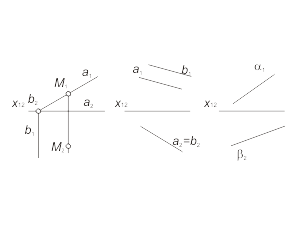
Плоскости частного положения Проецирующие плоскости Плоскость, проходящая через проецирующую прямую, называется проецирующей плоскостью. Очевидно, что фронтально-проецирующая плоскость перпендикулярна плоскости π1 (рис. 1.23), а горизонтально-проецирующая плоскость перпендикулярна π2. На рис. 1.23 видно, что фронтальные проекции всех элементов плоскости α(a,b) расположены на одной прямой a1. Эта прямая называется вырожденной проекцией плоскости и обладает собирательным свойством. На рис. 1.24 представлены проекции фронтально-проецирующей плоскости α и горизонтально-проецирующей плоскости β. |
Рис. 1-23 Рис. 1-24 |
|||
На рис. 1.25 изображена плоскость α, параллельная горизонтальной плоскости проекций. Треугольник ABC, принадлежащий плоскости α, на плоскость π2 будет проецироваться без искажения, т.е. по горизонтальной проекции треугольника можно судить об его истинных размерах. На рис. 1.26 представлены проекции плоскости уровня α, параллельной плоскости π2, и плоскости β, параллельной плоскости π1. |
Рис. 1-25 Рис. 1-26 |
|||
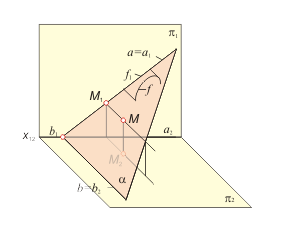
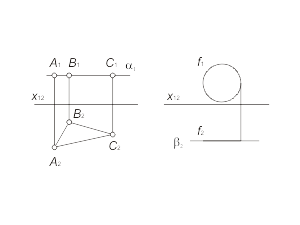
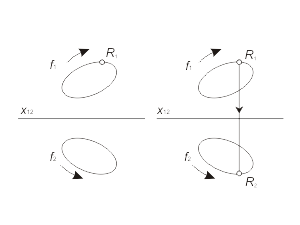
Кривую линию можно рассматривать как траекторию движущейся точки или как совокупность точек, обладающих каким-либо общим для них свойством. Кривая линия может являться результатом взаимного пересечения поверхностей. Кривая линия может быть плоской или пространственной. Если все точки кривой расположены в одной плоскости, то такая линия называется плоской. Кривая линия, которая не может быть совмещена с плоскостью всеми своими точками, называется пространственной, например винтовая линия. Моделью кривой линии в общем случае является пара кривых линий f(f1, f2) (рис. 1.27 а).
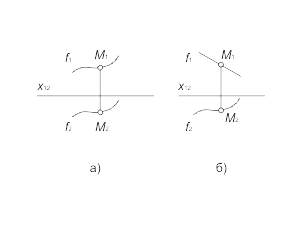
В частном случае, когда плоская кривая принадлежит проецирующей плоскости, она моделируется прямой и кривой линией (рис. 1.27 б). Построение произвольной точки M, принадлежащей кривой линии f , выполняется по тем же правилам, как и для прямой линий. |
Рис. 1-27 |
|||
|
Рис. 1-28 Рис. 1-29 |
||||
Порядок кривой линии Наибольшее число точек пересечения плоской кривой с прямой линией определяет порядок плоской кривой. Наибольшее число точек пересечения пространственной кривой линии с плоскостью определяет порядок пространственной кривой. Рассмотрим некоторые кривые линии, наиболее широко применяемые на практике. Среди плоских кривых линий особого внимания заслуживают кривые второго порядка в виду их широкого применения в ряде разделов физики, в астрономии, механике, архитектуре и других областях науки и техники. Известно, например, что планеты движутся по эллипсам. Траекториями движения твердого тела могут быть эллипс и парабола. Направленные под углом к горизонту снаряды, неуправляемые баллистические ракеты движутся по параболам. |
||||
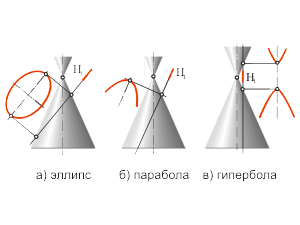
Кривые второго порядка Кривые второго порядка называются коническими сечениями, так как они могут быть получены при пересечении поверхности прямого кругового конуса плоскостью. В зависимости от положения секущей плоскости σ по отношению к образующим конуса получаются различные кривые второго порядка: - эллипс или окружность, когда плоскость пересекает все образующие (эти линии не имеют несобственных точек) (рис. 1.30 а); - парабола, когда секущая плоскость параллельна одной образующей (парабола имеет одну несобственную точку) (рис. 1.30 б); - гипербола, когда плоскость параллельна двум образующим (гипербола имеет две несобственные точки) (рис. 1.30 в); - кривая, распавшаяся на пару прямых, когда плоскость проходит через вершину конуса. При параллельном проецировании проекцией эллипса и окружности является эллипс или, в частном случае, окружность, проекцией параболы является парабола, проекцией гиперболы – гипербола. |
||||
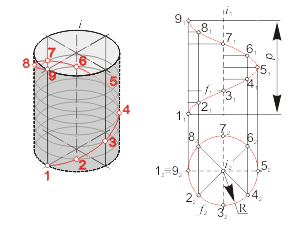
Винтовая линия Алгоритм решения: |
Рис. 1-31
|
|||