Краткое содержание лекции 2
к лекции 1
Моделирование прямой линии
 

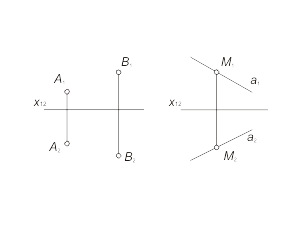
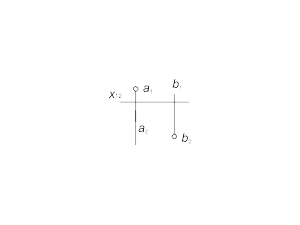
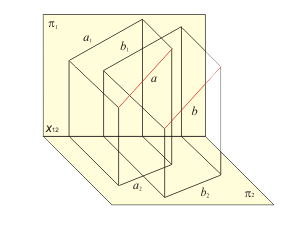
Прямая, в общем случае, моделируется двумя парами точек (рис.1.13 а) или парой прямых (рис. 1.13 б).

Прямую линию, не параллельную и не перпендикулярную плоскостям проекций, будем называть прямой общего положения.

Задача 1.1 Построить модель произвольной точки М, принадлежащей прямой a.

Алгоритм решения:

1. Отметим произвольно на a1 проекцию M1 (рис. 1.13 б).
2. Проведем через нее линию проекционной связи, которая при пересечении с прямой a2 определит вторую проекцию М2 точки М.

Рис 1.13 а,б

Прямые частного положения.

Различают две группы прямых частного положения:

1) Проецирующие прямые

Проецирующие прямые – прямые, проходящие через один из центров проецирования. Одна из проекций проецирующей прямой вырождается в точку (рис. 1.14).

Прямая a – фронтально-проецирующая прямая.

Прямая b – горизонтально-проецирующая прямая.

Рис 1.14
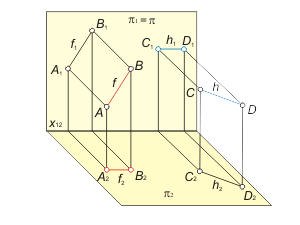
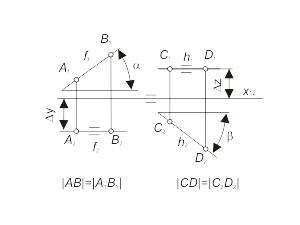
2) Линии уровня

Линии уровня - прямые, параллельные одной из плоскостей проекций.

Прямая f(f1, f2), параллельная плоскости проекций π1, называется фронталью. Вторая проекция фронтали параллельна оси проекций (f2 || x12) (рис. 1.15 а).

Прямая h(h1, h2), параллельная плоскости проекций π2, называется горизонталью. Первая проекция горизонтали параллельна оси проекций (h1 || x12).

Любой отрезок линии уровня (в первом поле для фронтали и во втором поле для горизонтали) проецируется в натуральную величину. Кроме того, первая проекция фронтали f1 и вторая проекция горизонтали h2 определяют углы наклона этих линий к плоскостям проекций π2(α) и π1 (β) соответственно, а ∆y и ∆z определяют расстояния от прямых f и h до плоскостей проекций: ∆y = | f , π1|, ∆z = | h, π2 | (рис. 1.15 б)..

Рис 1.15 а

Рис 1.15 б

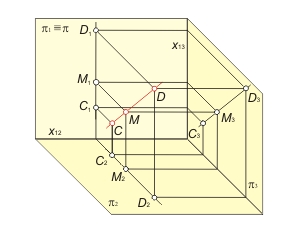
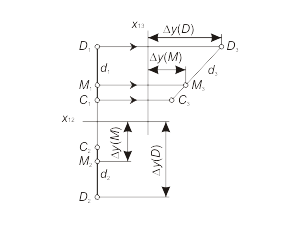
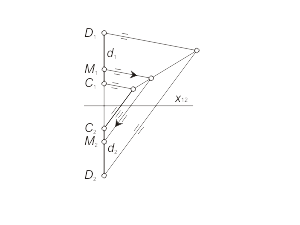
Прямая d, параллельная плоскости проекций π3 (π1 ⊥ π3 ⊥ π2), называется профильной прямой (рис. 1.16 а).

Обе проекции этой прямой лежат на линии проекционной связи, перпендикулярной x12. Наличие проекций двух точек С и D, принадлежащих этой прямой, делают ее модель однозначной. Для построения произвольной точки M, принадлежащей профильной прямой d, можно воспользоваться проекцией прямой на плоскость π3 (рис. 1.16 б) или пятым свойством параллельного проецирования – свойством пропорциональности (рис. 1.16 в).

Рис 1.16 а

Рис 1.16 б

Рис 1.16 в
 
Взаимное положение прямых
 
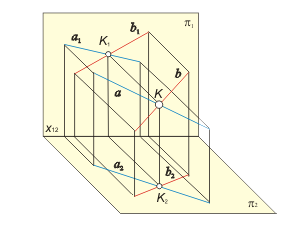
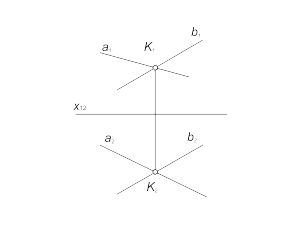
Пересекающиеся прямые

Проекции пересекающихся между собой прямых пересекаются в точке, которая является проекцией точки пересечения этих прямых (рис. 1.17).

Рис 1.17 а

Рис 1.17 б
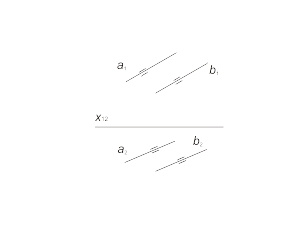
Параллельные прямые

Проекции параллельных прямых параллельны между собой (рис. 1.18).

Рис 1.18 а

Рис 1.18 б
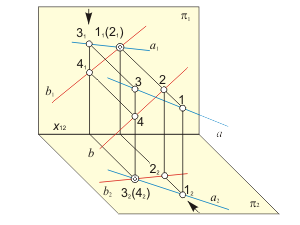
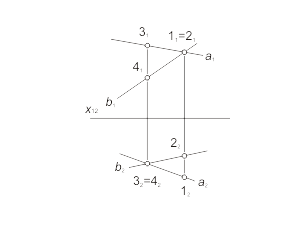
Скрещивающиеся прямые

Проекции скрещивающихся между собой прямых пересекаются в точке, которая является проекцией конкурирующих точек, принадлежащих этим прямым (рис. 1.19).

На основании расположения горизонтальных проекций 12 и 22 конкурирующих точек 1 и 2 можно сделать вывод, что прямая b находится за прямой a, а на основании расположения фронтальных проекций 31 и 41 конкурирующих точек 3 и 4 можно сделать вывод, что прямая b находится под прямой a.

Рис 1.19 а

Рис 1.19 б