|
||||||||||||||||
 |
||||||||||||||||
В начертательной геометрии для образования поверхностей преимущественно используют кинематический и каркасный способы. Кинематический способ Поверхность рассматривается как совокупность всех последовательных положений некоторой линии – образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей. Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих. Каркасный способ Поверхность рассматривается как совокупность некоторого числа линий, образующих каркас. Основное отличие каркасных поверхностей от кинематических состоит в том, что для первых задается определенное число линий каркаса – дискретный каркас, а у вторых в любой точке поверхности может быть построена линия каркаса, т.е. поверхность имеет непрерывный каркас. При моделировании поверхности важную роль играет ее определитель. Определитель поверхности Совокупность условий, задающих поверхность, называется определителем поверхности. Определитель состоит из двух частей: геометрической и алгоритмической. Геометрическая часть определителя включает в себя геометрические элементы, участвующие в образовании поверхности. Такой набор элементов называется репером (от французского слова repere – метка, ориентир). Алгоритмическая часть определителя содержит перечень операций, позволяющих реализовать переход от репера к остальным точкам поверхности. При моделировании поверхности необходимо: 1. Промоделировать репер. 2. Реализовать алгоритм, посредством которого осуществляется переход от модели репера к модели произвольной точки, принадлежащей данной поверхности. На эпюре Монжа поверхность задается проекциями ее репера. Построение произвольной точки, принадлежащей поверхности, осуществляется с помощью простейших линий каркаса поверхности, проходящих через эту точку. |
|
|||||||||||||||
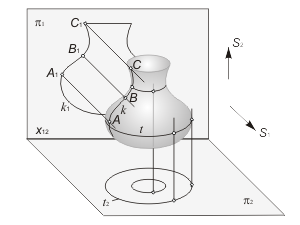
При моделировании поверхности возникает понятие очерка поверхности. Совокупность точек касания проецирующих прямых поверхности образует контурную линию – k (рис. 1.32). Очерк – проекция k1 контурной линии на плоскость проекций. Контурная линия делит поверхность на две части – видимую и невидимую. |
Рис. 1.32 |
|||||||||||||||
Все поверхности можно разделить на два класса: линейчатые поверхности и нелинейчатые поверхности. В каждом классе поверхностей можно выделить подклассы: поверхности вращения, поверхности параллельного переноса, винтовые поверхности и др. |
||||||||||||||||
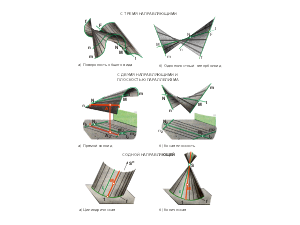
Линейчатая поверхность образуется движением прямой линии (образующей), которая, в общем случае, пересекает три направляющие, в частном случае, - две или одну направляющую (рис. 1.33). Линейчатые поверхности с одной направляющей Линейчатые поверхности с одной направляющей образуются движением прямой линии, которая пересекает направляющую (кривую или ломаную линию) и вершину (собственную или несобственную точку). В таблице 1 представлены различные формы поверхности с одной направляющей в зависимости от вида направляющей и вершины. |
Рис. 1.33 |
|||||||||||||||
Таблицa 1
|
||||||||||||||||
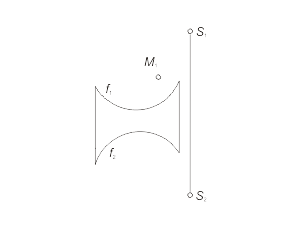
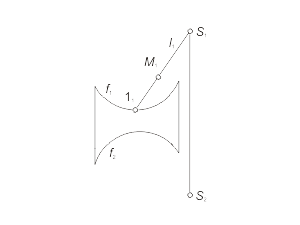
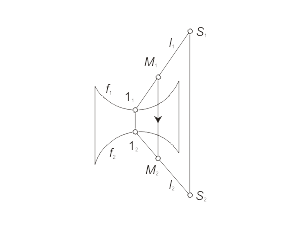
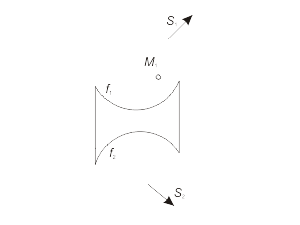
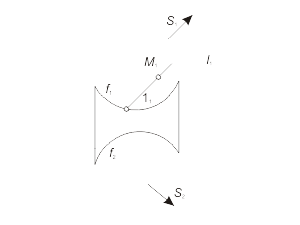
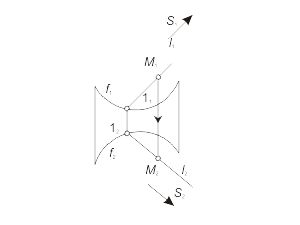
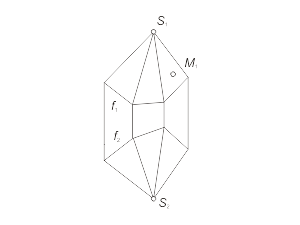
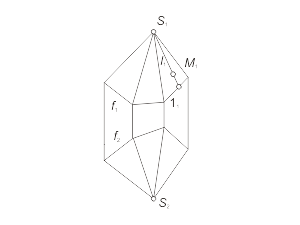
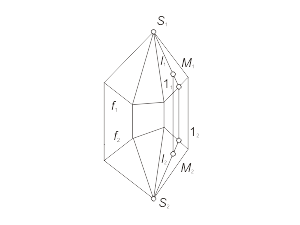
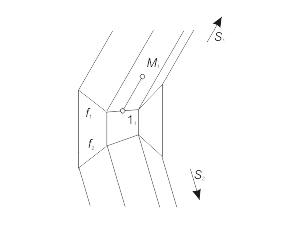
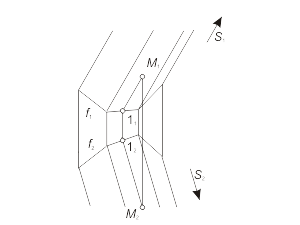
Для построения модели конической поверхности необходимо задать на эпюре Монжа проекции ее репера - направляющей (кривая линия) и вершины (собственная точка), а также решить задачу построения произвольной точки поверхности. Задача 1.4 Построить произвольную точку M, принадлежащую конической поверхности Φ(f, S) (рис. 1.34 а, б, в). Алгоритм решения 1. Отмечаем произвольно проекцию M1 точки M (рис. 1.34 а). 2. Через S1 и M1 проводим проекцию l1 образующей l, принадлежащей поверхности Φ (рис. 1.34 б). 3. Отмечаем проекцию 11 точки пересечения образующей l с направляющей f. 4. Находим проекцию 12 из условия принадлежности точки 1 линии f. 5. Строим вторую проекция l2, соединяя точки S2 и 12 (рис. 1.34 в). 6. Через точку M1 проводим линию проекционной связи и при пересечении ее с прямой l2 отмечаем искомую проекцию M2 точки M, принадлежащей образующей l, а следовательно, и поверхности Φ. |
||||||||||||||||
Для построения модели цилиндрической поверхности необходимо задать на эпюре Монжа проекции ее репера - направляющей f (кривая линия) и вершины S (несобственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки цилиндрической поверхности будет решаться аналогично задаче на принадлежность точки конической поверхности (рис. 1.35 а, б, в). |
||||||||||||||||
Для построения модели пирамидальной поверхности необходимо задать на эпюре Монжа проекции ее репера - направляющей f (ломаная линия) и вершины S (собственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки пирамидальной поверхности будет решаться аналогично задаче на принадлежность точки конической поверхности (рис. 1.36 а, б, в). |
||||||||||||||||
Для построения модели призматической поверхности необходимо задать на эпюре Монжа проекции ее репера - направляющей f (ломаная линия) и вершины S (несобственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки призматической поверхности будет решаться аналогично задаче на принадлежность точки цилиндрической поверхности (рис. 1.37 а, б, в). Следует отметить, что, умея строить одну точку поверхности, можно построить проекции любой линии, принадлежащей заданной поверхности, рассматривая эту линию, как совокупность отдельных точек . |
||||||||||||||||
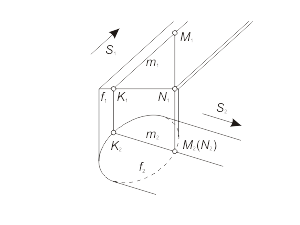
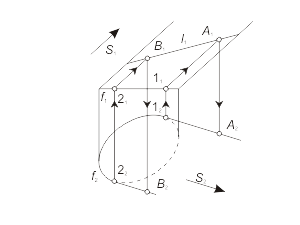
Пример. Построение линии l, принадлежащей цилиндрической поверхности Φ(f, S) - рис. 1.38 а. Порядок построения: 1. Построение очерковых линий и определение видимости направляющей f (рис. 1.38 б). Для определения видимости линии f используются конкурирующие точки M и N . На основании расположения фронтальных проекций этих точек можно сделать вывод, что точка N, принадлежащая направляющей f, находится под точкой M, принадлежащей образующей m. Следовательно, участок линии f, содержащий точку N при проецировании на плоскость π2, будет невидимым. На проекции f2 этот участок отмечен штриховой линией. 2. Определение проекций точек изменения видимости линии l при проецировании на плоскость π2(рис. 1.38 в). Проекция l1 проведена произвольно. Построение начинается с горизонтальной проекции – с точек касания (12 и 22) очерковых прямых к кривой f2. Стрелками показана последовательность действий определения искомых проекций A2 и B2 . |
||||||||||||||||
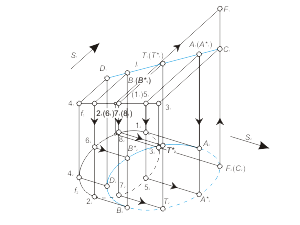
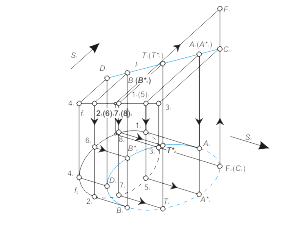
3. Построение точек С и D (рис. 1.39 а). Построение начинается с фронтальных проекций C1 и D1. Проекции C2 и D2 определяются по алгоритму решения задачи 1.4. 4. Построение точек A*, B*, T и T* (рис. 1.39 б). Построение начинается с фронтальной проекции: точка T1(T1*) отмечается произвольно на l1, проекция T2 (T2*) определяется по алгоритму решения задачи 1.4. Аналогично строятся остальные точки заданной линии. 5. Определение видимости линии l. Видимость линии l определяется по конкурирующим точкам C и F цилиндрической поверхности. На основании расположения фронтальных проекций этих точек можно сделать вывод, что точка F выше точки C. Следовательно, часть линии l, содержащая точку C, будет невидимой от точки A до точки B. Линейчатые поверхности с двумя направляющими и плоскостью параллелизма. Такие поверхности образуются движением прямой, которая движется параллельно некоторой плоскости α и пересекает при этом две направляющие m и n. |
Рис. 1.39 а |
|||||||||||||||
В таблице 2 представлены различные формы поверхности с двумя направляющими в зависимости от вида направляющих. Таблица 2
|
||||||||||||||||
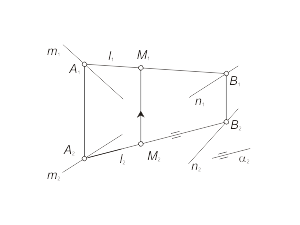
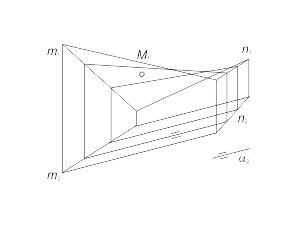
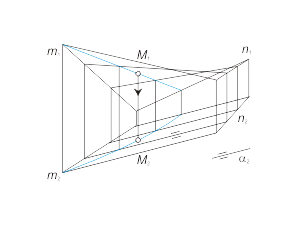
Широкое применение в инженерной практике находит косая плоскость. Иначе косая плоскость называется гиперболическим параболоидом, так как ее каркас состоит не только из прямых линий, но также из семейств кривых второго порядка - гипербол и парабол. Моделирование косой плоскости. Для построения модели косой плоскости необходимо задать на эпюре Монжа проекции направляющих m и n, а также проекции плоскости параллелизма α и решить задачу построения произвольной точки поверхности. Задача Построить недостающую проекцию M1 точки M, принадлежащей косой плоскости Φ(m, n, α). Проекция M2 выбрана произвольно. Для простоты решения задачи в качестве плоскости параллелизма возьмем горизонтально-проецирующую плоскость. |
||||||||||||||||
Алгоритм решения 1. Через M2 параллельно α2 проводим горизонтальную проекцию l2 образующей l, принадлежащей поверхности Φ (рис. 1.40 а), 2. Строим фронтальную проекцию l1, используя для построения точки пересечения A и B образующей l с направляющими m и n. 3. Через точку M2 проводим линию проекционной связи и при пересечении ее с прямой l1 отмечаем искомую проекцию M1 точки M, принадлежащей образующей l, а, следовательно, и поверхности Φ. На рисунке 1.40 б) и в) показано построение недостающей проекции M2 точки M, принадлежащей косой плоскости. Проекция M1 выбирается произвольно (рис. 1.40 б). Далее строятся проекции линий каркаса поверхности аналогично построению проекций прямой l (рис. 1.40 а). Через M1 проводится произвольно проекция k1 кривой k, принадлежащей поверхности Φ. При построении k2 используются точки пересечения линии k с линиями каркаса. Искомая проекция M2 определяется на пересечении линии проекционной связи с горизонтальной проекцией линии k. |
||||||||||||||||
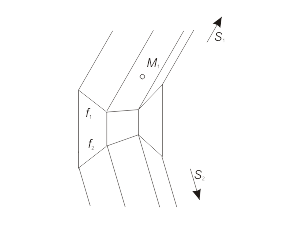
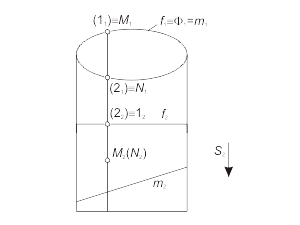
Цилиндрическая и призматическая поверхности могут занимать проецирующее положение в том случае, если направление на вершину (несобственную точку) будет совпадать с направлением проецирования на одну из плоскостей проекций. Другими словами, образующие проецирующей поверхности будут перпендикулярны одной из плоскостей проекций. Пример 1: Фронтально-проецирующая цилиндрическая поверхность. |
||||||||||||||||
Фронтальная проекция любой точки, принадлежащей поверхности Φ(f, S) будет находиться на вырожденной проекции Φ1, которая совпадает с проекцией f1 направляющей линии f. На рис. 1.41 показано положение проекций точек M, N и линии m, принадлежащих цилиндрической поверхности. |
||||||||||||||||
Пример 2: Горизонтально-проецирующая призматическая поверхность . |
||||||||||||||||
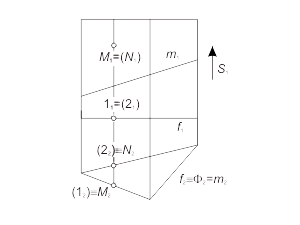
Горизонтальная проекция любой точки, принадлежащей поверхности Φ(f, S) будет находиться на вырожденной проекции Φ2, которая совпадает с проекцией f2 направляющей линии f. На рис. 1.42 показано положение проекций точек M, N и линии m, принадлежащих призматической поверхности. |
Рис. 1.42 |
|||||||||||||||