|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
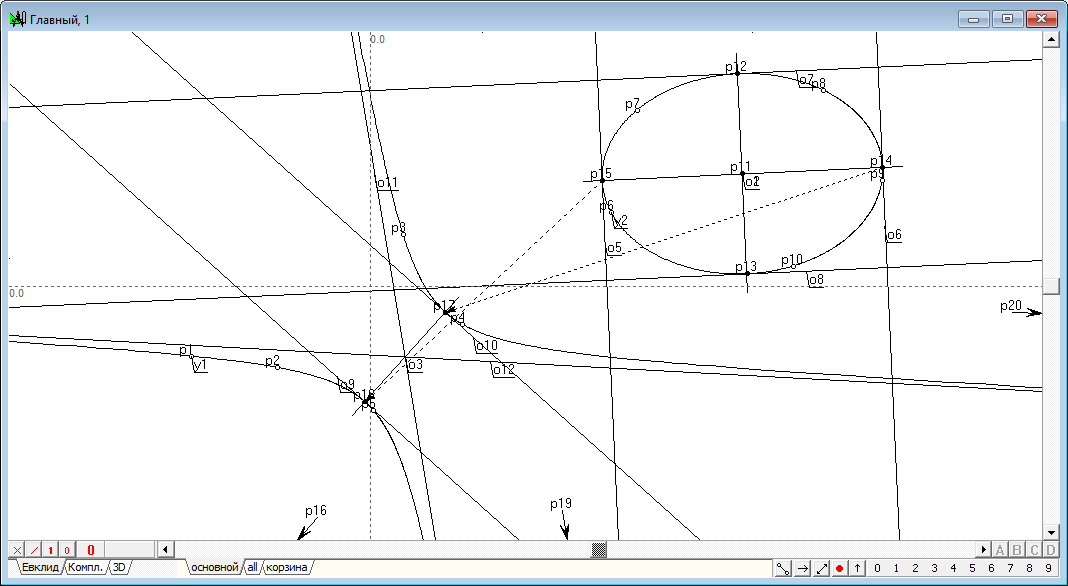
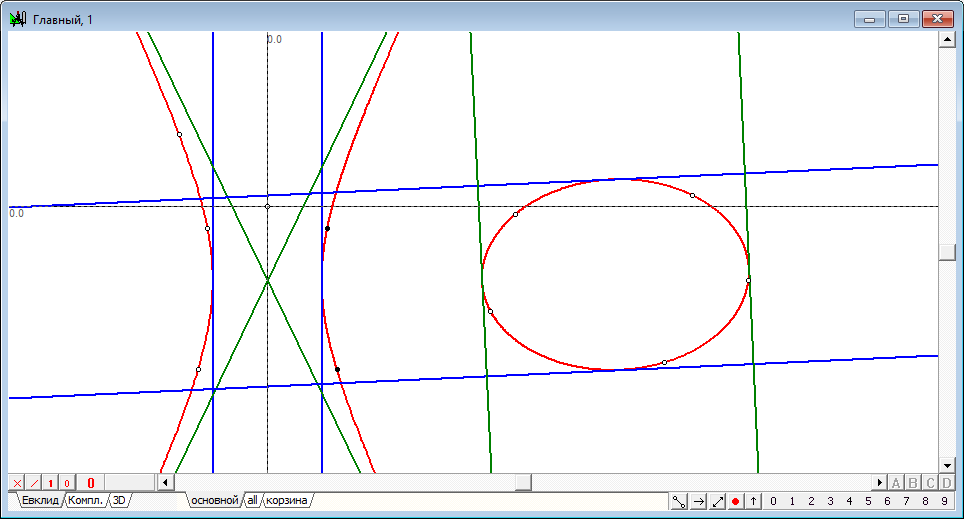
Отношение предназначено для построения прямых линий, являющихся касательными к конике в точках ее пересечения с главными диаметрами. С точки зрения обычной математики асимптотой называется прямая линия, бесконечно близко приближающаяся к данной кривой, но не пересекающаяся с ней. В проективной геометрии асимтота касается кривой в бесконечно удаленной точке. Функциональная равнозначностьглавных диаметров коник позволяет считать асимптотами прямые линии, касающиеся коники в точках ее пересечения с диаметрами. Это допущение подтверждается конструктивной схемой построения данных прямых. |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
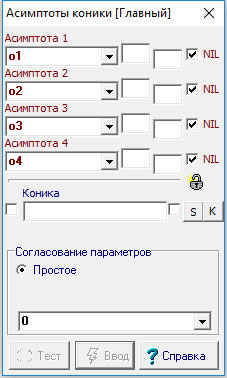
Прототип команды: YA Согласование Асимптота1 Асимптота2 Асимптота3 Асимптота4; Коника . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Геометрическая схема реализации функции | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пояснения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Между заранее заданным эллипсом и произвольной коникой устанавливается коллинеация посредством расстановки в пары точек, полученных от пересечения главных диаметров эллипса и главных диаметров вводимой коники. Строятся касательные в точках на эллипсе, после чего все они переводятся в сформированной коллинеации. Вне зависимости от того, какого вида была исходная кривая - эллипсом или гиперболой, задача по построению необходимых прямых будет решена. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1: Построить асимптоты к двум коникам: эллипсу и гиперболе.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||