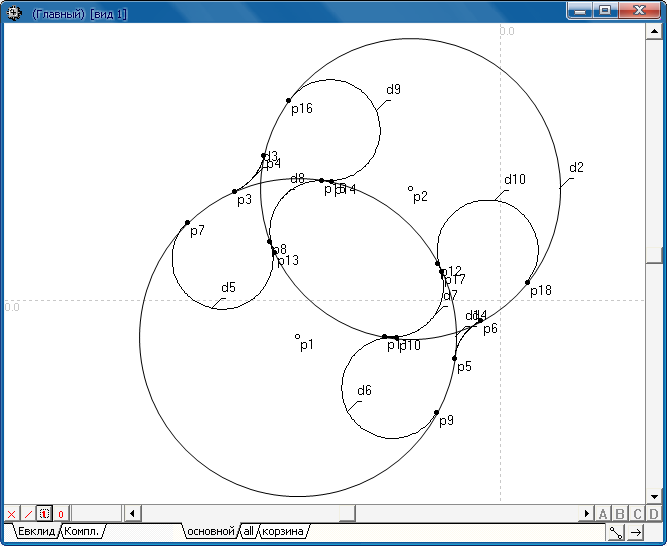
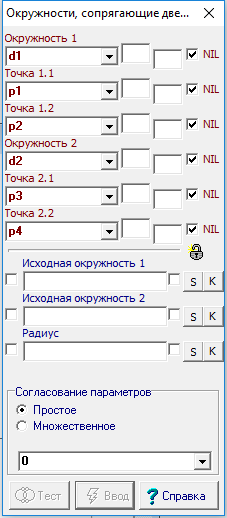
Отношение предназначено для выполнения сопряжения двух Исходных окружностей двумя Сопрягающими окружностями, а также построения Точек касания объектов, участвующих в операции.

В данном отношении сопрягающие окружности считаются ориентированными в направлении против часовой стрелки при положительном значении радиуса и в противоположную сторону – при отрицательном.

Радиус является вещественной величиной и может быть как положительным, так и отрицательным.

При нулевом радиусе сопряжения операция не определена.

Первая сопрягающая окружность касается первой исходной окружности в первой точке касания 1.1 и второй исходной окружности в точке 1.2. Вторая сопрягающая окружность касается первой исходной окружности в первой точке касания 2.1 и второй исходной окружности в точке 2.2.

Предопределенный стиль линии сопрягающих окружностей – ограниченная линия (дуга). Первая сопрягающая дуга имеет в качестве начальной точки точку 1.1, а в качестве конечной – 1.2. Вторая сопрягающая дуга имеет в качестве начальной точки точку 2.2, а в качестве конечной – 2.1.

Стиль линий окружностей, принятый по умолчанию, можно изменять, устанавливая соответствующие атрибуты объектов. Первая сопрягающая окружность при касании располагается таким образом, что ее точка центра находится по левую сторону от условного вектора, соединяющего центр первой исходной окружности со второй исходной окружностью.

Центр второй сопрягающей окружности находится по правую сторону от этого вектора. Будем называть касание окружностей внешним, если при касании одна окружность (исходная или сопрягающая) не находится во внутренней области другой. Касание, при котором одна из окружностей находится во внутренней области другой окружности, будем называть внутренним.

При положительном радиусе исходной окружности будут соблюдаться следующие правила сопряжения: если перед именем списочной переменной исходной окружности стоит знак “минус”, то касание этих окружностей будет внутренним. При отсутствии знака “минус” касание – внешнее.

При отрицательном знаке исходной окружности это правило становится обратным. Возможность построения сопрягающих окружностей зависит от соотношений радиусов всех окружностей, участвующих в операции.

Если в процессе расчета обнаруживается, что при заданных значениях входных параметров реализовать сопряжение невозможно, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.

Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.

Пример:

Построить сопряжения окружностей d1 и d2 окружностями (дугами). Радиусы и способы расположения сопрягающих окружностей по отношению к исходным объектам представлены в протоколе.

Алгоритм "Главный"

1 Точка p1 задана координатами -120.5 и -21.5 . 2 Окружность d1 задана центром p1 и радиусом 94.2 . 3 Точка p2 задана координатами -53.5 и 66.5 . 4 Окружность d2 задана центром p2 и радиусом 89.05 . 5 Окружности d3 и d4 радиуса 30 касаются окружностей d1 и d2 в точках p3 и p4 , p5 и p6 . 6 Окружности d5 и d6 радиуса 30 касаются окружностей -d1 и d2 в точках p7 и p8 , p9 и p10 . 7 Окружности d7 и d8 радиуса 30 касаются окружностей -d2 и -d1 в точках p11 и p12 , p13 и p14 . 8 Окружности d9 и d10 радиуса 30 касаются окружностей d1 и -d2 в точках p15 и p16 , p17 и p18 .