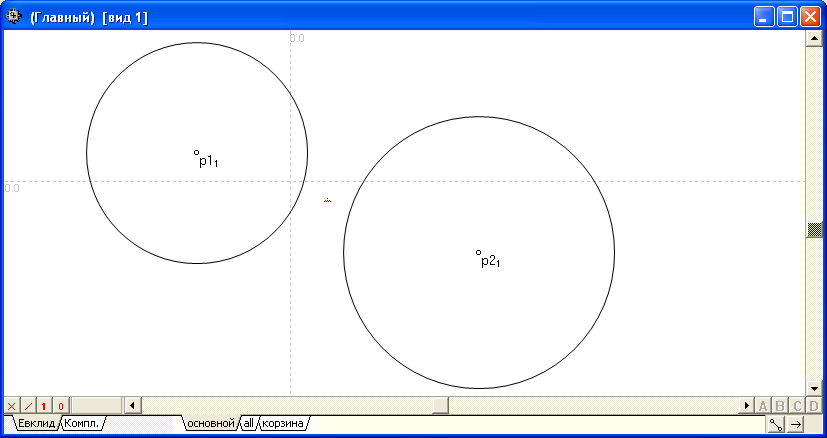
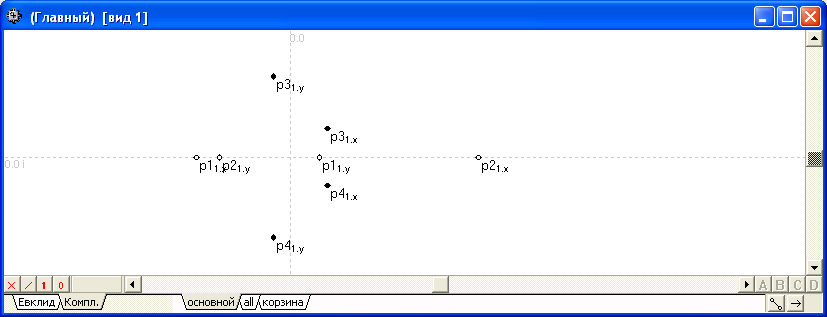
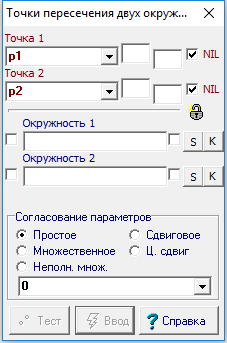
Точки пересечения двух окружностей
 

Отношение предназначено для присвоения двум объектам типа точка Точка 1 и Точка 2 значений, определяющих точки как геометрические места точек пересечения двух окружностей Окружность 1 и Окружность 2.

Точка 1 образуется слева по отношению к направлению воображаемой линии, соединяющей центр первой окружности с центром второй.

Точка 2 образуется справа по отношению к направлению воображаемой линии, соединяющей центр первой окружности с центром второй.

Относительное положение двух окружностей может быть таким, что они не определяют вещественных точек пересечения. В таком случае образуются комплексные точки пересечения окружностей – они могут быть отображены в окне реализации алгоритма при переключении на закладку отображения комплекснозначных объектов Компл.

Если стиль линии исходных объектов таков, что точка не попадает во внутреннюю область хотя бы одной исходной линии, то такая точка будет интерпретирована, как NIL-объект.

Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.
 
 
 
Клавиша
Предварительно
выделено:
Действие
Выделение после действия:
p, P Две окружности Нахождение точек пересечения двух окружностей Выделяются точки пересечения,
выделение исходных объектов снимается
 
 
Параметры
Типы объектов
Функциональное назначение параметров
Точка 1
Точка
Первая точка пересечения окружностей
Точка 2
Точка
Вторая точка пересечения окружностей
Окружность 1
Окружность
Первая исходная окружность
Окружность 2
Окружность
Вторая исходная окружность
 

Прототип команды: P3 Согласование Точка1 Точка2 ; Окружность1 Окружность2 .

 

Пример 1:

Построить точки пересечения окружностей d1 и d2.

Алгоритм "Главный"
1
Точка p1 задана координатами -66.5 и 20.5 .
2
Окружность d1 задана центром p1 и радиусом 77.9 .
3
Точка p2 задана координатами 49.5 и -9.5 .
4
Окружность d2 задана центром p2 и радиусом 95.6 .
5
Точки p3 и p4 есть пересечение окружностей d1 и d2 .

пример1

 

Пример 2:

Построить точки пересечения окружностей d1 и d2 (с учетом комплекснозначных решений).

Алгоритм "Главный"
1
Точка p1 задана координатами -66.5 и 20.5 .
2
Окружность d1 задана центром p1 и радиусом 77.9 .
3
Точка p2 задана координатами 133 и -50 .
4
Окружность d2 задана центром p2 и радиусом 95.6 .
5
Точки p3 и p4 есть пересечение окружностей d1 и d2 .

 

 

 

function CalcP3(X,Y)
{
     var Xc1,Yc1,Xc2,Yc2,R1,R2,Dx,Dy;
     var Xb,Yb,Xe,Ye,Z,Xt,Yt,ZZ,Dummy;
     var Temp1,Temp2;
     var P= {X1:undefined,Y1:undefined,X2:undefined,Y2:undefined}
     var X1= {X:undefined,Y:undefined}
     var Y1= {X:undefined,Y:undefined}
     var X2= {X:undefined,Y:undefined}
     var Y2= {X:undefined,Y:undefined}

//     alert("CalcP3")

     Prizn=false;
     //          X1=undefined;
     //     X2=undefined;
     //     Y1=undefined;
     //     Y2=undefined;
     Xc1=X.Xc;
     Yc1=X.Yc;
     R1=X.R;
     Xc2=Y.Xc;
     Yc2=Y.Yc;
     R2=Y.R;
     Z=Sqr(Xc1.Re)-Sqr(Xc2.Re)+Sqr(Yc1.Re)-Sqr(Yc2.Re)-Sqr(R1.Re)+Sqr(R2.Re);
     Dx=CompSub(Xc2,Xc1);
     Dy=CompSub(Yc1,Yc2);
     if ((Math.abs(Dx.Re)<Eps) && (Math.abs(Dy.Re)<Eps) && (Math.abs(Dx.Im)<Eps) && (Math.abs(Dy.Im)<Eps)) 
     {
          Prizn=true;
          return;
     }

     P=ComDuga1(Xc1,Yc1,Xc2,Yc2,R1,R2);
     X1=P.X1;
     Y1=P.Y1;
     X2=P.X2;
     Y2=P.Y2;

     //          P=LinLin(X1.Re,Y1.Re,X2.Re,Y2.Re,Xc1.Re,Yc1.Re,Xc2.Re,Yc2.Re);
     Dummy=X.Xc.Re*(Y.Yc.Re-Y1.Re)+Y.Xc.Re*(Y1.Re-X.Yc.Re)+X1.Re*(X.Yc.Re-Y.Yc.Re);

     if (CMPOut==false) if (Dummy <= 0) 
     {
          Temp1=X1; Temp2=Y1;
          X1=X2; Y1=Y2;
          X2=Temp1; Y2=Temp2;
     }
     if (CMPOut) { Def1=true; Def2=true; return P }
//          if (X.PointBelongs(X1.Re,Y1.Re) && Y.PointBelongs(X1.Re,Y1.Re)) {Def1=true} else {Def1=false}
//          if (X.PointBelongs(X2.Re,Y2.Re) && Y.PointBelongs(X2.Re,Y2.Re)) {Def2=true} else {Def2=false}
     return P;
} // CalcP3