Окружности Мальфатти

Отношение предназначено для построения окружностей Мальфатти, индуцированных заданным треугольником.

Если тип объекта, указанного в любом из входных параметров, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.

Параметры	Типы объектов	Функциональное назначение параметров
Окружность 1	Окружность	Первая окружность Мальфатти
Окружность 2	Окружность	Вторая окружность Мальфатти
Окружность 3	Окружность	Третья окружность Мальфатти
Первая сторона треугольника	Прямая	Первая сторона исходного треугольника
Вторая сторона треугольника	Прямая	Вторая сторона исходного треугольника
Третья сторона треугольника	Прямая	Третья сторона исходного треугольника

Прототип команды: TR015 Согласование Окружность_1 Окружность_2 Окружность_3 ; Первая_сторона_треугольника Вторая_сторона_треугольника Третья_сторона_треугольника .

Пример: Поcтроить окружности Мальфатти для треугольника, заданного точками p1, p2 и p3.

1		Точка p1 задана координатами -257 и -65.5 .
2		Точка p2 задана координатами -23 и 177.5 .
3		Точка p3 задана координатами 193 и -12.5 .
4		Прямая o1 задана точками p1 и p2 .
5		Прямая o2 задана точками p2 и p3 .
6		Прямая o3 задана точками p3 и p1 .
7		Окружности Мальфатти d1 , d2 , d3 для треугольника, построенного на прямых o1 , o2 , o3 .

Структура Алгоритма

Алгоритм "Главный"

1		Точка p1 есть пересечение прямых o19 и o20 .
2		Точка p2 есть пересечение прямых o19 и o18 .
3		Точка p3 есть пересечение прямых o18 и o20 .
4		Прямая o1 задана точками p1 и p2 .
5		Прямая o2 задана точками p2 и p3 .
6		Прямая o3 задана точками p3 и p1 .
7		Бисcектрисы o4 и o5 в угле, образованном прямыми o1 и o2 .
8		Бисcектрисы o6 и o7 в угле, образованном прямыми o2 и o3 .
9		Бисcектрисы o8 и o9 в угле, образованном прямыми o3 и o1 .
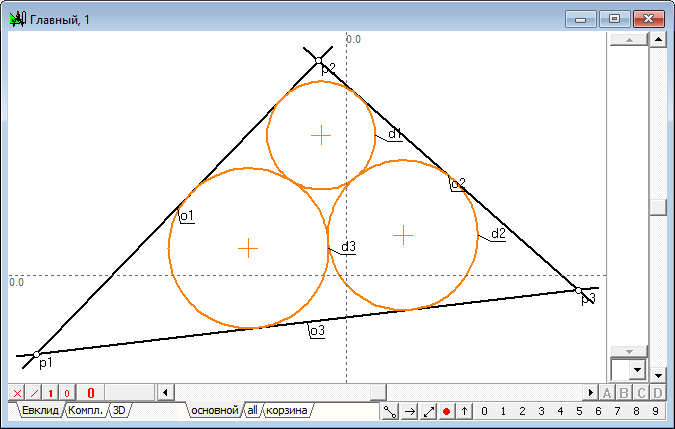
10		Вписанная окружность d1 , касается треугольника, построенного на прямых o1 , o5 , o9 , в точках p4 , p5 , p6 .
11		Вписанная окружность d2 , касается треугольника, построенного на прямых o5 , o2 , o7 , в точках p7 , p8 , p9 .
12		Вписанная окружность d3 , касается треугольника, построенного на прямых o3 , o9 , o7 , в точках p10 , p11 , p12 .
13		Прямая o12 касается окружностей -d3 и d1 в точках p17 и p18 .
14		Прямая o13 касается окружностей d1 и -d3 в точках p19 и p20 .
15		x2:31@lv=1@red=255@green=128 o9 o13 o12
16		Прямая o14 касается окружностей -d3 и d2 в точках p21 и p22 .
17		Прямая o15 касается окружностей d2 и -d3 в точках p23 и p24 .
18		x3:38@lv=1@red=255@green=128 o7 o14 o15
19		Бисcектрисы o35 и o36 в угле, образованном прямыми x3 и o1 .
20		Бисcектрисы o37 и o38 в угле, образованном прямыми x2 и o2 .
21		Точка p42 есть пересечение прямых o9 и o35 .
22		Точка p43 есть пересечение прямых o5 и o36 .
23		Точка p44 есть пересечение прямых o37 и o7 .
24		Точка p45 есть проекция точки p44 на прямую o2 .
25		Окружность d12 задана центром p44 и точкой p45 .
26		Точка p46 есть проекция точки p42 на прямую o3 .
27		Окружность d13 задана центром p42 и точкой p46 .
28		Точка p47 есть проекция точки p43 на прямую o2 .
29		Окружность d14 задана центром p43 и точкой p47 .
30		Прямая o18 задана координатами двух точек: X1= -346.02196 , Y1= -60.845118 , X2= -247.8381 , Y2= 98.388961 .
31		Прямая o19 задана координатами двух точек: X1= -281.19543 , Y1= 180.83823 , X2= -140.84287 , Y2= 50.555799 .
32		Прямая o20 задана координатами двух точек: X1= -79.163263 , Y1= 46.150113 , X2= -360.49778 , Y2= -22.452711 .