Окружность, вписанная в треугольник

Отношение предназначено для выполнения построения окружности, вписанной в треугольник. Одновременно строятся точки касания окружности к сторонам треугольника.

Если тип объекта, указанного во входном параметре, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.

	Клавиша	Предварительно выделено:	Действие	Выделение после действия:
	d	Три прямые	Вписанная в треугольник окружность	Выделяется окружность

Параметры	Типы объектов	Функциональное назначение параметров
Окружность	Окружность	Окуржность, вписанная в треугольник
Точка 1	Точка	Точка касания вписанной окружности к первой стороне треугольника
Точка 2	Точка	Точка касания вписанной окружности ко второй стороне треугольника
Точка 3	Точка	Точка касания вписанной окружности к третьей стороне треугольника
Первая сторона треугольника	Прямая	Первая сторона треугольника
Вторая сторона треугольника	Прямая	Вторая сторона треугольника
Третья сторона треугольника	Прямая	Третья сторона треугольника

Прототип команды: TR006 Согласование Окружность Точка1 Точка2 Точка3 ; Первая_сторона_треугольника Вторая_сторона_треугольника Третья_сторона_треугольника .

Входные параметры: o1, o2, o3.

Выходной параметр:d1.

Алгоритм "Главный"

1		Прямая o1 задана координатами двух точек: X1= -255.5 , Y1= -63 , X2= -167.5 , Y2= 21 .
2		Прямая o2 задана координатами двух точек: X1= -141.5 , Y1= 178 , X2= -21.5 , Y2= 78 .
3		Прямая o3 задана координатами двух точек: X1= 491.5 , Y1= -174 , X2= -291.5 , Y2= -120 .
4		Точка p1 есть пересечение прямых o1 и o2 .
5		Точка p2 есть пересечение прямых o2 и o3 .
6		Точка p3 есть пересечение прямых o3 и o1 .
7		Прямая o4 задана точками p1 и p2 .
8		Прямая o5 задана точками p2 и p3 .
9		Прямая o6 задана точками p3 и p1 .
10		Бисcектрисы o7 и o8 в угле, образованном прямыми o4 и -o5 .
11		Бисcектрисы o9 и o10 в угле, образованном прямыми o5 и -o6 .
12		Точка p4 есть пересечение прямых o7 и o9 .
13		Точка p5 есть проекция точки p4 на прямую o4 .
14		Точка p6 есть проекция точки p4 на прямую o5 .
15		Точка p7 есть проекция точки p4 на прямую o6 .
16		Окружность d1 проведена через точки p5 , p6 и p7 .

Структура функции

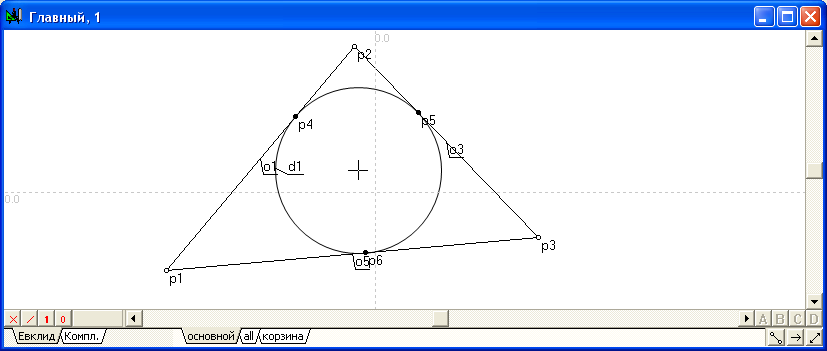
Пример 1:

Построить окружность d1, вписанную в треугольник, заданный вершинами p1, p2 и p3.

Алгоритм "Главный"

1		Точка p1 задана координатами -161.5 и -60 .
2		Точка p2 задана координатами -16.5 и 113 .
3		Точка p3 задана координатами 125.5 и -35 .
4		Прямая o1 задана точками p1 и p2 .
5		Прямая o3 задана точками p2 и p3 .
6		Прямая o5 задана точками p3 и p1 .
7		Вписанная окружность d1 , касается треугольника, построенного на прямых o1 , o3 , o5 , в точках p4 , p5 , p6 .