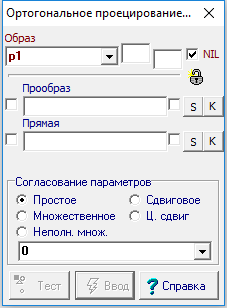
Ортогональное проецирование точки на прямую

Отношение предназначено для присвоения объекту типа точка значения, определяющего Точку как место точки, ортогонально спроецированной из Точки 1 на Прямую.

Точка-проекция будет иметь определенное значение лишь в том случае, если она находится во внутренней области прямой, на которую было выполнено проецирование.

Если точка получила значение, то она добавляется в список инцидентных точек этой прямой.

Внешний вид “инцидентностной” линии может измениться в связи с пополнением этого списка. (Конкретный вид прямой задается атрибутом стиля линии в порождающем ее отношении).

Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.

	Клавиша	Предварительно выделено:	Действие	Выделение после действия:
	p, P	Точки и прямая	Построение ортогональных проекций выделенных точек на выделенную прямую линию	Выделяются точки-проекции, выделение исходных объектов снимается

Параметры	Типы объектов	Функциональное назначение параметров
Образ	Объектный тип	Точка, являющаяся проекцией заданной точки на прямую линию/ Проекция вектора на прямую
Прообраз	Точка, вектор, проективитет	Исходная собственная точка вещественной плоскости / исходный вектор / исходный проективитет в точечном ряде
Прямая	Прямая	Исходная прямая

Прототип команды: PF Согласование Точка ; {-}Объект {-}Прямая .

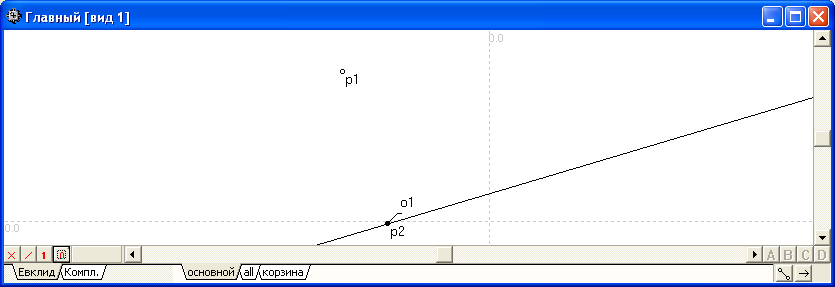
Пример 1:

Спроецировать ортогонально точку на прямую.

Алгоритм "Главный"

1		Прямая o1 задана координатами двух точек: X1= -261 , Y1= -49 , X2= 136 , Y2= 69 .
2		Точка p1 задана координатами -147 и 150 .
3		Точка p2 есть проекция точки p1 на прямую o1 .

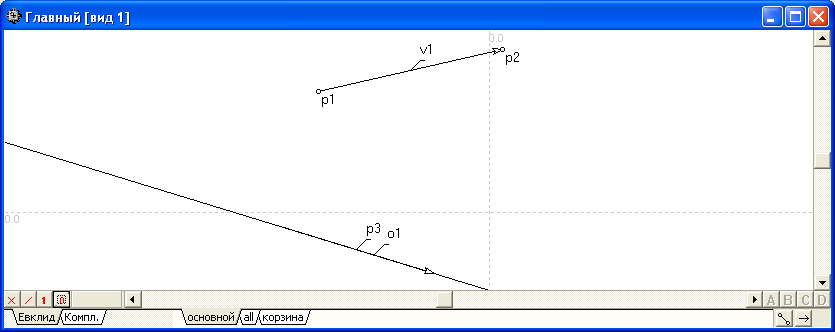
Пример 2:

Найти проекцию вектора на прямую.

Алгоритм "Главный"

1		Прямая o1 задана координатами двух точек: X1= -291 , Y1= 11 , X2= 60 , Y2= -96 .
2		Точка p1 задана координатами -171 и 121 .
3		Точка p2 задана координатами 13 и 163 .
4		Вектор v1 задан точками p1 и p2 .
5		Точка p3 есть проекция точки v1 на прямую o1 .

procedure CalcPF_A(X1,Y1,X2,Y2,XX,YY: complex; var A,B: complex);
var X3,Y3,X4,Y4,Z: complex;
    Dl,Dx,Df,S,C: real;
    LDummy,Prizn: boolean;
begin
     A:=XX;B:=YY;
     SC(X1.Re,Y1.Re,X2.Re,Y2.Re,S,C,Dl,LDummy);
     Fi(0,1,S,C,Df);
     Dx:=Pi/2+Df;
     X3:=CompSum(A,MCompl(200*Cos(Dx),0));
     Y3:=CompSum(B,MCompl(200*Sin(Dx),0));
     X4:=CompSub(A,MCompl(200*Cos(Dx),0));
     Y4:=CompSub(B,MCompl(200*Sin(Dx),0));
     Prizn:=LinLinComp(X1,Y1,X2,Y2,X3,Y3,X4,Y4,A,B,Z);

end; // CalcPF_A

procedure CalcPF(XX,YY: complex; Y: TObj; var A,B: complex);
var X1,Y1,X2,Y2: complex;

begin
     X1:=TOLine(Y).X1;
     Y1:=TOLine(Y).Y1;
     X2:=TOLine(Y).X2;
     Y2:=TOLine(Y).Y2;
     CalcPF_A(X1,Y1,X2,Y2,XX,YY,A,B);
end; // CalcPF

function CalcPF_A(X1,Y1,X2,Y2,XX,YY)
{
     var Dl,Dx,Df,SCDP;
     var LDummy,P;
     var X3,Y3,X4,Y4,Z;
     var AB={A:undefined, B:undefined}

     AB.A=XX; AB.B=YY;
     SCDP=SC(X1.Re,Y1.Re,X2.Re,Y2.Re);
     Df=Fi(0,1,SCDP.S,SCDP.C);
     Dx=Math.PI/2+Df;
     X3=CompSum(AB.A,MCompl(200*Math.cos(Dx),0));
     Y3=CompSum(AB.B,MCompl(200*Math.sin(Dx),0));
     X4=CompSub(AB.A,MCompl(200*Math.cos(Dx),0));
     Y4=CompSub(AB.B,MCompl(200*Math.sin(Dx),0));
     P=LinLinComp(X1,Y1,X2,Y2,X3,Y3,X4,Y4);

     AB.A=P.XX;
     AB.B=P.YY;
     return AB;
} // CalcPF_A

function CalcPF(XX,YY,Y)
{
var X1,Y1,X2,Y2;

     X1=Y.X1;
     Y1=Y.Y1;
     X2=Y.X2;
     Y2=Y.Y2;
     AB=CalcPF_A(X1,Y1,X2,Y2,XX,YY);
     return AB
} // CalcPF