|
| |
Отношение предназначено для построения Контура, отстоящего от заданного контура Контур1 на заданной Дистанции.
Эквидистантный контур может быть построен только для контуров, в состав которых входят отрезки, дуги окружностей и отделенные от иных составляющих контура замкнутые окружности.
Если исходный контур не замкнут, то эквидистантная линия будет построена с отступом на заданную величину Дистанции с обеих сторон от линии исходного контура, а граничные точки исходного контура породят в выходном контуре дуги с радиусом, равным величине Дистанции. Выходной контур будет односвязен и замкнут.
Если исходный Контур замкнут или же состоит из совокупности вложенных друг в друга непересекающихся контуров, то в качестве выходного контура будет построена также совокупность вложенных контуров (или единственный контур, если заданная величина Дистанции на позволяет выполнить построение за счет вырождения формы контуров).
Если внешний контур системы контуров ориентирован по часовой стрелке, то при указании положительной величины Дистанции эквидистантный контур будет строиться внутрь по отношению к составляющим контура с четной степенью вложенности и наружу по отношению к составляющим с нечетной степенью вложенности (при этом понимается, что внешний контур имеет нулевую степень вложенности, так как не вложен в какой-либо другой контур). Отрицательное значение величины Дистанции приведет к противоположному порядку образования эквидистантных линий.
Если внешний контур системы контуров ориентирован против часовой стрелки, то при указании положительной величины Дистанции эквидистантный контур будет строиться наружу по отношению к составляющим контура с четной степенью вложенности и внутрь по отношению к составляющим с нечетной степенью вложенности. Отрицательное значение величины Дистанции приведет к противоположному порядку образования эквидистантных линий.
В любом случае выходной контур строится таким образом, чтобы внений контур с нулевой степенью вложенности был бы ориентирован в направлении, противоположном ходу часовой стрелки.
Если тип объекта, указанного во входном параметре, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NILL-объект.
|
|
| |
| |
| |
Клавиша |
Предварительно
выделено: |
Действие |
Выделение
после
действия: |
 |
w, W |
Контур |
Построение контура, эквидистантного к исходному выделенному контуру, функцией  , очерк которого проходит через точку, соответствующую текущему положению курсора , очерк которого проходит через точку, соответствующую текущему положению курсора |
Выделяется образованный контур |
|
| |
| |
|
Параметры |
Типы объектов |
Функциональное назначение
параметров |
|
Контур |
Контур |
Эквидистантный контур |
|
Контур 1 |
Контур |
Исходный контур |
 |
Дистанция |
Величина |
Величина, определяющая дистанцию между исходным и искомым контуром |
|
| |
Прототип команды: W3 Согласование Контур ; Контур1 {-}Дистанция .
|
| |
Пример 1:
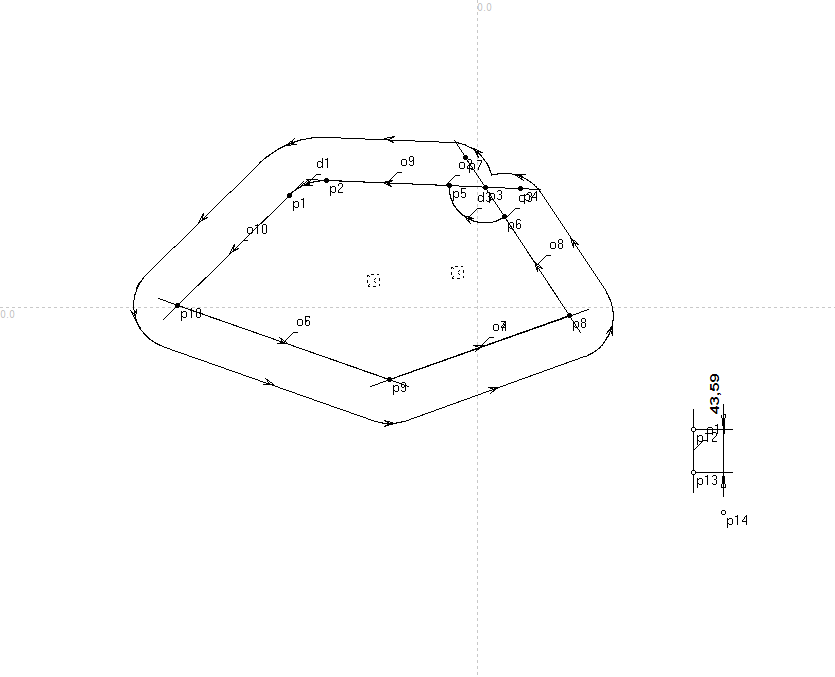
Построить контур w2 на расстоянии f2 от контура w1. Расстояние (с учетом знака) задается регулятором приращения ординат двух точек.
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -300.5 , Y1= -52.5 , X2= -170.5 , Y2= 75.5 . |
2 |
|
Прямая o2 задана координатами двух точек: X1= -248.5 , Y1= 96.5 , X2= 26.5 , Y2= 85.5 . |
3 |
|
Прямая o3 задана координатами двух точек: X1= 5.5 , Y1= 118.5 , X2= 118.5 , Y2= -53.5 . |
4 |
|
Прямая o4 задана координатами двух точек: X1= 167.5 , Y1= -23.5 , X2= -68.5 , Y2= -107.5 . |
5 |
|
Прямая o5 задана координатами двух точек: X1= -2.5 , Y1= -130.5 , X2= -369.5 , Y2= -1.5 . |
6 |
|
Точка p3 есть пересечение прямых o2 и o3 . |
7 |
|
Прямая o11 задана координатами двух точек: X1= 235.5 , Y1= 101.9 , X2= 235.5 , Y2= 1.93 . |
8 |
|
Точка p12 принадлежит объекту o11 с параметром принадлежности 2.5850415 . |
9 |
|
Точка p13 принадлежит объекту o11 с параметром принадлежности 3.0211231 . |
10 |
|
Точка p14 задана относительно точки p13 с приращениями по X 30.5 и Y -39.6 . |
11 |
|
Вертикальная размерная линия приращений f1 на точках p12 , p13 , p14 . |
12 |
|
Окружность d1 радиуса 50 касается прямых -o1 и o2 в точках p1 и p2 . |
13 |
|
Окружность d2 задана центром p3 и радиусом 35.69 . |
14 |
|
Точка p10 есть пересечение прямых o5 и o1 . |
15 |
|
Точки p4 и p5 есть пересечение прямой o2 и окружности d2 . |
16 |
|
Точки p6 и p7 есть пересечение прямой o3 и окружности d2 . |
17 |
|
Точка p8 есть пересечение прямых o3 и o4 . |
18 |
|
Точка p9 есть пересечение прямых o4 и o5 . |
19 |
|
Дуга d3 окружности d2 задана начальной точкой p5 и конечной точкой p6 . |
20 |
|
Прямая o10 задана точками p10 и p1 . |
21 |
|
Прямая o6 задана точками p10 и p9 . |
22 |
|
Прямая o7 задана точками p9 и p8 . |
23 |
|
Прямая o8 задана точками p6 и p8 . |
24 |
|
Прямая o9 задана точками p2 и p5 . |
25 |
|
w1:1@ht=7@grd=255@act=0@chk=0@lay=основной o7,o8,d3,o9,d1,o10,o6 |
26 |
|
Контур w2 на расстоянии f1 от контура w1 . |
|
 у у

|
Пример 2:
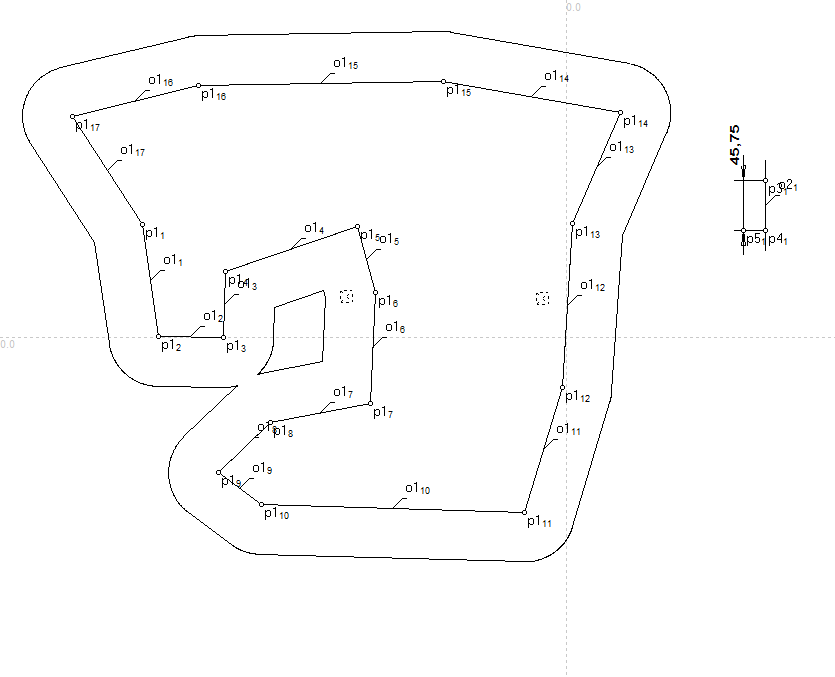
Построить контур p2 на расстоянии f1 от контура w1. Расстояние (с учетом знака) задается регулятором приращения ординат двух точек.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -367.5,-352.5,-292.5,-291.5,-170.5,-153.5,-158.5,-249.5,-297.5,-258.5,-16.5,17.5,27.5,71.5,-91.5,-315.5,-431.5 и 68.5,-34.5,-35.5,25.5,66.5,6.125,-95.5,-113.5,-159.5,-188.5,-195.5,-81.5,69.5,170.5,199.5,195.5,167.5 . |
2 |
|
Прямая o1 задана точками p1 и p1 . |
3 |
|
w1:3@ht=7@grd=255@act=0@chk=0@lay=основной o1 |
4 |
|
Прямая o2 задана координатами двух точек: X1= 204.28 , Y1= 162.88 , X2= 204.28 , Y2= 62.875 . |
5 |
|
Точка p3 принадлежит объекту o2 с параметром принадлежности 0.54258738 . |
6 |
|
Точка p4 принадлежит объекту o2 с параметром принадлежности 1 . |
7 |
|
Точка p5 задана относительно точки p4 с приращениями по X -20 и Y 0 . |
8 |
|
Вертикальная размерная линия приращений f1 на точках p3 , p4 , p5 . |
9 |
|
Контур p2 на расстоянии f1 от контура w1 . |
|

|
Пример 3:
Построить контур w2 на расстоянии f1 от контура w1. Расстояние (с учетом знака) задается регулятором приращения ординат двух точек.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -303.5 и -13.5 . |
2 |
|
Окружность d1 задана центром p1 и радиусом 177.9 . |
3 |
|
Точка p2 задана координатами -362 и 143.2 . |
4 |
|
Окружность d2 задана центром p2 и радиусом 203.2 . |
5 |
|
Точка p3 задана координатами -444.8 и -78.67 . |
6 |
|
Окружность d3 задана центром p3 и радиусом 181.2 . |
7 |
|
Точки p4 и p5 есть пересечение окружностей d2 и d3 . |
8 |
|
Точки p6 и p7 есть пересечение окружностей d1 и d2 . |
9 |
|
Точки p8 и p9 есть пересечение окружностей d1 и d3 . |
10 |
|
Дуга d4 окружности d3 задана начальной точкой p5 и конечной точкой p8 . |
11 |
|
Дуга d5 окружности d3 задана начальной точкой p8 и конечной точкой p4 . |
12 |
|
Дуга d6 окружности d2 задана начальной точкой p6 и конечной точкой p4 . |
13 |
|
Дуга d7 окружности d1 задана начальной точкой p7 и конечной точкой p6 . |
14 |
|
Дуга d8 окружности d2 задана начальной точкой p7 и конечной точкой p5 . |
15 |
|
w1:18@grd=255@blue=255@fsr=192@fsg=192@fsb=192@act=0@chk=0@lay=основной d4,d5,d6,d7,d8 |
16 |
|
Прямая o1 задана координатами двух точек: X1= -70.88 , Y1= 331 , X2= -70.88 , Y2= 231 . |
17 |
|
Точка p10 принадлежит объекту o1 с параметром принадлежности 2.3095315 . |
18 |
|
Точка p11 принадлежит объекту o1 с параметром принадлежности 1.8914324 . |
19 |
|
Точка p12 задана относительно точки p11 с приращениями по X -20 и Y 0 . |
20 |
|
Вертикальная размерная линия приращений f1 на точках p10 , p11 , p12 . |
21 |
|
Точка p13 задана координатами -510.43 и -22.63 . |
22 |
|
Контур w2 на расстоянии f1 от контура w1 . |
|


|
| |
| |
|
| |
|
| |
|
| |
|
 у
у
