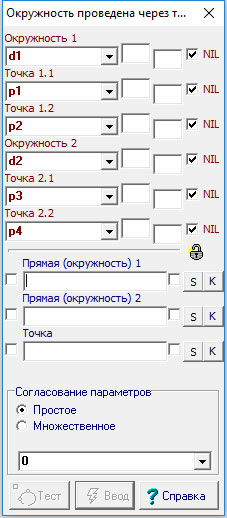
Окружность проведена через точку касательно к двум объектам |
|
| |
Отношение предназначено для построения двух Окружностей, касательных к двум заданным объектам (Прямым или Окружностям), и проходящих через заданную Точку.
Точка, через которую проводятся сопрягающие окружности, должна быть собственной точкой вещественной плоскости.
Если в процессе расчета обнаруживается, что при заданных значениях входных параметров реализовать сопряжение невозможно, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.
Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.
|
|
| |
|
Параметры |
Типы
объектов |
Функциональное назначение
параметров запроса |
|
Окружность 1 |
Окружность |
Первая касательная окружность |
|
Точка 1.1 |
Точка |
Точка касания первой касательной окружности и первого объекта (прямой или окружности) |
|
Точка 1.2 |
Точка |
Точка касания первой касательной окружности и второго объекта (прямой или окружности) |
|
Окружность 2 |
Окружность |
Вторая касательная окружность |
|
Точка 2.1 |
Точка |
Точка касания второй касательной окружности и первого объекта (прямой или окружности) |
|
Точка 2.2 |
Точка |
Точка касания второй касательной окружности и второго объекта (прямой или окружности) |
|
Прямая (окружность) 1 |
Прямая (окружность) |
Первый исходный объект (прямая или окружность) |
|
Прямая (окружность) 2 |
Прямая (окружность) |
Второй исходный объект (прямая или окружность) |
|
Точка |
Точка |
Точка, через которую проведены сопрягающие окружности |
|
| |
Прототип команды: DG Согласование Окружность1 Точка1.1 Точка1.2 Окружность2 Точка2.1 Точка2.2; {-}Прямая(окружность)1 {-}Прямая(окружность)2 Точка .
|
| |
Пояснение к реализации функции:
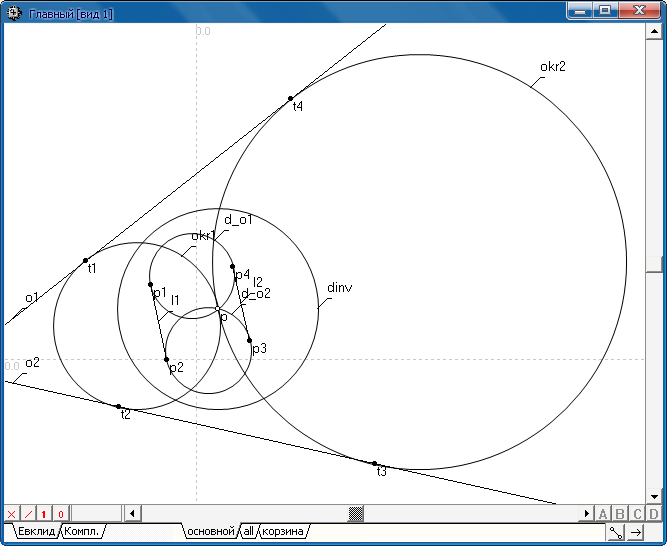
Функция реализована на основе преобразования инверсии. Через точку p проводится произвольная (например радиусом 100) окружность dinv, относительно которой выполняется инверсионное преобразование входных объектов. Объект o1 (прямая или окружность) будет преобразован в окружность okr1. Объект o2 (прямая или окружность) будет преобразован в окружность okr2. Операция сопряжения окружностей okr1 и okr2 прямыми линиями позволяет получить образы l1 и l2 окружностей сопряжения okr1 и okr2 и точек касания в преобразовании инверсии. Прообразы находятся обратным преобразованием l1, l2, p1, p2, p3, p4 относительно окружности инверсии dinv.
Входные параметры: o1, o2 и p.
Выходные параметры: okr1, t1, t2, okr2, t3 и t4.
Алгоритм "Главный" |
1 |
|
Величина chisl есть 100 . |
2 |
|
Прямая o1 задана координатами двух точек: X1= -314.5 , Y1= -60.5 , X2= -55.5 , Y2= 143.5 . |
3 |
|
Прямая o2 задана координатами двух точек: X1= -494.5 , Y1= 45.5 , X2= 124.5 , Y2= -91.5 . |
4 |
|
Точка p задана координатами 20.5 и 51.5 . |
5 |
|
Окружность dinv задана центром p и радиусом chisl . |
6 |
|
Объект d_o1 есть результат инверсного преобразования объекта o1 относительно окружности dinv . |
7 |
|
Объект d_o2 есть результат инверсного преобразования объекта o2 относительно окружности dinv . |
8 |
|
Прямая l1 касается окружностей -d_o1 и d_o2 в точках p1 и p2 . |
9 |
|
Прямая l2 касается окружностей d_o2 и -d_o1 в точках p3 и p4 . |
10 |
|
Объект t1 есть результат инверсного преобразования объекта p1 относительно окружности dinv . |
11 |
|
Объект t2 есть результат инверсного преобразования объекта p2 относительно окружности dinv . |
12 |
|
Объект t3 есть результат инверсного преобразования объекта p3 относительно окружности dinv . |
13 |
|
Объект t4 есть результат инверсного преобразования объекта p4 относительно окружности dinv . |
14 |
|
Объект okr1 есть результат инверсного преобразования объекта l1 относительно окружности dinv . |
15 |
|
Объект okr2 есть результат инверсного преобразования объекта l2 относительно окружности dinv . |
|
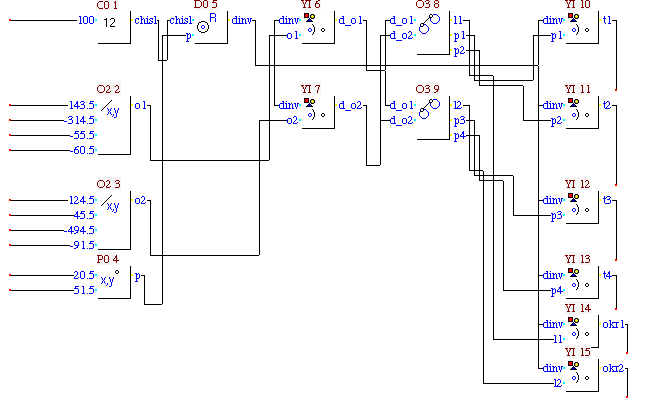
структура функции

|
| |
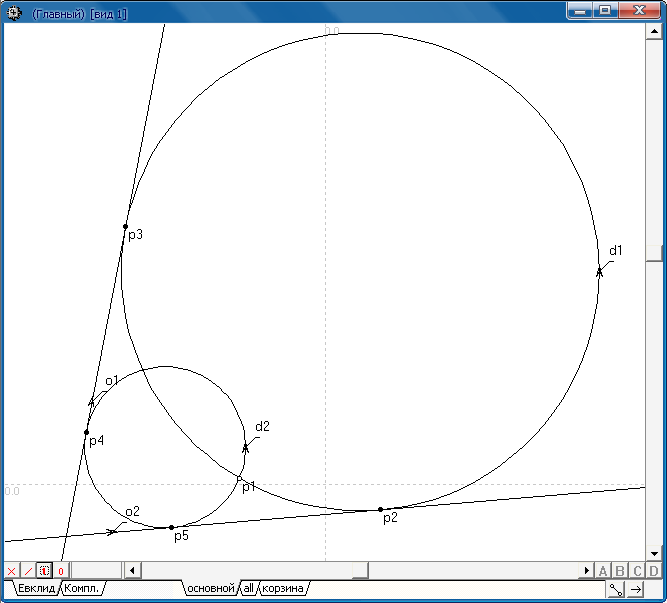
Пример 1:
Построить две окружности, сопрягающие две заданные прямые o1 и o2 и проходящие через заданную точку p1.
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -255.5 , Y1= -33.5 , X2= -210.5 , Y2= 199.5 . |
2 |
|
Прямая o2 задана координатами двух точек: X1= -409.5 , Y1= -64.5 , X2= -16.5 , Y2= -31.5 . |
3 |
|
Точка p1 задана координатами -85.5 и 6.5 . |
4 |
|
Окружности d1 и d2 касаются в точках p2 , p3 и p4 , p5 объектов o2 и o1 и проходят через точку p1 . |
|

Пример 2:
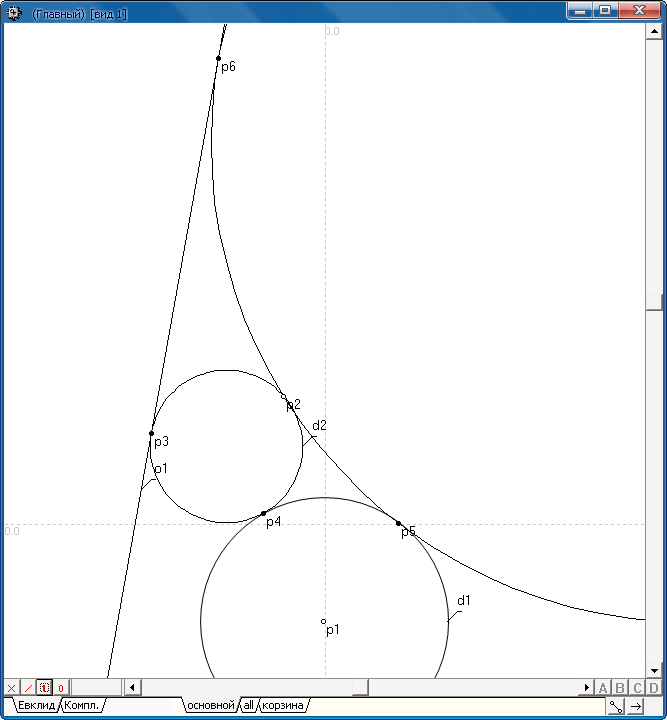
Построить две окружности, сопрягающие прямую o1 и окружность d1 и проходящие через заданную точку p1.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -1.5 и -96.5 . |
2 |
|
Окружность d1 задана центром p1 и радиусом 123.5 . |
3 |
|
Прямая o1 задана координатами двух точек: X1= -212.5 , Y1= -126.5 , X2= -154.5 , Y2= 197.5 . |
4 |
|
Точка p2 задана координатами -41.5 и 128.5 . |
5 |
|
Окружности d2 и d3 касаются в точках p3 , p4 и p5 , p6 объектов o1 и d1 и проходят через точку p2 . |
|

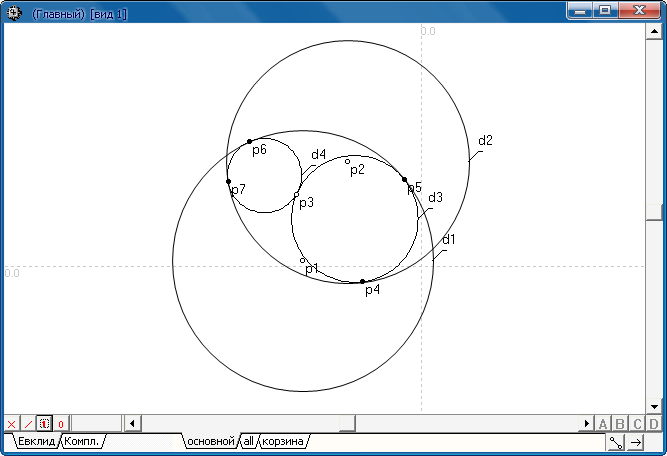
Пример 3:
Построить две окружности, сопрягающие две заданные окуржности d1 и d2 и проходящие через заданную точку p1.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -118.5 и 6.5 . |
2 |
|
Окружность d1 задана центром p1 и радиусом 130.1 . |
3 |
|
Точка p2 задана координатами -73.5 и 105.5 . |
4 |
|
Окружность d2 задана центром p2 и радиусом 121.2 . |
5 |
|
Точка p3 задана координатами -124.5 и 72.5 . |
6 |
|
Окружности d3 и d4 касаются в точках p4 , p5 и p6 , p7 объектов d2 и d1 и проходят через точку p3 . |
|

|
| |
|
| |
|
| |
|
| |
| |
|