Способы преобразования чертежа применяются для приведения геометрических объектов в частное положение относительно плоскостей проекций, что позволяет упростить решение ряда позиционных и метрических задач.

Способы преобразования чертежа можно разделить на две группы:

1. Способы дополнительного проецирования. Эти способы основаны на введение дополнительных плоскостей проекций и центров проецирования. При этом положение геометрических объектов по отношению к исходным плоскостям проекций π1 и π2 остается неизменным.
2. Способы перемещения или вращения геометрических объектов. Эти способы основаны на изменении положения геометрических объектов по отношению к исходным плоскостям проекций π1 и π2. В этой части курса будем рассматривать только один из первой группы способов преобразования чертежа – способ дополнительного ортогонального проецирования.

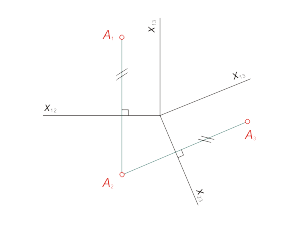
Возьмем в пространстве дополнительную плоскость π3 перпендикулярную плоскости π2 (π3 ⊥ π2) и составляющую с плоскостью π1 произвольный угол φ. Проецирование на плоскость π3 из несобственного центра S3∞ выберем ортогональным (аналогично проецированию на плоскости π1 и π2 из соответствующих центров S1∞ и S2∞) (рис. 3.1).

Для построения проекции A3 произвольной точки А исходного пространства выполним следующие операции:

1. Через центр S3∞ и точку А проведем прямую a;
2. Отметим точку пересечения прямой a с плоскостью π3: A3=a ∩ π3.

Полученная точка A3 будет называться дополнительной ортогональной проекцией точки А на плоскость π3 из центра S3∞.

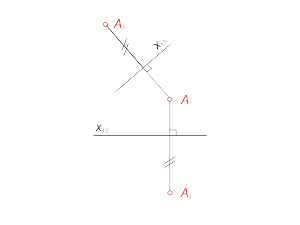
Из рисунка 3.1 видно, что расстояние от точки A до плоскости π2 равно расстоянию от точки А1 до оси x12, а также расстоянию от точки А3 до оси x23: | A , π2| = | A1, x12| = | A3, x13|.

Для перехода к плоской модели повернем плоскость π3 вокруг оси x23 до совмещения с плоскостью π2, а затем - плоскость π2 вокруг оси x12 до совмещения с плоскостью π1.

Положение проекции А3 точки А на плоской модели определим следующим образом:
- из точки А2 проведем линию связи перпендикулярно оси x23 (рис.3.2);
- измерим расстояние от проекции А1 до оси x12 и отложим это значение по линии связи от оси x23 .

Если взять дополнительную плоскость π3 перпендикулярно плоскости π1, то в этом случае положение проекции А3 на плоской модели определится следующим образом:
- из точки А1 проведем линию связи перпендикулярно прямой x13 (рис.3.3);
- измерим расстояние от проекции А2 до оси x12 и отложим это значение по линии связи от оси x13 .

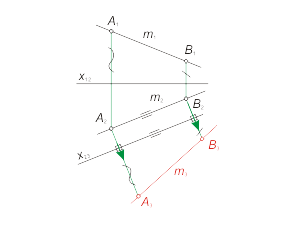
Рассмотрим ряд задач, связанных с приведением геометрических объектов в частное положение относительно плоскостей проекций и определением некоторых метрических характеристик этих объектов способом ДОП.

Задача 3.1. Преобразовать прямую общего положения (m) в прямую уровня.

Для решения этой задачи дополнительная плоскость проекций π3 выбирается параллельно прямой m и перпендикулярно одной из плоскостей проекций. Если π3 ⊥ π2, то на плоской модели ось x23 будет параллельна m2 (x23 || m2) (рис. 3.4).

Алгоритм решения

1. Проведем ось x23 параллельно проекции m2 на произвольном расстоянии от нее.
2. Отметим на прямой m две точки - точки A(A1- A2) и B(B1- B2).
3. Определим проекции A3, B3 точек A и B в дополнительном поле проекций π3 в соответствии с рис. 3.2.

В новой системе плоскостей (π2-π3) прямая m(m2-m3) преобразовалась в линию уровня.

Используя это преобразование можно измерить длину отрезка AB, а также углы между отрезком и плоскостями проекций (рис. 3.5).

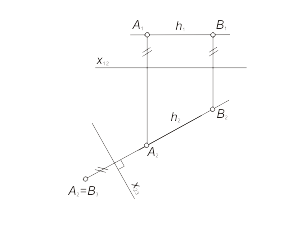
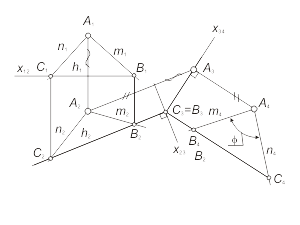
Задача 3.2. Преобразовать прямую уровня (h) в проецирующую прямую (рис. 3.6).

Для решения этой задачи дополнительная плоскость π3 выбирается перпендикулярно прямой.

Так как по условию задачи прямая h параллельна плоскости π2, очевидно, что плоскость π3 будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось x23 - перпендикулярна h2.

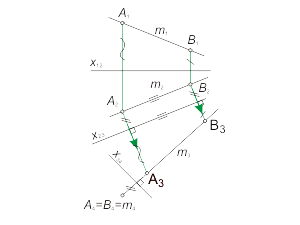
Алгоритм решения

1. Проведем ось x23 перпендикулярно проекции h2 .
2. Отметим на прямой h две точки - точки A(A1- A2) и B(B1- B2).
3. Определим проекции A3, B3 точек A и B в дополнительном поле проекций π3 в соответствии с рис. 3.2 .

В новой системе плоскостей (π2-π3 ) прямая h(h2-h3) преобразовалась в проецирующую прямую. Преобразование прямой общего положения в проецирующую прямую осуществляется в два этапа. На первом этапе прямая общего положения преобразуется в прямую уровня (задача 3.1). Затем, при введении еще одной дополнительной плоскости - π4, прямая уровня преобразуется в проецирующую прямую (задача 3.2). На рис. 3.7 приведен пример преобразования прямой общего положения (m) в проецирующую.

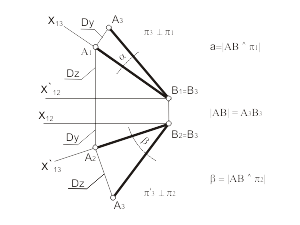
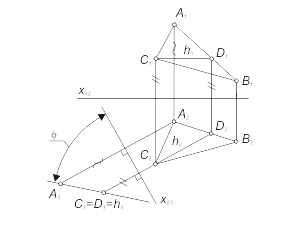
Для построения проекций точек в поле π4 расстояния измеряем в поле проекций π2 (от точек A2, B2 до оси x23) и откладываем в поле π4 от оси x34 по линии проекционной связи, перпендикулярной x34.

Задача 3.3. Преобразовать плоскость α(А, В, С) общего положения в проецирующую.

Исходя из определения проецирующей плоскости, дополнительная плоскость проекций π3 должна быть перпендикулярна прямой, принадлежащей этой плоскости. Учитывая, что дополнительная плоскость перпендикулярна π1 или π2, - π3 выберем перпендикулярной одной из фронтали или горизонтали плоскости α соответственно.

Возьмем π3 перпендикулярно горизонтали h плоскости α. Очевидно, что при этом плоскость π3 будет перпендикулярна горизонтальной плоскости проекций, а на плоской модели ось x23 - перпендикулярна h2 (рис. 3.8).

Алгоритм решения

1. Построим горизонталь h (h1- h2) плоскости α(А, В, С).
2. Проведем ось x23 перпендикулярно проекции h2 .
3. Определим проекции горизонтали h и точки A в дополнительном поле проекций π3 – совпавшие проекции С3, D3 и проекция A3.
4. Через точки A3 и С3(D3) проведем прямую (α3) - вырожденную проекцию плоскости α.

В новой системе плоскостей (π2-π3) плоскость a преобразовалась в проецирующую плоскость.

Используя это преобразование можно измерить угол (φ) между плоскостью общего положения (α) и плоскостью проекций π2. Для определения угла между плоскостью общего положения и плоскостью π1 дополнительную плоскость π3 нужно задать перпендикулярно фронтали плоскости α и выполнить аналогичные преобразования.

Задача 3.4. Преобразовать проецирующую плоскость α(А, В, С) в плоскость уровня.

Исходя из определения плоскости уровня, дополнительная плоскость проекций π3 должна быть параллельна плоскости α. Так как плоскость α по условию задачи является фронтально-проецирующей (рис. 3.9), очевидно, что плоскость π3 будет перпендикулярна фронтальной плоскости проекций, а на плоской модели ось x13 - параллельна α1 .

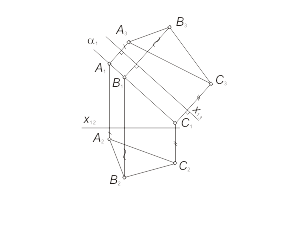
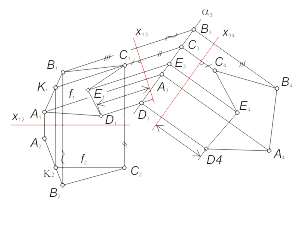
Алгоритм решения

1. Проведем ось x13 параллельно проекции α1 на произвольном расстоянии от нее.
2. Определим проекции A3, B3 и С3 точек A, B и С в дополнительном поле проекций π3 в соответствии с рис. 3.3.

В новой системе плоскостей (π1-π3) плоскость a преобразовалась в плоскость уровня. По проекции треугольника в поле π3 можно определить все его метрические характеристики.

Это преобразование используется в практике черчения для построения натуральной величины наклонного сечения детали.

Преобразование плоскости общего положения в плоскость уровня осуществляется в два этапа. На первом этапе плоскость общего положения преобразуется в проецирующую (задача 3.3). Затем, при введении еще одной дополнительной плоскости - π4, проецирующая плоскость преобразуется в плоскость уровня (задача 3.4).

На рис. 3.10 приведен пример преобразования плоскости общего положения в плоскость уровня. Используя это преобразование можно определить угол между пересекающимися прямыми m и n.

Если плоскость общего положения будет задана некоторой фигурой α(А, В, С, E, D) (рис. 3.11), то подобное преобразование позволит определить размеры и форму плоской фигуры.