|
||||
 |
||||
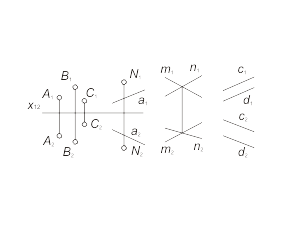
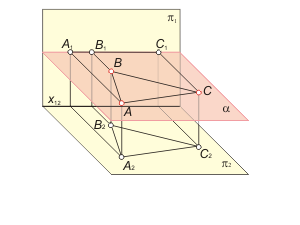
The methods of plane definition (fig. 1.20):
1. The three noncolinear points - α(A, B, C). 2. The line and the noncoincident point - α(N, a). 3. Two crossing or two parallel lines - α(m, n), α(c, d). |
Fig. 1-20 |
|||
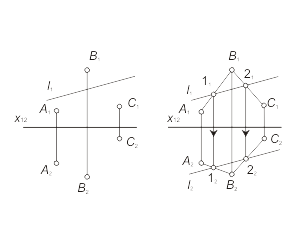
Task # 1.2 Define the model of any straight line, coincident with the plane α(А, В, С). |
Fig. 1-21 |
|||
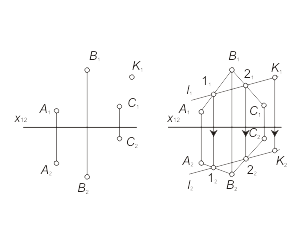
Algorithm: |
Fig. 1-22
|
|||
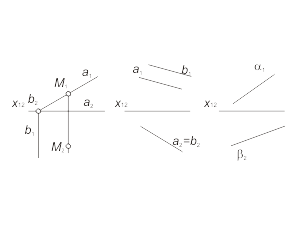
The planes of special positioning Projective planes The plane, that is coincident with the projective line, is called as projective plane. It's obvisual, that the frontal-projective plane is perpendicular with the plane π1 (fig. 1.23), and horizontal-projective plane is perpendicular with the plane π2. The fig. 1.23 shows, that frontal projections of all elements of the plane α(a,b) are situated on a single line a1. This line is called as plane's degenerative projection and possess a collective property. The fig. 1.24 represents frontal-projective image of a plane α and horizontal-projective image of a plane β. |
Fig. 1-23 Fig. 1-24 |
|||
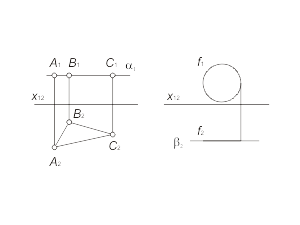
The fig. 1.25 represents the plane α, that is parallel with the horizontal plane of projections. The triangle ABC, that belongs to the plane α, would be projected at a plane π2 without any distortions. So it is possible to estimate the initial spape an size of triangle by the means of its image. The fig. 1.26 represent the projections of level-plane α, that is parallel with π2, and plane β, that is parallel with π1. |
Fig. 1-25 Fig. 1-26 |
|||
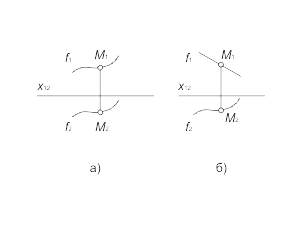
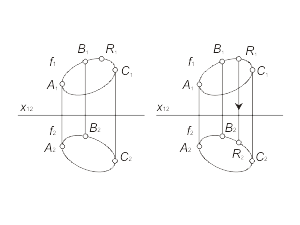
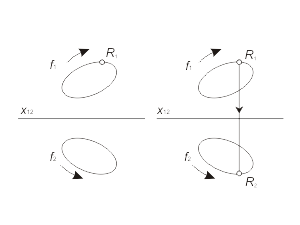
 It is possible to determine the curved line, like a trajectory of a moving point, or like a set of points, unified with some common property. The curved line also can be defined like the mutual cross-section of two surfaces. All curved lines are classified as planar or volumetric. Если все точки кривой расположены в одной плоскости, то такая линия называется плоской. Кривая линия, которая не может быть совмещена с плоскостью всеми своими точками, называется пространственной, например винтовая линия. Моделью кривой линии в общем случае является пара кривых линий f ( f1, f2 ) (fig. 1.27 а). It is possible to determine the curved line, like a trajectory of a moving point, or like a set of points, unified with some common property. The curved line also can be defined like the mutual cross-section of two surfaces. All curved lines are classified as planar or volumetric. Если все точки кривой расположены в одной плоскости, то такая линия называется плоской. Кривая линия, которая не может быть совмещена с плоскостью всеми своими точками, называется пространственной, например винтовая линия. Моделью кривой линии в общем случае является пара кривых линий f ( f1, f2 ) (fig. 1.27 а). В частном случае, когда плоская кривая принадлежит проецирующей плоскости, она моделируется прямой и кривой линией (fig. 1.27 б). Построение произвольной точки M, принадлежащей кривой линии f , выполняется по тем же правилам, как и для прямой линий. |
Fig. 1-27 |
|||
|
Fig. 1-28 Fig. 1-29 |
||||
 Порядок кривой линии Порядок кривой линии Наибольшее число точек пересечения плоской кривой с прямой линией определяет порядок плоской кривой. Наибольшее число точек пересечения пространственной кривой линии с плоскостью определяет порядок пространственной кривой. Рассмотрим некоторые кривые линии, наиболее широко применяемые на практике. Среди плоских кривых линий особого внимания заслуживают кривые второго порядка в виду их широкого применения в ряде разделов физики, в астрономии, механике, архитектуре и других областях науки и техники. Известно, например, что планеты движутся по эллипсам. Траекториями движения твердого тела могут быть эллипс и парабола. Направленные под углом к горизонту снаряды, неуправляемые баллистические ракеты движутся по параболам. |
||||
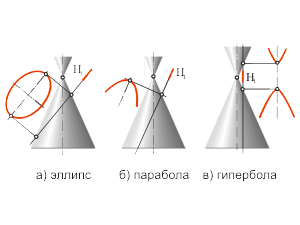
 Conics ConicsКривые второго порядка называются коническими сечениями, так как они могут быть получены при пересечении поверхности прямого кругового конуса плоскостью. В зависимости от положения секущей плоскости σ по отношению к образующим конуса получаются различные кривые второго порядка: - эллипс или окружность, когда плоскость пересекает все образующие (эти линии не имеют несобственных точек) (fig. 1.30 а); - парабола, когда секущая плоскость параллельна одной образующей (парабола имеет одну несобственную точку) (fig. 1.30 б); - гипербола, когда плоскость параллельна двум образующим (гипербола имеет две несобственные точки) (fig. 1.30 в); - кривая, распавшаяся на пару прямых, когда плоскость проходит через вершину конуса. При параллельном проецировании проекцией эллипса и окружности является эллипс или, в частном случае, окружность, проекцией параболы является парабола, проекцией гиперболы – гипербола. |
||||
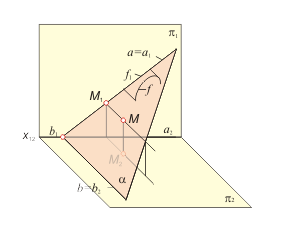
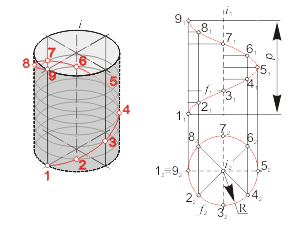
Algorithm: |
Fig. 1-31
|
|||