Краткое содержание лекции 1 |
|
|
|
|
|
|
Начертательная геометрия изучает методы отображения объектов трехмерного пространства на плоскость и способы графических решений позиционных и метрических задач, связанных с этими объектами, по их плоским отображениям (моделям). |
|
| |
Часть первая. Моделирование геометрических образов |
| |
Простейшим образом (элементом) пространства является точка. Точки могут быть собственными и несобственными (бесконечно удаленными). На модели стрелкой будем обозначать направление на несобственную точку. Все остальные геометрические объекты (линия, плоскость, поверхность…) можно представить, как множество точек. Для моделирования объектов трехмерного пространства будем использовать операцию проецирования. |
|
| |
|
| |
Выберем в пространстве точку S1 – центр проецирования и плоскость π1 – плоскость проекций (рис. 1.1). Центр S1 и плоскость проекций π1 представляют собой аппарат проецирования. Для построения проекции произвольной точки А исходного пространства выполним следующие операции:
1. Через центр S1 и точку А проведем прямую a;
2. Отметим точку пересечения прямой a с плоскостью π1: A1=a ∩ π1.
Полученная точка A1 называется проекцией точки A (образом A) на плоскость π1 из центра S1. Аналогично строятся проекции других точек пространства. Прямая линия – a, проходящая через центр S1 называется проецирующей прямой и на плоскости проекций отображается (проецируется) точкой. В зависимости от положения центра S1, проецирование может быть центральным или параллельным.
В случае, когда S1 является собственной точкой пространства, получаем аппарат центрального проецирования (рис. 1.1). При центральном проецировании проекцией несобственной точки D∞ может быть собственная точка D1.
Удалив центр проецирования S1 в бесконечность, получим аппарат параллельного проецирования (рис. 1.2). При параллельном проецировании проекцией несобственной точки D∞ всегда будет несобственная точка D1∞. Если направление параллельного проецирования составляет с плоскостью π1 угол φ≠90°, то получаем аппарат косоугольного проецирования.
В частном случае параллельного проецирования, когда угол φ=90°, т.е. проецирующие лучи перпендикулярны плоскости проекций, получаем аппарат прямоугольного (ортогонального) проецирования. |
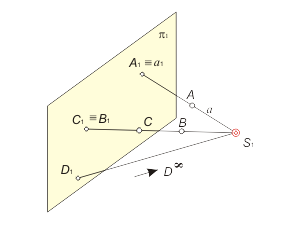
Рис. 1.1
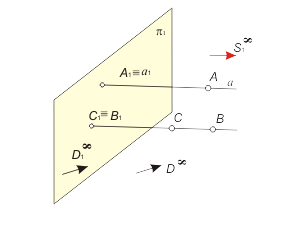
Рис. 1.2 |
| |
Свойства параллельного проецирования |
| |
1. Проекция точки есть точка.
2. Проекцией прямой является прямая линия. Проекция проецирующей прямой вырождается в точку.
3. Инцидентность (взаимопринадлежность) точек и линий сохраняется. Из этого свойства вытекает следствие: проекции пересекающихся между собой линий пересекаются в точке, которая является проекцией точки пересечения этих линий.
4. Проекции параллельных прямых параллельны между собой.
5. Отношение длин проекций двух параллельных отрезков равно отношению длин проецируемых отрезков.
6. Параллельная проекция фигуры, расположенной в плоскости, параллельной плоскости проекций, конгруэнтна (равна) самой фигуре.
Рассмотренные модели, полученные методом центрального или параллельного проецирования, являются необратимыми. Множеству точек, расположенных на проецирующей прямой a, соответствует на плоскости проекций одна точка A1. Из этого следует, что одной и той же проекции объекта на картине π1 будет соответствовать в пространстве множество объектов. Для получения обратимой модели, по которой можно восстановить форму, размеры и положение объекта в пространстве, используют метод двух изображений. |
|
| |
|
| |
Французский математик Гаспар Монж (1746 - 1818 г.г.) предложил получать отображения предметов пространства, используя прямоугольное проецирование на две взаимно перпендикулярные плоскости. Возьмем в пространстве две взаимно перпендикулярные плоскости – π1 ⊥ π2. Плоскость π1 называется фронтальной плоскостью проекций, а π2 – горизонтальной плоскостью проекций. Проецирование на плоскости π1 и π2 из соответствующих центров S1∞ и S2∞ - ортогональное (рис. 1.3) Для перехода к плоской модели будем поворачивать плоскость π2 вокруг оси x12 до совмещения с плоскостью π1. |
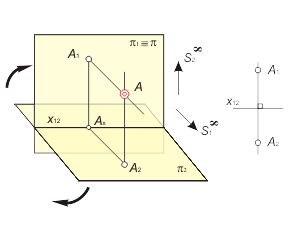
Рис. 1.3
|
| |
|
| |
Модель точки А на эпюре Монжа представляет собой пару точек А1 и А2, расположенных на одной линии связи, перпендикулярной оси x12.
Рассмотрим возможные положения проекций точек на эпюре Монжа относительно оси x12 в зависимости от их положения в исходном пространстве относительно плоскостей проекций π1 и π2. На рис. 1.4 показано расположение точек А, В, С, D соответственно в I, II, III и IV четвертях пространства, а на эпюре Монжа (рис. 1.5) даны возможные варианты расположения их проекций относительно оси x12. |
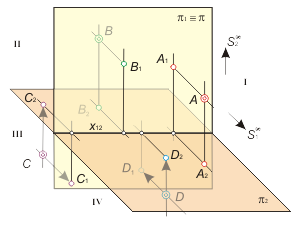
Рис. 1.4
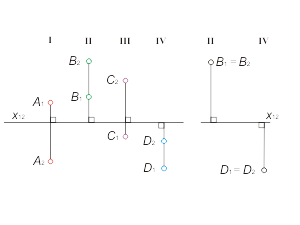
Рис. 1.5 |
| |
|
| |
Две точки, лежащие на одной проецирующей прямой, называются конкурирующими. На эпюре Монжа с помощью проекций конкурирующих точек можно определять взаимную видимость геометрических фигур.
На рис 1.6 представлены две пары конкурирующих точек A, B (АВ ⊥ π1) и C, D (CD ⊥ π2 ). Стрелками показано направление взгляда наблюдателя на плоскости проекций. Видимой считают ту точку, которая находится ближе к наблюдателю (центру проецирования). При проецировании на плоскость π1 видимой будет точка A, а при проецировании на плоскость π2 – точка С. |
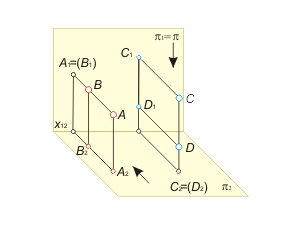
Рис. 1.6 |
| |
Моделирование декартовой пространственной системы координат |
| |
Для определения местоположения точки в пространстве будем использовать прямоугольную декартову систему координат (xyz), которая представляет собой три взаимно перпендикулярные оси (рис. 1.7). |
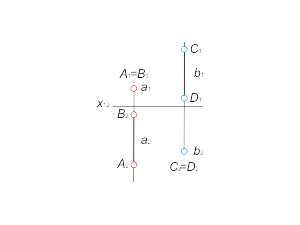
Рис. 1.7 |
В этой системе точка A задается координатами (xA, yA, zA). Координаты точки могут быть, как положительными, так и отрицательными.
Для моделирования системы координат на эпюре Монжа выполним следующие операции:
– совместим координатную плоскость xOz с фронтальной плоскостью проекций π1, а координатную плоскость xOy с горизонтальной плоскостью проекций π2 (рис. 1.8);
– осуществим переход к одной плоскости – эпюру Монжа.
На рис. 1.9 отображены проекции осей координат x, y, z, а также проекции точки А. |
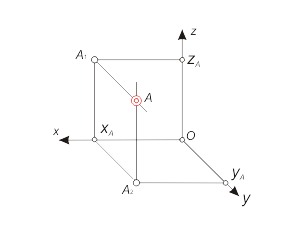
Рис. 1.8
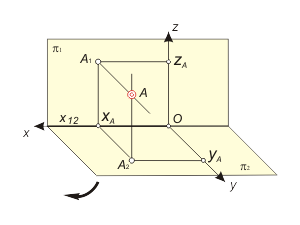
Рис. 1.9 |
Очевидно, что фронтальная проекция А1 точки А, будет определяться координатами (xA, zA), а горизонтальная проекция А2 – координатами (xA, yA).
Положительные значения (xA, yA, zA) будут отмечаться от точки O(О1, О2) влево, вниз и вверх на проекциях x1, y2 и z1 соответственно, отрицательные же значения (xA, yA, zA) - от точки O(О1,О2) вправо, вверх и вниз на проекциях x2, y2 и z1 соответственно. На рис. 1.10 представлены проекции точек А, В, С, D с координатами: А(30, 40, 30); В(60, -40, 20); С(40, -20, -20); D(10, 10, -30). |
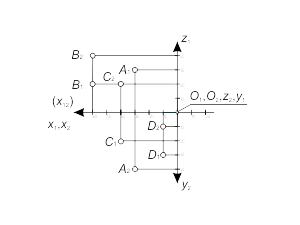
Рис. 1.10 |
Как уже известно, две проекции точки вполне определяют ее положение в пространстве. Однако, при решении задач начертательной геометрии, а также при построении технических чертежей объектов часто используют профильную плоскость π3(π1 ⊥ π3 ⊥ π2).
При моделировании прямоугольной системы координат будем совмещать плоскость π3 с координатной плоскостью (yOz) (рис. 1.11), тогда профильная проекция А3 точки А определится координатами (yA, zA). При переходе к плоской модели будем поворачивать плоскость π3 вокруг оси x13 до совмещения с плоскостью π1. |
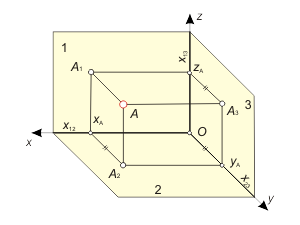
Рис. 1.11 |
Так как координата zA будет общей для проекций А3 и А1, а координата yA – для проекций А3 и А2, то положение проекции А3 на плоской модели можно определить следующим образом:
– провести прямую (линию связи) из точки А1 перпендикулярно прямой z1(x13) (рис.1.12);
– на линии связи от прямой z1(x13) отложить расстояние равное по значению координате yA, или, другими словами, измерить расстояние от проекции А2 до оси x12 и отложить это значение по линии связи от оси x13.
|
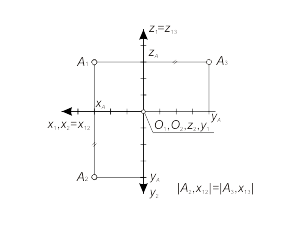
Рис. 1.12 |
| |
| |
|
|
|












