Объект в квадратичной инволюции |
|
| |
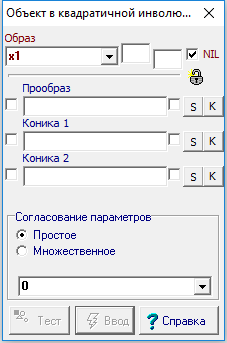
Отношение предназначено для построения Образа объекта (точки или прямой линии)-Прообраза в преобразовании квадратичной инволюции, определенном двумя кривыми второго порядка Коника 1 и Коника 2.
Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.
|
|
| |
| |
| |
Клавиша |
Предварительно
выделено: |
Действие |
Выделение
после
действия: |
 |
I |
Произвольные объекты,
последние два - коники |
Построение образов выделенных объектов функцией  в преобразовании квадратичной инволюции, определенной последними двумя выделенными кониками в преобразовании квадратичной инволюции, определенной последними двумя выделенными кониками |
Выделяются объекты преобразования |
|
| |
| |
|
Параметры |
Типы объектов |
Функциональное назначение параметров |
|
Образ |
Точка, коника |
Результат преобразования (точка или коника)
|
|
Прообраз |
Точка, прямая |
Исходные точка или прямая
|
|
Коника 1 |
Коника |
Первая коника, задающая преобразование |
|
Коника 2 |
Коника |
Вторая коника, задающая преобразование
|
|
| |
Прототип команды: YK Согласование Образ ; Прообраз Коника1 Коника2 .
|
| |
Пояснение к реализации функции:
Входной параметр: p11.
Выходной параметр: p12.
Результат преобразования находится, как точка пересечения поляр, построенных для исходной точки как для полюса по отношению к двум исходным коникам.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -258.5 и -11.5 . |
2 |
|
Точка p2 задана координатами -266.5 и 80.5 . |
3 |
|
Точка p3 задана координатами -172.5 и 131.5 . |
4 |
|
Точка p4 задана координатами -79.5 и 102.5 . |
5 |
|
Точка p5 задана координатами -110.5 и -21.5 . |
6 |
|
Коника y1 по точкам p1 , p2 , p3 , p4 , p5 . |
7 |
|
Точка p6 задана координатами 23.5 и 13.5 . |
8 |
|
Точка p7 задана координатами 55.5 и 131.5 . |
9 |
|
Точка p8 задана координатами 118.5 и 162.5 . |
10 |
|
Точка p9 задана координатами 142.5 и 121.5 . |
11 |
|
Точка p10 задана координатами 138.5 и -4.5 . |
12 |
|
Коника y2 по точкам p6 , p7 , p8 , p9 , p10 . |
13 |
|
Точка p11 задана координатами -7.5 и -73.5 . |
14 |
|
Поляра o1 точки p11 относительно коники y1 . |
15 |
|
Поляра o2 точки p11 относительно коники y2 . |
16 |
|
Точка p12 есть пересечение прямых o1 и o2 . |
|


структура функции |
| |
| |
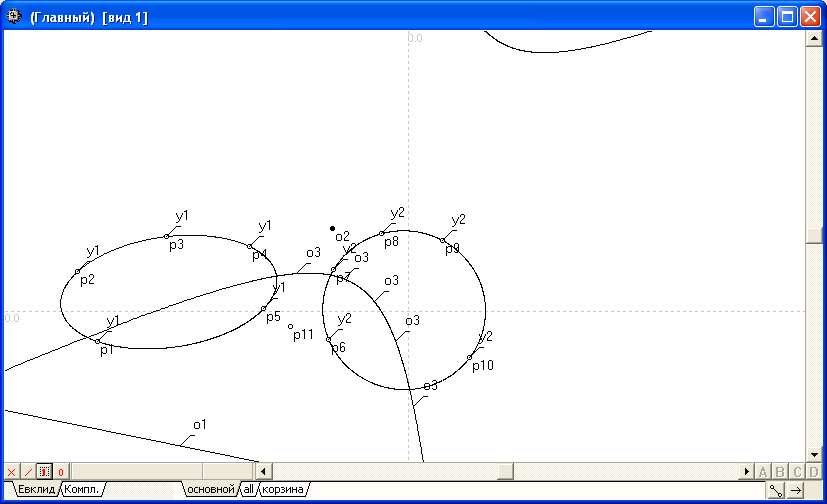
Пример:
Построить образы точки p11 и прямой o1 в квадратичной инволюции, заданной кониками y1 и y2.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -310.5 и -30.5 . |
2 |
|
Точка p2 задана координатами -330.5 и 39.5 . |
3 |
|
Точка p3 задана координатами -241.5 и 74.5 . |
4 |
|
Точка p4 задана координатами -158.5 и 64.5 . |
5 |
|
Точка p5 задана координатами -144.5 и 2.5 . |
6 |
|
Коника y1 по точкам p1 , p2 , p3 , p4 , p5 . |
7 |
|
Точка p6 задана координатами -79.5 и -28.5 . |
8 |
|
Точка p7 задана координатами -74.5 и 41.5 . |
9 |
|
Точка p8 задана координатами -26.5 и 77.5 . |
10 |
|
Точка p9 задана координатами 34.5 и 70.5 . |
11 |
|
Точка p10 задана координатами 61.5 и -46.5 . |
12 |
|
Коника y2 по точкам p6 , p7 , p8 , p9 , p10 . |
13 |
|
Точка p11 задана координатами -118 и -15.5 . |
14 |
|
Прямая o1 задана координатами двух точек: X1= -407.5 , Y1= -98.5 , X2= -48.5 , Y2= -170.5 . |
15 |
|
Образ o2 прообраза p11 в квадратичной инволюции на кониках y1 и y2 . |
16 |
|
Образ o3 прообраза o1 в квадратичной инволюции на кониках y1 и y2 . |
|

|
| |
|
| |
|
| |
|
| |
|