Симедианы треугольника

Отношение предназначено для построения симедиан треугольника. Симедианой называется прямая линия, которая симметрична лучу медианы относительно биссектрисы угла, проведенной из той же вершины треугольника. См. также симедианы.

Если тип объекта, указанного во входном параметре, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.

Параметры	Типы объектов	Функциональное назначение параметров
Симедиана 1	Прямая	Симедиана, исходящая из точки пересечения первой и третьей сторон треугольника
Симедиана 2	Прямая	Симедиана, исходящая из точки пересечения первой и второй сторон треугольника
Симедиана 3	Прямая	Симедиана, исходящая из точки пересечения второй и третьей сторон треугольника
Первая сторона треугольника	Прямая	Первая сторона треугольника
Вторая сторона треугольника	Прямая	Вторая сторона треугольника
Третья сторона треугольника	Прямая	Третья сторона треугольника

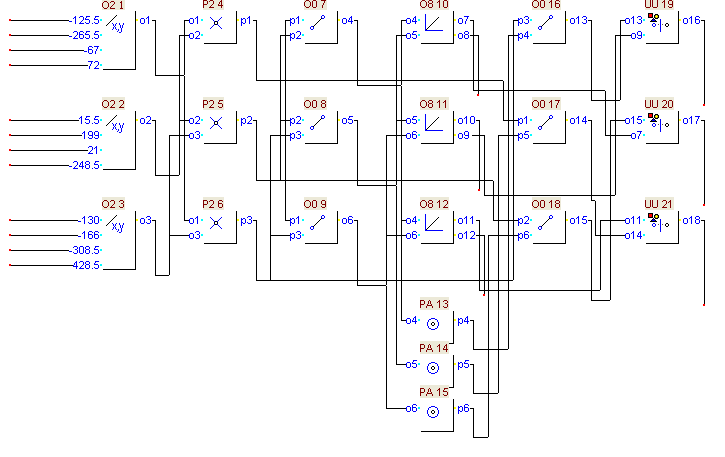
Прототип команды: TR013 Согласование Симедиана_1 Симедиана_2 Симедиана_3 ; Первая_сторона_треугольника Вторая_сторона_треугольника Третья_сторона_треугольника .

Входные параметры: o1, o2, o3.

Выходные параметры: o9, o7, o11.

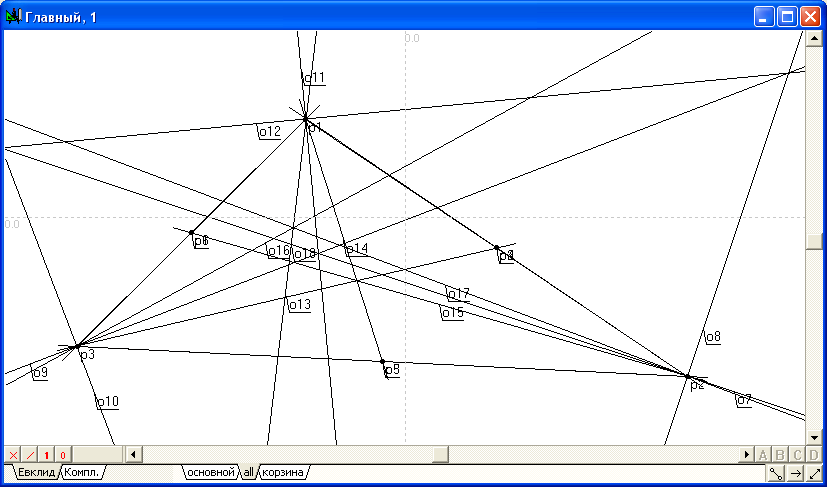
Алгоритм "Главный"

1		Прямая o1 задана координатами двух точек: X1= -265.5 , Y1= -67 , X2= -125.5 , Y2= 72 .
2		Прямая o2 задана координатами двух точек: X1= -248.5 , Y1= 199 , X2= 15.5 , Y2= 21 .
3		Прямая o3 задана координатами двух точек: X1= 428.5 , Y1= -166 , X2= -308.5 , Y2= -130 .
4		Точка p1 есть пересечение прямых o1 и o2 .
5		Точка p2 есть пересечение прямых o2 и o3 .
6		Точка p3 есть пересечение прямых o3 и o1 .
7		Прямая o4 задана точками p1 и p2 .
8		Прямая o5 задана точками p2 и p3 .
9		Прямая o6 задана точками p3 и p1 .
10		Бисcектрисы o7 и o8 в угле, образованном прямыми o4 и -o5 .
11		Бисcектрисы o9 и o10 в угле, образованном прямыми o5 и -o6 .
12		Бисcектрисы o11 и o12 в угле, образованном прямыми o6 и -o4 .
13		Точка p4 есть центр объекта o4 .
14		Точка p5 есть центр объекта o5 .
15		Точка p6 есть центр объекта o6 .
16		Прямая o13 задана точками p3 и p4 .
17		Прямая o14 задана точками p1 и p5 .
18		Прямая o15 задана точками p2 и p6 .
19		Объект o16 симметричен относительно оси o9 объекту o13 .
20		Объект o17 симметричен относительно оси o7 объекту o15 .
21		Объект o18 симметричен относительно оси o11 объекту o14 .

Структура функции

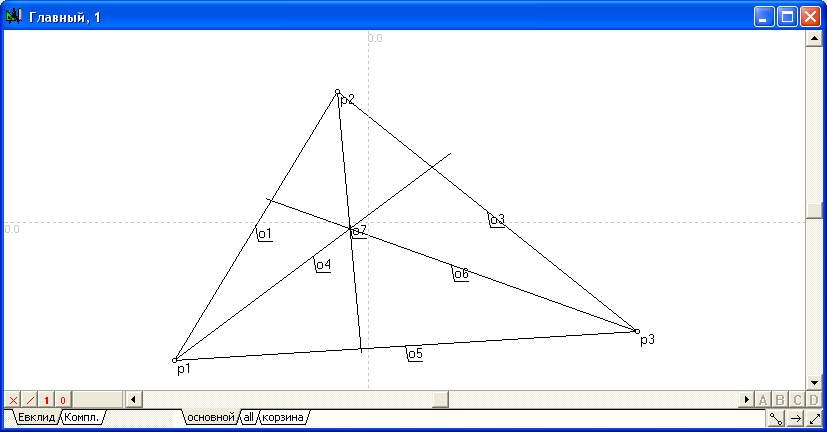
Пример 1:

Построить симедианы треугольника, заданного вершинами p1, p2 и p3.

Алгоритм "Главный"

1		Точка p1 задана координатами -115 и -82 .
2		Точка p2 задана координатами -18 и 78 .
3		Точка p3 задана координатами 160 и -65 .
4		Прямая o1 задана точками p1 и p2 .
5		Прямая o3 задана точками p2 и p3 .
6		Прямая o5 задана точками p3 и p1 .
7		Прямые o4 , o6 , o7 - симедианы треугольника, построенного на прямых o1 , o3 , o5 .