|
|||
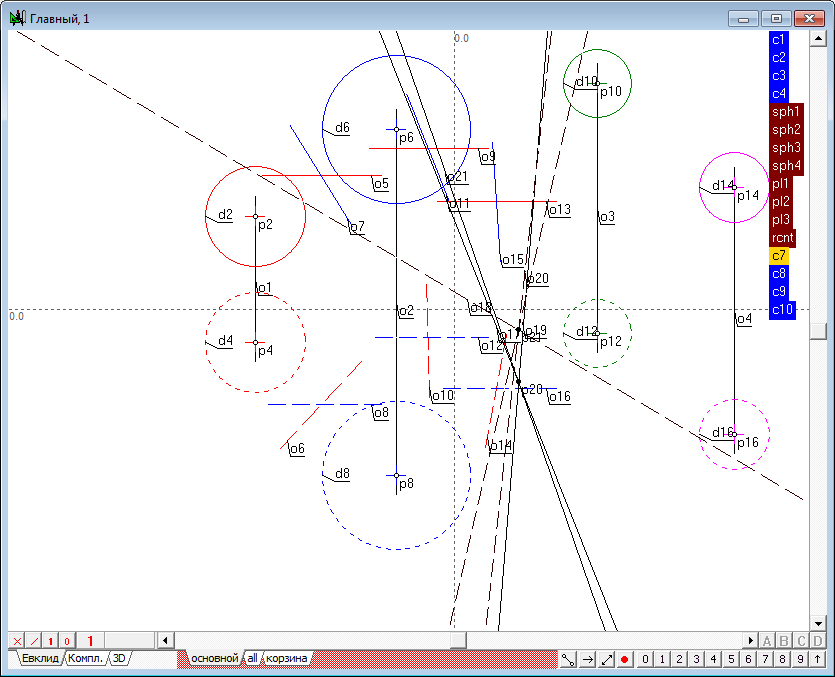
Построим сферу, проходящую ортогонально к четырем заданным сферам. Задача сводится к решению следующих подзадач: - построение радикальных плоскостей для трех пар исходных сфер; |
|||
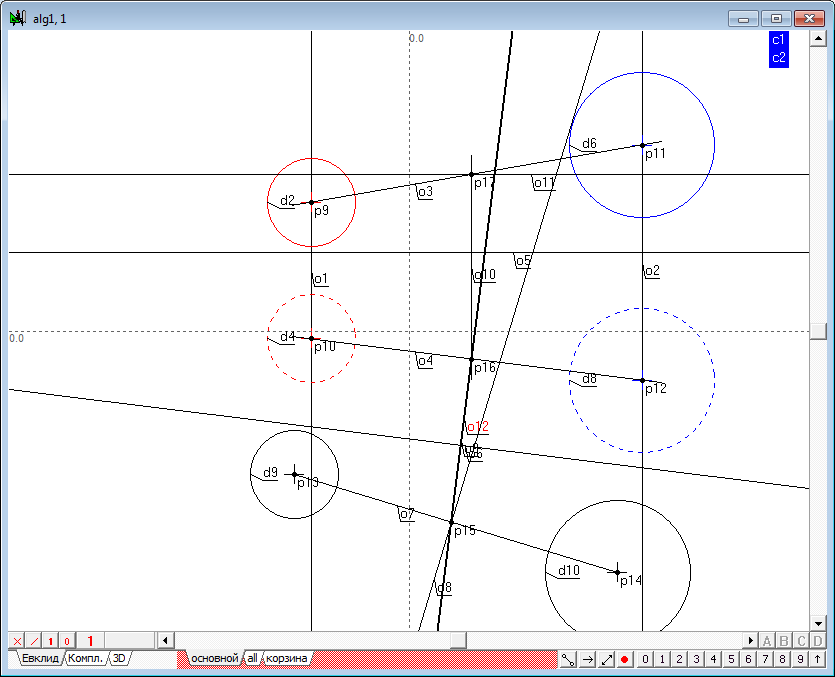
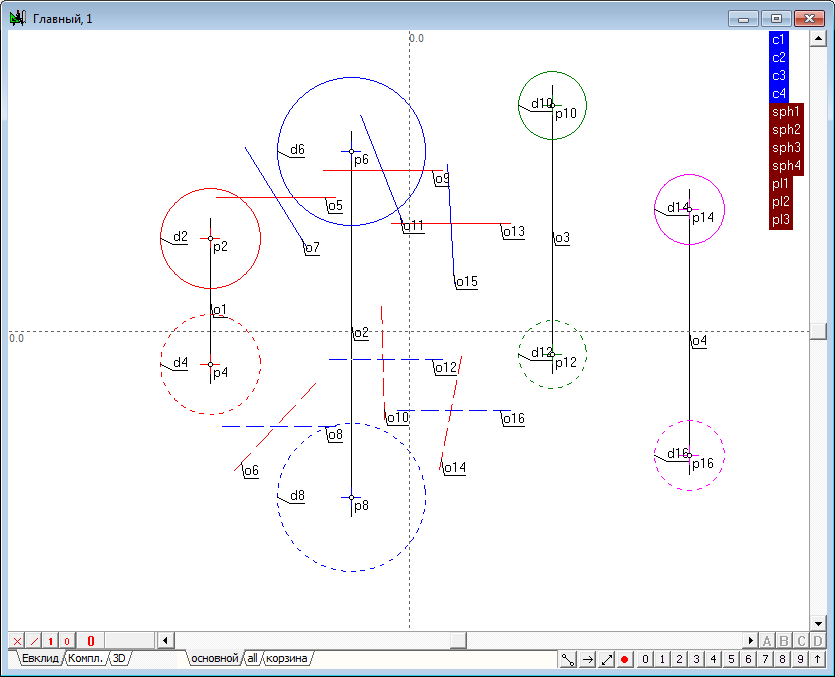
| 1 | Приступим к реализации алгоритма решения задачи. Откроем новый проект и зададим в окне главного алгоритма модели четырех сфер. Для этого воспользуемся инструментом Свободная окружность. Перед началом формирования сфер убедимся в том, что индикатор количества проекций установлен в значение 2. Если это не так, то, расположив курсор над этим индикатором, правой кнопкой мыши следует вызвать контекстное меню, в котором необходимо выбрать и установить требуемое значение. |
||
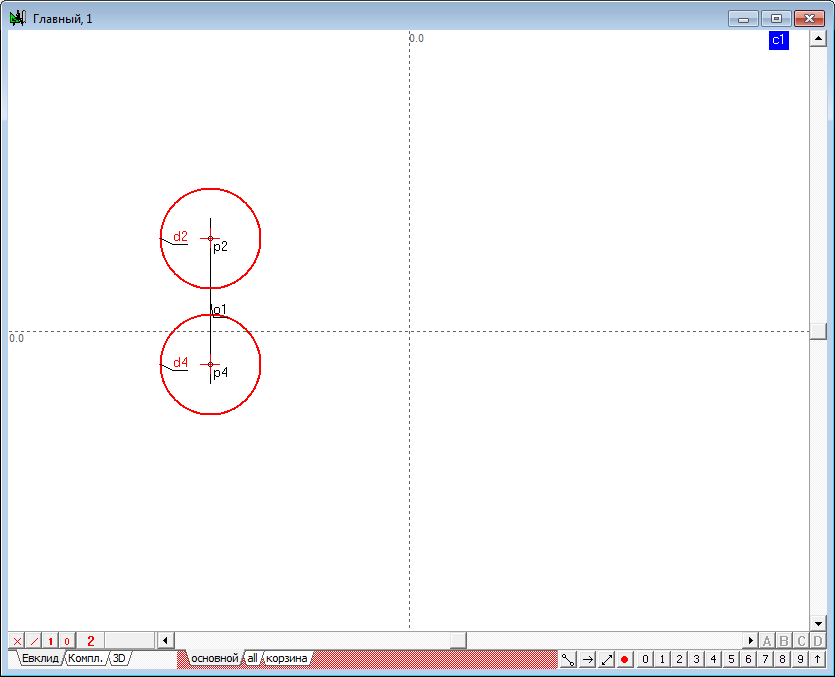
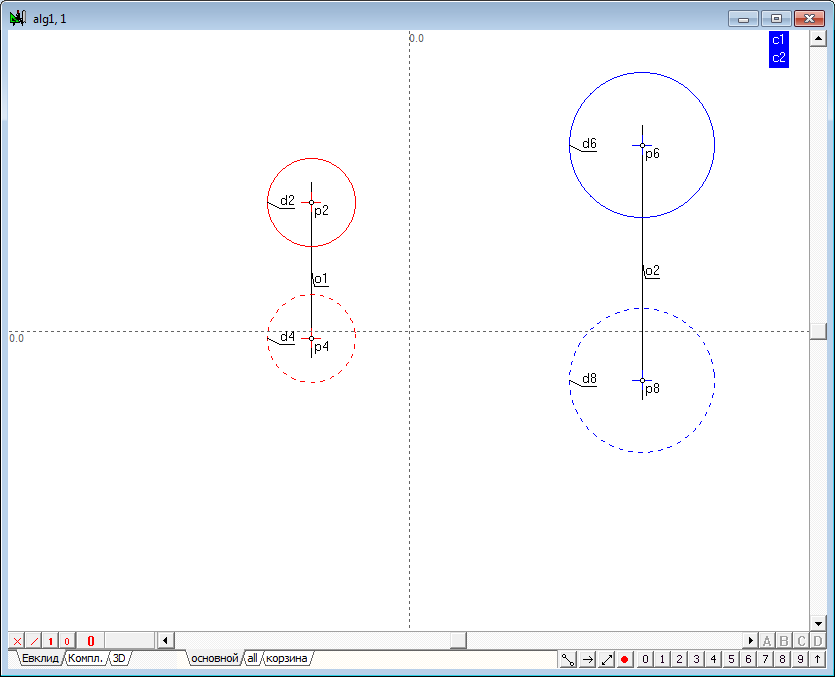
| 2 | Разместим курсор в свободном месте экрана и, нажав клавишу Ctrl, растянем окружность требуемого размера. После отпускания левой кнопки мыши в окне сформируется модель сферы, состоящая из двух окружностей, центры которых находятся на единой линии связи. Радиусы обеих окружностей взаимосвязаны посредством общей величины радиуса, заданной переменной c1. Вследствие этого, радиусом сферы можно управлять посредством шейпера, захватывая им любую из сформированных окружностей, при этом радиус оставшейся окружности будет изменяться в соответствии с изменением радиуса окружности, на которую осуществляется воздействия. | ||
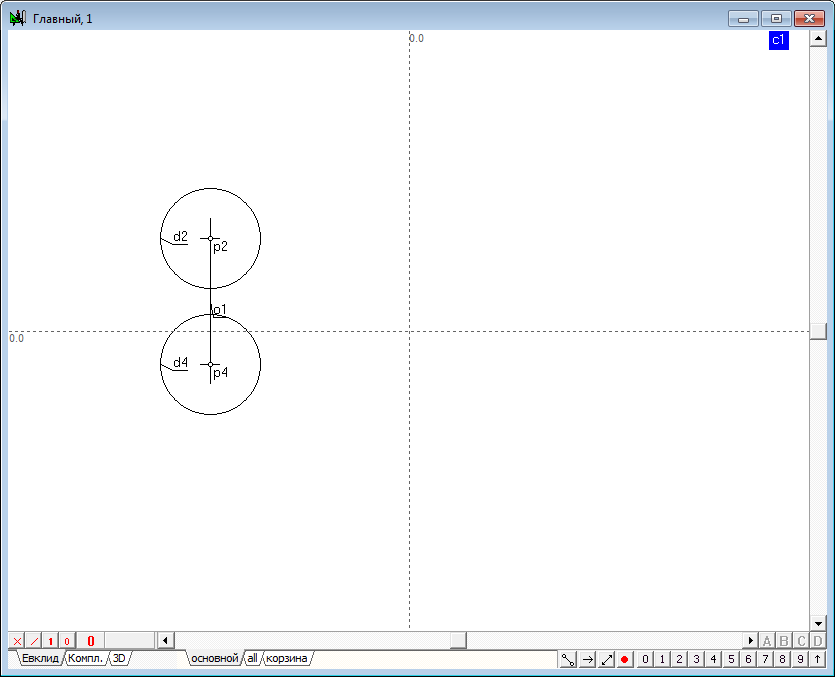 |
|||
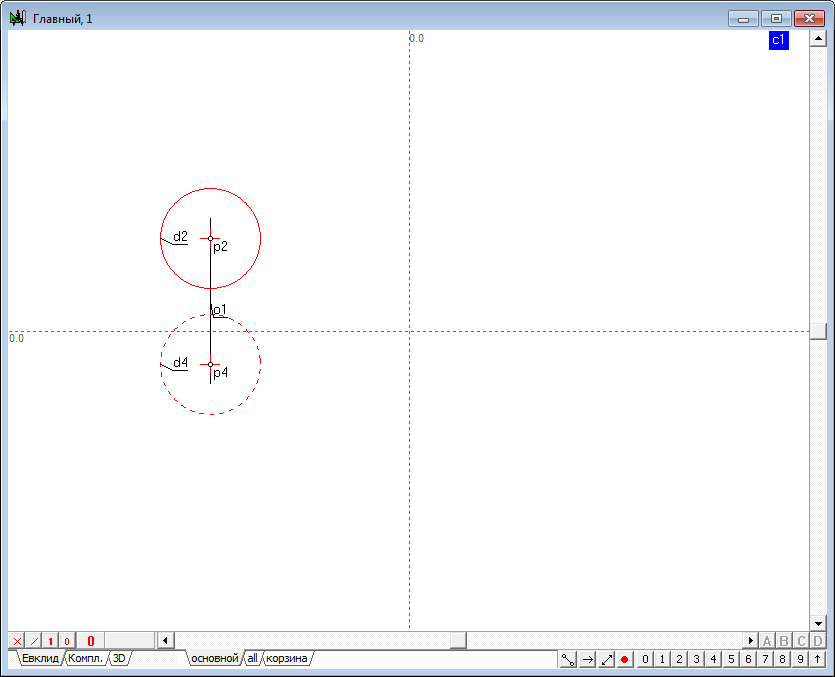
| 3 | После формирования модели имеет смысл назначить линиям цвет, который позволит отличать ее от иных моделей, присутствующих в чертеже. Для этого следует выделить обе окружности и выбрать для них общий цвет.
Для того чтобы определить различие проекций модели окружность, которую предполагается рассматривать как горизонтальную проекцию, следует изобразить иным начертанием в сравнении с фронтальной проекцией. Для этого ее следует выделить и назначить ей какое-либо начертание, например, штриховое.
|
||
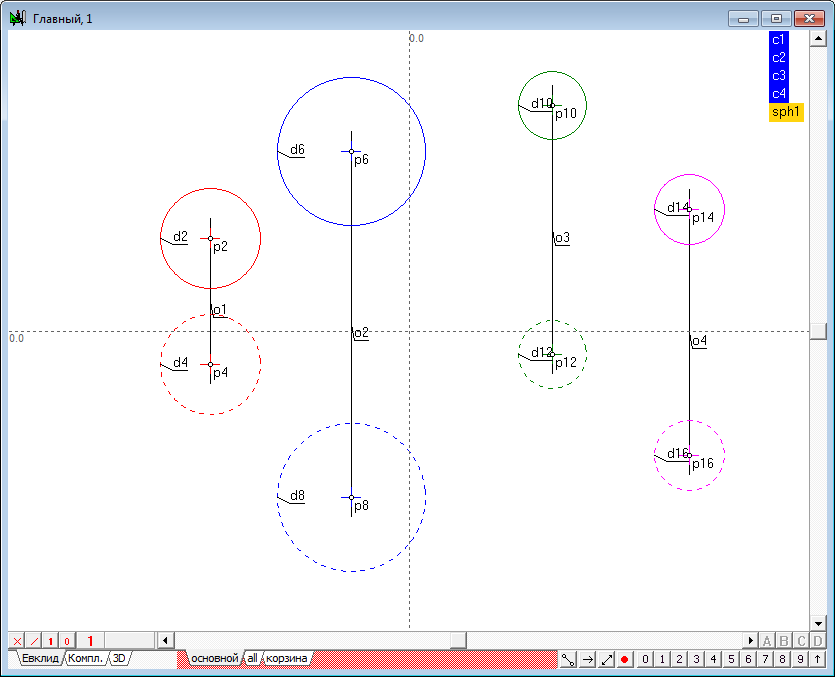
| 4 | Аналогичным образом зададим модели еще трех сфер и изменим значения атрибутов этих моделей по предложенной ранее схеме. | ||
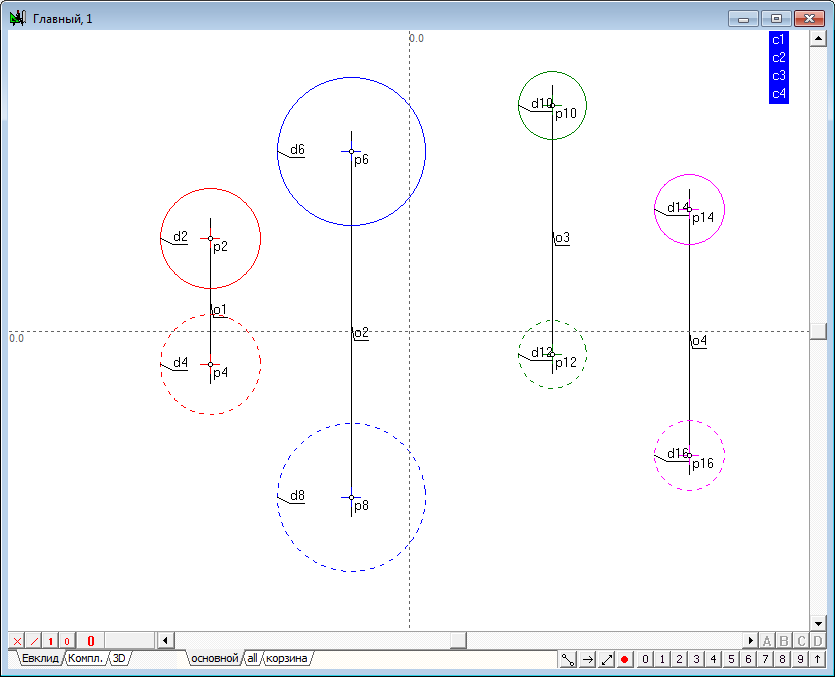 |
|||
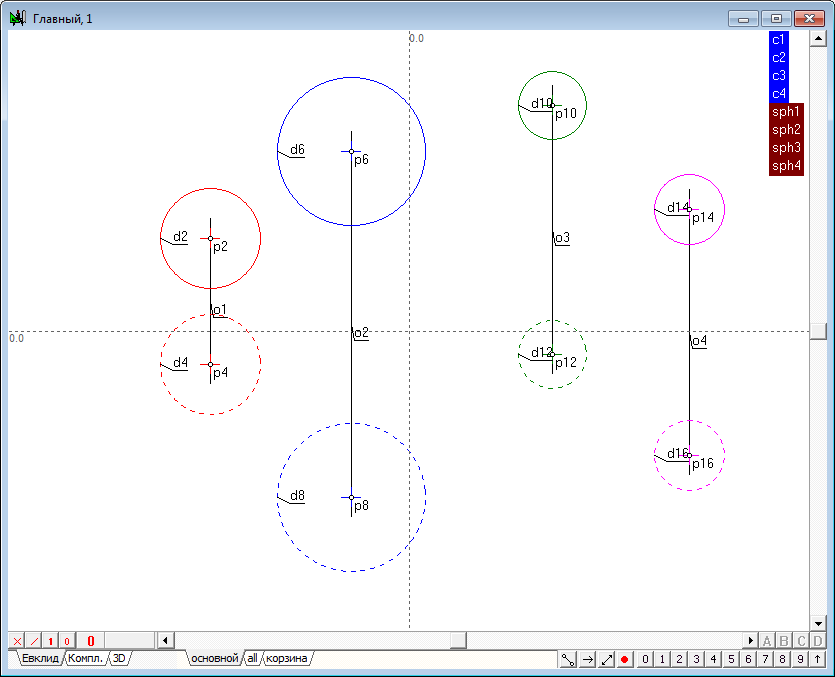
| 5 | Для облегчения будущей работы будет полезным осуществить смысловое группирование объектов моделей, позволяющая понимать под разрозненными геометрическими образами именованную совокупность, моделирующую единый объект трехмерного пространства. Выделим последовательно первую и вторую проекции первой сферы (порядок важен!), удерживая нажатой клавишу Shift, и нажмем на клавиатуре клавишу с заглавной латинской буквой G. Данная команда предназначена для присвоения имени группе выделенных объектов. В появившемся на экране окне следует указать имя этой группы, например, sph1.
Аналогичные группы следует создать для всех остальных сфер.
|
||
| 6 | Построим радикальную плоскость двух сфер. Реализуем решение задачи в новом окне, для чего создадим новый алгоритм, нажав комбинацию клавиш Ctrl+Alt+N. В новом окне, так же как и в окне главного алгоритма, построим модели двух произвольных сфер.
Идея алгоритма состоит в следующем. Пусть имеются две окружности. Соединим их центры и построим радикальную ось. Понятно, что радикальная ось будет перпендикулярной по отношению к линии, соединяющей центры исходных окружностей. Поместим эту плоскую схему в трехмерное пространство и осуществим ее вращение на 180 градусов вокруг линии-оси, соединяющей центры окружностей. При данном вращении ось переходит сама в себя, в то время как окружности образуют две сферы. Радикальная ось, вращаясь в пространстве, задаст плоскость, которая и будет радикальной плоскостью для двух образованных сфер. Следовательно, пространственную задачу можно свести к плоской, если преобразовать исходные проекции таким образом, чтобы радикальная плоскость заняла бы проецирующее положение. Такое преобразование нетрудно осуществить, если линию, соединяющую центры двух сфер, преобразовать в линию уровня в новой системе проекций. В таком случае плоскость, перпендикулярная к этой линии, будет изображаться в виде прямой линии в том поле проекций, где линия уровня изображается в натуральную величину. В этом поле проекций радикальную плоскость можно построить как радикальную ось двух окружностей при помощи стандартной функции системы Симплекс. Найдя точку пересечения этой плоскости с линией, соединяющей центры сфер, в этом поле, не составляет труда определить положение проекций этой точки в исходных полях, восстановив линии связи от известной проекции из дополнительного поля в исходные поля проекций. Теперь через полученную точку следует провести плоскость, перпендикулярную линии, соединяющей центры исходных сфер. Известно, что такая плоскость может быть легко задана при помощи двух линий уровня - фронтали и горизонтали, которые пройдут через найденную точку, причем те проекции линий уровня, которые изображаются в натуральную величину должны быть проведены перпендикулярно соответственным проекциям линии, соединяющим проекции центров исходных сфер. Построенные линии задают определитель искомой плоскости. |
||
| 7 | Начнем реализацию алгоритма. Сначала определим положение точек центров исходных сфер. Несмотря на то, что точки соответственных центров уже существуют на чертеже, они не могут быть использованы для построения алгоритма. Это объясняется тем, что точки являются предшественниками окружностей, а не наоборот. В тот момент времени, когда к алгоритму будут применены входные объекты, замещающие собой формальные объекты-параметры, их значения не смогут оказать влияние на объекты-предшественники соответственно, точки, задающие центры окружностей, не изменятся и не будут соответствовать реальному положению центров изменившихся окружностей, отображающих очерки сфер. Поэтому нам необходимо реконструировать точки центров сфер таким образом, чтобы они стали зависимыми от объектов-окружностей и позволили бы оказать влияние на оставшуюся часть алгоритма.
|
||
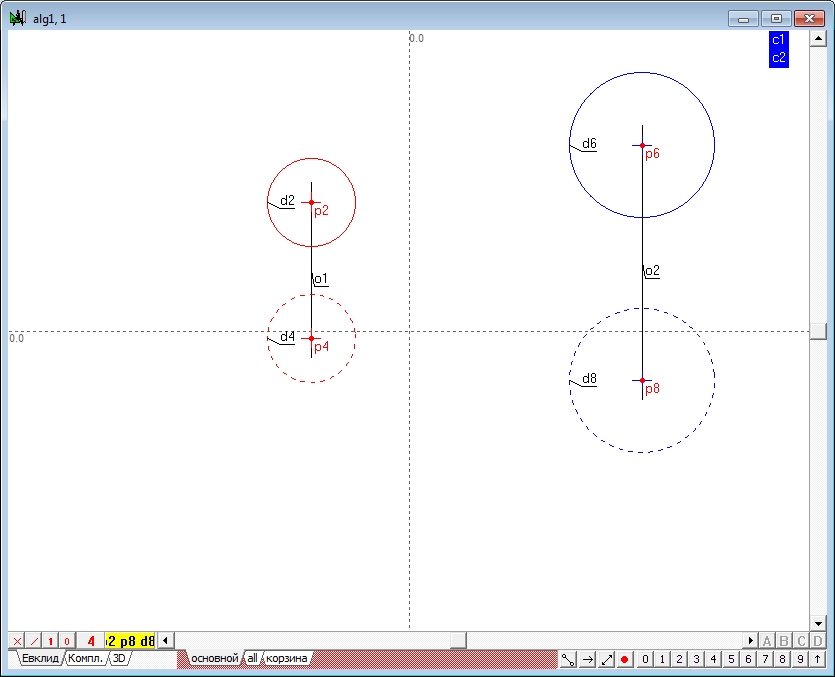
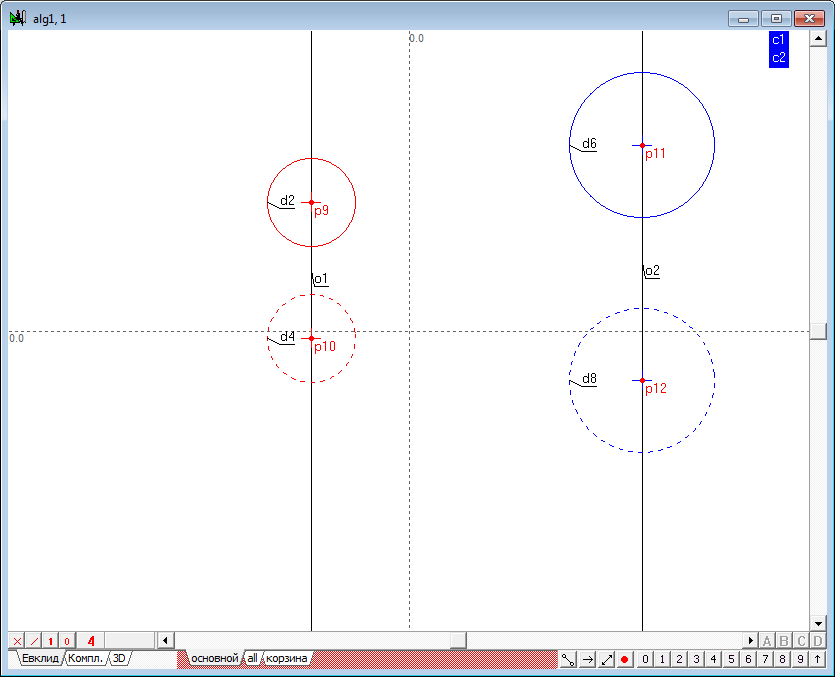
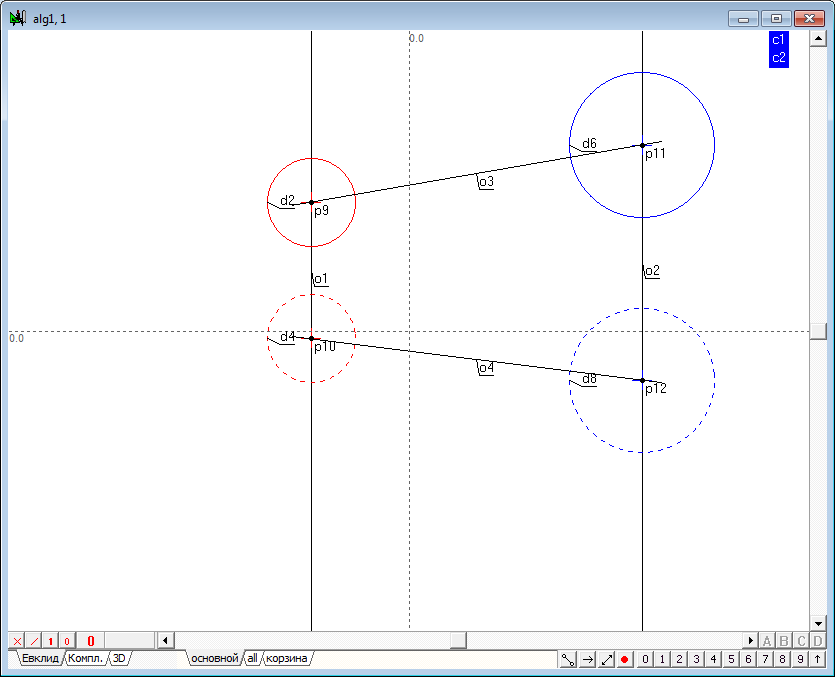
| 8 | Удерживая клавишу Shift, выделим последовательно окружности d2, d4, d6, d8 и нажмем на клавиатуре клавишу с латинским символом c. Это действие позволит образовать точки центров, зависимые от соответственных окружностей.
|
||
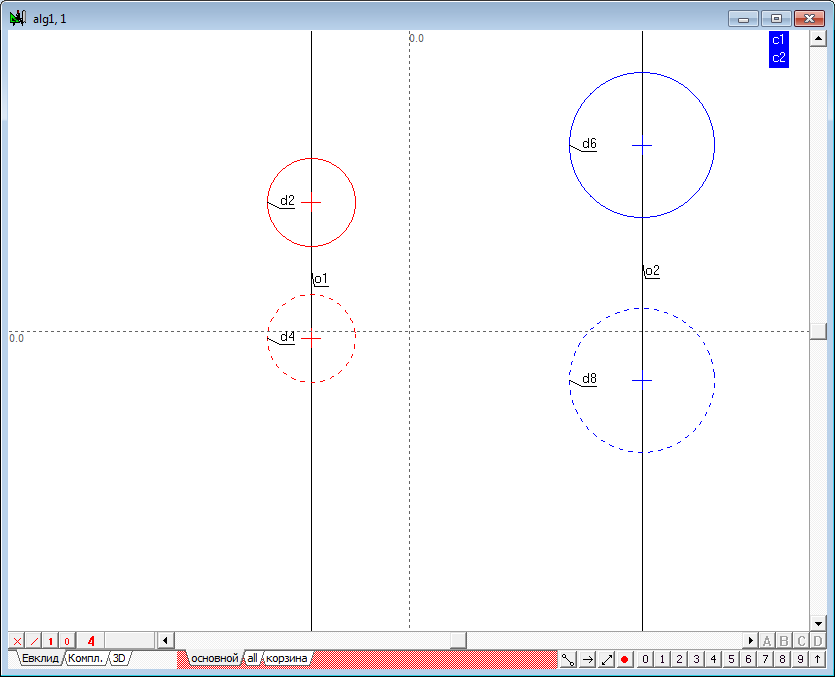
| 9 | Соединим соответственные проекции центров прямыми линиями и назначим им атрибут беконечности.
|
||
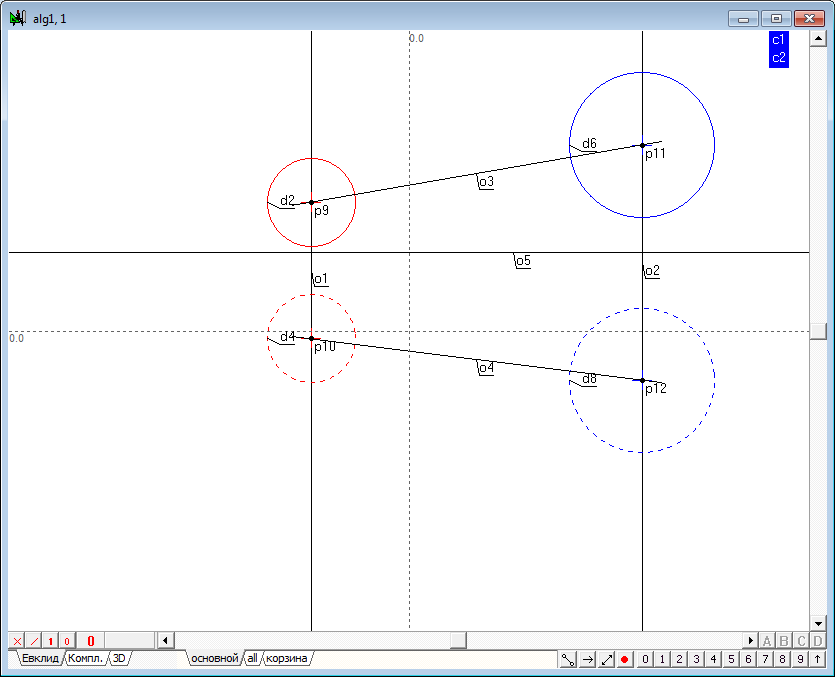
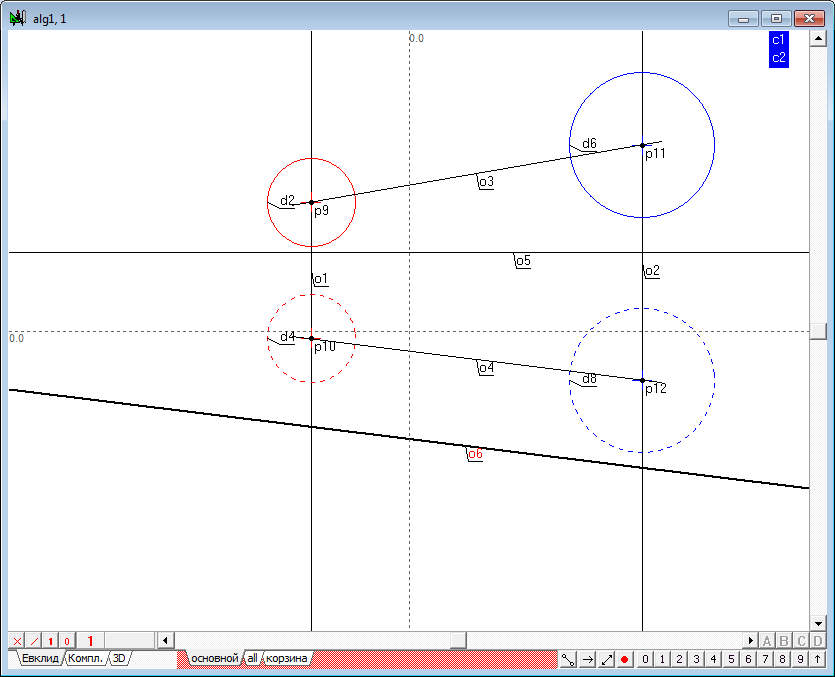
| 10 | Для построения дополнительного поля проекций определим ось проекций в исходных полях как произвольную горизонтальную прямую. Для выполнения этой операции разместим курсор в произвольном месте экрана и нажмем на клавиатуре клавишу с латинским символом h.
Ось, определяющая дополнительное поле проекций, должна быть определена как параллельная прямая к одной из проекций линии, соединяющей соответственные проекции центров сфер. Для выполнения этой операции выделим, например, прямую o4, отведем курсор на некоторое расстояние от этой прямой и нажмем на клавиатуре клавишу с латинским символом o. Эта команда позволит задать требуемую линию. При необходимости положение прямой можно откорректировать шейпером.
|
||
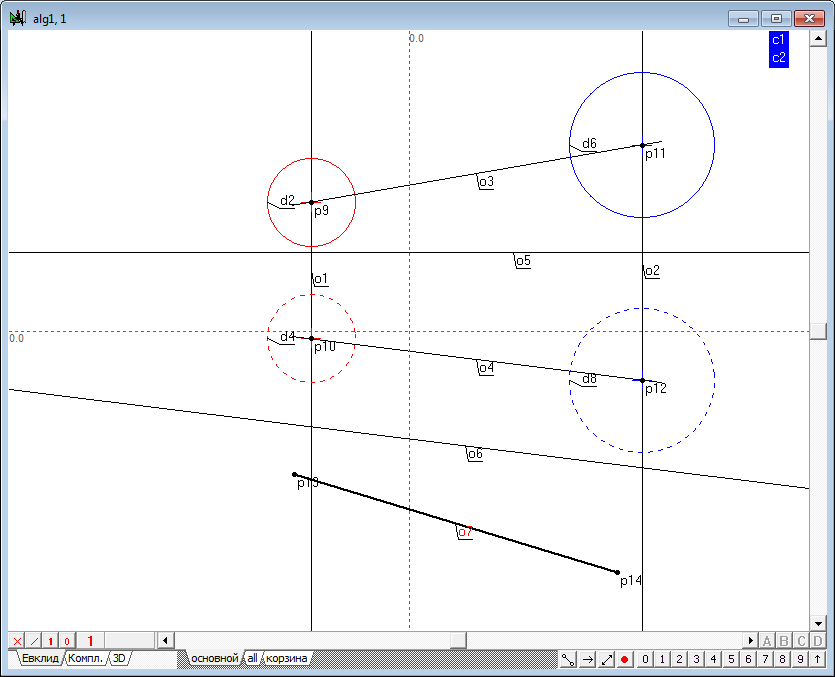
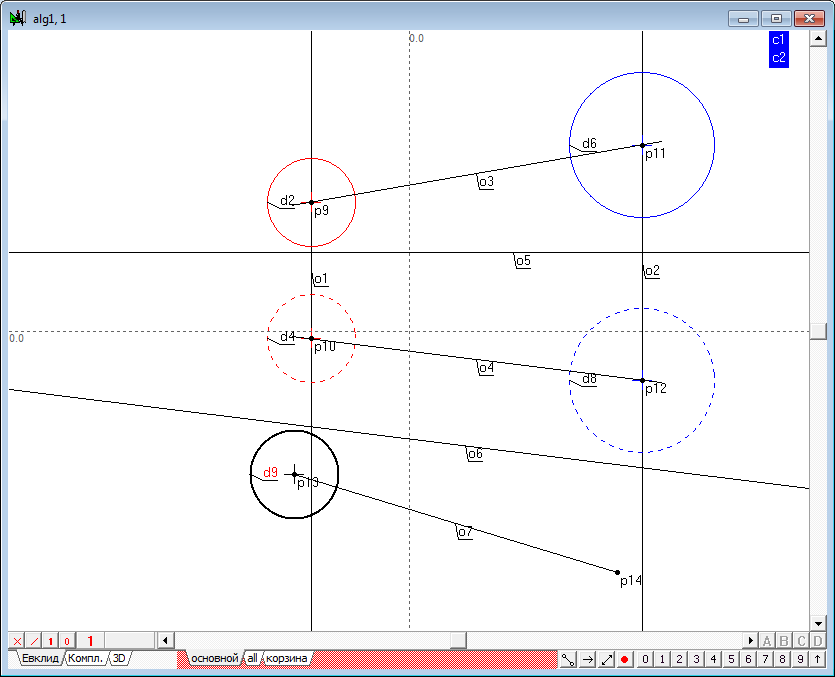
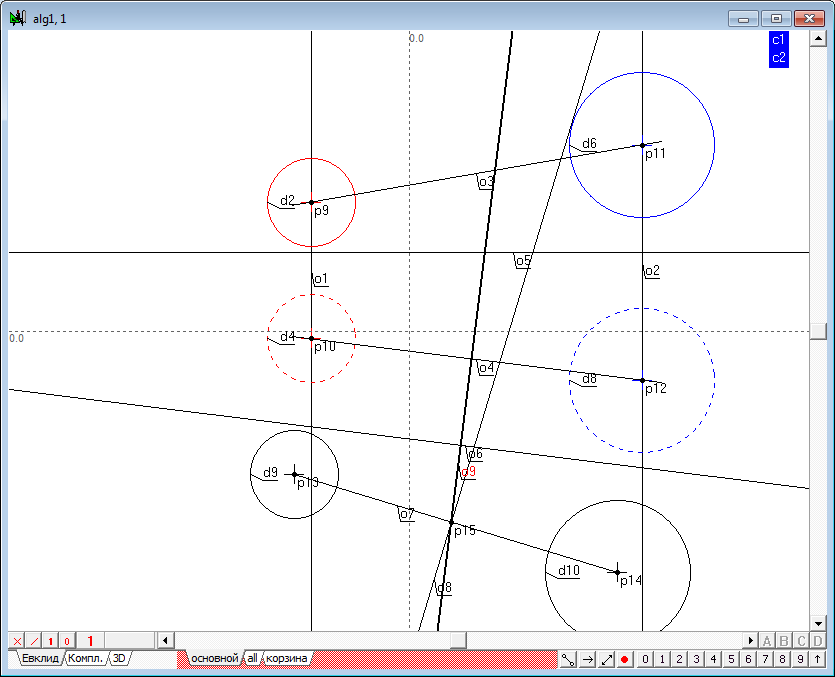
| 11 | Теперь построим дополнительную проекцию центров сфер. Дважды выполним преобразование, используя для этого функцию замены плоскостей проекций. В результате получим две точки (p13, p14), через которые проведем прямую линию o7.
Прямые o4 и o7 моделируют линию уровня в новой системе плоскостей проекций, причем прямая o7 изображает линию соединения центров сфер в натуральную величину. Следовательно, в этом поле радикальная плоскость, которая является перпендикулярной в отношении к линии соединения центров сфер, является проецирующей в этом поле и изображается радикальной осью двух окружностей d9 и d10, которые предстоит построить. |
||
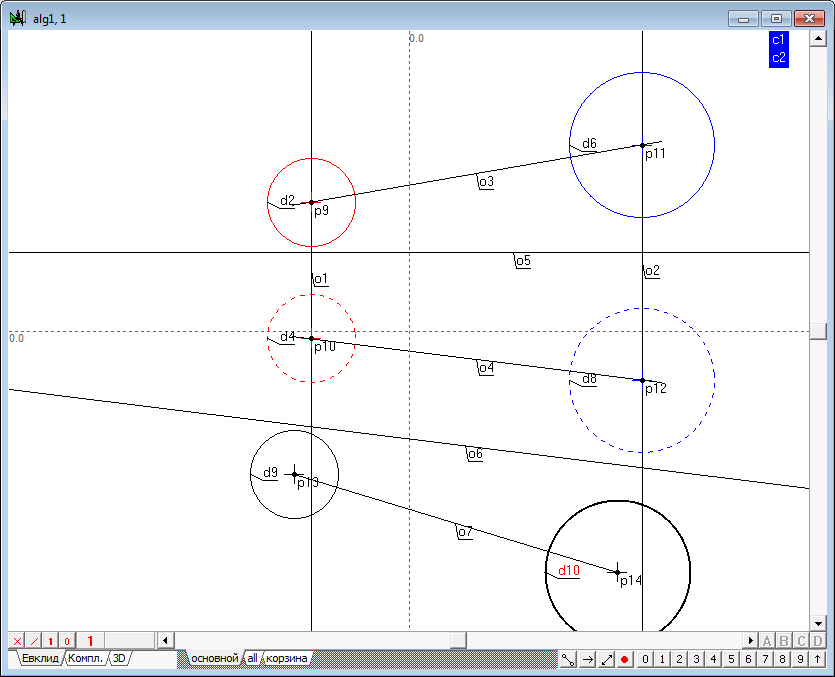
| 12 | Построим очерки сфер в третьем поле. Для этого, удерживая нажатой клавишу Shift, выделим последовательно точку p13 и окружность d4, затем нажмем на клавиатуре клавишу с латинским символом d. Третья проекция очерка сферы (окружность d9) будет построена.
Аналогично построим второй очерк сферы.
|
||
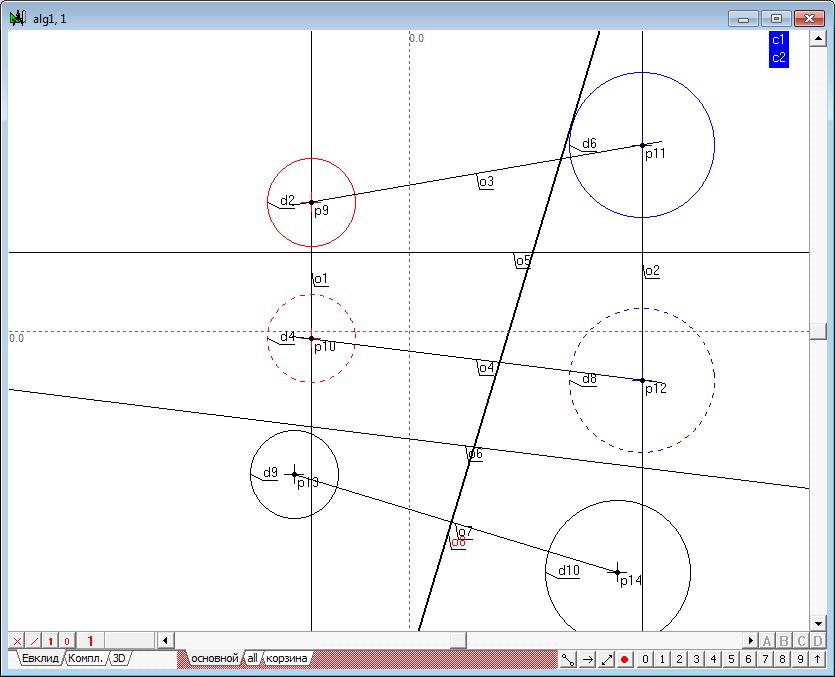
| 13 | Удерживая нажатой клавишу Shift, выделим последовательно окружности d9 и d10. Нажмем клавишу с латинским символом r, и постройте радикальную ось двух окружностей - линию o8.
|
||
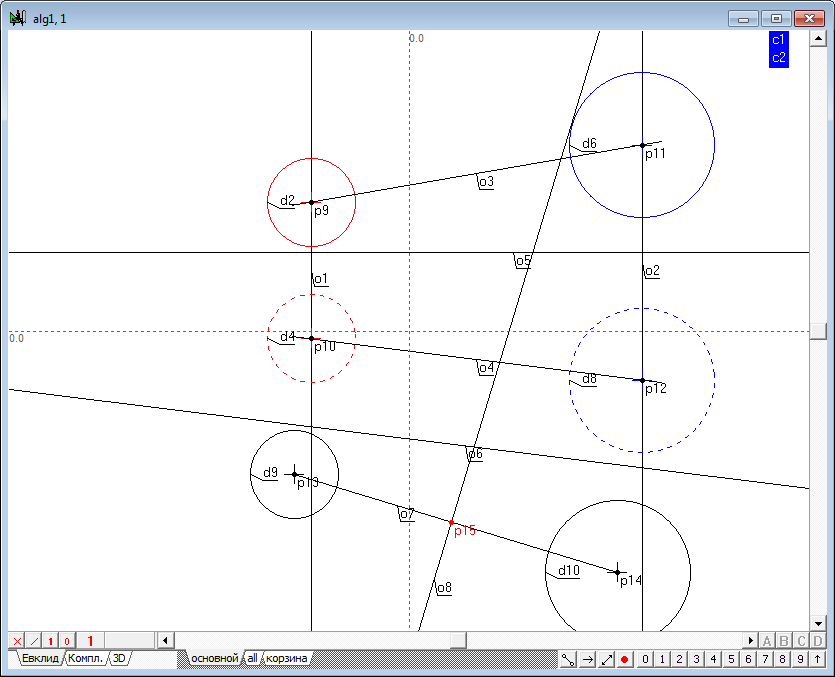
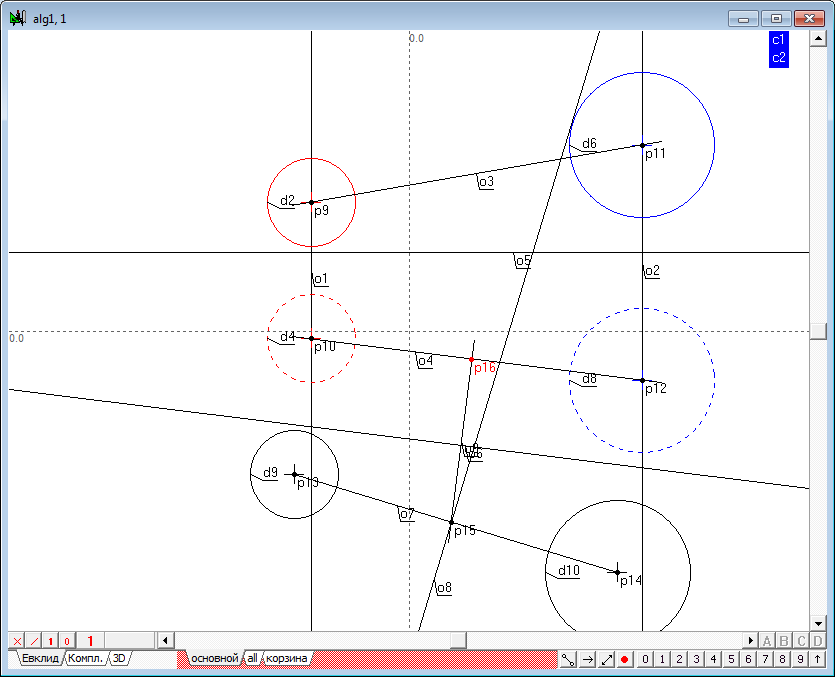
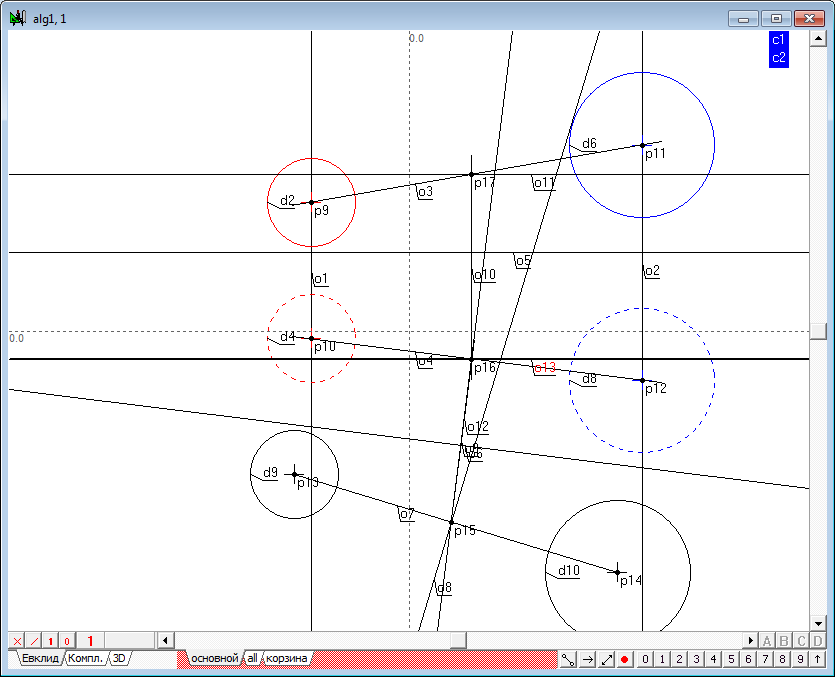
| 14 | Теперь определим пересечение радикальной оси o8 с линией, соединяющей проекции центров исходных сфер - точку p15.
Поскольку точка пересечения радикальной плоскости с прямой, соединяющей центры сфер, принадлежит этой прямой, то между проекциями этой точки на чертеже должно соблюдаться проекционное соответствие и принцип сохранения инцидетности. Поэтому для построения второй проекции точки, удерживая нажатой клавишу Shift, выделим последовательно точку p15 и прямую линию o6, а затем нажмем на клавиатуре клавишу с латинским символом o. В результате будет построена линия связи между третьим (дополнительным) и вторым полем проекций - прямая o9.
Вторая проекция точки пересечения радикальной плоскости с прямой, соединяющей центры сфер (p16), определяется, как точка пересечения прямых линий o9 и o4.
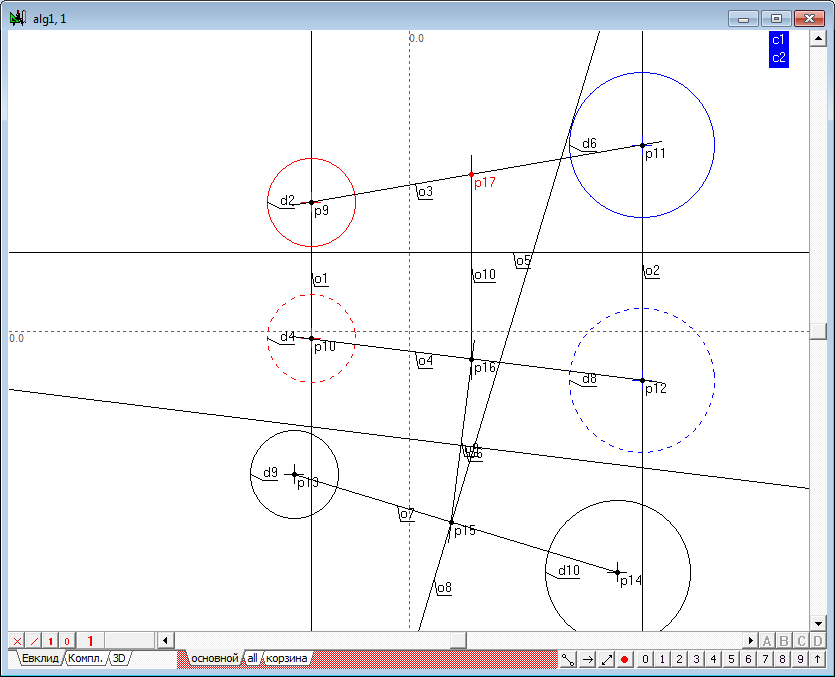
Восстановим линию связи из второго поля в первое. Для этого (при уже выделенной точке p16) нажмем на клавиатуре клавишу с латинским символом v, построим прямую o10 и пересечем ее с первой проекцией прямой (o3), соединяющей первые проекции центров исходных сфер. Следовательно, при наличии первой и второй проекций (o3 и o4) пространственное положение прямой линии, соединяющей центры исходных сфер, определено.
|
||
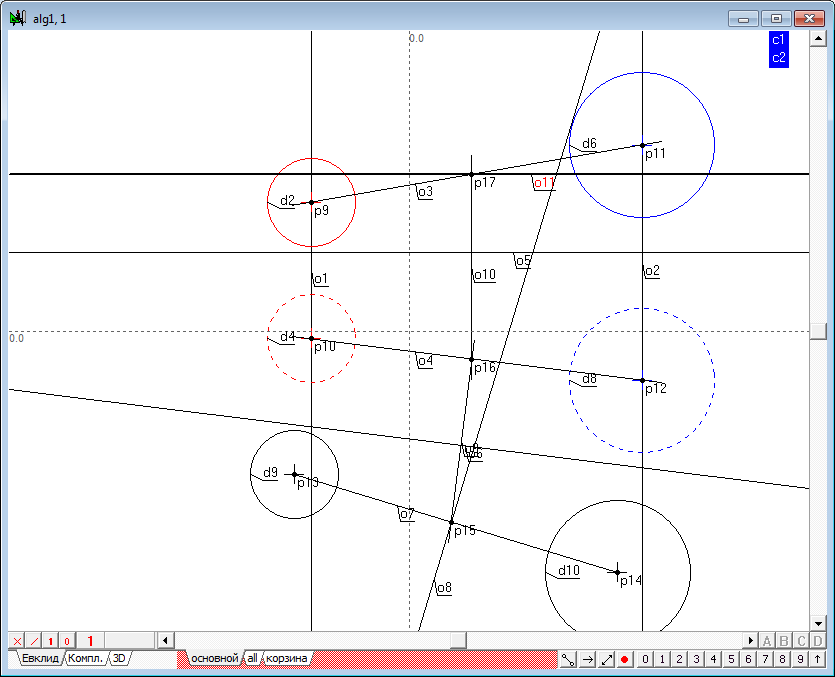
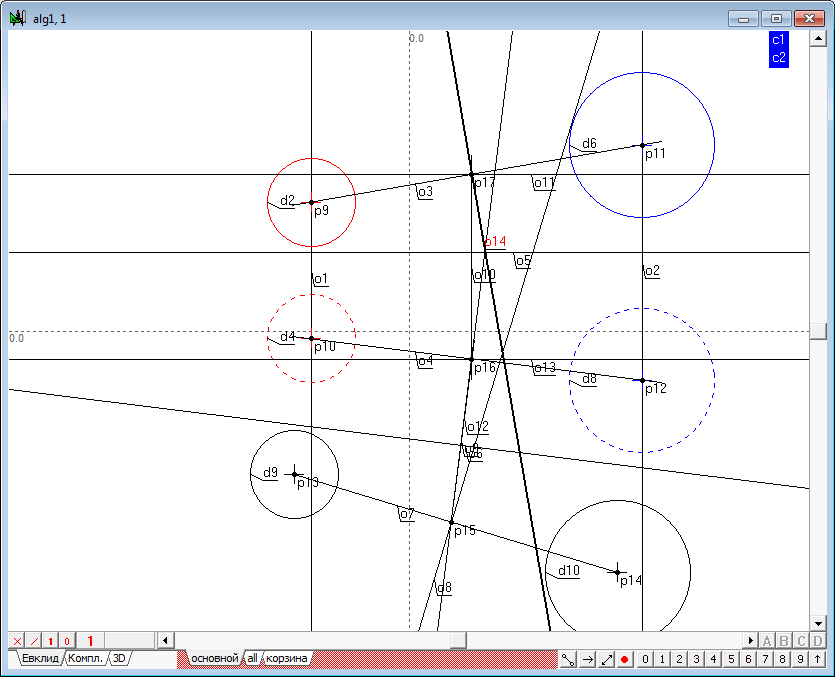
| 15 | Теперь мы должны через найденную точку провести перпендикулярную плоскость. Наиболее удобный способ задать эту плоскость - это провести через точку две линии: фронталь и горизонталь. Для построения горизонтали в плоскости, выделим точку p17 и нажмем на клавиатуре клавишу с латинским символом h. Получим прямую o11.
Затем, удерживая нажатой клавишу Shift, выделим последовательно точку p16 и прямую линию o4, а затем нажмем на клавиатуре клавишу с латинским символом o. Получим линию o12. Прямые o11 и o12 моделируют одну из прямых плоскости, перпендикулярную к заданной прямой (o3, o4) - горизонталь.
Для построения фронтали в плоскости, выделим точку p16 и нажмем на клавиатуре клавишу с латинским символом h. Получим прямую o13.
Теперь, удерживая нажатой клавишу Shift, выделим точку p17 и прямую o3, затем нажмем на клавиатуре клавишу с латинским символом o. Получим прямую o14.
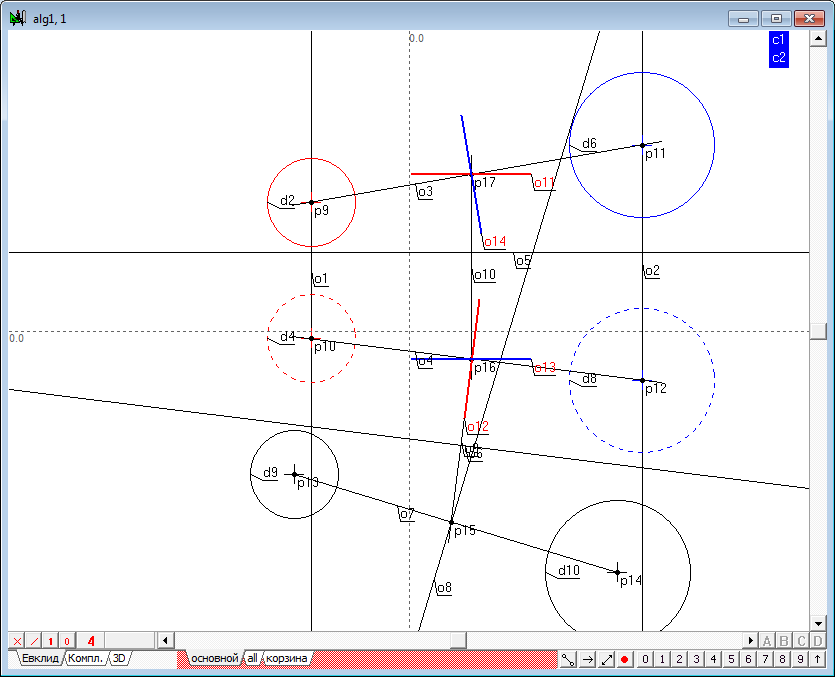
Прямые o13 и o14 моделируют вторую линию плоскости, перпендикулярную к заданной прямой. Поскольку мы имеем две пересекающиеся прямые линии, то плоскость, перпендикулярная к исходной прямой, задана. Радикальная плоскость определена. Для удобства использования выходных параметров алгоритма при внешних обращениях к нему из других алгоритмах, назначим полученным линиям радикальной плоскости соответственные цвета, которые позволят легко отличать первую прямую от второй. Помимо этого целесообразно линиям разных проекции назначить различные атрибуты начертаний (например, у первой проекции оставить сплошное начертание, а для второй назначить начертание штриховое). Кроме того, имеет смысл ограничить размер отображения линии, что можно сделать, выделив линии и изменить их атрибут отображения нажатием на клавишу с цифрой 9. Это позволит существенно повысить различимость объектов, моделируемых линиями, в вызывающем алгоритме, в котором, в принципе, может образовываться большое количество таких объектов..
|
||
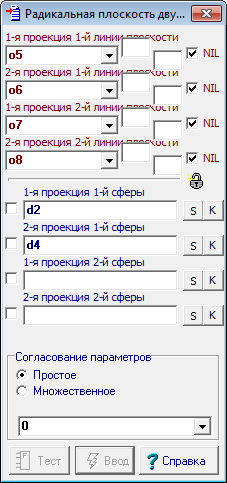
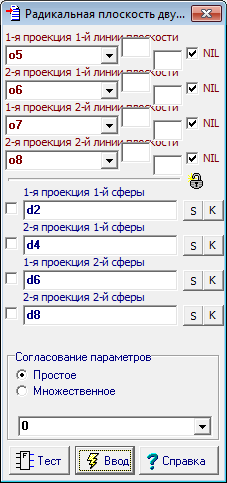
| 16 | Оформим интерфейс созданного алгоритм. Удерживая нажатой клавишу Shift, выделим последовательно первую и вторую проекцию очерков первой сферы (окружности d2 и d4), а затем первую и вторую проекцию очерков второй сферы - окружности d6 и d8. Правой кнопкой мыши вызовем контекстное меню, выберем пункт - Назначить "d2,d4,d6,d8" входом алгоритма. В поле ввода диалоговых окон, которые будут затем последовательно появляться на экране, внесем текст, поясняющий смысл назначенных входных параметров алгоритма: 1-я проекция 1-й сферы; Теперь выделим последовательно первую и вторую проекции первой прямой радикальной плоскости - прямые o11 и o12, и затем первую и вторую проекции второй прямой радикальной плоскости - прямые 14 и o13. Правой кнопкой мыши вызовем контекстное меню, выберем пункт - Назначить "o11, o12, o14, o13" выходом алгоритма. В поле ввода диалоговых окон, которые будут затем последовательно появляться на экране, внесем текст, поясняющий смысл назначенных выходных параметров алгоритма: 1-я проекция 1-й линии плоскости; Мы должны дать осмысленное название алгоритму. Откроем диалоговое окно, предназначенное для создания интерфейса алгоритма, нажатием комбинации клавиш Alt+A. В поле ввода названия алгоритм введем текст: Радикальная плоскость двух сфер. |
||
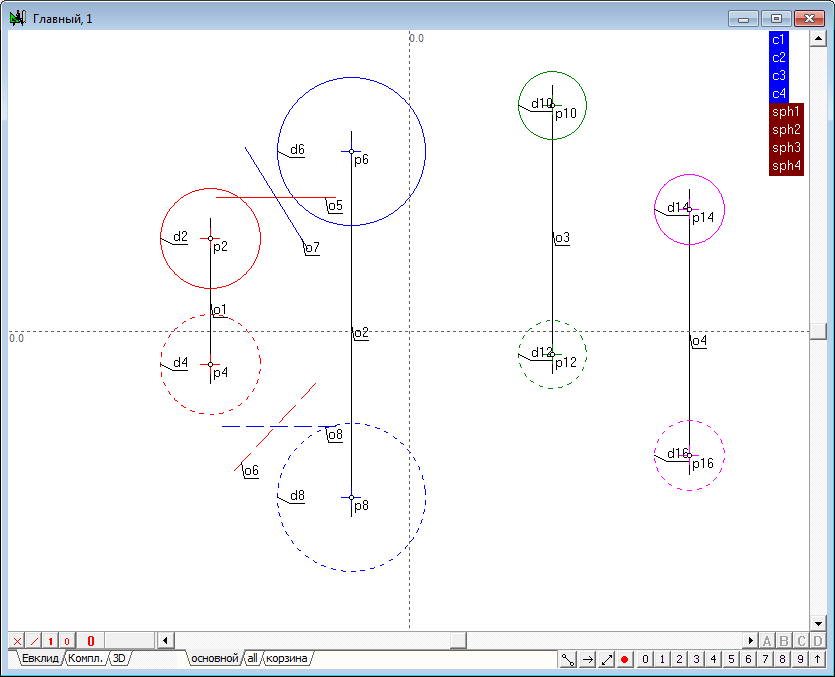
| 17 | Настал момент для построения радикальных осей трех пар сфер, представленных в виде групп: sph1-sph2; sph1-sph3; sph1-sph4. Перейдем в Главный алгоритм, щелкнув левой кнопкой мыши над окном главного алгоритма, выберем пункт Отношения/Процедуры/Радикальная ось двух сфер... Диалоговое окно, которое появится при этом на экране, будет содержать четыре поля для ввода параметров сформированной нами функции. Разумеется, мы можем осуществить ввод фактических параметров в алгоритм, указывая последовательно на все соответственные объекты в чертеже. Однако формирование перечня параметров можно ускорить (и упростить), если ссылаться при помощи мыши на метки имен соответственных групп. Укажем, например, на имя группы sph1. При этом имена объектов, входящих в группу, будут подставлены последовательно в поля диалоговой панели, формирующей обращение к функции построения радикальной плоскости со ссылкой на первую сферу.
Нажатие на метку с именем группы sph2 позволит полностью сформировать входные параметры.
Здесь следует отметить, что порядок объектов в группе должен полностью соответствовать порядку следования входных параметров алгоритма. Поэтому при разработке алгоритма следует заранее позаботиться о соблюдении этого порядка при формировании групп и перечней параметров алгоритма.
|
||
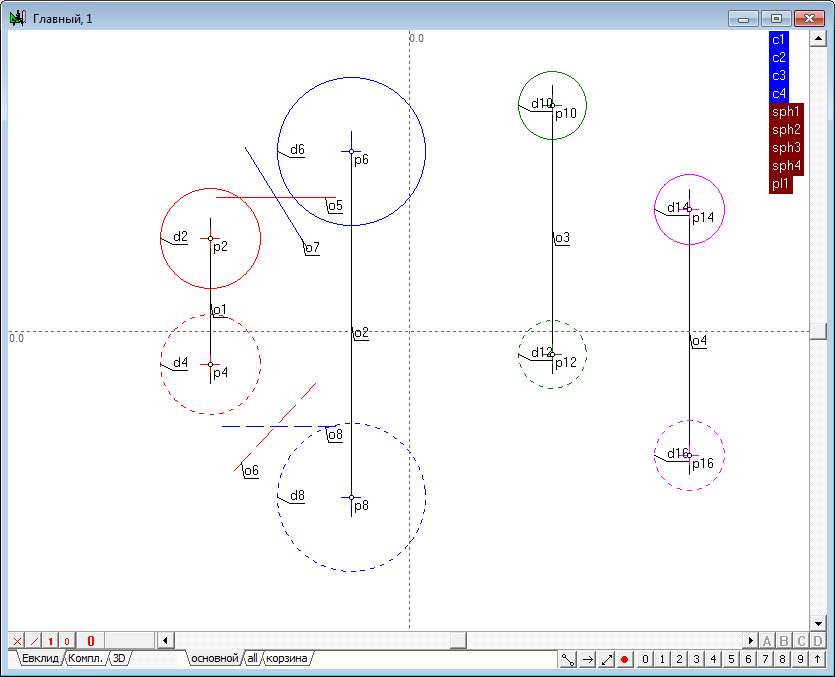
| 18 | Выполнив аналогичные действия для групп sph1-sph3; sph1-sph4, получим образы всех трех радикальных плоскостей. Назначим группы для полученных плоскостей. Выделив последовательно объекты (или, сняв выделение со всех объектов, нажмем на клавишу с латинским символом l, что приведет к выделению всех объектов, сгенерированных последней командой), моделирующие первую радикальную плоскость, нажмем на клавиатуре на клавишу с латинским символом G. Укажем имя группы, например, pl1.
Аналогично сформируем названия групп для оставшихся плоскостей - pl2 и pl3.
|
||
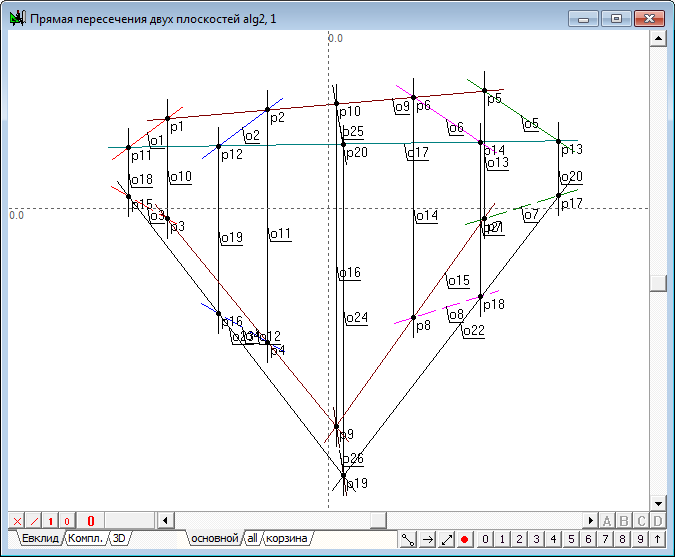
| 19 | Решение задачи построения линии пересечения двух плоскостей выполним в строгом соответствии с алгоритмом описанном в примере Пересечение плоскостей.
|
||
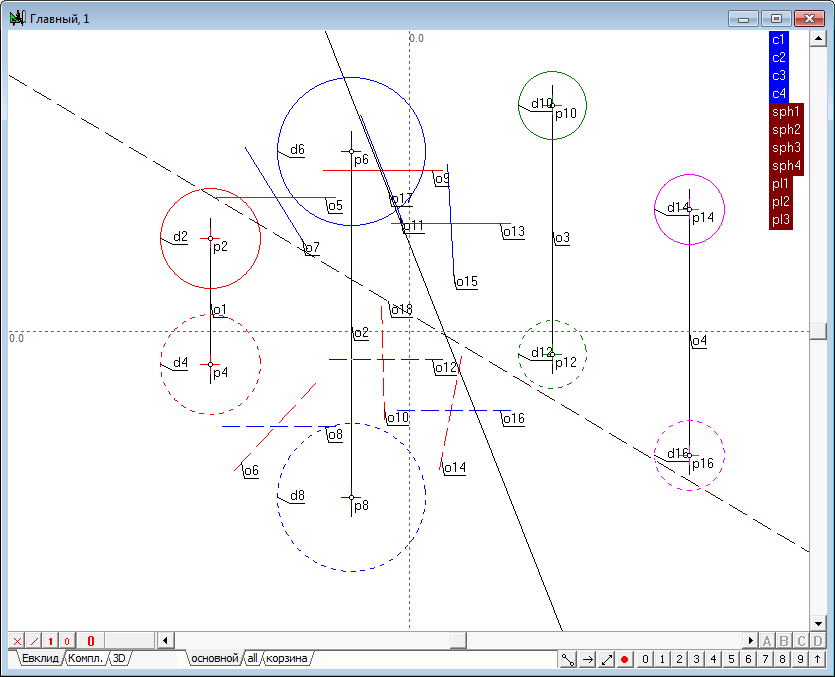
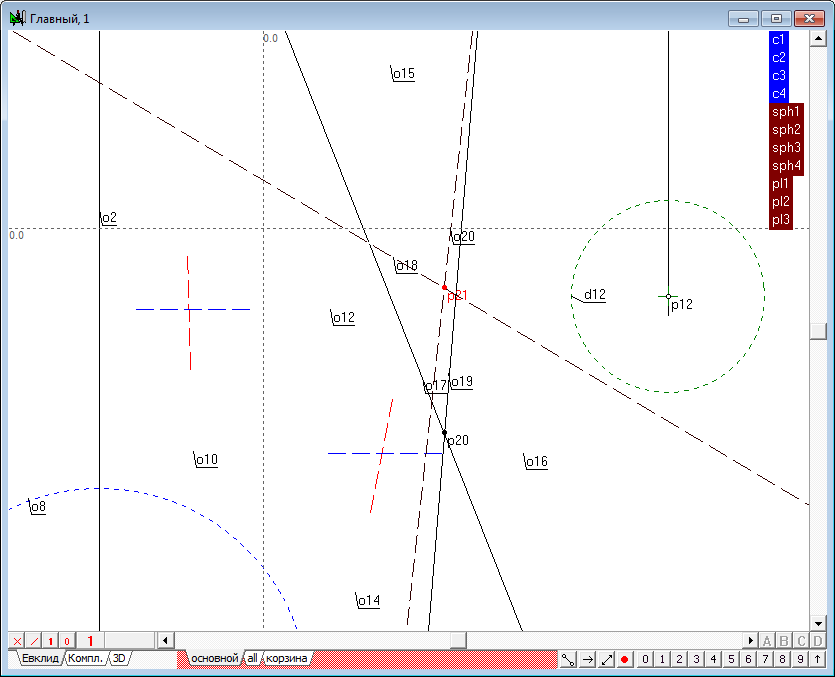
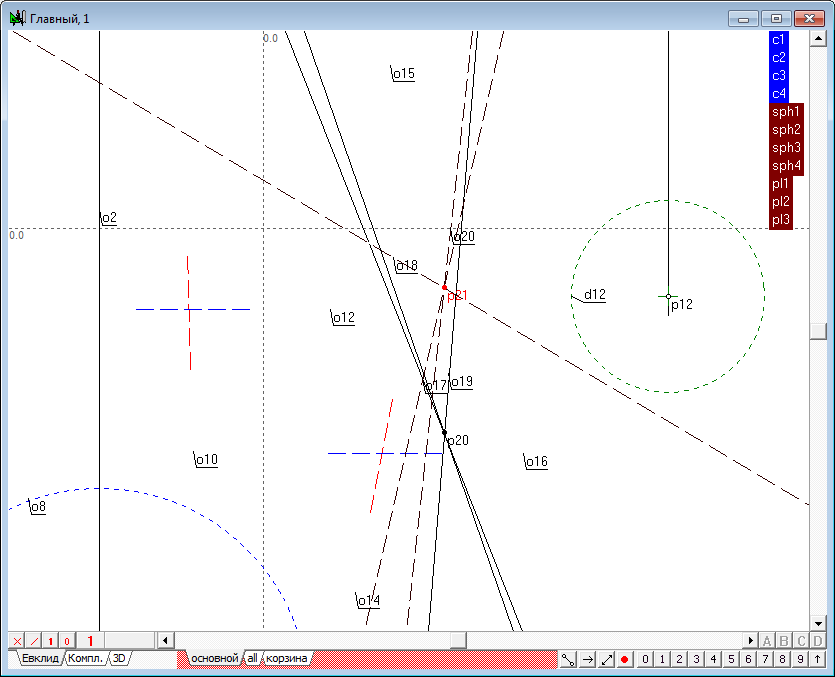
| 20 | Найдем пересечение первой и второй радикальных плоскостей (pl1-pl2). Для этого выберем пункт меню Отношения/Процедуры/Пересечение двух плоскостей... Ссылаясь на группы, соответствующие исходным плоскостям, сформируем команду и выполним ее.
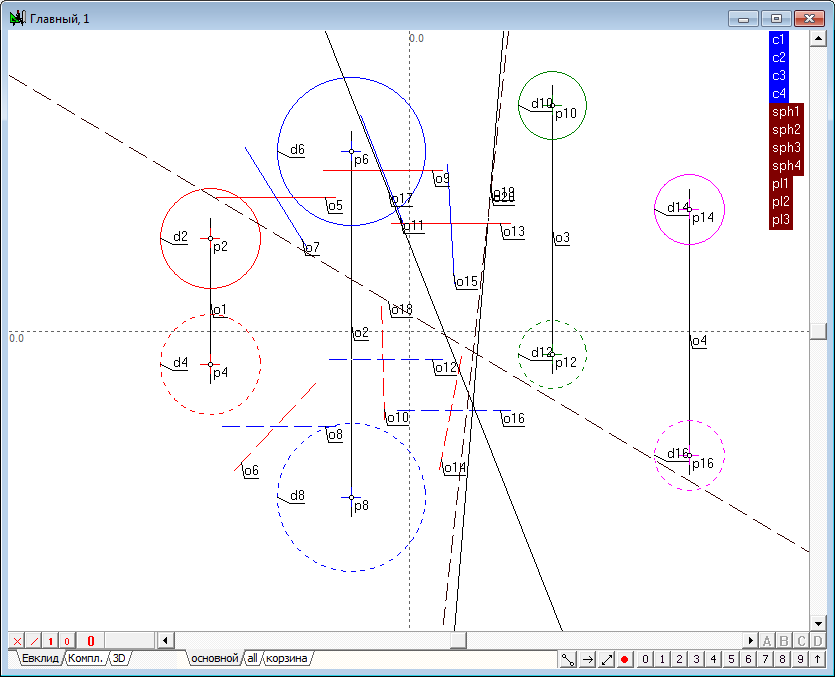
Найдем пересечение первой (pl1) и третьей (pl3) радикальных плоскостей.
Найдем точки пересечения соответственных линий в первом и втором полях проекций. Заметим, что образованные точки находятся на общей линии связи.
Несмотря на то, что решение уже получено, рекомендуется убедиться в том, что построение линии пересечения плоcкостей pl2-pl3 приведет к получению того же результата. Таким образом, геометрическое место радикального центра четырех сфер найдено.
|
||
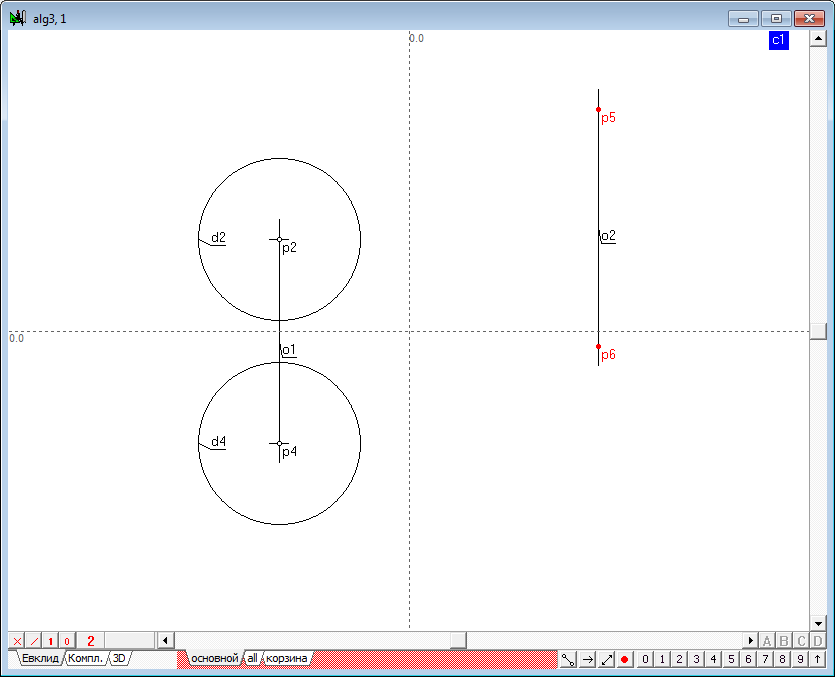
| 21 | Для завершения решения задачи нам осталось определить длину образующей конуса, опущенного из радикального центра на любую из исходных сфер. Создадим новый алгоритм и зададим в нем сферу (инструмент свободная окружность с нажатой клавишей Ctrl) и точку (при снятом выделении нажать на клавишу с латинским символом v).
|
||
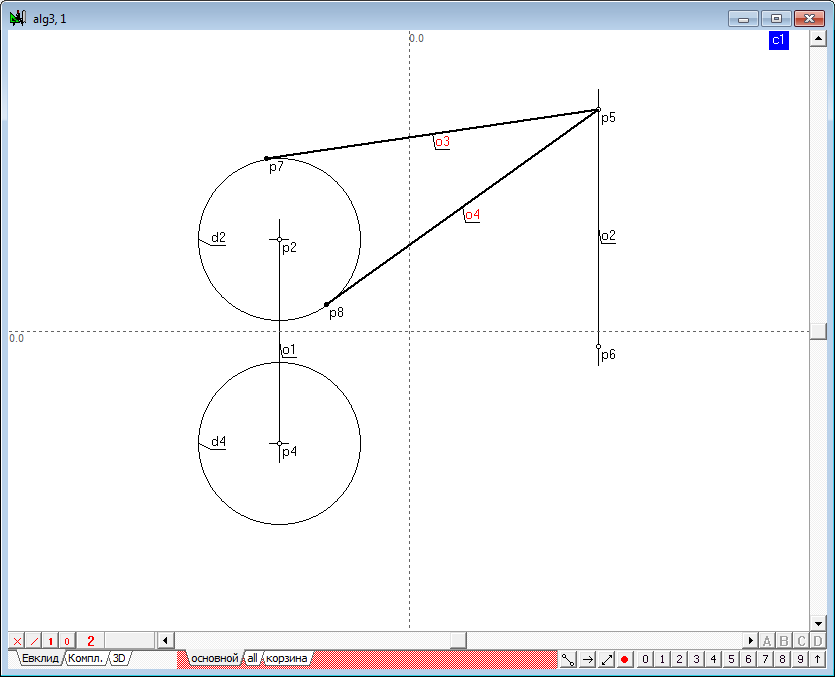
| 22 | Опустим из первой проекции точки касательные на первую проекцию очерка сферы. Для этого, удерживая нажатой клавишу Shift, выделим последовательно точку p5 и окружность d2 и нажмем на клавиатуре клавишу с латинской буквой o.
В соответствии с правилами моделирования сферы, вторую проекцию точки касания образующей, находящейся на главном меридиане, следует искать на второй проекции главного меридиана. Для того чтобы построить линию второй проекции главного меридиана, выделим точку p4 и перенесем ее в слой корзина (см. замечание о центрах сфер в задаче построения радикальной плоскости) нажатием на клавишу \, найдем центр p9 окружности d4, выделив ее и нажав клавишу с латинским символом c, а затем нажмем на клавишу с латинским символом h (линия o5). Не снимая выделения с полученной линии, удерживая нажатой клавишу Shift, добавим к выделению точку p7, после чего нажмем на клавишу с латинским символом p. Тем самым, мы получили вторую проекцию p10 точки касания образующей, опущенной из точки на сферу. Построим эту касательную и определим ее истинную величину. |
||
| 23 | Алгоритм построения истинной длины отрезка уже рассматривался нами ранее. Напомним лишь, что для решения задачи нужно задать положение оси o7 исходной системы проекций (произвольная прямая линия, определяемая нажатием на клавишу с латинским символом h) и оси o8 дополнительной системы проекций (выделяется одна из проекций (o6) измеряемой прямой и параллельно ей проводится прямая o8, путем нажатия на клавишу с латинским символом o). Затем строятся дополнительные проекции точек p11, p12, определяющих измеряемый отрезок o9. Через полученные точки проводим прямую линию o9, выделив эти точки и нажав клавишу с латинским символом o. Определение искомой длины c2 осуществляется путем нажатия на клавишу с латинским символом l. Выделив проекции очерков сферы и проекции точки, назначим их входными параметрами и укажем их названия. Единственным выходным параметром является величина c2. Назначим ее в качестве выходного параметра и присвоим ему название - Длина отрезка. Нажав на комбинацию клавиш Alt+A, вызовем панель настройки алгоритма, в которой дадим этому алгоритму название - Длина образующей конуса. |
||
| 24 | Вернувшись в главный алгоритм, найдем искомые расстояния от радикального центра до всех исходных сфер, вызвав только что сформированную функцию. Убедимся в том, что все найденные расстояния одинаковы.
Для этого следует вызвать протокол значений объектов комбинацией клавиш Alt+O, и выбрать соответственные переменные. |
||
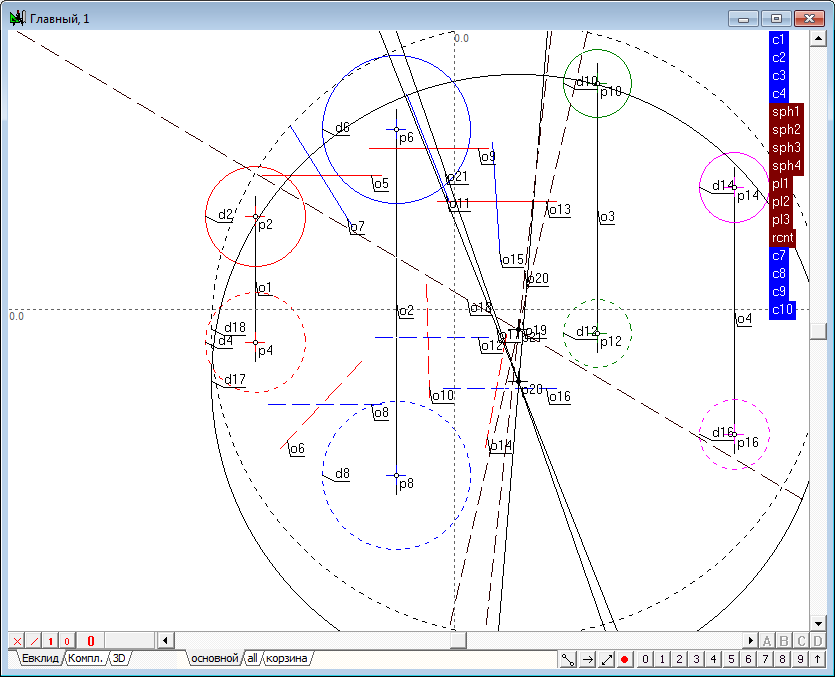
| 25 | Завершим решение задачи, выделив первую проекцию радикального центра и найденную величину, после чего нажмем на клавишу с латинским символом d. На экране будет построена первая проекция сферы, ортогональной к четырем заданным сферам. Вторую проекцию построим, выделив точку p19 и величину c7. Воспользуемся той же командой для построения второй проекции очерка сферы. Изменим начертание второй проекции на штриховое.
|
||
| 26 | Таким образом, нами получен алгоритм построения сферы, ортогональной к четырем заданным. Имеет смысл оформить этот алгоритм в виде самостоятельной процедуры, пригодной для дальнейшего исследования свойств системы четырех сфер. Выделим все объекты главного алгоритма комбинацией Ctrl+A и скопируем их в Clipboard соответственным пунктом меню. Подтвердим, что копируются все объекты алгоритма. Создадим новый алгоритм комбинацией клавиш Ctrl+Alt+N и вставим в него содержимое буфера Clipboard. В появившемся диалоговом окне выберем режим Обыкновенная вставка. |
||
| 27 | Оформим интерфейс алгоритма. Выделим последовательно первую и вторую проекции очерка первой сферы, затем второй, третьей и четвертой. Назначим выделенные объекты входными параметрами алгоритма. В качестве выходных параметров укажем первую и вторую проекцию ортогональной сферы. В окне настройки интерфейса алгоритма укажем названия входных и выходным параметров и самого алгоритма, например, Ортогональная сфера к четырем сферам. | ||
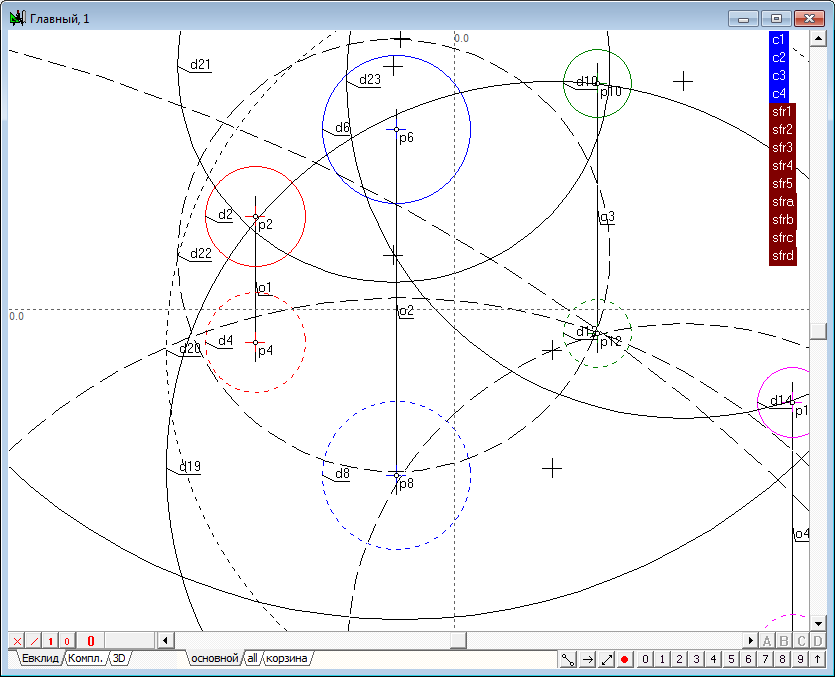
| 28 | Наличие такого алгоритма позволяет, например, выполнить следующее интересное построение: зададим четыре сферы и построим пятую сферу, ортогональную к четырем заданным. Имея теперь пять сфер, построим еще четыре сферы, используя в качестве исходных; 5,1,2,3
|