Пересечение двух плоскостей
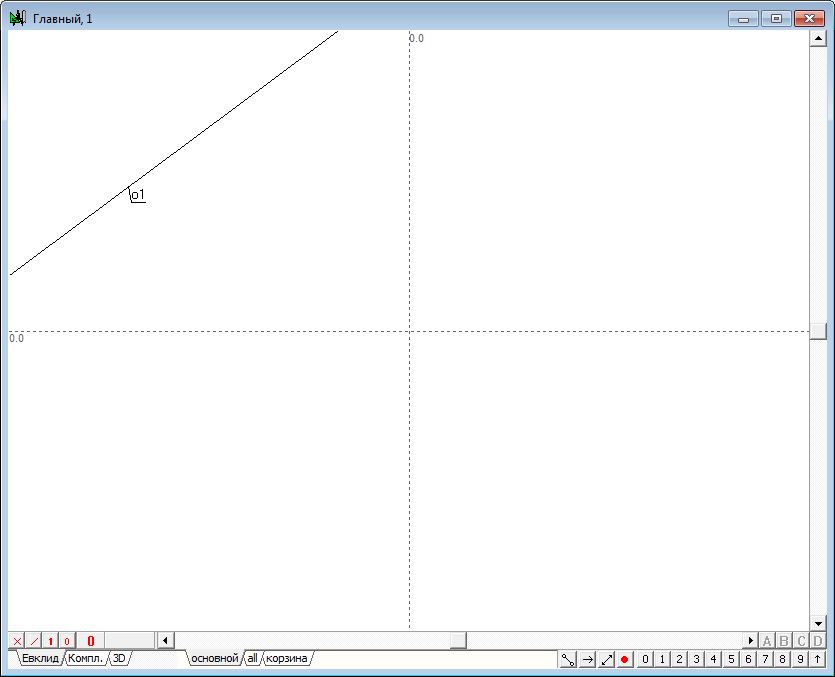
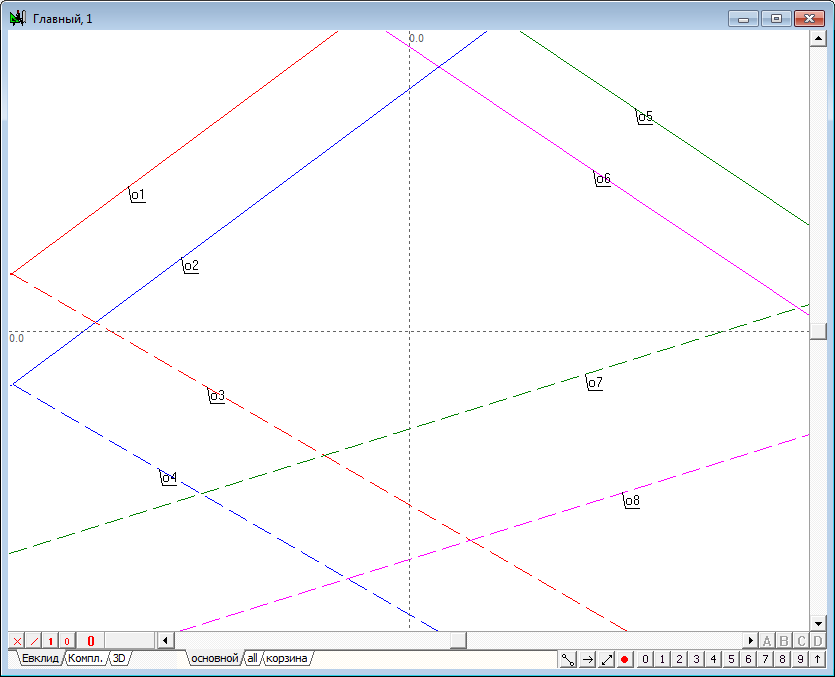
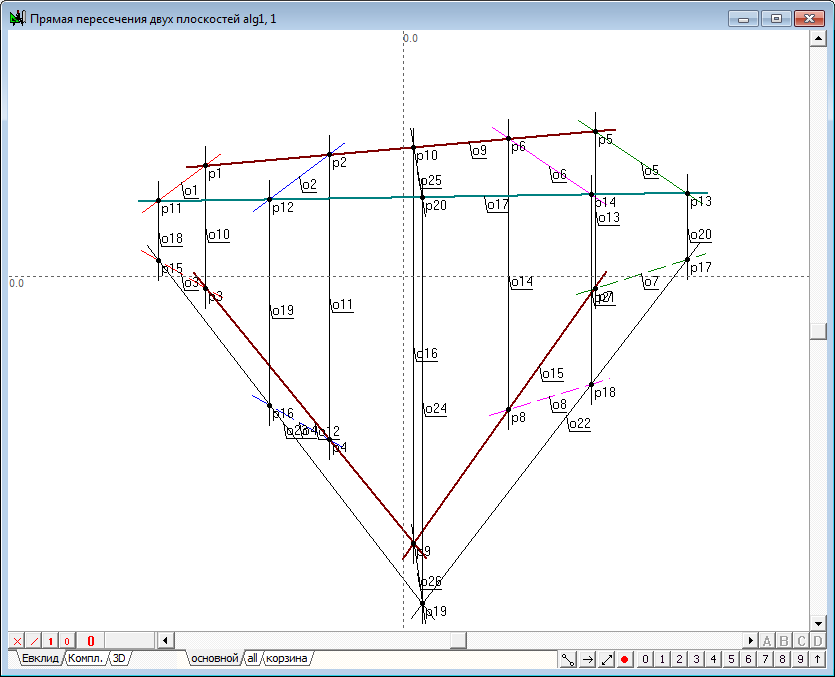
1

Решим задачу пересечения двух плоскостей и оформим ее как самостоятельный алгоритм, которым можно будет пользоваться как процедурой.

Загрузим систему Симплекс и создадим новый проект (Ctrl+N). На экране появится окно для реализации алгоритма с названием Главный. Оставим это окно пустым и создадим новый алгоритм, в котором и реализуем поставленную задачу. Введем с клавиатуры команду Ctrl+Alt+N для открытия окна формирования нового алгоритма с автоматически генерируемым названием alg1.

Зададим первую плоскость парой параллельных линий. Для этого воспользуемся инструментом Свободная прямая и прочертим в окне первую проекцию первой прямой плоскости - o1.
   

Рис. 1
   
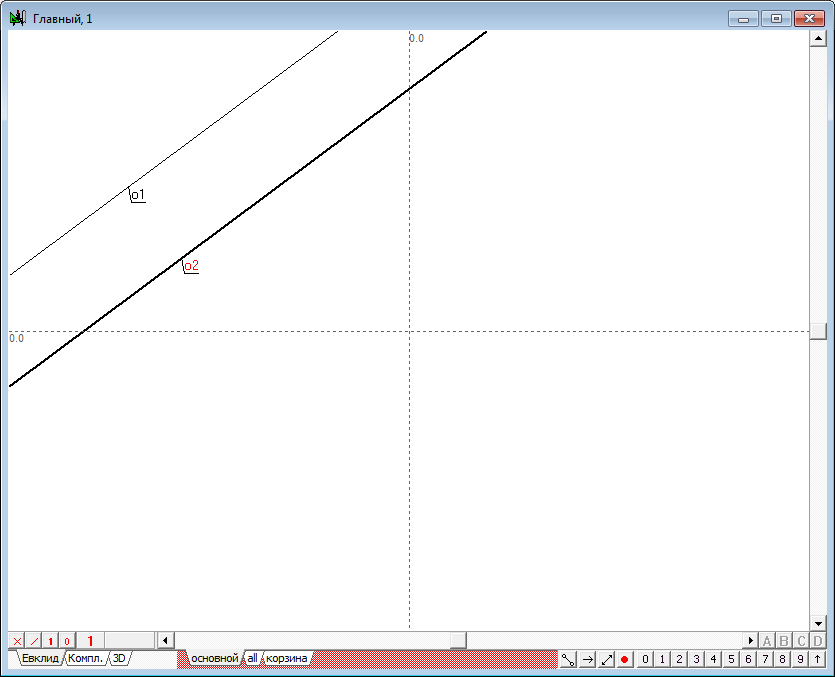
2 Для построения первой проекции второй прямой плоскости, выделим первую прямую, затем переместим курсор на некоторое расстояние от выделенной прямой и нажмем на клавиатуре клавишу с латинским символом o. Данное действие приведет к образованию прямой o2, параллельной прямой o1.
   
 

Рис. 2
   
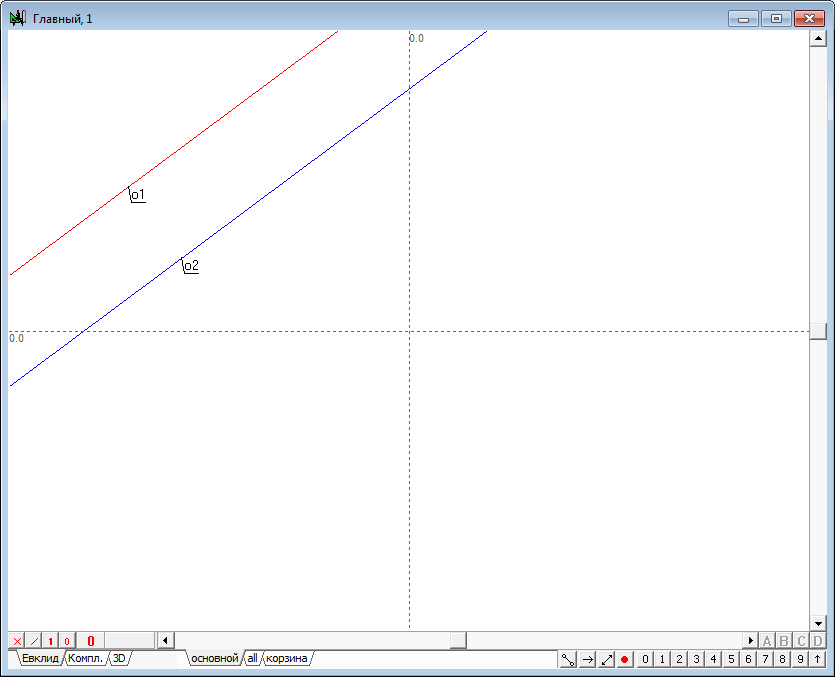
3 Для того чтобы прямые было бы удобно отличать друг от друга изменим цвет их отображения. Пусть прямая o1 будет отмечена красным цветом, а прямая o2 - синим цветом.
   
 

Рис. 3
   
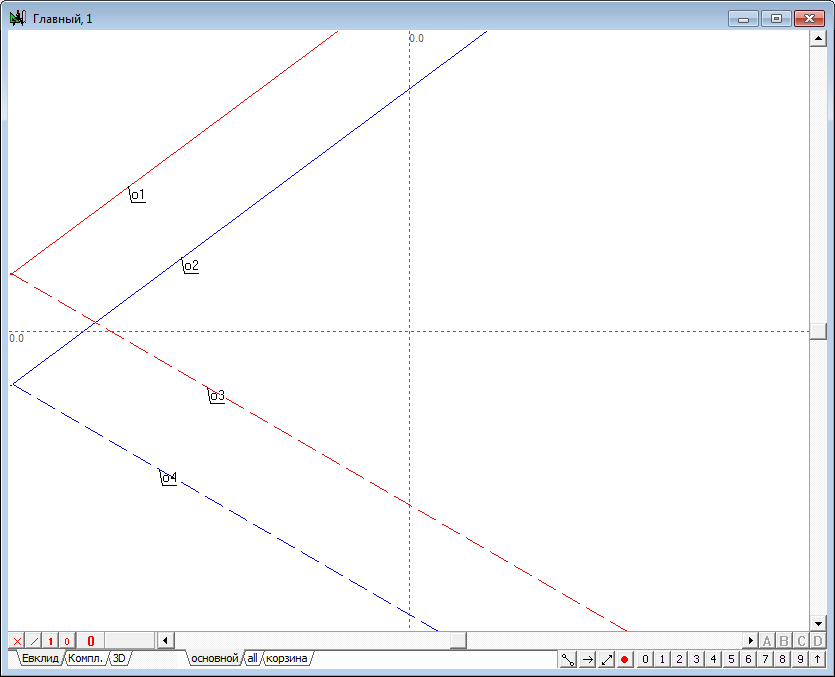
4 Аналогично построим и вторые проекции прямых, также отметив их соответственными цветами. Помимо этого, для того чтобы отличать первые проекции прямых, задающих плоскость, от вторых проекций, изменим начертание последних на штриховое.
   
 

Рис. 4
   
5 Теперь зададим вторую плоскость. Будем действовать по только что рассмотренной схеме, но назначим прямым этой плоскости другие цвета, чтобы отличать первую плоскость от второй.
   
 

Рис. 5
   
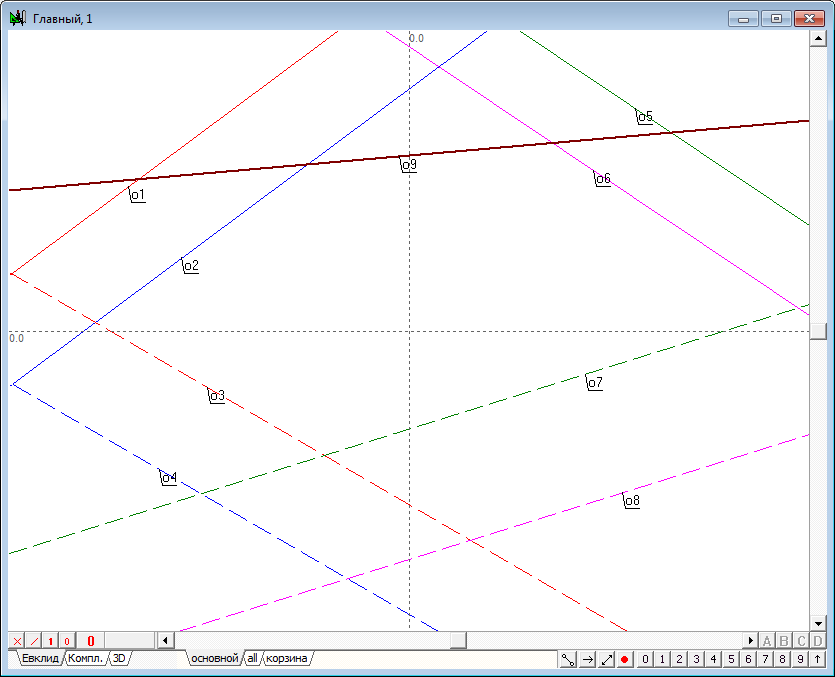
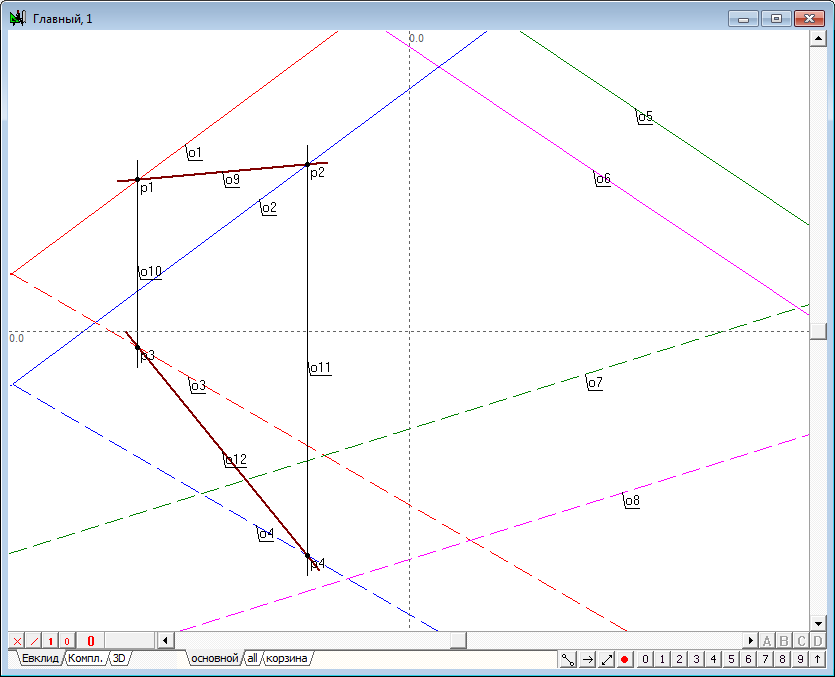
6 Приступим к решению задачи. Проведем плоскость, перпендикулярную фронтальной плоскости проекций. Такая плоскость занимает проецирующее положение, поэтому она будет изображена в первой проекции прямой линией. Пусть она будет задана прямой o9 .
   
 

Рис. 6
   
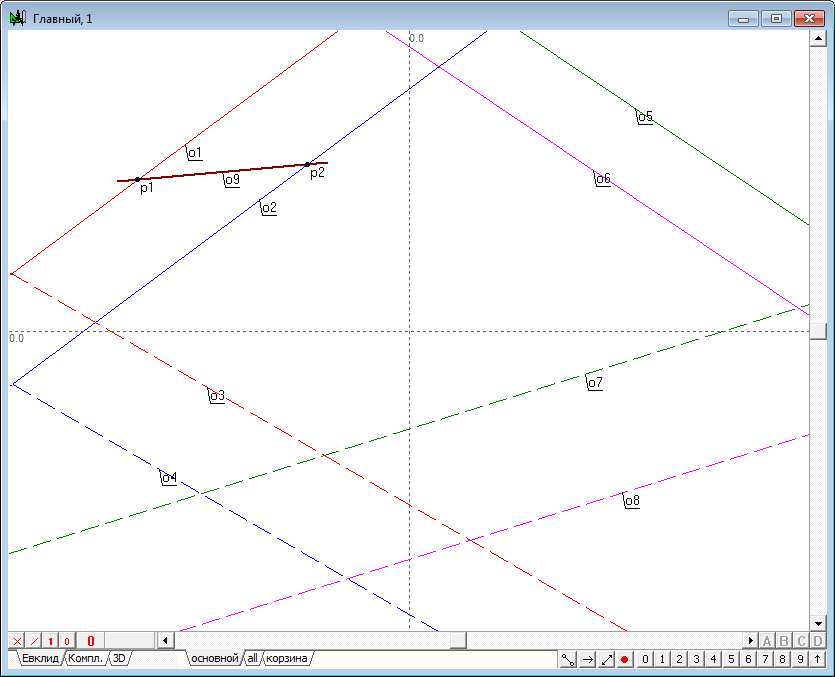
7 Проецирующая плоскость пересекает первую исходную плоскость по прямой линии (поскольку в расширенном трехмерном пространстве любые две несовпадающие плоскости пересекаются по прямой линии). Понятно, что линия пересечения принадлежит проецирующей плоскости, но сама плоскость на проекции изображена прямой линией o9 , следовательно, линия пересечения совпадает с линией, задающей плоскость, поскольку она является одной из всех прямых линий, принадлежащей этой плоскости. Нетрудно найти первые проекции точек, общих для линии пересечения и прямых, задающих первую плоскость. Точки p1 и p2 , обозначающие эти проекции, находятся в результате пересечения прямой o9 с прямыми o1 и o2 . Для их построения выделим соответственные прямые и нажмем на клавиатуре клавишу с латинским символом p.
   
 

Рис. 7
   
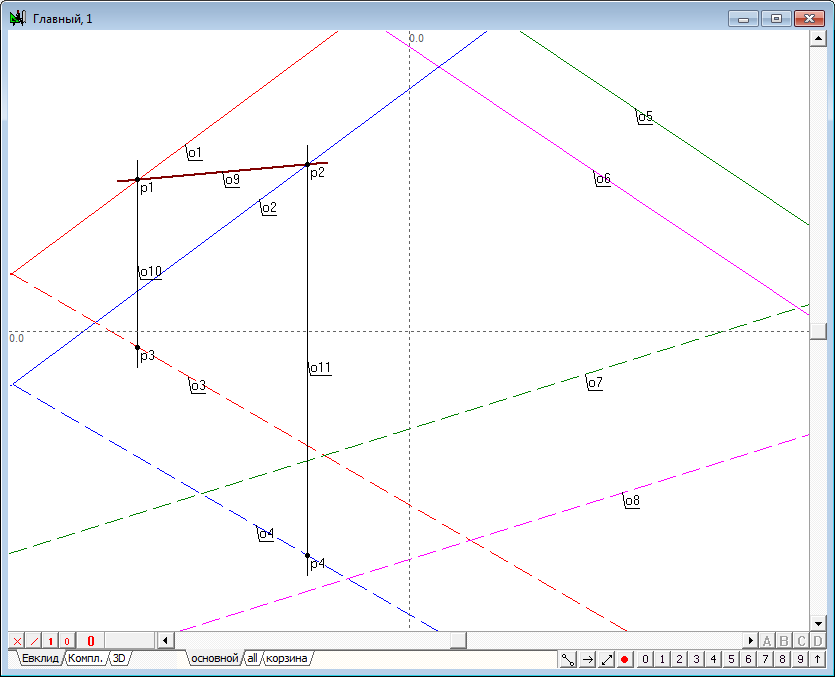
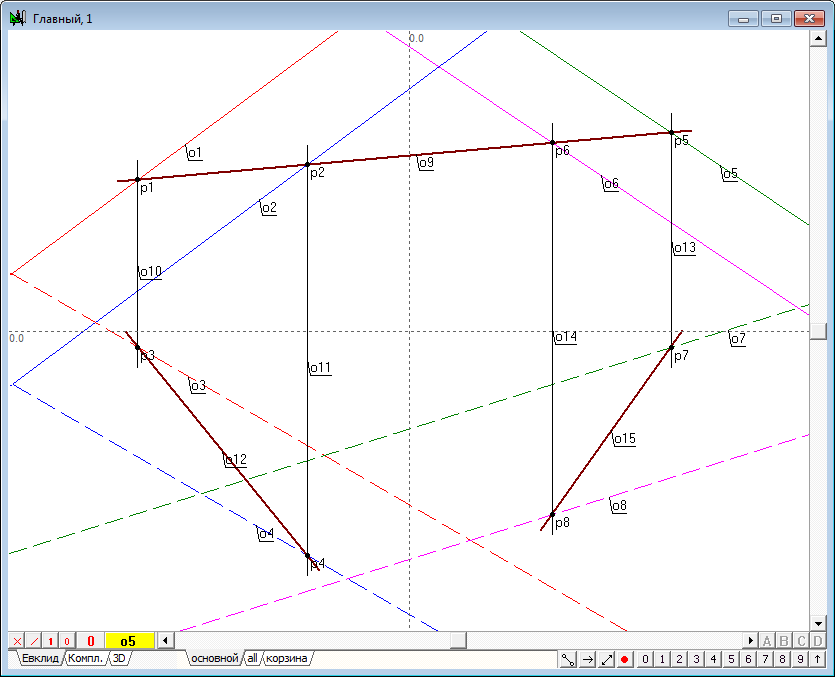
8 Зная первые проекции точек, расположенных на прямых, задающих первую плоскость, нетрудно отыскать их вторые проекции, поскольку эти проекции должны находиться на вторых проекциях соответственных прямых и на линиях связи, проходящих через известные первые проекции. Поэтому, выделив точки и нажмем на клавиатуре клавишу с латинским символом v для построения вертикальных линий связи, а затем найдем пересечение полученных прямых o10 , o11 с соответственными прямыми o3 и o4 . Разумеется, следует обратить внимание на то, чтобы проекции точек располагались на соответственных проекциях прямых, что несложно сделать, обращая внимание на цвет объектов чертежа.
   
 

Рис. 8
   
9 Теперь нам известны две пространственные точки, через которые проходит линия пересечения вспомогательной проецирующей плоскости и первой исходной плоскости. Это значит, что мы можем построить линию пересечения, проведя ее через эти точки. Первая проекция этой прямой уже известна, а вторая, естественно, пройдет через точки p3 и p4 .
   
 

Рис. 9
   
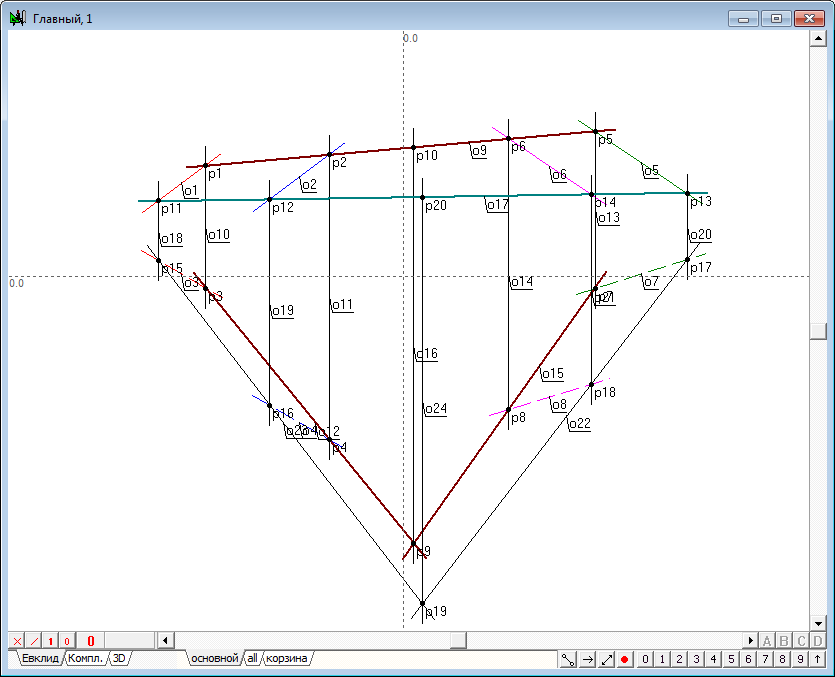
10 Понятно, что та же самая проецирующая плоскость пересекает и вторую исходную плоскость. Причем первая проекция линии пересечения этих плоскостей известна, поскольку она совпадает с прямой линией, задающей проецирующую плоскость. Действуя в точном соответствии со схемой, рассмотренной в отношении первой исходной плоскости, найдем вторую проекцию o15 линии пересечения проецирующей плоскости со второй исходной плоскостью.
   
 

Рис. 10
   
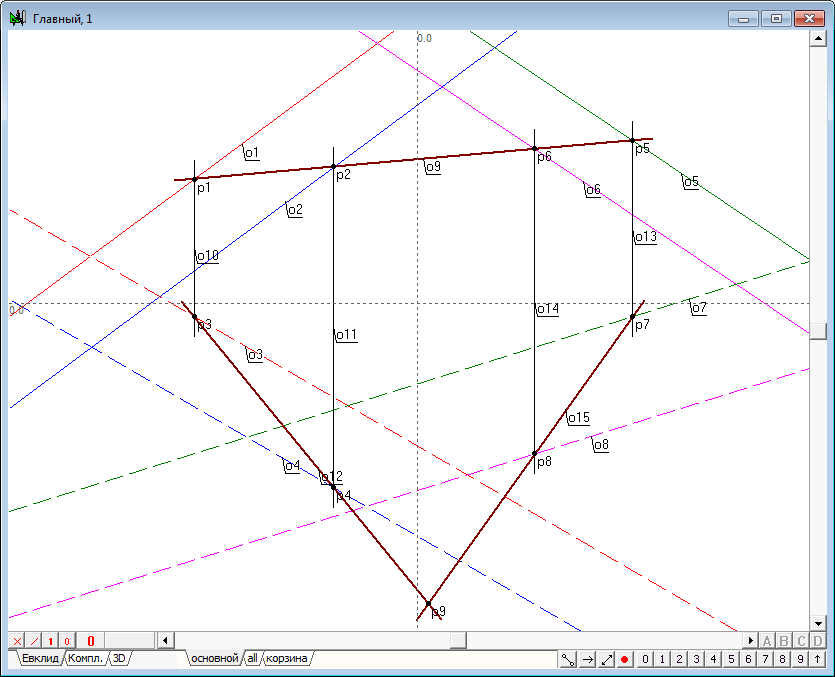
11 Наличие прямых o12 и o15 обеспечивает нам возможность нахождения второй проекции точки, общей сразу для всех трех плоскостей: двух исходных и третьей - проецирующей (три плоскости в пространстве пересекаются в точке). Для ее нахождения пересечем прямые линии o12 и o15 , выделив их и нажав на клавиатуре клавишу с латинским символом p (точка p9).
   
 

Рис. 11
   
12 Не составит труда нахождение и первой проекции этой точки, поскольку она должна располагаться на линии связи и принадлежать проецирующей плоскости. Так как плоскость задана прямой линией o9, то, проведя вертикальную линию o16 через точку p9, найдем ее пересечение с прямой o9. Полученная точка p10 является первой проекцией искомой точки пересечения трех плоскостей.
   
 

Рис. 12
   
13 Итак, мы имеем точку, общую для трех плоскостей. Понятно, что она является обшей для первой и второй исходной плоскости. Поскольку эти плоскости пересекаются по общей прямой и эта прямая, естественно, должна проходить через общие для этих плоскостей точки, то нам остается найти еще одну точку, построенную подобно первой. Что и следует сейчас сделать. Алгоритм построения второй общей точки, естественно, будет точно таким же, как и в случае нахождения первой точки. Нужно лишь задать еще одну проецирующую плоскость, не совпадающую с первой проецирующей плоскостью. Выполним эти построения уже без подробной детализации осуществляемых действий. Проведем произвольную, но не совпадающую с линией o9 прямую o17, моделирующую вторую проецирующую плоскость, и найдем точку, общую для двух исходных плоскостей и второй проецирующей плоскости. Эта точка определяется своими проекциями - точками p20 и p19 .
   
 

Рис. 13
   
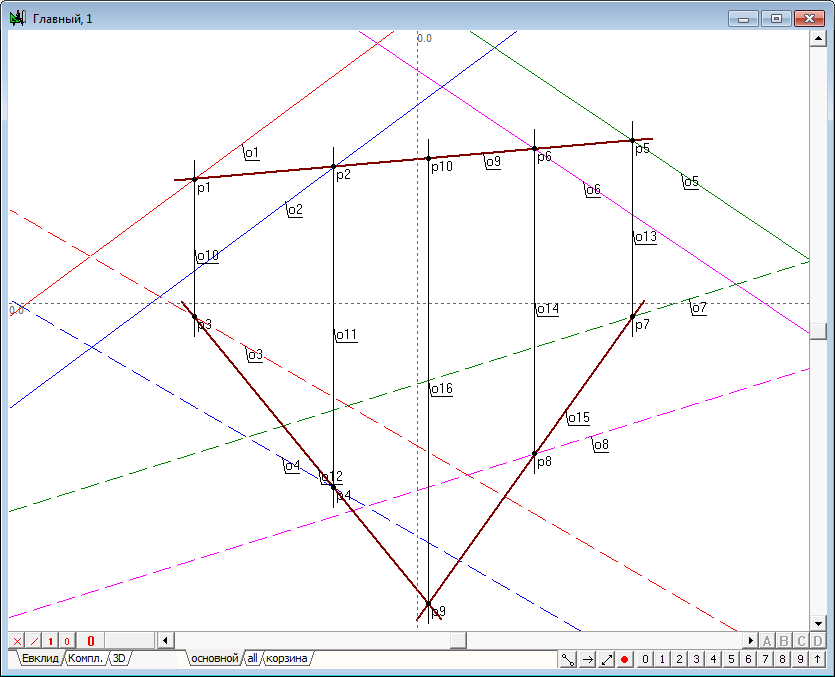
14 Нам остается провести прямую линию через две найденные точки, являющимися общими для двух исходных плоскостей, следовательно, прямая линия (o25 , o26), являющаяся результатом пересечения этих плоскостей, найдена.
   
 

Рис. 14
   
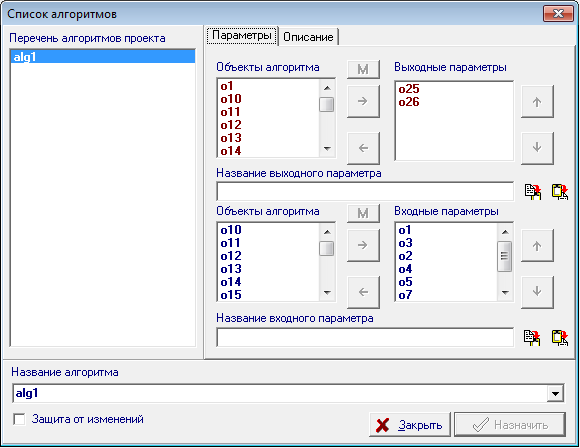
15

Оформим теперь алгоритм как процедуру. Укажем и опишем те объекты, которые являются его входными и выходными параметрами, а также дадим название этому алгоритму.

Первое, что необходимо сделать, это выделить в определенной последовательности те объекты, которые мы хотим сделать входными параметрами процедуры. На этом этапе следует определиться с тем, в какой последовательности мы будем задавать эти параметры, поскольку в дальнейшем при использовании процедуры в качестве самостоятельной команды, эту последовательность будет необходимо соблюдать при передаче фактических параметров в эту процедуру.

Пусть параметры заданы в следующей последовательности:
- первая проекция первой прямой первой плоскости;
- вторая проекция первой прямой первой плоскости;
- первая проекция второй прямой первой плоскости;
- вторая проекция второй прямой первой плоскости;
- первая проекция первой прямой второй плоскости;
- вторая проекция первой прямой второй плоскости;
- первая проекция второй прямой второй плоскости;
- вторая проекция второй прямой второй плоскости.

Удерживая нажатой клавишу Shift, выделим необходимые для указания параметров объекты в следующей последовательности: o1 , o3 , o2 , o4 , o5 , o7 , o6 , o8 и, вызвав правой кнопкой мыши контекстное меню, выберем в нем пункт Назначить o1 , o3 , o2 , o4 , o5 , o7 , o6 , o8 входом алгоритма. Сразу после ввода команды система начнет выводить запросы об именовании параметров, соответствующих указанным объектам (их названия соответствуют только что рассмотренному перечню параметров). При желании названия можно ввести во время этого диалога, но аналогичное действие можно выполнить и позже, осуществляя общую настройку процедурных характеристик алгоритма. В этом случае следует согласиться со всеми предлагаемыми системой названиями, соответствующими именам только что выделенных и назначенных в качестве параметров объектов.

Второе действие связано с выделением объектов, которые следует рассматривать в качестве выходных параметров алгоритма. В нашем случае - это проекции прямой пересечения плоскостей. Выделим объекты o25 , o26 и, вызвав правой кнопкой мыши контекстное меню, выберем в нем пункт Назначить o25 , o26 выходом алгоритма.

Теперь, воспользовавшись контекстным всплывающим меню окна, в котором разрабатывался алгоритм, вызовем диалоговое окно для его настройки, выбрав пункт Алгоритм этого меню. На экране появится следующее диалоговое окно:
   
 

Рис. 15
   
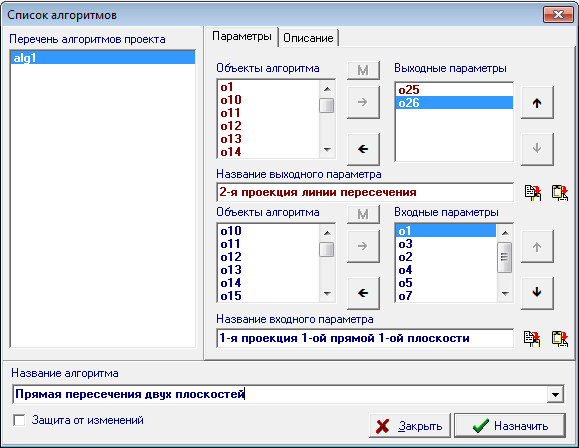
16 Последовательно выделяя объекты в списках Выходные параметры и Входные параметры укажем названия этих параметров. Поскольку в названиях параметров прослеживается некоторая общность, то имеет смысл воспользоваться кнопками для занесения текста из панелей Название выходного параметра и Название входного параметра в буфер Clipboard посредством нажатия на кнопку , расположенную возле соответственного поля ввода. При переходе к формированию названия следующего параметра посредством нажатия на кнопку в поле ввода названия можно ввести ранее сохраненный в буфере Clipboard текст, после чего сделать в нем необходимые изменения, что несколько упрощает работу и способствует снижению количества ошибок. В этом же окне следует также указать и название самого алгоритма.
   
 

Рис. 16
   
17 После выполненных назначений окно реализации алгоритма примет следующий вид:
   
 

Рис. 17
   
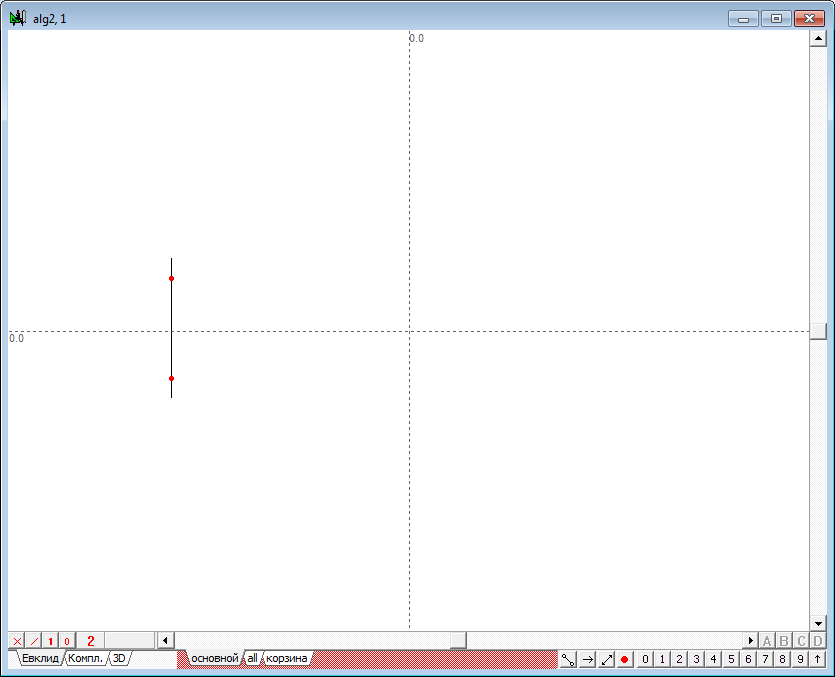
18

Для проверки работоспособности алгоритма создадим новый алгоритм и зададим в нем две произвольные плоскости. Для этого следует нажать клавиши Ctrl+Alt+N, что приведет к открытию окна для формирования нового алгоритма alg2.

Зададим плоскости следующим образом: разместим курсор над свободным пространством окна и нажмем клавишу с латинской букой V (верхний регистр). Это действие приведет к формированию модели трехмерной точки - конструкции из двух точек и несущих их прямой, представленной на рисунке.
   
 

Рис. 18
   
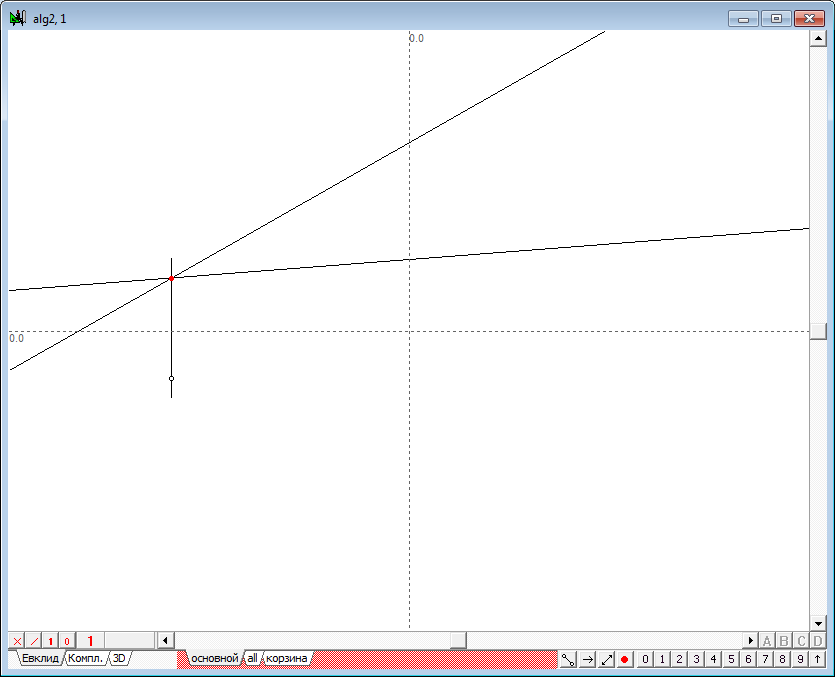
19 Щелкнув левой кнопкой мыши над свободным от изображений объектов пространстве окна, снимем выделение с точек, а затем выделим верхнюю точку еще раз. Отведя курсор от точки на некоторое расстояние, нажмем на клавиатуре клавишу с латинским символом o, что приведет к построению прямой линии, проходящей через выделенную точку под некоторым углом к оси OX, определяемым текущим положением курсора на экране. Сместим курсор еще немного и повторим предыдущую команду. В результате будет построена еще одна прямая. Этими действиями мы задали первые проекции двух пересекающихся прямых, определяющих первую исходную плоскость в проверочном алгоритме.
   
 

Рис. 19
   
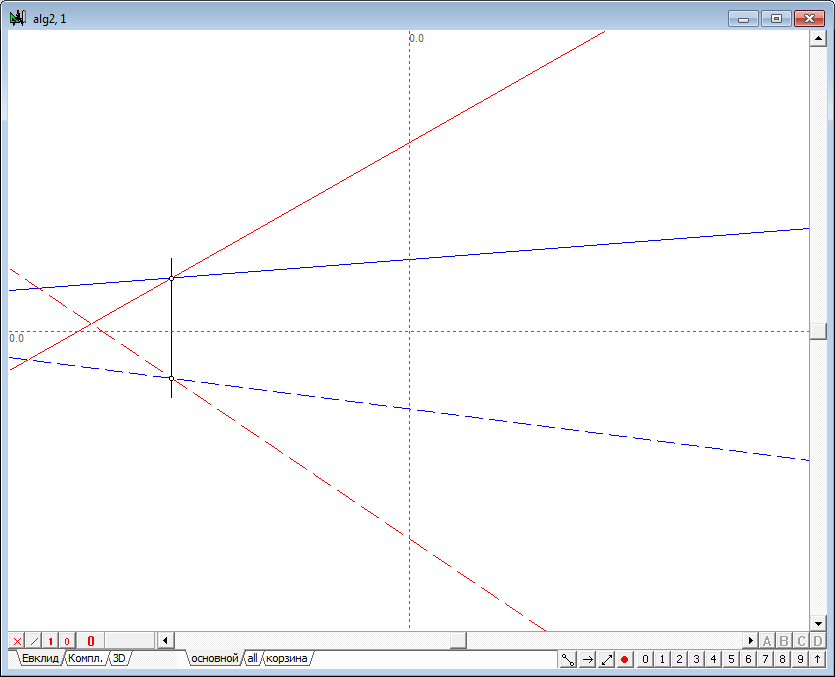
20 Изменим цвет прямых, а затем выполним аналогичные действия для задания вторых проекций прямых, определяющих первую исходную плоскость.
   
 

Рис. 20
   
21 Подобным образом зададим и вторую плоскость.
   
 

Рис. 21
   
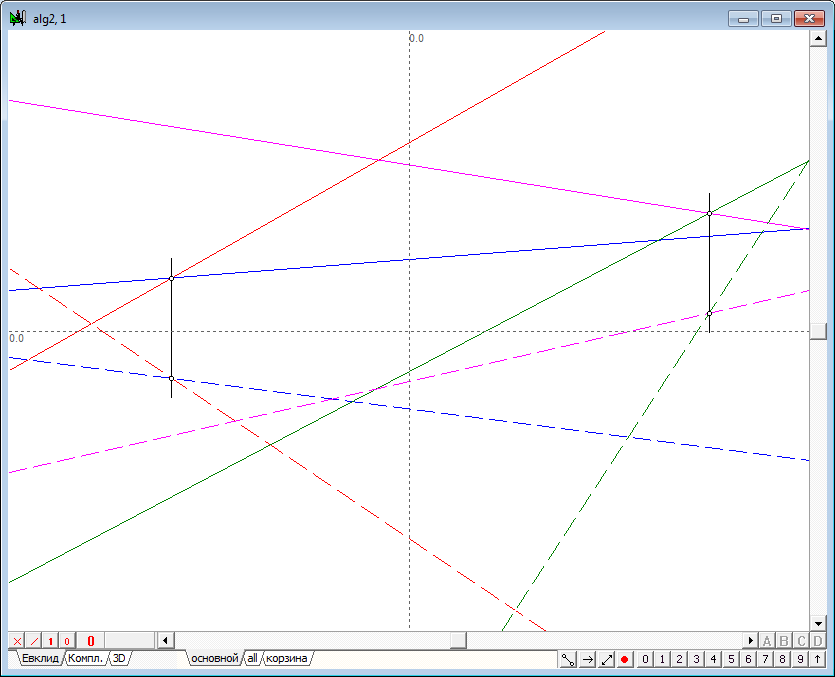
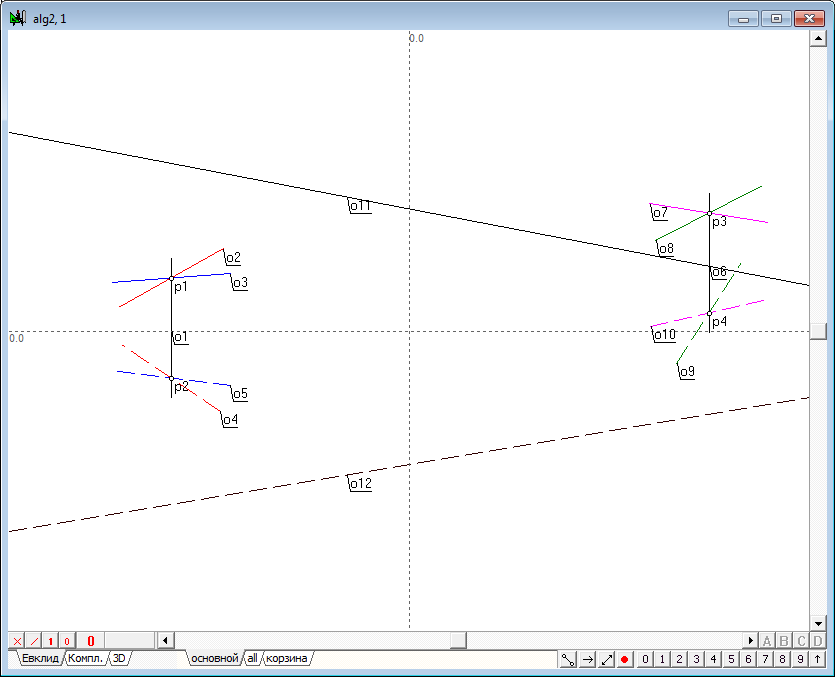
22 Из рисунка видно, что построенные прямые достаточно интенсивно заполняют рабочую область чертежа. При большом количестве линий это обстоятельство может доставлять определенные неудобства. Имеет смысл ограничить длину отображаемых линий, подразумевая однако, что эти линии являются бесконечными прямыми. Выделим линии, задающие обе плоскости, и нажмем на клавишу с цифрой 9. Полученное изображение приведено на рисунке.
   
 

Рис. 22
   
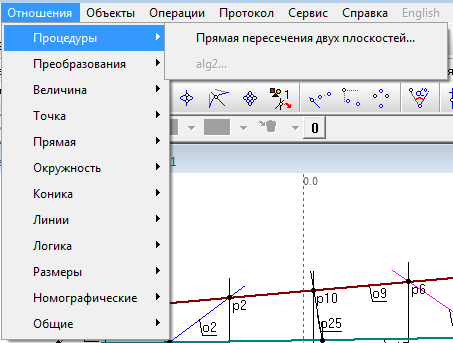
23 И, наконец, воспользуемся подготовленной ранее процедурой для нахождения линии пересечения двух заданных плоскостей. Процедура вызывается из пункта меню Отношения/Процедуры/Прямая... пересечения двух плоскостей (активным окном, из которого осуществляется вызов процедуры, должно быть, разумеется, окно алгоритма alg2).
   
 

Рис. 23
   
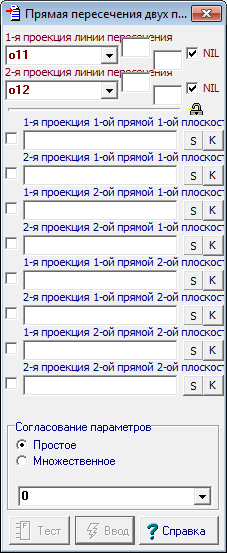
24 Вызов пункта меню приведет к появлению диалогового окна для формирования команды
   
 

Рис. 24
   
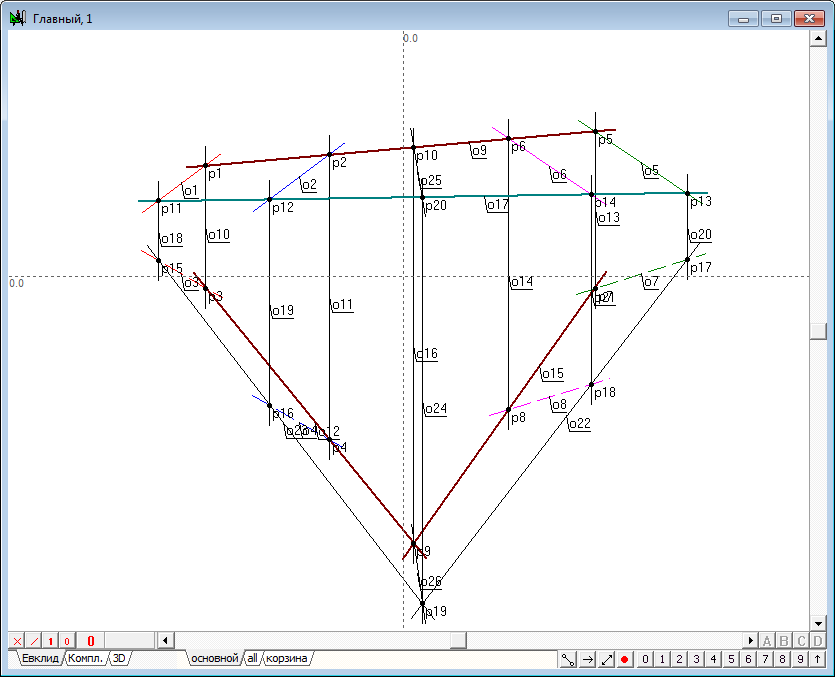
25 Заполним поля этого диалога именами объектов в строгом соответствии с порядком, установленным для параметров вызываемой процедуры:
   
 

Рис. 25
   
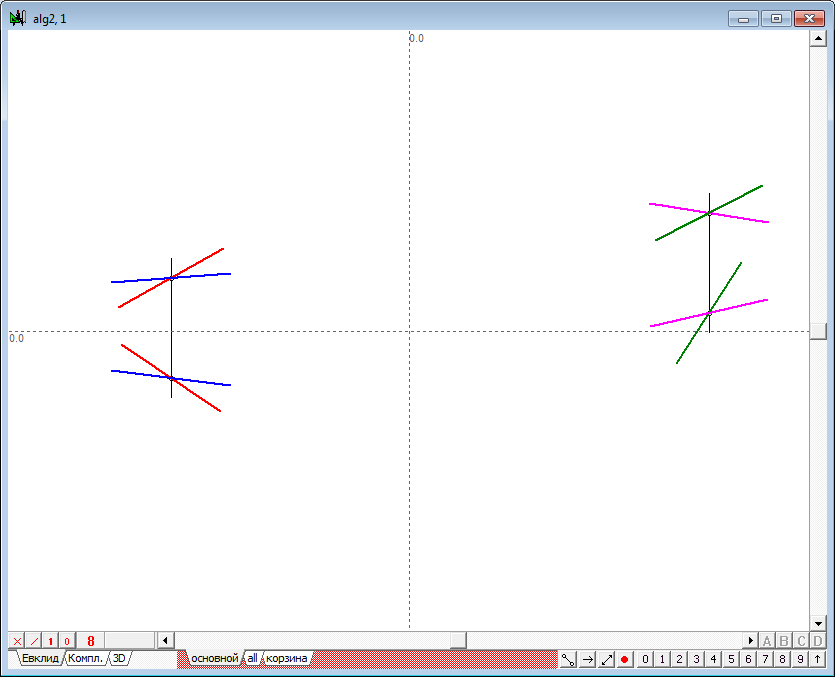
26 После нажатия на кнопку Ввод будет получено решение. Пространственная прямая, моделируемая проекциями o11 и o12 есть результат пересечения двух плоскостей, заданных пересекающимися прямыми (o2 , o4 ) - ( o3 , o5 ) и (o7 , o10 ) - (o8 , o9 ). Изменяя при помощи шейпера положение проекций прямых, будем получать различные решения поставленной задачи.
   
 

Рис. 26
   
  Пример