Центроид треугольника

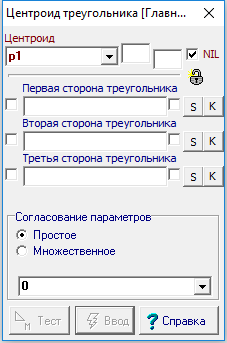
Отношение предназначено для построения центроида треугольника. Центроид треугольника — это точка пересечения его медиан. Подробнее см. центроид треугольника.

Если тип объекта, указанного во входном параметре, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.

Параметры	Типы объектов	Функциональное назначение параметров
Центроид	Точка	Центроид треугольника
Первая сторона треугольника	Прямая	Первая сторона треугольника
Вторая сторона треугольника	Прямая	Вторая сторона треугольника
Третья сторона треугольника	Прямая	Третья сторона треугольника

Прототип команды: TR009 Согласование Центроид ; Первая_сторона_треугольника Вторая_сторона_треугольника Третья_сторона_треугольника .

Входные параметры: o1, o2, o3.

Выходной параметр:p7.

Алгоритм "Главный"

1		Прямая o1 задана координатами двух точек: X1= -340.5 , Y1= -38 , X2= -239.5 , Y2= 51 .
2		Прямая o2 задана координатами двух точек: X1= -268.5 , Y1= 182 , X2= -53.5 , Y2= 23 .
3		Прямая o3 задана координатами двух точек: X1= 257.5 , Y1= -109 , X2= -68.5 , Y2= -99 .
4		Точка p1 есть пересечение прямых o1 и o2 .
5		Точка p2 есть пересечение прямых o2 и o3 .
6		Точка p3 есть пересечение прямых o3 и o1 .
7		Прямая o4 задана точками p1 и p2 .
8		Прямая o5 задана точками p2 и p3 .
9		Прямая o6 задана точками p3 и p1 .
10		Точка p4 есть центр объекта o4 .
11		Точка p5 есть центр объекта o5 .
12		Точка p6 есть центр объекта o6 .
13		Прямая o7 задана точками p3 и p4 .
14		Прямая o8 задана точками p1 и p5 .
15		Точка p7 есть пересечение прямых o7 и o8 .

Структура функции

Пример 1:

Построить центроид p4 треугольника, заданного на вершинах p1, p2 и p3.

Алгоритм "Главный"

1		Точка p1 задана координатами -148.5 и -87 .
2		Точка p2 задана координатами -17.5 и 107 .
3		Точка p3 задана координатами 90.5 и -58 .
4		Прямая o1 задана точками p1 и p2 .
5		Прямая o3 задана точками p2 и p3 .
6		Прямая o5 задана точками p3 и p1 .
7		Центроид p4 треугольника, построенного на прямых o1 , o3 , o5 .