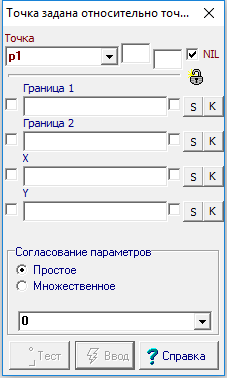
Точка задана координатами с двойной линейной границей |
|
| |
Отношение предназначено для задания собственной точки вещественной плоскости Точка посредством указания ее координат X и Y и двух прямых линий Граница 1 и Граница 2, ограничивающих свободу перемещения точки. Точка может располагаться только в области взаимного пересечения полуплоскостей, определенных положительными направлением первой и второй граничных прямых. Если в отношении будут заданы координаты, располагающие точку в области, противоположной прересечению "разрешенных" областей, заданных положительными направлениями граничных прямых, то в этом для построения точки будут использованы следующие правила:
1. если указываемая позиция точки находится в "разрешенной" области по отношению к одной граничной прямой, но в "запрещенной" по отношению к другой граничной прямой, то в этом случае окончательным положением задаваемой точки будет ортогональная проекция точки, заданной введенными координатами, на прямую, определившую "запрещенную" полуплоскость;
2.
если указываемая позиция точки находится сразу в обеих запрещенных областях, определенных граничными прямыми, то ее окончательное положение будет совпадать с точкой пересечения обеих граничных прямых.
Рассмотренный способ задания точки позволяет ограничивать возможные перемещения точки при динамическом редактировании ее положения посредством указания двух граничных прямых.
Если тип объекта, указанного в любом из входных параметров, оказывается несовместимым с типом этого параметра, то при установленном флажке NIL в выходной параметр заносится значение NIL-объекта.
Функция позволяет ограничить перемещение свободной точки во время динамического редактирования шейпером в пределах сектора плоскости, заданного граничными прямыми.
|
|
| |
|
Параметры |
Типы объектов |
Функциональное назначение
параметров |
|
Точка |
Точка |
Определяемая точка |
|
Граница 1 |
Прямая |
Первая прямая линия, ограничивающая свободу размещения (перемещения) точки |
|
Граница 2 |
Прямая |
Вторая прямая линия, ограничивающая свободу размещения (перемещения) точки |
|
X |
Величина, точка |
Значение X-координаты |
|
Y |
Величина, точка |
Значение Y-координаты |
|
| |
Прототип команды: P0A Согласование Точка; Граница_1 Граница_2 X Y .
|
| |
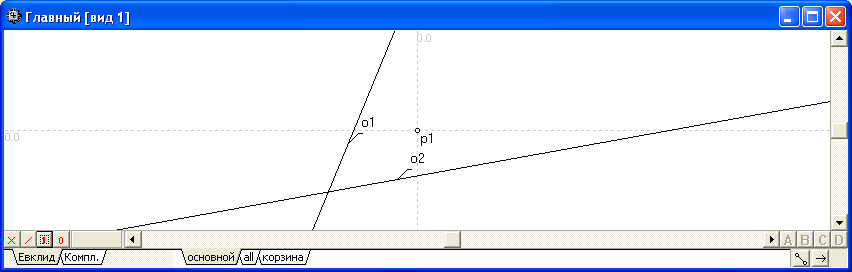
Пример 1:
Задать точку с координатами X=0, Y=0 при условии ее свободного размещения справа по отношению к ориентации прямых линий o1 и o2.
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -110.5 , Y1= -112.5 , X2= -27.5 , Y2= 87.5 . |
2 |
|
Точка p1 задана координатами 0 и 0 с прямыми-границами o1 и -o2 . |
3 |
|
Прямая o2 задана координатами двух точек: X1= -186.5 , Y1= -78.5 , X2= 146.5 , Y2= -18.5 . |
|

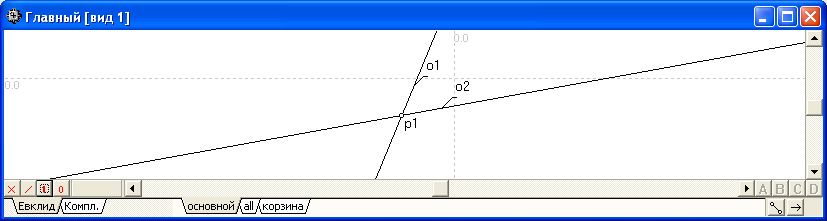
Пример 2:
Задать точку с координатами X=-100, Y=80 при условии ее свободного размещения справа по отношению к ориентации прямой линии o1.
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -110.5 , Y1= -112.5 , X2= -27.5 , Y2= 87.5 . |
2 |
|
Прямая o2 задана координатами двух точек: X1= -186.5 , Y1= -78.5 , X2= 146.5 , Y2= -18.5 . |
3 |
|
Точка p1 задана координатами -100 и -80 с прямыми-границами o1 и -o2 . |
|

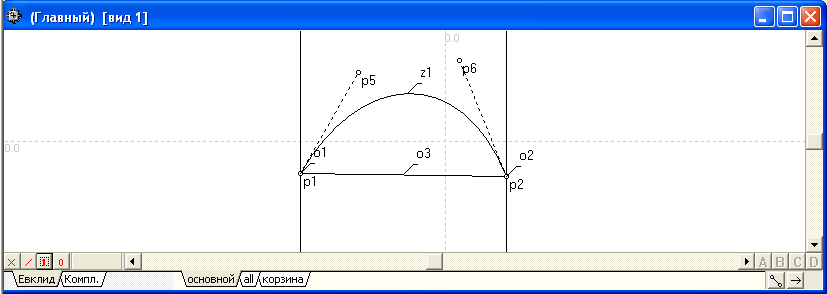
Пример 3:
Задать кривую Безье z1 таким образом, чтобы динамическое редактирование положения управляющих точек p5 и p6 исключало бы возможность пересечения кривой z1 с граничными прямыми o1, o2 и o3.
Алгоритм "Главный" |
1 |
|
Точка p1 задана координатами -144.5 и -31.5 . |
2 |
|
Точка p2 задана координатами 61.5 и -34.5 . |
3 |
|
Прямая o1 задана точкой p1 и углом rect к оси OX. |
4 |
|
Прямая o2 задана точкой p2 и углом rect к оси OX. |
5 |
|
Прямая o3 задана точками p1 и p2 . |
6 |
|
Точка p5 задана координатами -87 и 69.5 с прямыми-границами o1 и -o3 . |
7 |
|
Точка p6 задана координатами 14 и 81.5 с прямыми-границами -o2 и -o3 . |
8 |
|
Кривая Безье z1 - на точках p1 , p5 , p6 , p2 . |
|

|
| |
|
| |
|
| |
|
| |
|