Эллипс Мандара

Отношение предназначено для построения эллипса Мандара, индуцированного треугольником.

Если тип объекта, указанного во входном параметре, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.

Параметры	Типы объектов	Функциональное назначение параметров
Эллипс	Коника	Эллипс Мандара
Точка 1	Точка	Точка касания эллипса с первой стороной треугольника
Точка 2	Точка	Точка касания эллипса со второй стороной треугольника
Точка 3	Точка	Точка касания эллипса с третьей стороной треугольника
Первая сторона треугольника	Прямая	Первая сторона исходного треугольника
Вторая сторона треугольника	Прямая	Вторая сторона исходного треугольника
Третья сторона треугольника	Прямая	Третья сторона исходного треугольника

Прототип команды: TR023 Согласование Эллипс Точка_1 Точка_2 Точка_3 ; Первая_сторона_треугольника Вторая_сторона_треугольника Третья_сторона_треугольника .

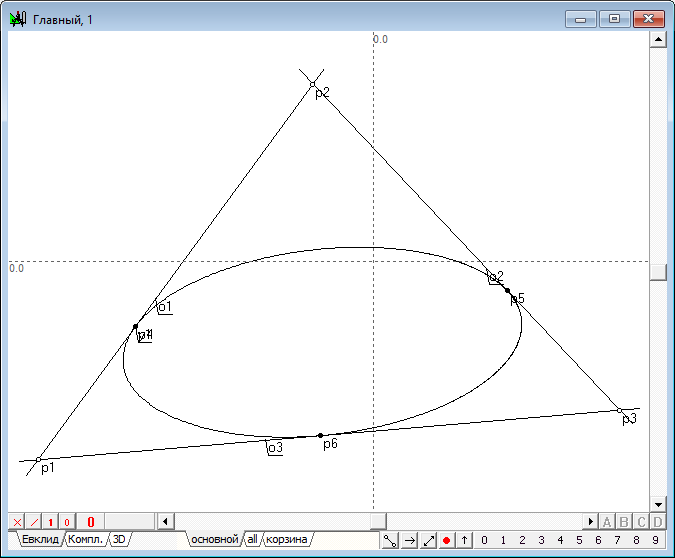
Пример: Построить эллипс Мандара, индуцированный заданным треугольником.

1		Точка p3 задана координатами 130 и -78.5 .
2		Точка p2 задана координатами -32 и 93.5 .
3		Прямая o2 задана точками p2 и p3 .
4		Точка p1 задана координатами -177 и -104.5 .
5		Прямая o3 задана точками p3 и p1 .
6		Прямая o1 задана точками p1 и p2 .
7		Эллипс Мандара y1 и точки p4 , p5 , p6 для треугольника, построенного на прямых o1 , o2 , o3 .

Структура алгоритма

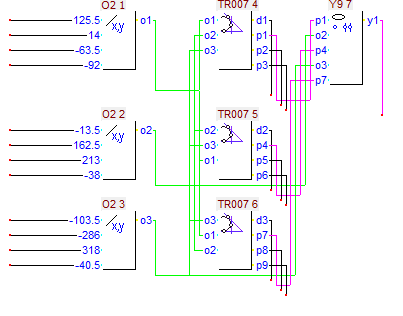
1		Прямая o1 задана координатами двух точек: X1= -92 , Y1= -63.5 , X2= 14 , Y2= 125.5 .
2		Прямая o2 задана координатами двух точек: X1= -38 , Y1= 162.5 , X2= 213 , Y2= -13.5 .
3		Прямая o3 задана координатами двух точек: X1= 318 , Y1= -40.5 , X2= -286 , Y2= -103.5 .
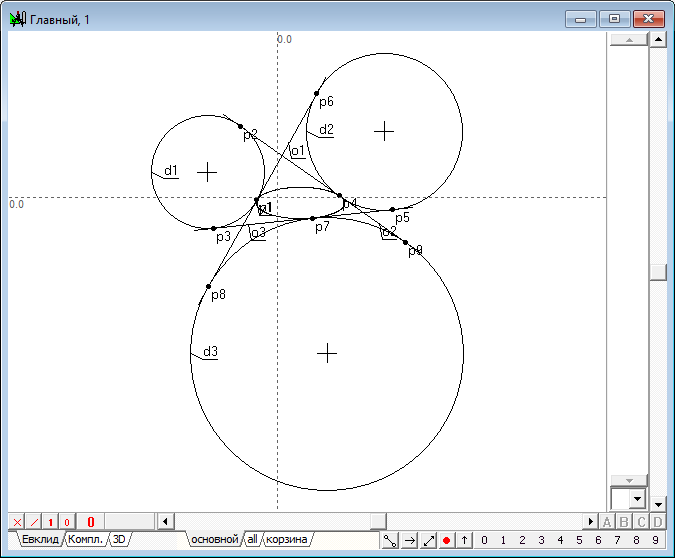
4		Вневписанная окружность d1 , касается треугольника, построенного на прямых o1 , o2 , o3 , в точках p1 , p2 , p3 .
5		Вневписанная окружность d2 , касается треугольника, построенного на прямых o2 , o3 , o1 , в точках p4 , p5 , p6 .
6		Вневписанная окружность d3 , касается треугольника, построенного на прямых o3 , o1 , o2 , в точках p7 , p8 , p9 .
7		Коника y1 по точке p1 , касательной o2 в точке p4 и касательной o3 в точке p7 .