Сфера в инверсии относительно сферы |
|
| |
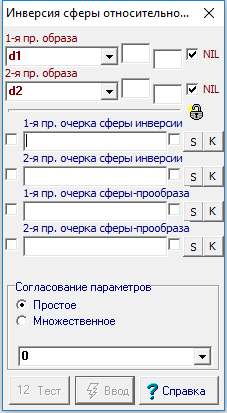
Отношение предназначено для построения модели сферической поверхности относительно сферы в трехмерном пространсве средствами эпюра Монжа.
Если тип объекта, указанного в любом из входных параметров, несовместим с типом этого параметра, то при активизированном флажке NIL в выходной параметр заносится NIL-объект.
|
|
| |
|
Параметры |
Типы объектов |
Функциональное назначение параметров |
|
1-я пр. образа |
Окружность |
Первая проеция (фронтального) очерка сферы-образа |
 |
2-я пр. образа |
Окружность |
Вторая проеция (горизонтального) очерка сферы-образа |
|
1-я пр. очерка сферы инверсии |
Окружность |
Первая проекция очерка сферы инверсии |
|
2-я пр. очерка сферы инверсии |
Окружность |
Вторая проекция очерка сферы инверсии |
|
1-я пр. очерка сферы-прообраза |
Окружность |
Первая проекция очерка сферы-прообраза |
 |
2-я пр. очерка сферы-прообраза |
Окружность |
Вторая проекция очерка сферы-прообраза |
|
| |
Прототип команды: SPSPYI Согласование 1-я_пр._образа 2-я_пр._образа ; 1-я_пр._очерка_сферы_инверсии 2-я_пр._очерка_сферы_инверсии 1-я_пр._очерка_сферы-прообраза 2-я_пр._очерка_сферы-прообраза .
|
| |
Пример:
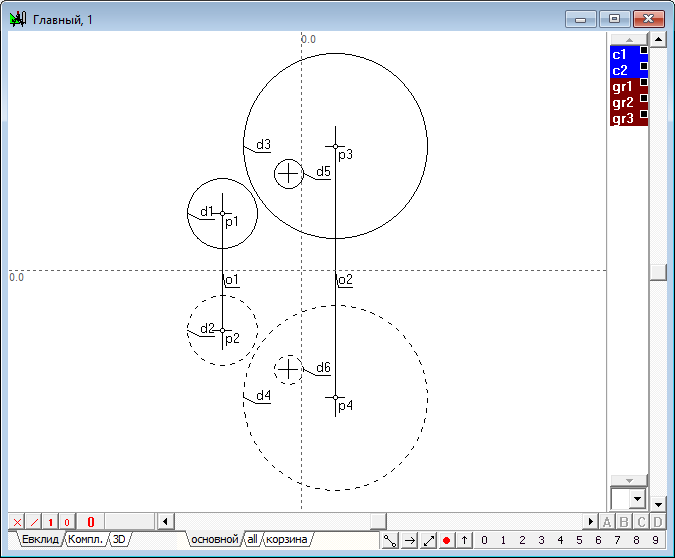
Поcтроить образ заданной сферы в инверсии относительно сферы.
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -96.5 , Y1= 47.5 , X2= -96.5 , Y2= -52.5 . |
2 |
|
Величина c1 есть 42.412371 . |
3 |
|
Точка p1 принадлежит объекту o1 с параметром принадлежности -0.21878828 . |
4 |
|
Окружность d1 задана центром p1 и радиусом c1 . |
5 |
|
Точка p2 принадлежит объекту o1 с параметром принадлежности 1.2026485 . |
6 |
|
Окружность d2 задана центром p2 и радиусом c1 . |
7 |
|
Прямая o2 задана координатами двух точек: X1= 40.5 , Y1= 42.5 , X2= 40.5 , Y2= -57.5 . |
8 |
|
Величина c2 есть 111.83023 . |
9 |
|
Точка p3 принадлежит объекту o2 с параметром принадлежности -1.08 . |
10 |
|
Окружность d3 задана центром p3 и радиусом c2 . |
11 |
|
Точка p4 принадлежит объекту o2 с параметром принадлежности 1.97 . |
12 |
|
Окружность d4 задана центром p4 и радиусом c2 . |
13 |
|
Группа gr1 из компонентов d1,d2 . |
14 |
|
Группа gr2 из компонентов d3,d4 . |
15 |
|
Образ ( d5 - d6 ) сферы ( d1 - d2 ) в инверсии относительно сферы ( d3 - d4 ). |
16 |
|
Группа gr3 из компонентов d5,d6 . |
|
 |
| |
 |
| |
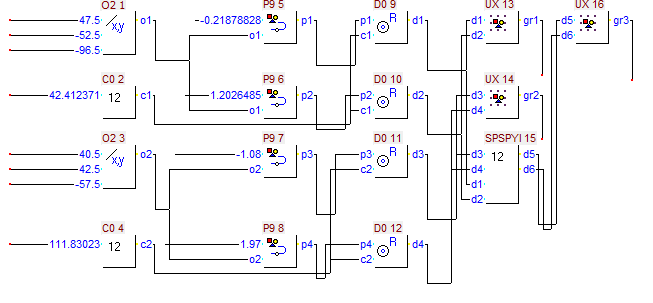
| Структура алгоритма |
| |
Алгоритм "Главный" |
1 |
|
Прямая o1 задана координатами двух точек: X1= -96.5 , Y1= 47.5 , X2= -96.5 , Y2= -52.5 . |
2 |
|
Величина c1 есть 42.412371 . |
3 |
|
Точка p1 принадлежит объекту o1 с параметром принадлежности -0.21878828 . |
4 |
|
Окружность d1 задана центром p1 и радиусом c1 . |
5 |
|
Точка p2 принадлежит объекту o1 с параметром принадлежности 1.2026485 . |
6 |
|
Окружность d2 задана центром p2 и радиусом c1 . |
7 |
|
Прямая o2 задана координатами двух точек: X1= 40.5 , Y1= 42.5 , X2= 40.5 , Y2= -57.5 . |
8 |
|
Величина c2 есть 111.83023 . |
9 |
|
Точка p3 принадлежит объекту o2 с параметром принадлежности -1.08 . |
10 |
|
Окружность d3 задана центром p3 и радиусом c2 . |
11 |
|
Точка p4 принадлежит объекту o2 с параметром принадлежности 1.97 . |
12 |
|
Окружность d4 задана центром p4 и радиусом c2 . |
13 |
|
Группа gr1 из компонентов d1,d2 . |
14 |
|
Группа gr2 из компонентов d3,d4 . |
15 |
|
d5:15@lv=5 d6:16@lt=1@lv=5 d3 d4 d1 d2 |
16 |
|
Группа gr3 из компонентов d5,d6 . |
|
|
| |
 |
| |
 |
| |
|
| |
|
| |
|
| |
|