Плоскость четырьмя точками

Отношение предназначено для задания плоского объекта на основе четырех компланарных точек, расположенных в трехмерном пространстве.

	Клавиша	Предварительно выделено:	Действие	Выделение после действия:

Параметры	Типы объектов	Функциональное назначение параметров
Плоскость	Тело	Задаваемая плоскость
3D точка 1	Точка 3D	Первая точка
3D точка 2	Точка 3D	Вторая точка
3D точка 3	Точка 3D	Третья точка
3D точка 4	Точка 3D	Четвертая точка

Прототип команды: JQ Согласование Плоскость ; Точка_1 Точка_2 Точка_3 Точка_4 .

Пример 1:

Создать модель треугольникам по четырем моделям компланарных точек на эпюре Монжа.

Алгоритм "Главный"

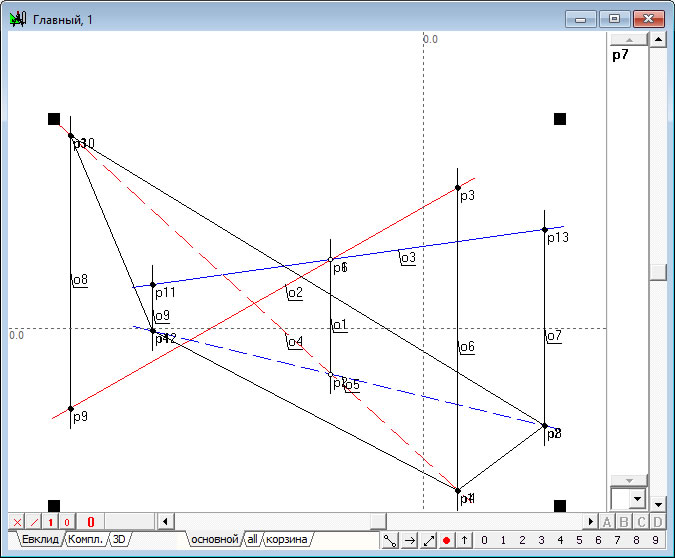
1		Прямая o9 задана координатами двух точек: X1= -237 , Y1= 125.5 , X2= -237 , Y2= 225.5 .
2		Прямая o8 задана координатами двух точек: X1= -309 , Y1= 106.5 , X2= -309 , Y2= 206.5 .
3		Прямая o7 задана координатами двух точек: X1= 106 , Y1= 83.5 , X2= 106 , Y2= 183.5 .
4		Прямая o6 задана координатами двух точек: X1= 30 , Y1= 140.5 , X2= 30 , Y2= 240.5 .
5		Прямая o1 задана координатами двух точек: X1= -81 , Y1= 60.5 , X2= -81 , Y2= -39.5 .
6		Точка p2 принадлежит объекту o1 с параметром принадлежности 1 .
7		Прямая o5 задана точкой p2 и углом -13.639052 к оси OX.
8		Точка p12 есть пересечение прямых o5 и o9 .
9		Точка p8 есть пересечение прямых o5 и o7 .
10		Прямая o4 задана точкой p2 и углом -42.455196 к оси OX.
11		Точка p10 есть пересечение прямых o4 и o8 .
12		Точка p4 есть пересечение прямых o4 и o6 .
13		Точка p1 принадлежит объекту o1 с параметром принадлежности 0 .
14		Прямая o3 задана точкой p1 и углом 8.0428942 к оси OX.
15		Точка p13 есть пересечение прямых o3 и o7 .
16		n2:0 p13 p8
17		Точка p11 есть пересечение прямых o3 и o9 .
18		n4:0 p11 p12
19		Точка p6 принадлежит объекту o3 с параметром принадлежности 0 .
20		Прямая o2 задана точкой p1 и углом 29.744881 к оси OX.
21		Точка p9 есть пересечение прямых o2 и o8 .
22		n3:0 p9 p10
23		Точка p3 есть пересечение прямых o2 и o6 .
24		n1:0 p3 p4
25		j1:0 n1 n2 n3 n4