Плоскость двумя прямыми

Отношение предназначено для задания плоского объекта на основе проекций двух пересекающихся прямых, расположенных в трехмерном пространстве.

Параметры	Типы объектов	Функциональное назначение параметров
Плоскость	Модель твердого тела	Определяемая плоскость
1-я пр. 1-й прямой	Прямая	Фронтальная проекция первой прямой
2-я пр. 1-й прямой	Прямая	Горизонтальная проекция первой прямой
1-я пр. 2-й прямой	Прямая	Фронтальная проекция второй прямой
2-я пр. 2-й прямой	Прямая	Горизонтальная проекция второй прямой

Прототип команды: JPL Согласование Плоскость ; 1-я_пр._1-й прямой 2-я_пр._1-й прямой 1-я_пр._2-й прямой 2-я_пр. 2-й_прямой .

Пример 1:

Построить и отобразить модель радикальной плоскости двух сфер, расположенных в трехмерном пространстве.

Алгоритм "Главный"

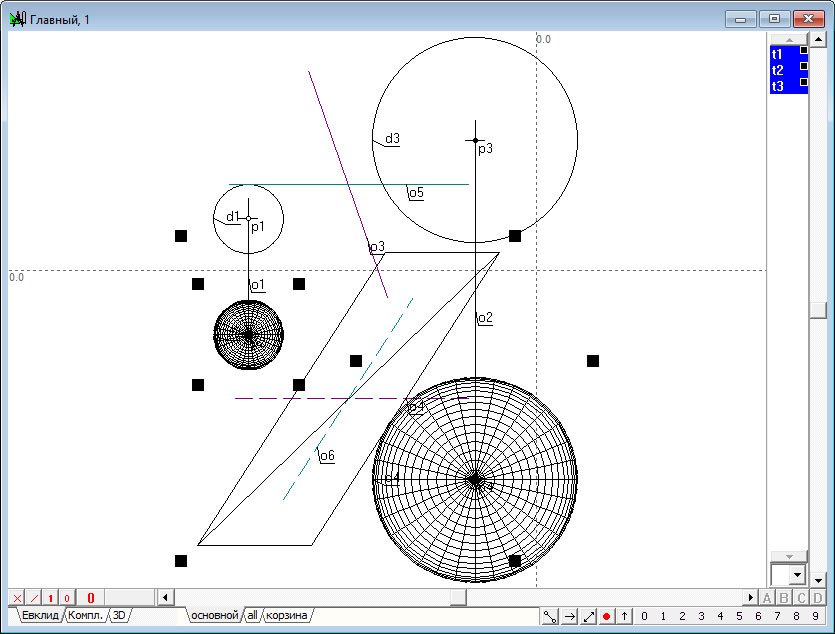
1		Прямая o1 задана координатами двух точек: X1= -248 , Y1= 44.5 , X2= -248 , Y2= -55.5 .
2		Величина t1 есть 30 .
3		Точка p1 принадлежит объекту o1 с параметром принадлежности 0 .
4		Окружность d1 задана центром p1 и радиусом t1 .
5		Точка p2 принадлежит объекту o1 с параметром принадлежности 1 .
6		Окружность d2 задана центром p2 и радиусом t1 .
7		Прямая o2 задана координатами двух точек: X1= -53 , Y1= 112.5 , X2= -53 , Y2= 12.5 .
8		Величина t2 есть 88.600226 .
9		Точка p4 принадлежит объекту o2 с параметром принадлежности 2.93 .
10		Окружность d4 задана центром p4 и радиусом t2 .
11		Модель сферы j1 по очеркам d1 и d2 .
12		Величина t3 есть 0 .
13		Точка p3 принадлежит объекту o2 с параметром принадлежности t3 .
14		Окружность d3 задана центром p3 и радиусом t2 .
15		Радикальная плоскость ( o3 - o4 ); ( o5 - o6 ) двух сфер ( d1 - d2 ); ( d3 - d4 ).
16		Модель сферы j2 по очеркам d3 и d4 .
17		Поскость в модель j3 по прямым ( o3 - o4 ), ( o5 - o6 ) в 3D.