|
||
| The task presented in this lesson is implemented in Simplex | ||
| 1 | The problem of spheres of Dandelin is one of the most beautiful and elegant geometric designs, which is easy to implement with relatively simple geometric objects in three-dimensional space. The problem statement asserts that it is possible to inscribe two spheres at arbitrary quadric and a plane, that intersects it. These spheres were named in honor of Dandelin. The main property of the task is that spheres touch the plane at points which are the foci of a conic - intersection line of the original quadric and a plane. The properties of spheres of Dandelin are usually considered on the basis of the analysis of metric characteristics included in the design of objects with application of affine geometry. However, in reality, the true nature of this problem is purely projective, and it is not well studied yet. Geometric design problem of spheres of Dandelin has much common items with the tasks of Apollonius and Fermat, that were discussed in the previous examples, at series of lessons on how to use Simplex for solving problems of constructive geometry. In this lesson, we will explore how to implement the geometric design of building spheres of Dandelin, and explore projective properties emerging in this task. This study will allow us to detect a geometric relationship that unites the objects of this construction and, therefore, to understand the design not only from the point of view of its implementation in actual space but in the space of imaginary images, and to declare the new task of finding such structures in spaces of higher dimensions. |
|
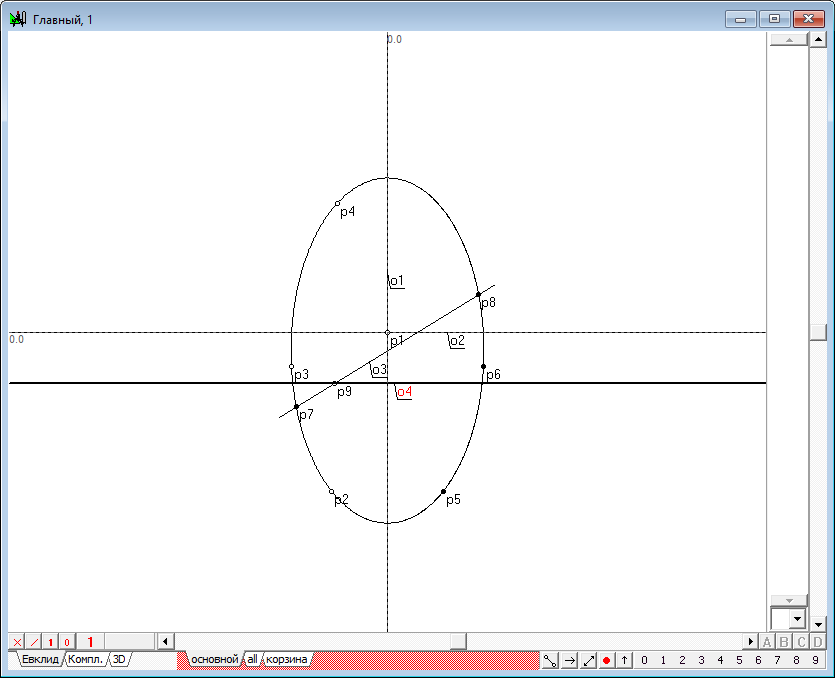
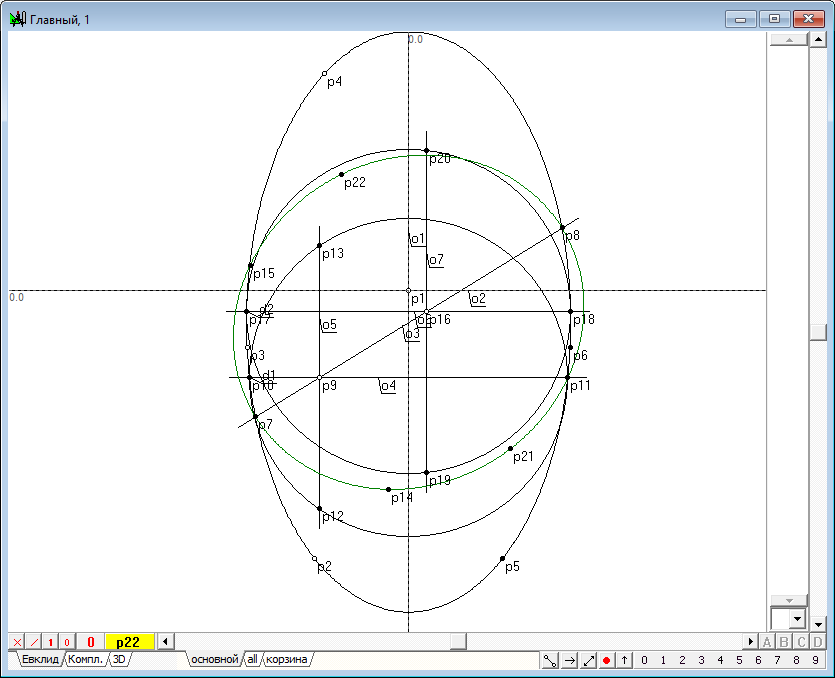
| 2 | Start to build the spheres of Dandelin. Define the source data is an arbitrary quadric and the section plane. Without loss of generality we implement this construction on the example of the ellipsoid by setting its frame rotation axis and the generatrix of the ellipse, which, however, we can easily transform into any conic. | |
| 3 | We will have two axes, one of which we assume the axis of the quadric. To do this, press the keyboard key with the Latin symbol z. Axis o1 will use as the axis of the quadric.
Рис. 1 |
|
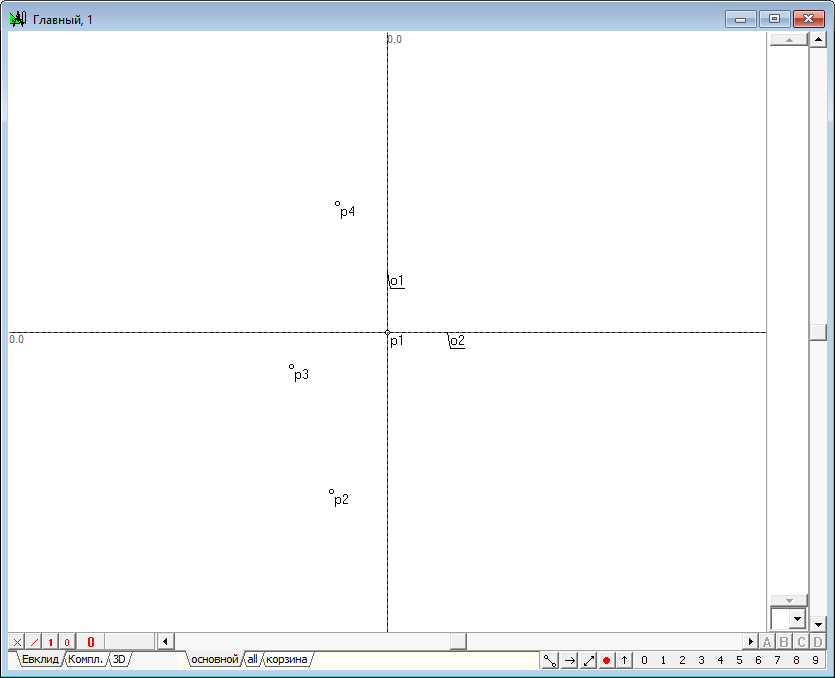
| 4 | Using a Free point tool, place the three points p2, p3 and p4 on the plane.
Рис. 2 |
|
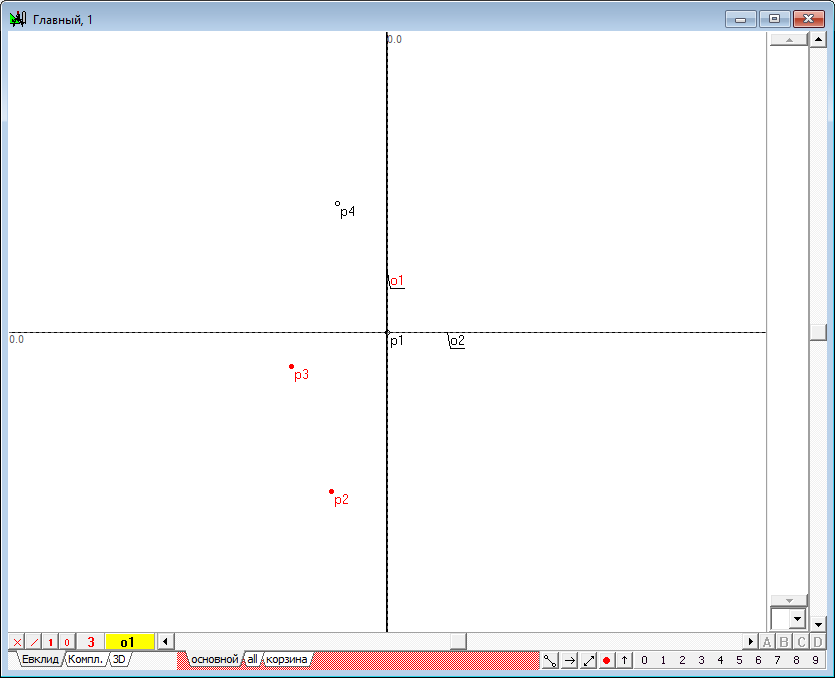
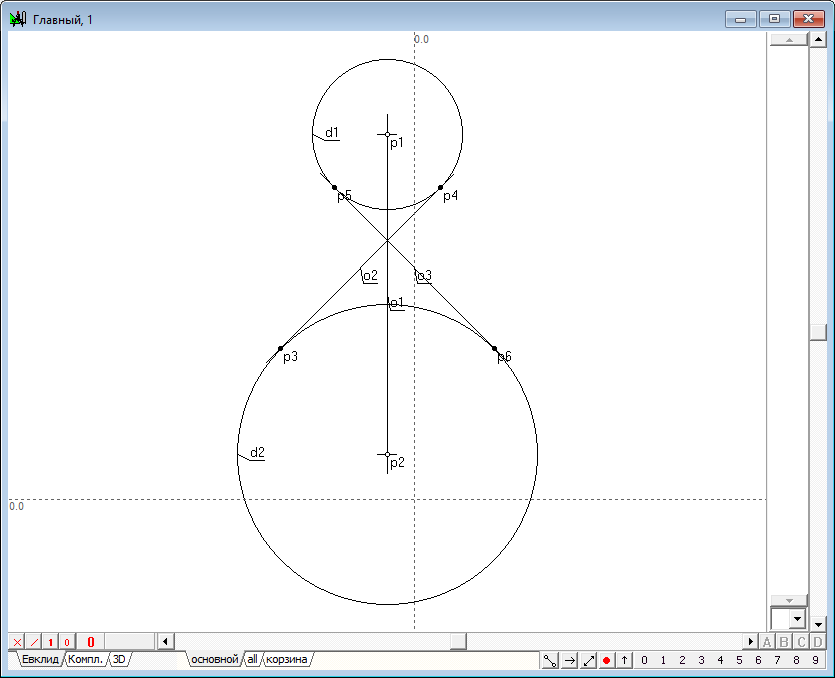
| 5 | Select two points (e.g., p2 and p3) and the axis o1.
Рис. 3 |
|
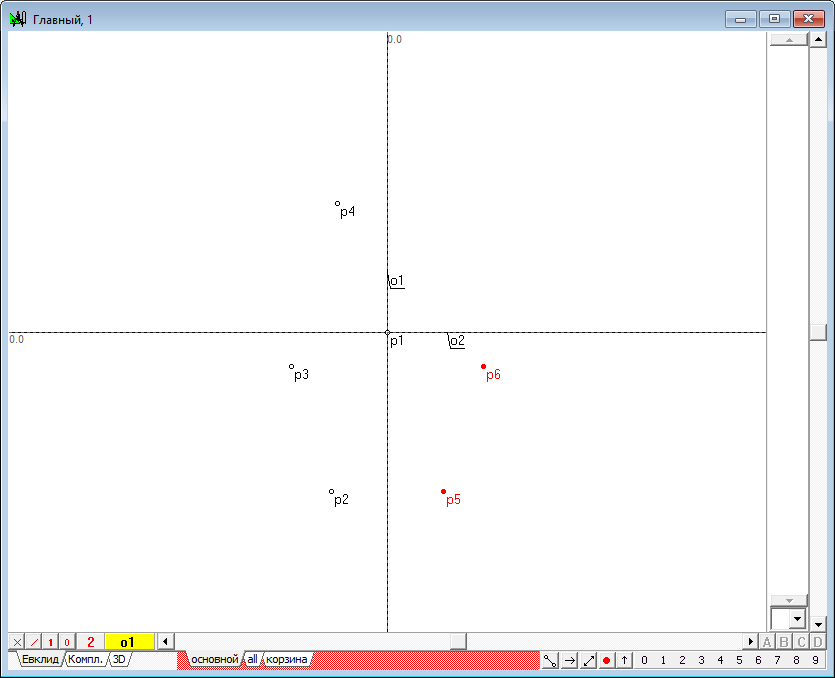
| 6 | Type on the key with Latin character x, to construct the points p5 and p6, that are symmetrical points p2 and p3 relative to the straight line o1.
Рис. 4 |
|
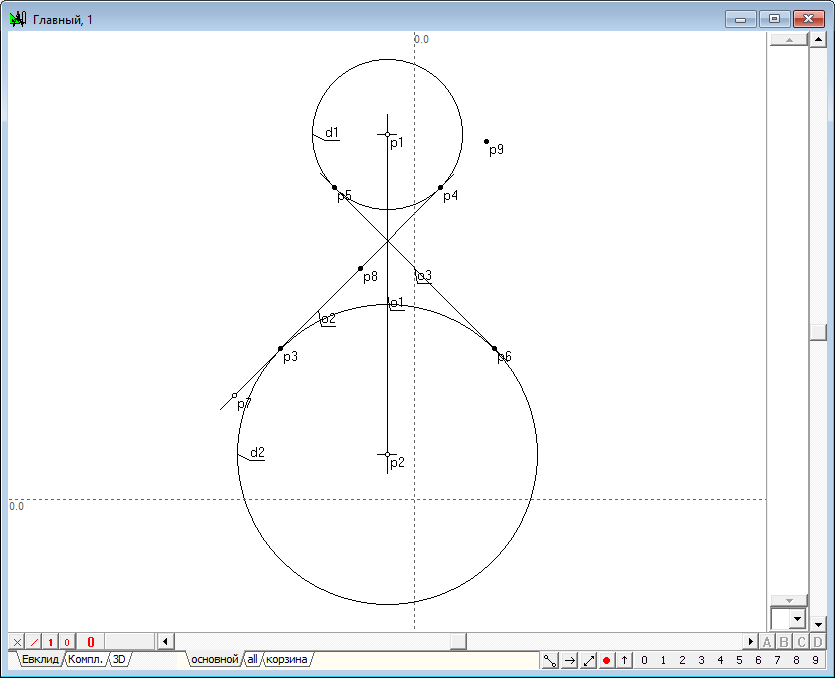
| 7 | Hold down the Shift key and add to the existing selection points p2, p3, and p4. Typing the key with Latin character y, construct conic y1.
Рис. 5 |
|
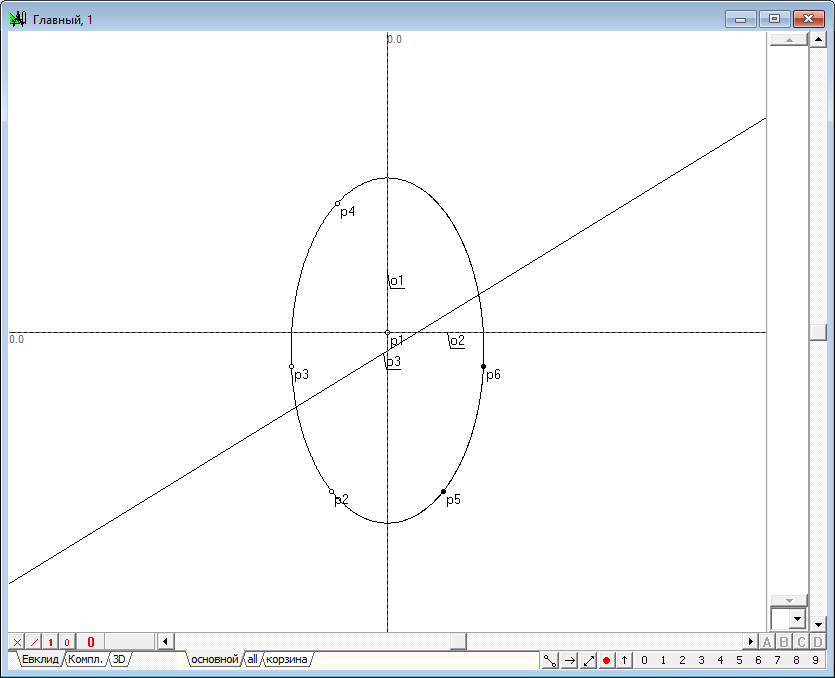
| 8 | Using the tool is Free line, produce the line o3, so that in the drawing it's clearly crosse the ellipse y1. This line will be used as a model of a plane occupying a projecting position and a secant quadric given axis and conical, with the aim of obtaining a section line.
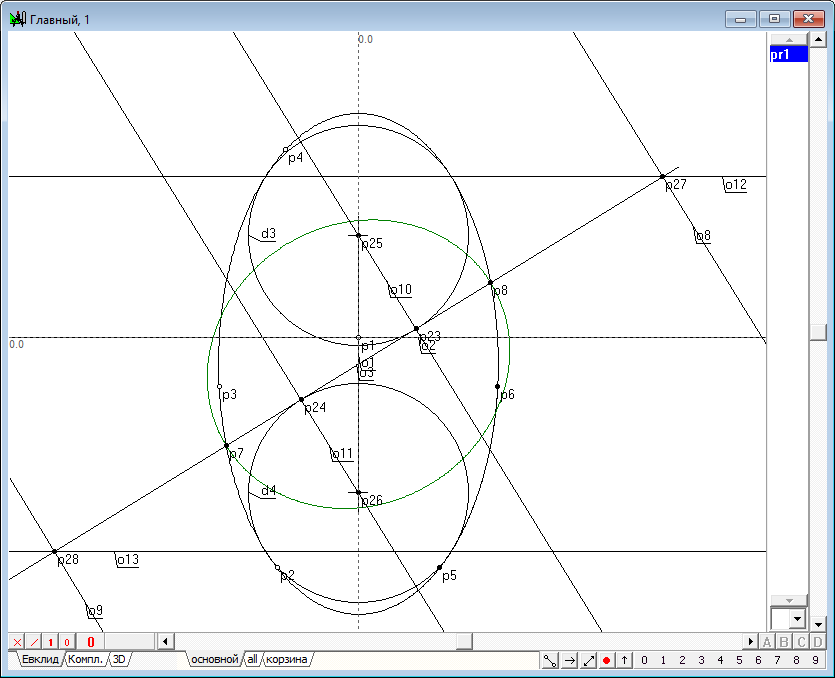
Рис. 6 |
|
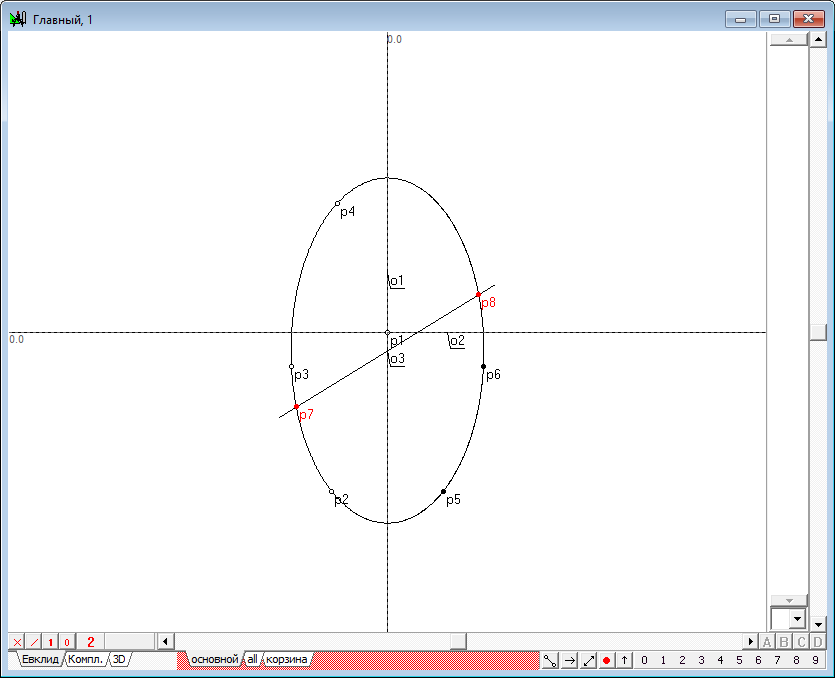
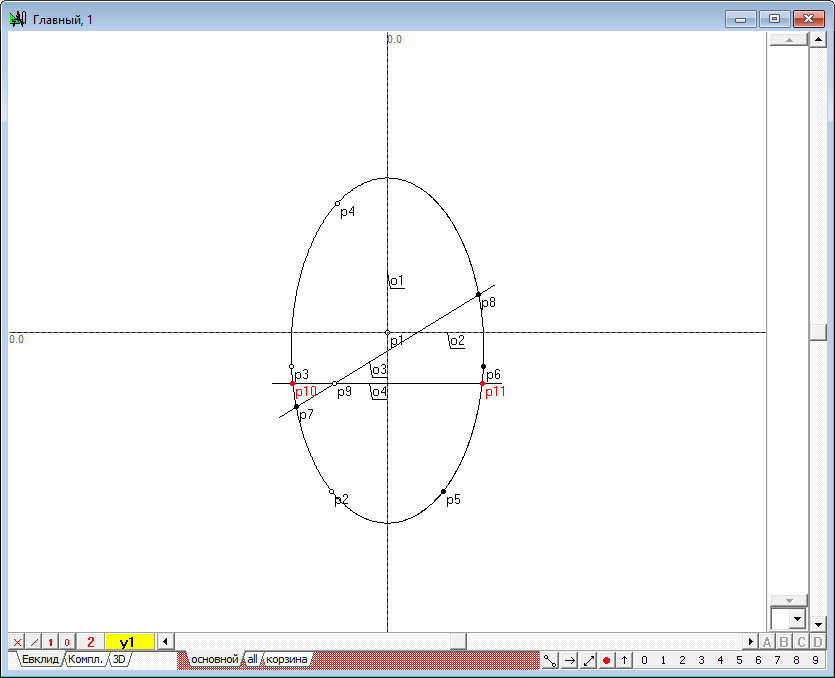
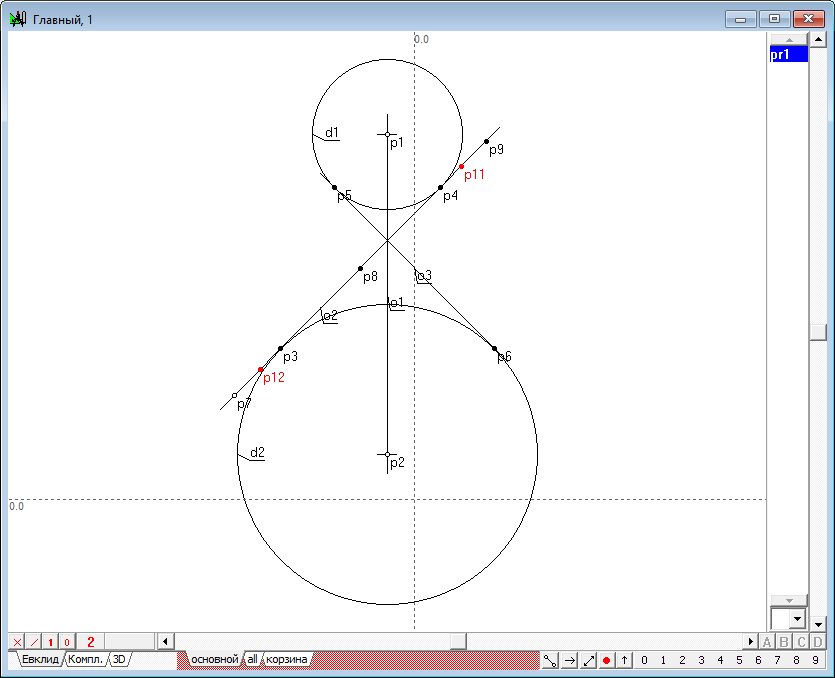
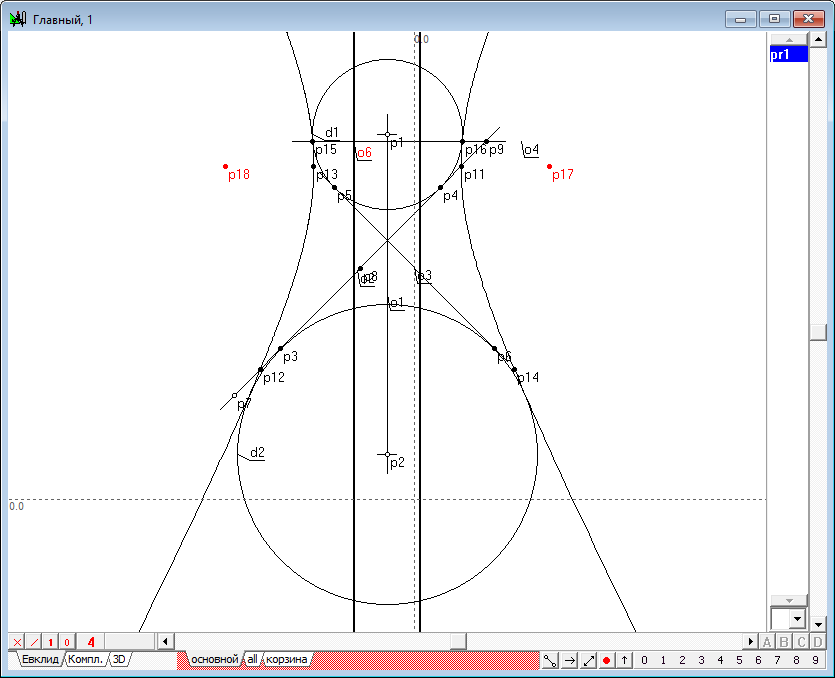
| 9 | It is well known that such line should be a conic, so to define it we need to find at least five points belonging to the conic. To do this we will solve the problem of finding such points on the surface of the quadric. Two of the required five points is easy to find. It is necessary to find the intersection points of a line conic o3 and y1. To get them, select the objects o3 and y1, and typing the key with Latin character p, we construct the points p7 and p8.
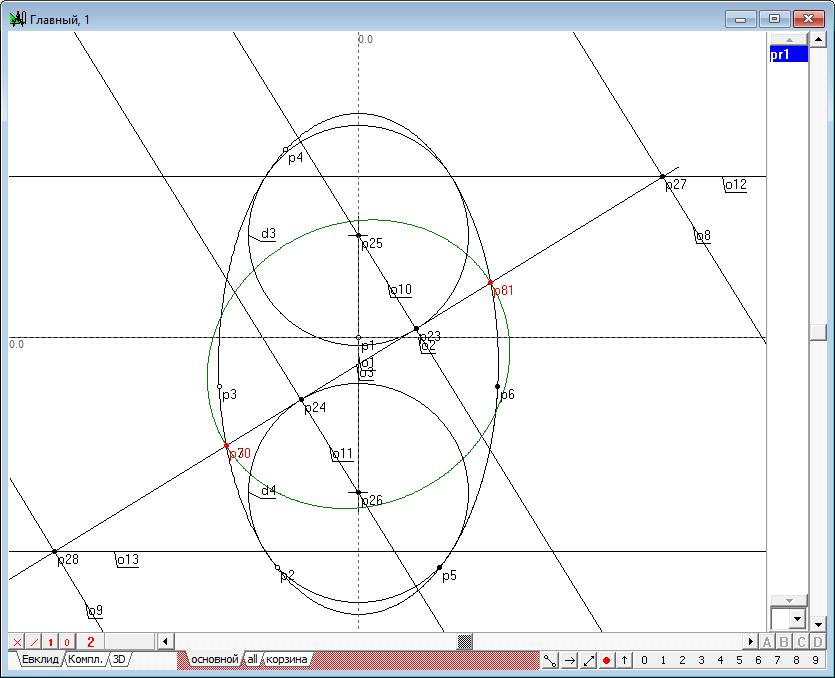
Рис. 7 |
|
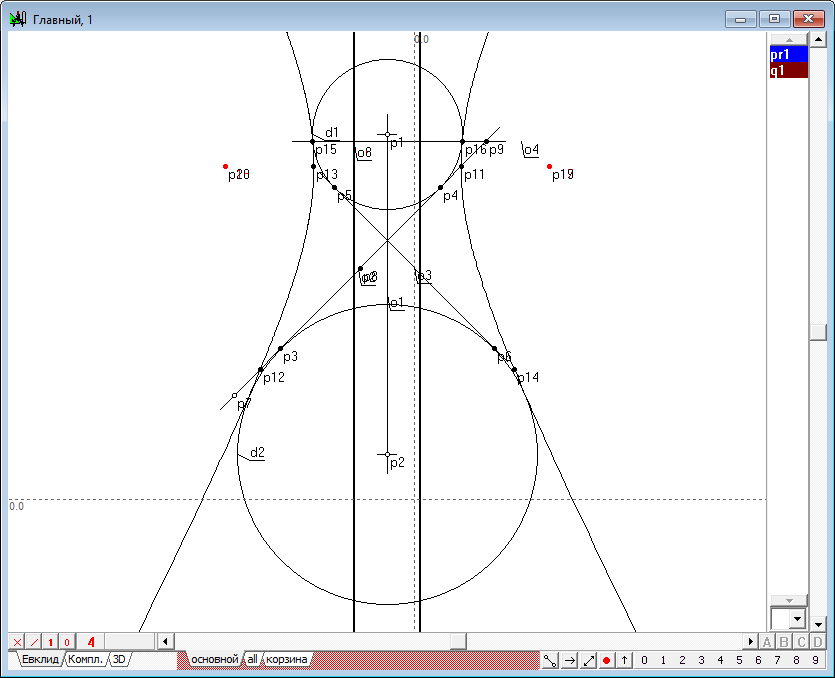
| 10 | To retrieve the remaining points use the fact that the plane perpendicular to the axis of the quadric intersects the quadric in a circle twice. First, take off the highlighting of objects. Then hold down the Ctrl key, set the cursor in а such position that it is located somewhere above the image of the straight line o3 and click the left mouse button. This will allow you to assign point p9 to line o3. We will use this point p9 to position extra section plane, which we construct perpendicular to the axis of the quadric.
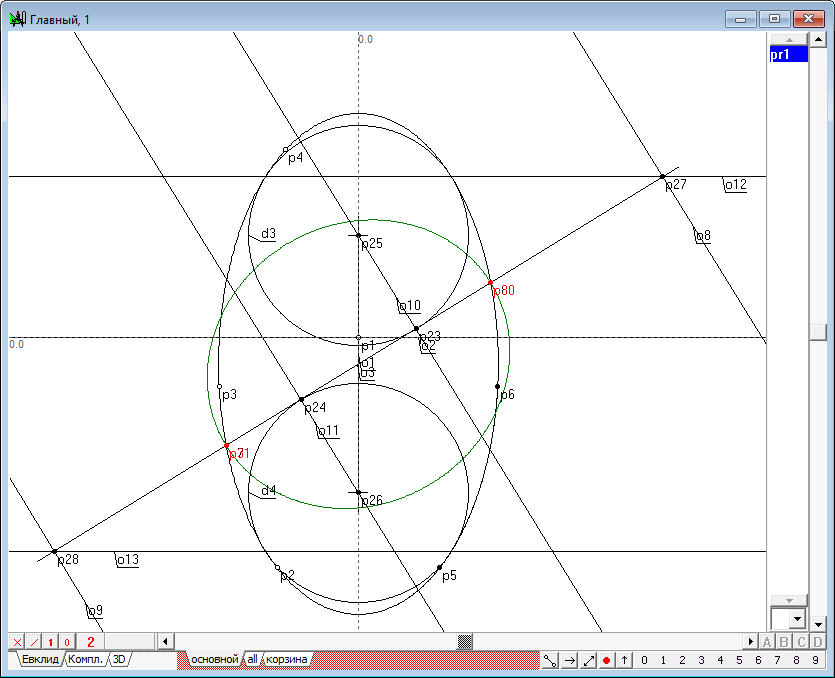
Рис. 8 |
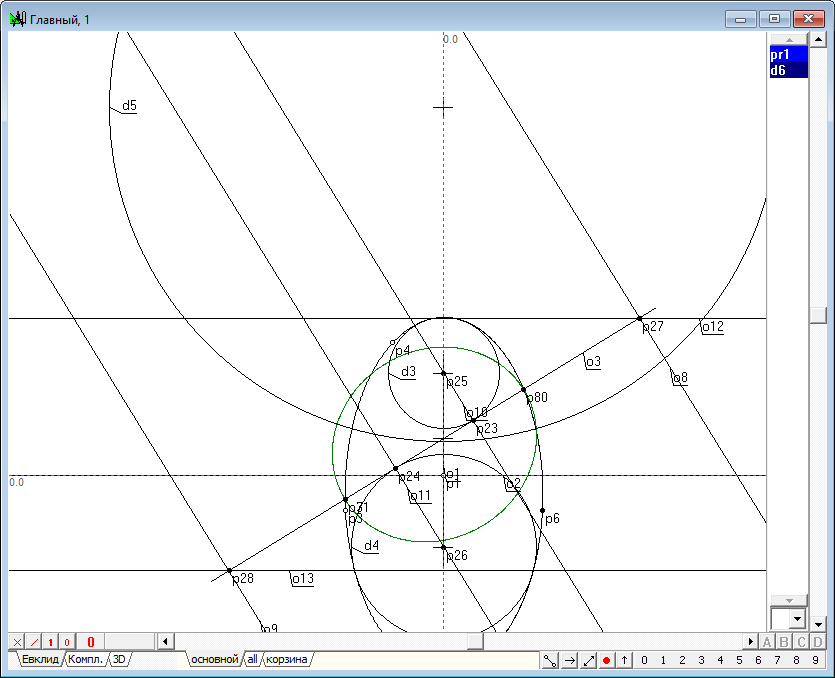
|
| 11 | Select point p9 and type on the key with the Latin character h, draw a horizontal line o4, simulating a plane.
Рис. 9 |
|
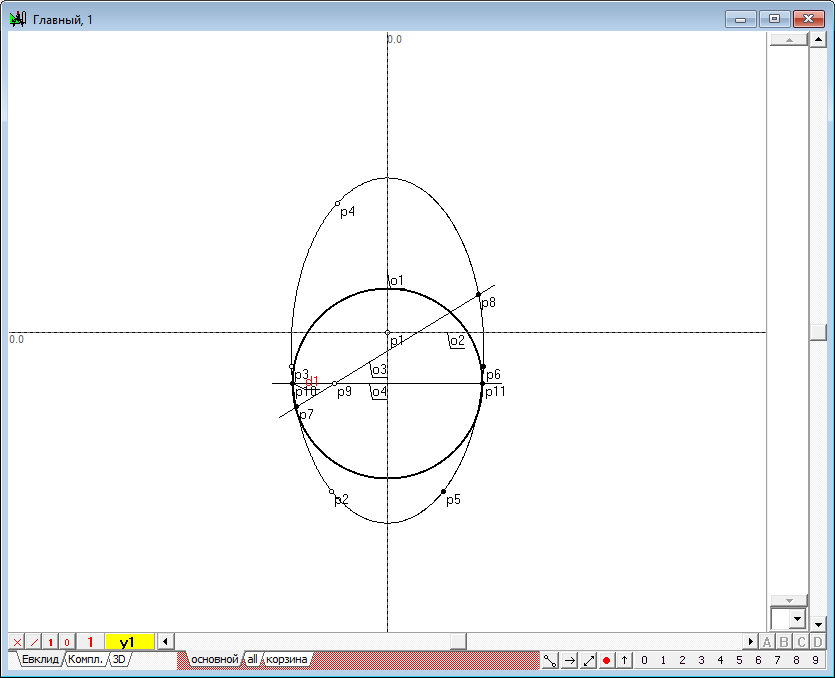
| 12 | Hold down the Shift key and add conic y1 to the selection and press on the key with Latin character p. The result points p10 and p11 appear, to determine the diameter of the circle - a result of the additional cross-section of plane with the original quadric.
Рис. 10 |
|
| 13 | Points p10 and p11 specify the cut - frontal image of this circle. To obtain a horizontal view (of the circle d1, depicted in life-size), press the key with a Latin symbol D (upper case).
Рис. 11 |
|
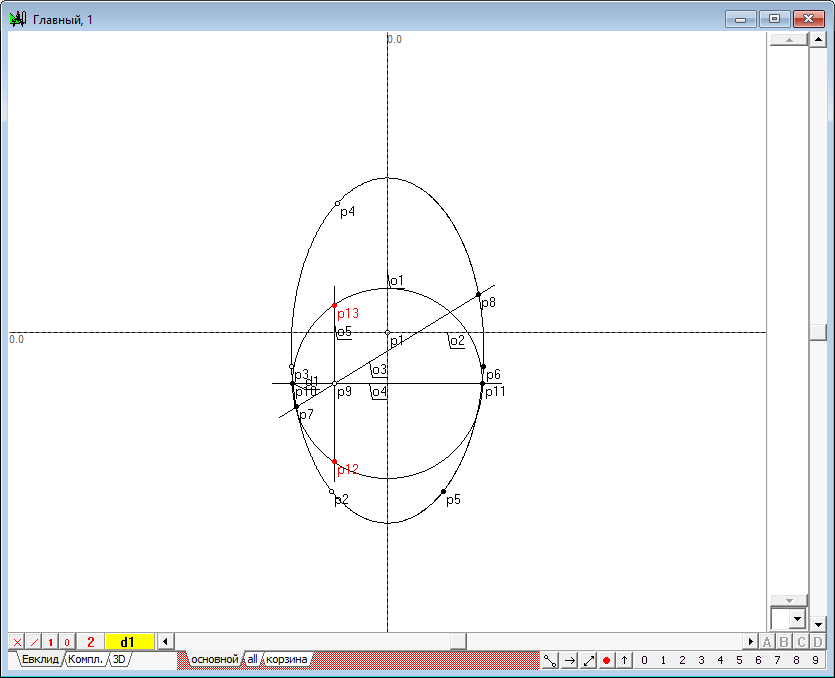
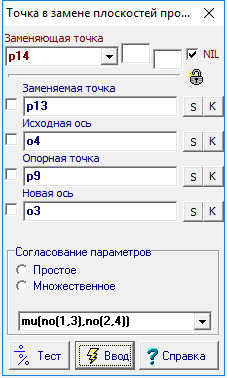
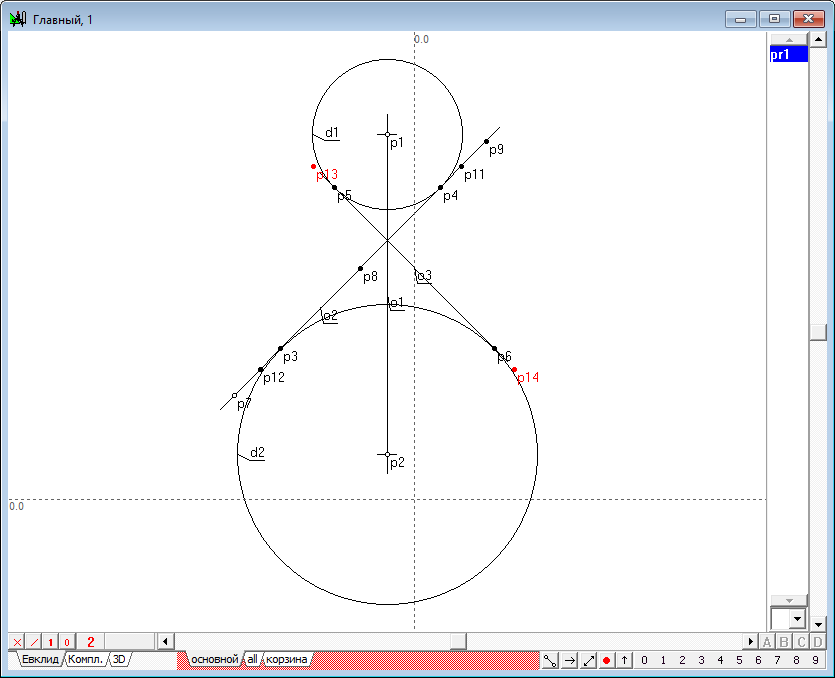
| 14 | Construct two points that are common to both circle and conic in the present additional orthogonal plane. Frontal projection of these points are known - they are modeled by point p9. It is easy to find Horizontal projection, if movethrough the point p9 vertically to find the point of intersection with a circle d1. To to this select point p9 and type on the key with the Latin symbol v. Then hold down the Shift key and add the circle d1 to the selection, type on the key with Latin character p, get the initial point p12 and p13.
Рис. 12 |
|
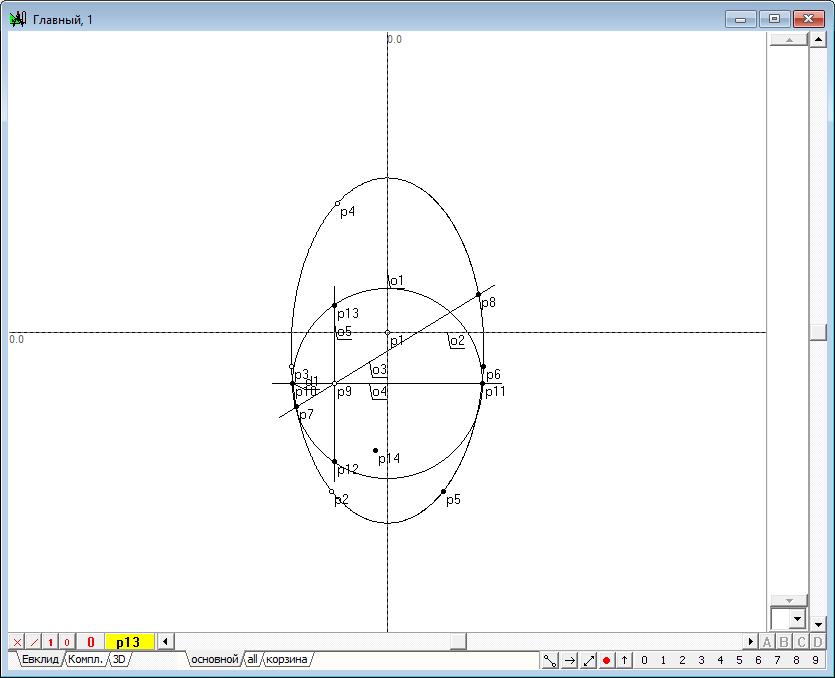
| 15 | Now our task is to built the image of line of the original plane with the quadric section. Front and degenerative image of it, is know for us: it is the length between points p7 and p8. Therefore, we should recover an additional orthogonal projection of this line, taking the new transform axis line o3, and to rely upon the transition to the new system of projections from the "old" will be using the straight line o4. Call Point function in replacement of the planes of projections and fill in the dialog box, defining the input parameters of this function as indicated in figure 13.
Рис. 13 |
|
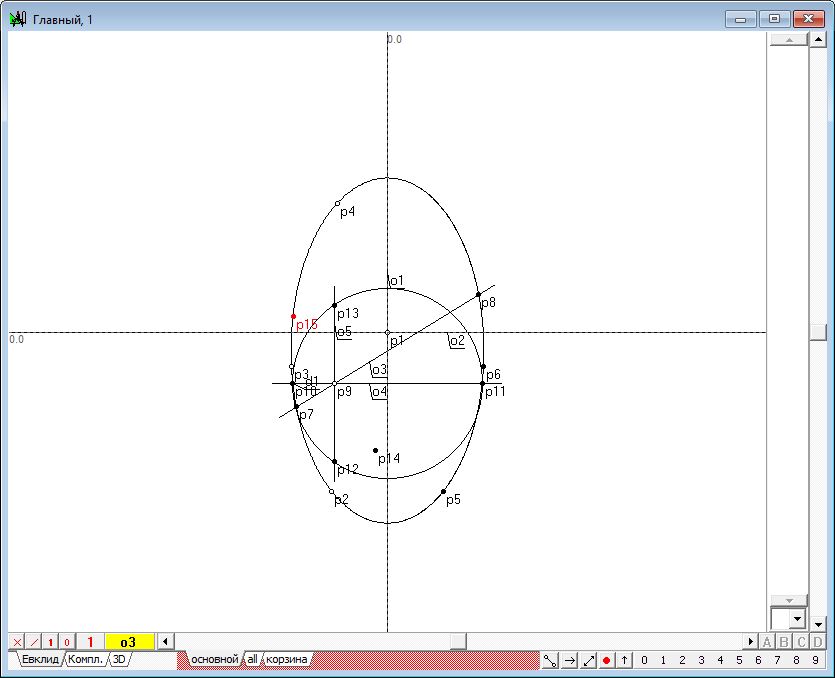
| 16 | After clicking on the Enter button, we get the point p14 - the one of those points that we need to determine to build the true value of the desired conic.
Рис. 14 |
|
| 17 | It is not difficult to build points p15, p14 symmetrical in relation to the axis o3. To do this highlight consistently the point p14 and the straight line o3 and press the key with the Latin character x.
Рис. 15 |
|
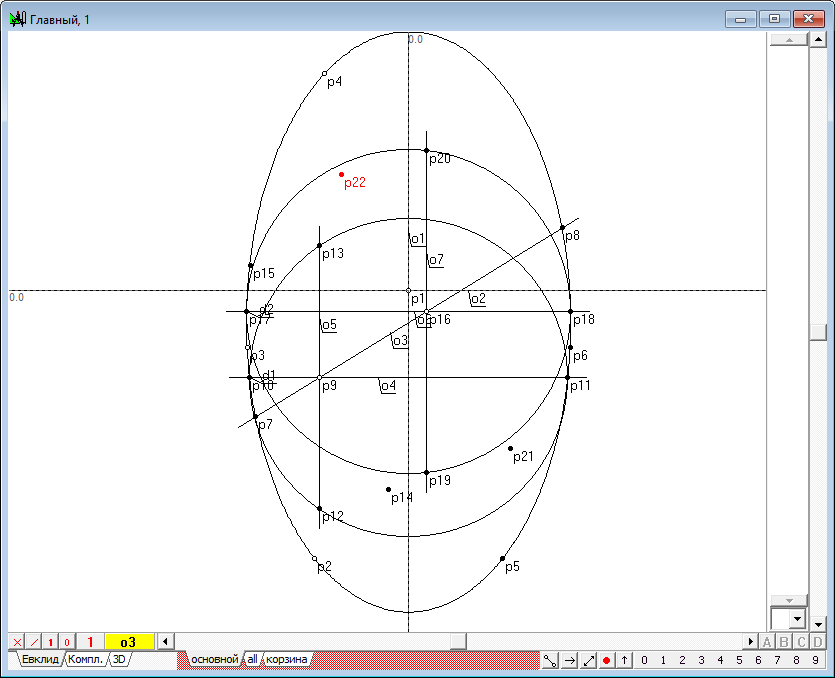
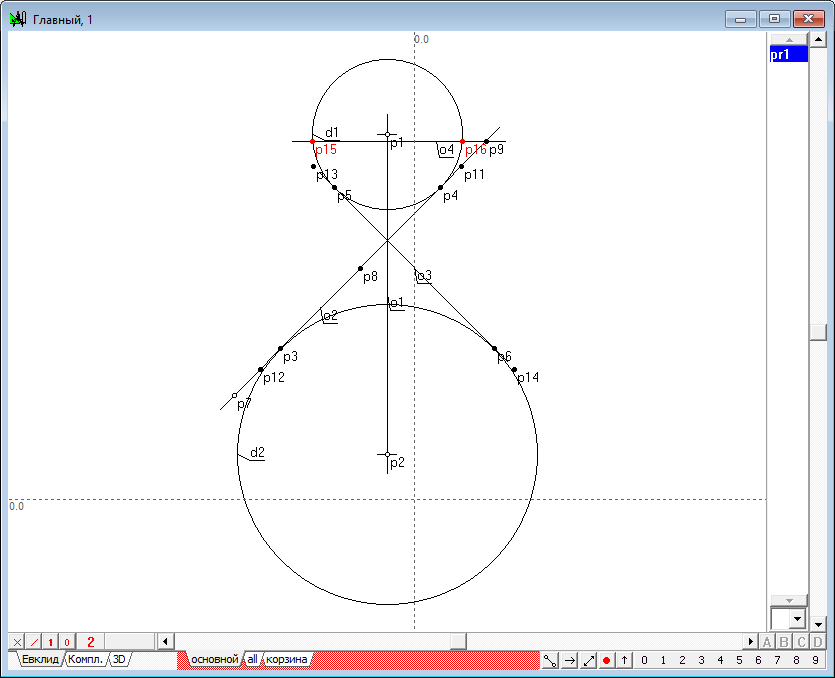
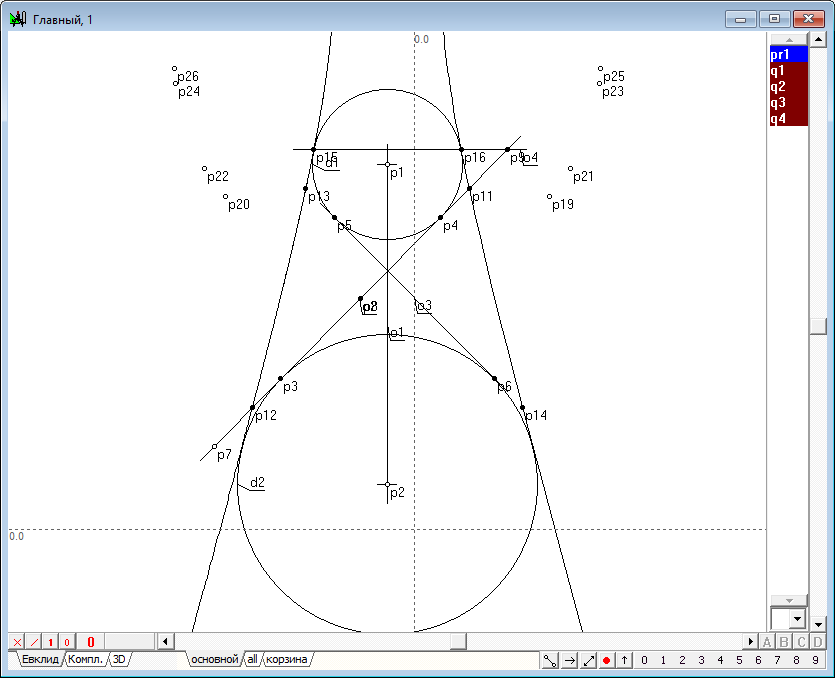
| 18 | So, we've got four points for the future conic. Since a conic is uniquely built in five points, still one point is to be defined. Thus, placing similar point p9 on the straight another point p16, repeat the just completed build once more. As a result, will receive points p21 and p22, one of which is redundant and can be used for visual verification of the fact that all constructed points do lie on the required conic.
Рис. 16 |
|
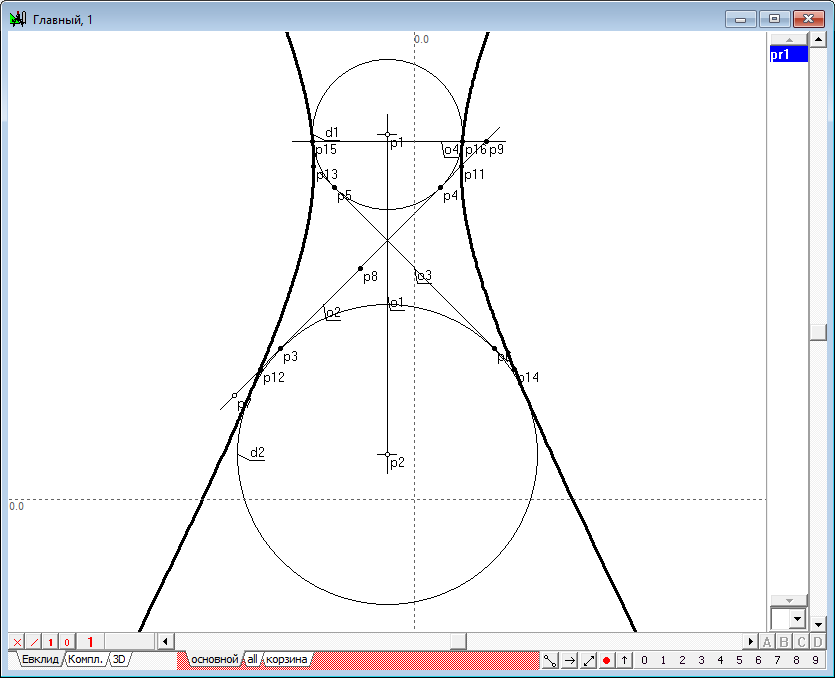
| 19 | Let's construct the required conic y2. To do this, select the points p21, p8, p14, p15 and p7 and click on the keyboard with Latin character y.
Рис. 17 |
|
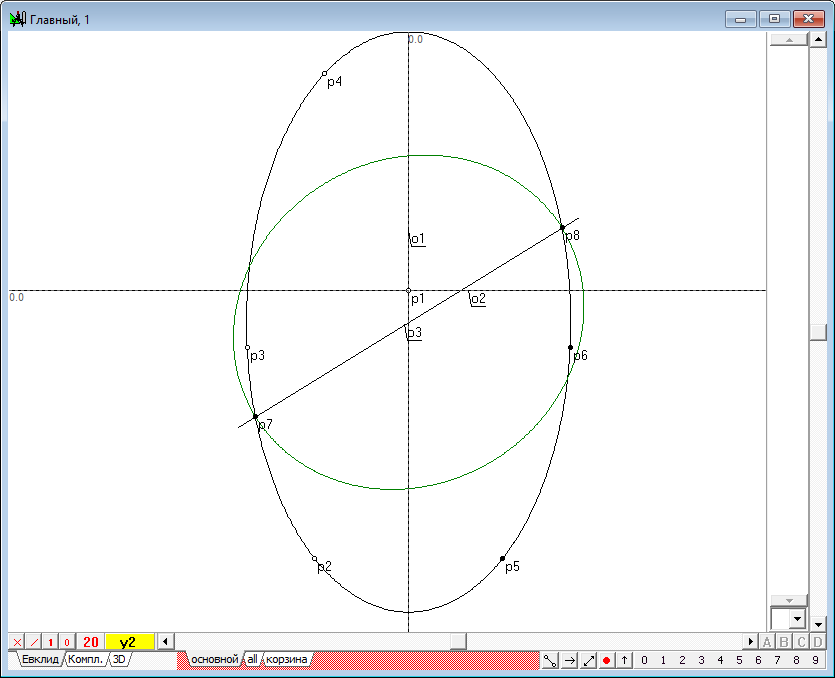
| 20 | Because some items of our construction have a subsidiary meaning and not necessary for the subsequent solution of the problem, it makes sense to move images of helper objects to the layer Trash. To do this, select all those objects that we no longer needed, and press the key with the symbol \. Such separation is easy to perform, if you allocate only point p9 and p16, and then, triggering a right-click context menu to choose the selection mode With the descendants. The result will select all those objects that directly depend on the points p9 and p16. However, among these objects there will be the desired conic. It will still neccessary for us. To exclude conic y2 from the selection hold on the Shift key, move the cursor so it is located above the image conic y2, and click the left mouse button. The selection of a conic will be disabled, while all other objects to be transferred to the layer Trash, will remain in the selection .
Рис. 18 |
|
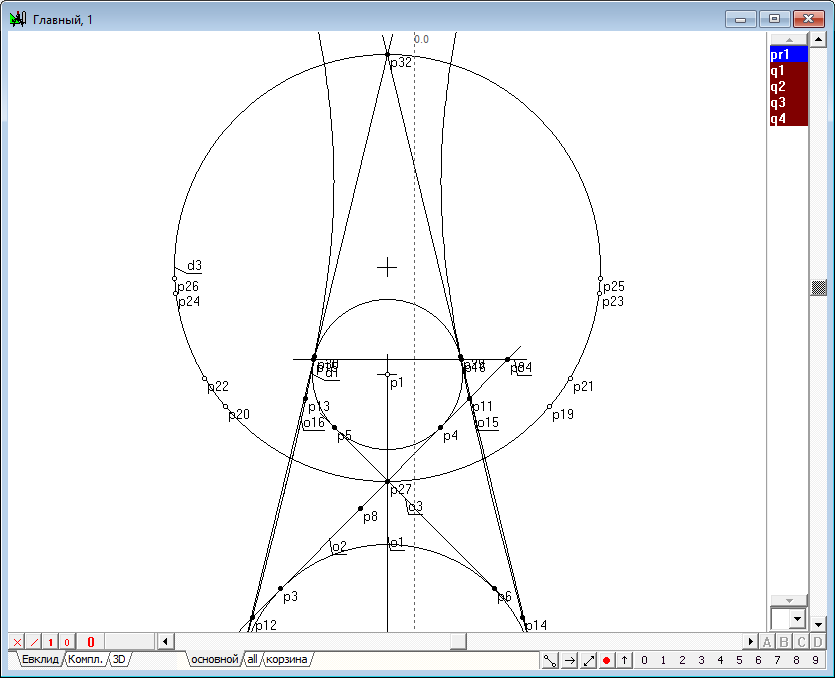
| 21 | So, conic is built. Find its foci and directrix. To do this, select conic and click on the key with Latin character f.
Рис. 19 |
|
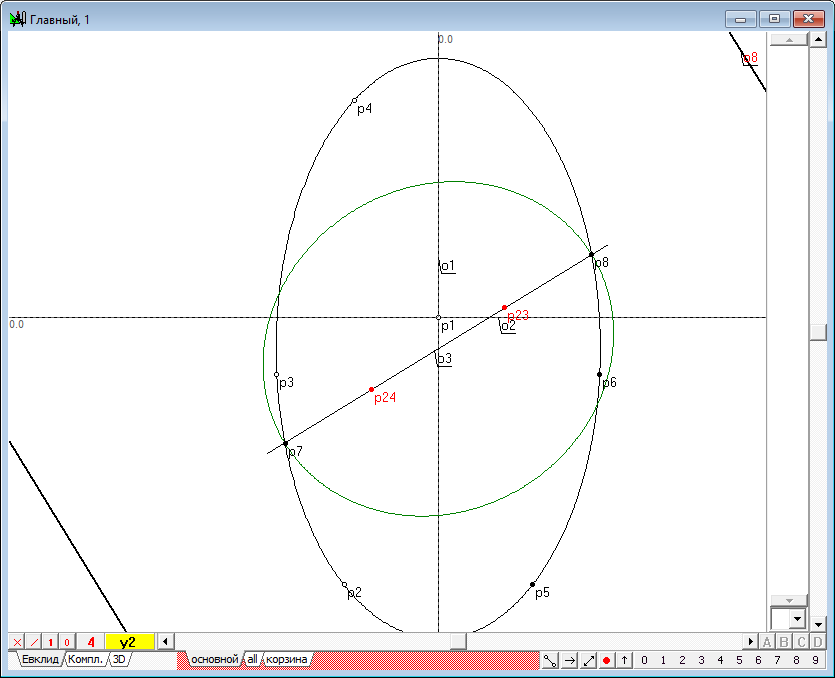
| 22 | It is clear that the cents of Dandelin spheres must lie on the axis of the original quadric. Assigne two perpendiculars to the line o3 passing the points p23 and p24. To do this, select the first point p23 and the straight line o3 and type on the key with Latin character o. Get a line of o10. Then same steps repeat applying them to the point p24 and get the line o11.
Рис. 20 |
|
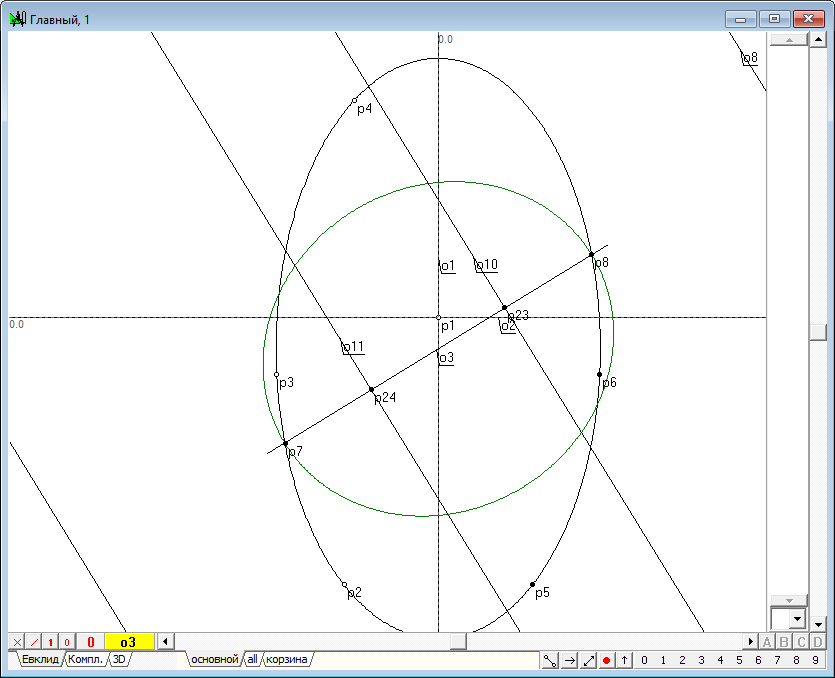
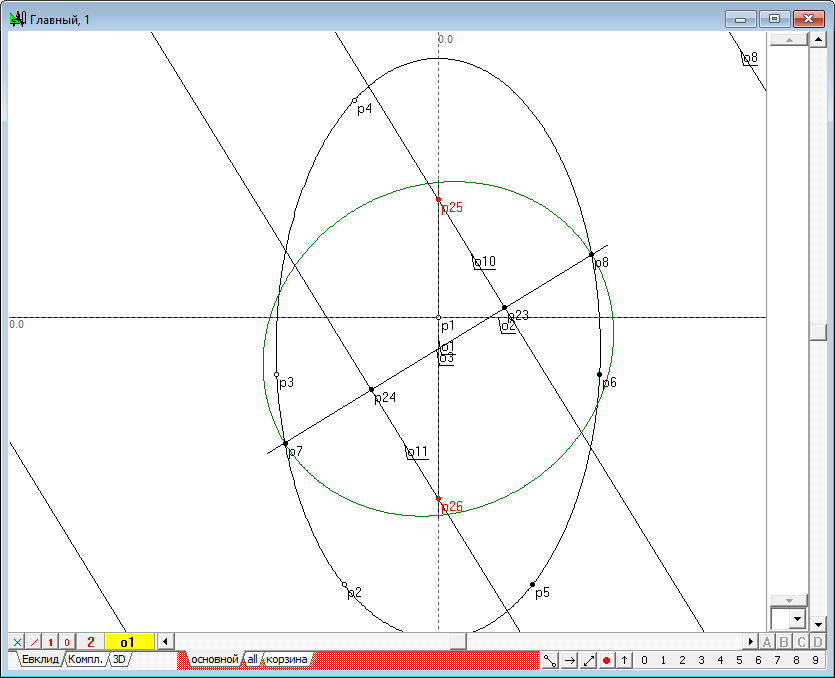
| 23 | Highlight sequentially the line o10, o11 and o1 and click on the key with Latin character p. We get the centers of the spheres of Dandelin - points p25 and p26.
Рис. 21 |
|
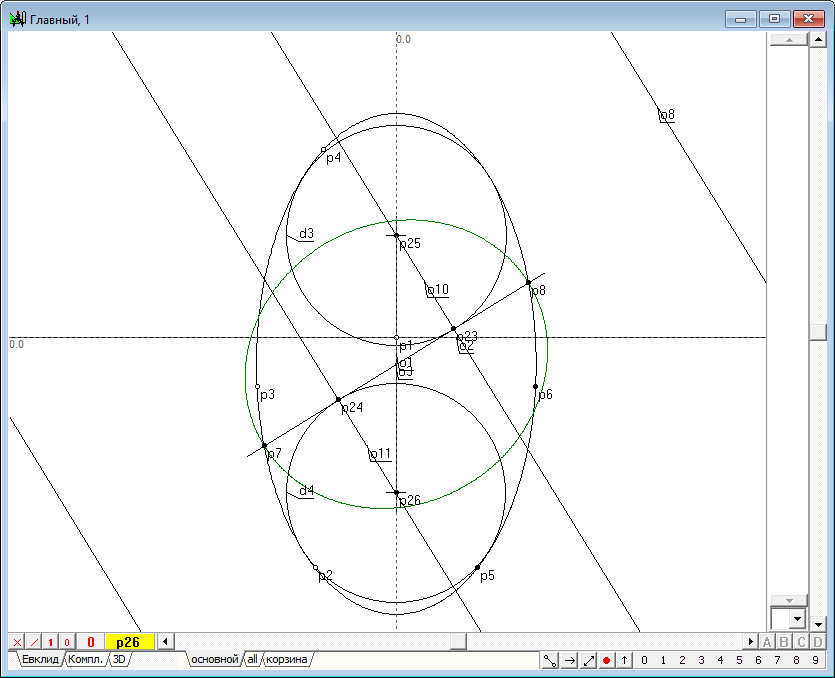
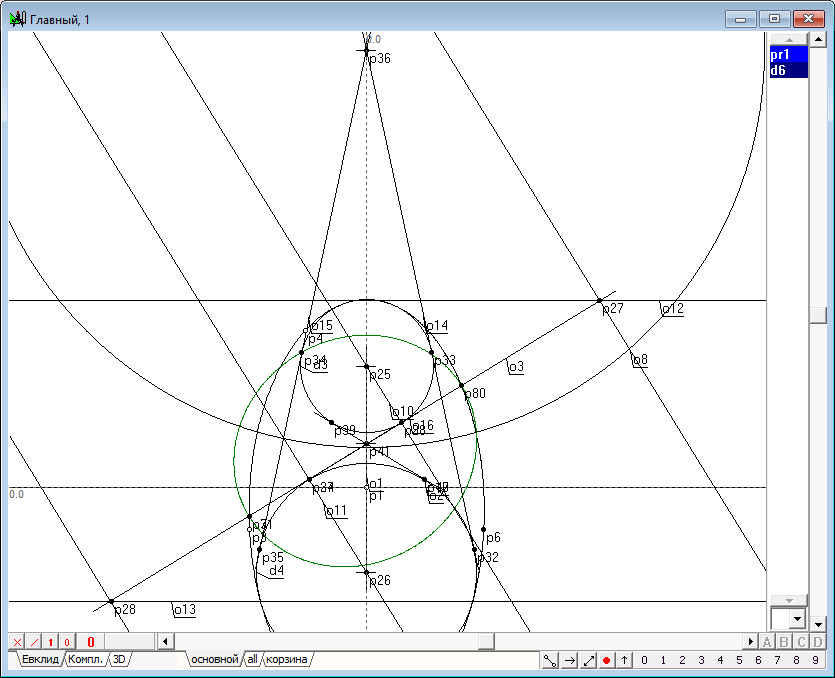
| 24 | Now we can build and the outlines of spheres themselves. Highlight sequentially the points p23 and p25 and click on the key with Latin character d. Get a circle d3. Highlight sequentially the points p24 and p26, and click on the key with Latin character d. Get a circle d4. Circumference d3 and d4 - are outlines generatrix of the forming spheres of Dandelin in the frontal projection. Indeed we have seen touch these spheres to the generatrix of the initial quadric to the source plane.
Рис. 22 |
|
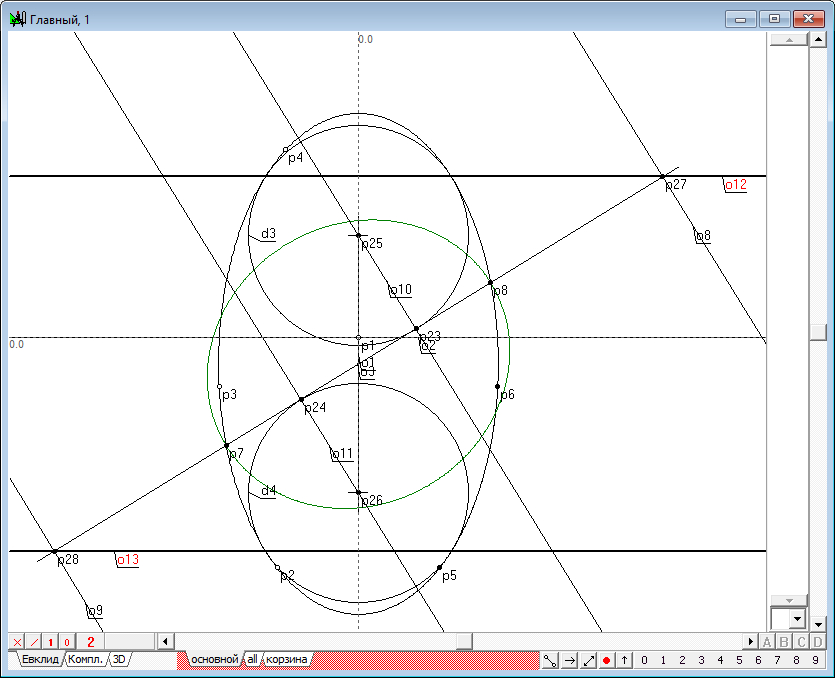
| 25 | Sphere of Dandelin are built. Now proceed to the study of projective properties of the obtained constrcutive. Find the point of intersection of directrix o8 and o9 y2 conic with a straight line o3.To do this highlight these lines and press successively on thekey with the Latin character p. Get points p27 and p28. Then, without selection deactivating press the key with the Latin character h, which will allow us to obtain two horizontal lines o12 and o13. Note that these lines cross the outlines of spheres of Dandelin and the original conic at the points of tangency, and in three dimensions space these lines set the circumference of the touch areas of Dandelin and the original quadric.
Рис. 23 |
|
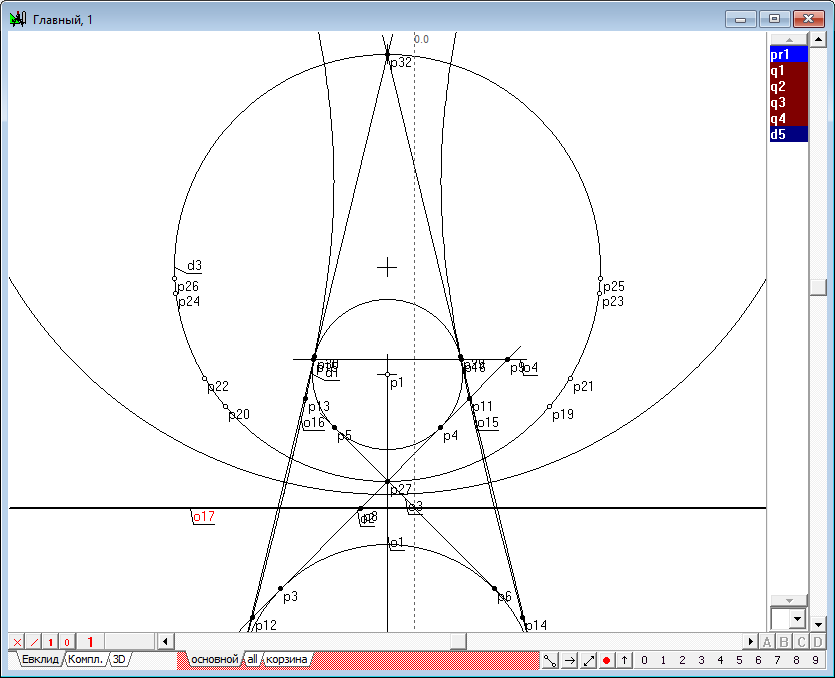
| 26 | It is known that conic induces involution in a straight line. We define this involution by an Involution function from a conic in a straight line.
Рис. 24
Рис. 25 |
|
| 27 | It is also known that the dual points of this involution are the points of intersection of this line with conic, and under the points of intersection they understood as valid points and imaginary. Will check it out. Select the label involution pr1 and press on the key with Latin character p. Get the two points coinciding with the points p7 and p8.
Рис. 26 |
|
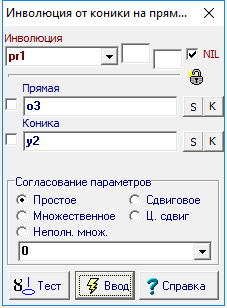
| 28 | Cancel the last two steps by twice clicking on Ctrl+Z. Now we define the involution differently. Hold down the Shift key, highlight consistently the point p28, p24, p23 and p27, and then add line o3 to the selection, then press the key with the Latin character k. After the definition of involution pr1 press on the key with Latin character p to get the dual points of this involution. It is easy to verify that in this case the dual points of the involution coincide with the points of intersection of a straight line o3 and conic y2.
Рис. 27 |
|
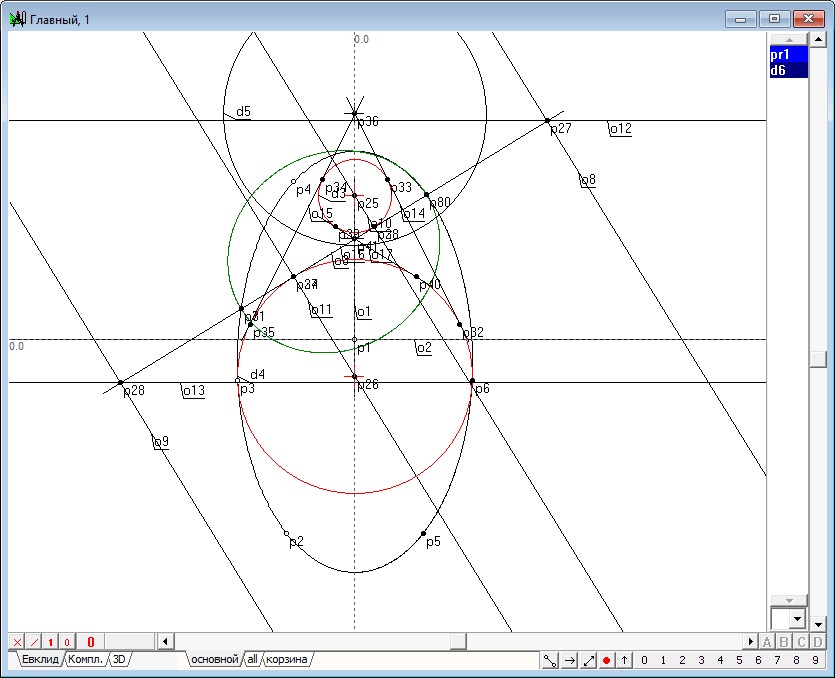
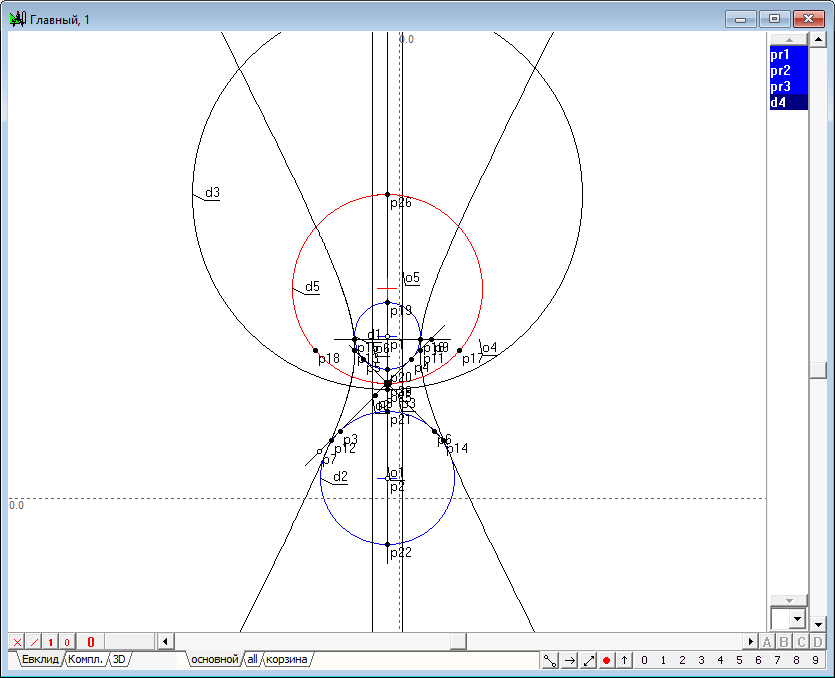
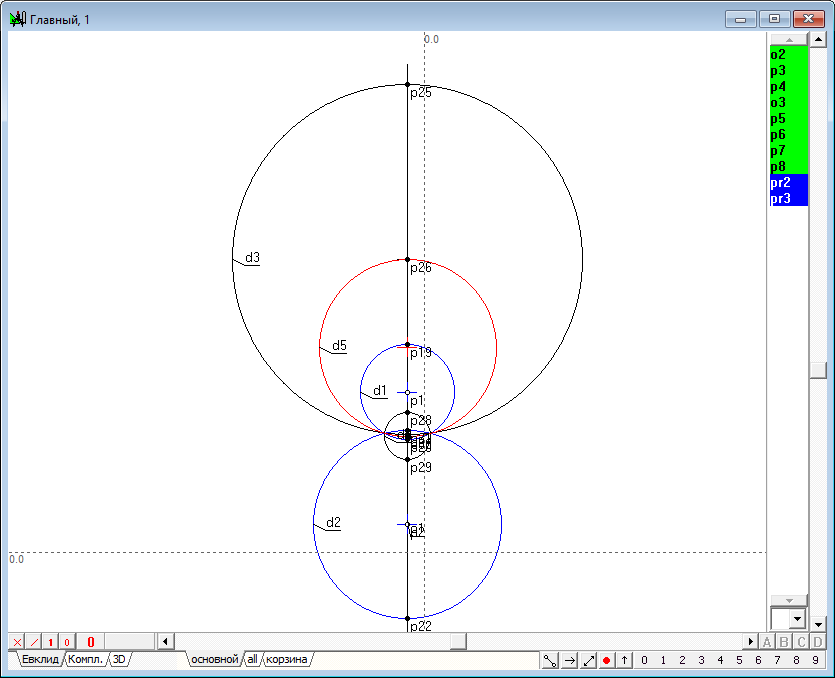
| 29 | Build a spheres of inversion for found spheres of Dandelin. Since in our example the spheres of Dandelin do not intersect each other, then one of the spheres of the inversion is valid and the second is imaginary. Select the circle d3 and d4 and click on the key with Latin character R (in uppercase). Get the circumference of d5 and d6.
Рис. 28 |
|
| 30 | The centers of the two spheres of inversion are located at the vertices of two cones are tangent to the spheres of Dandelin. To check this fact, construct a common tangent to the circles, outlines of spheres of Dandelin. Select the circle d3 and d4 and click on the keys sequentially on the o, 8, p. Then again, select the circle and press on the keys sequentially on the O (uppercase), 8, p. Get outlines of the two cones described around two spheres. The vertices of the cones p36 and p41 coincide with the centers of the inversion spheres - one real and one imaginary.
Рис. 29 |
|
| 31 | I would like to note that we found a manifestation of the projective properties of geometric designs tasks of Dandelin in this construction. Examine some of their properties in more detail. Move the line o3 withshaper straight up, parallel to its former position and fix it in this position, in which the line o12 cease to constitute a real points of intersection with the generatrix of the quadric - conic y1.
Рис. 30 |
|
| 32 | We find, however, that the outline of the sphere is a circle d3 is real, however, clear of contact with the outline of the quadric in the drawing is not traced. However, because of the generality of the constructs it can be argued that the scope, the simulated front-essay - circle in d3 exists and it is a sphere of Dandelin. This sphere has an imaginary touch with the original quadric. The sphere and the quadric are elements of a bundle of quadrics, defined by an imaginary circle defining the bundle. Diametral points of the circle are easy to find if you build imaginary point of intersection of the circle and straight d3 o12, and also the imaginary point of intersection of conic and straight line y1 o12. It is also easy to verify that the coordinates of these points correspond to each other. These builds it is recommended to perform independently and ensure that they give the same results. |
|
| 33 | As it can be seen from the construction shown in figure, the real sphere of Dandelin exists even in the case when the plane roses above its center.
Рис. 31
Рис. 32 |
|
| 34 | Now solve the problem, the opposite in its wording to the newly considered. Let given two arbitrary spheres. To construct a quadric for which these spheres are spheres of Dandelin. Show that the quadric satisfying this condition form a one-parameter bundle and examine some properties of this beam. We define two arbitrary spheres. Construct a straight line bearing at two points, clicking on the key with the Latin symbol V (upper case).
Рис. 33 |
|
| 35 | Leave in the selecton only the point p1 and press on the key with Latin character d. Get a circle d1 with center p1 and radius defined by the current cursor position. Construct similarly the circumference of d2 with center at p2.
Рис. 34 |
|
| 36 | We will hold on the line tangent to the circles d1 and d2. To do this, select the circle and press on the keyboard with the Latin symbol O (uppercase).
Рис. 35 |
|
| 37 | Lines o2 and o3 can be understood as the outline generatrix of a cone tangent to the original sphere. We assume the line o2 is also the projection of the plane of the desired quadric, occupying a projecting position. This means that the conic - section the plane of the desired quadric will be shown in the form of a segment of a o2 and the foci of this conic is nothing but as points p3 and p4. Ask for direct o3 control point and assume that the point of geometrical intersection of the directrix of a conic with the axis o2. Then it will not be difficult to find the point of intersection of the second headmistress with conical. Perform the following construction: - hold down the Ctrl key and click the left mouse button, that will place a point p7 on the straight line o2; - highlight the points p3 and p4 and press c to build a center of symmetry of these points; - highlight the sequence of points p7 and p8 or pressing the key with the Latin character x find the point p9 is the intersection of the second principal axis of a conic.
Рис. 36 |
|
| 38 | As we have seen in the previous problem, an outline of the desired quadric must pass through the dual points of the involution specified directorially and the focal points on the line. In order to find them, select successively the points p7, p3, p4 and p9, as well as o2 direct, press on the key with Latin character k to determine the involution pr1 and following this key with a Latin symbol p, which will find the double points of the involution pr1 - points p11 and p12.
Рис. 37 |
|
| 39 | Add to selection line o1 and press the key with the Latin character x, with the result that we will have the point symmetrical found. In total, we have four points through which must pass the outline of the sought quadric.
Рис. 38 |
|
| 40 | The fifth point can be found, for example, by intersection of horizontal lines drawn through the point p9 with a circumference d1, the point p9, press the key with the Latin character h, then add to the selection of the circle d1 and press the key with the Latin character p. Get the points p15 and p16, any of which can now be used to build an outline of the sought quadric.
Рис. 39 |
|
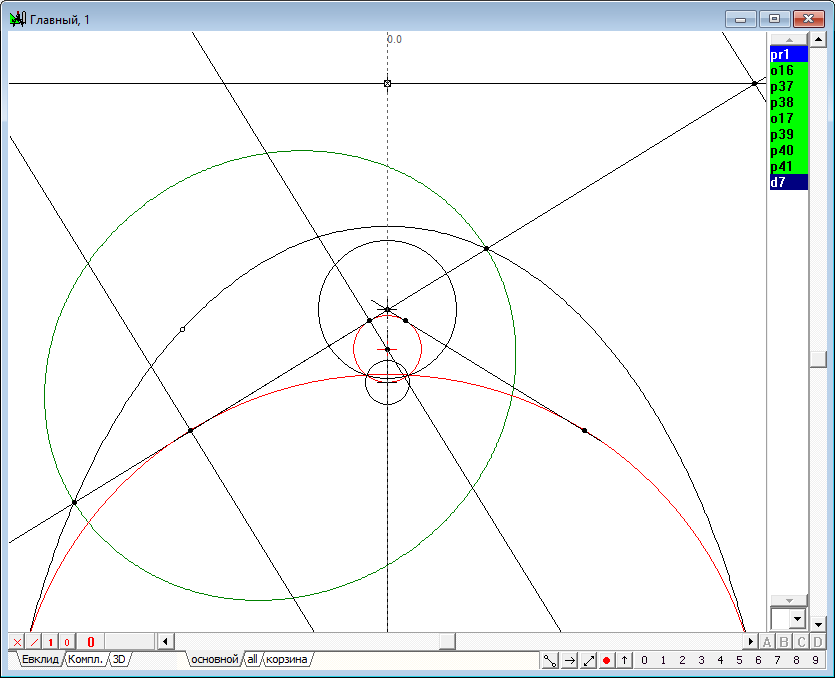
| 41 | Select points p12, p14, p11, p13 and p15 and press the key with the Latin character y, to build conic y1 - an outline of the desired quadric. It is clear that the quadric is controlled by a one-parameter set of points p7, taking different positions on the straight line o2. From the build shows that all quadric represent a bundle induced by two arbitrary spheres.
Рис. 40 |
|
| 42 | By pressing the symbol with the Latin f, we find the foci and directrix of a conic-outline.
Рис. 41 |
|
| 43 | Fix the position of the points, leaving only their selection by pressing on the key with the symbol =, which will lead to the formation of free points-copies of p19, p20 with coordinates equal to the current coordinates of points p17 and p18.
Рис. 42 |
|
| 44 | Repeat this step a couple more times, shifting the point p7 in such a way that the curve y1 has kept the form of hyperbole, the main real axis which coincides with the line connecting the centres of the original spheres.
Рис. 43 |
|
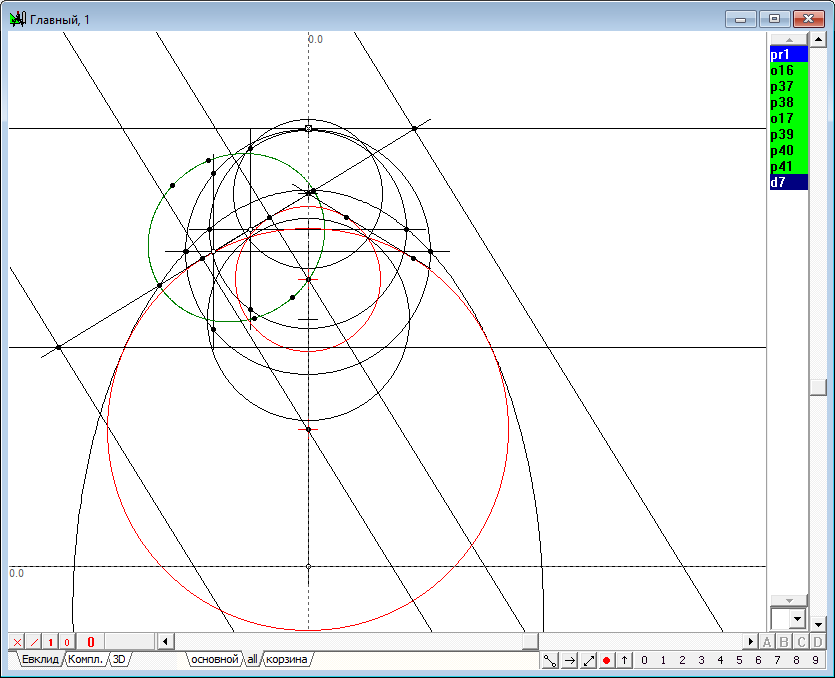
| 45 | Now select the points p19, p20 and p21 and press the key with the Latin character g, which will lead to the construction of a circle d3, which will take place not only through these points, but also through the rest just recorded copies of the focal points. In three-dimensional space, these points will correspond to the focal circumference of the quadric. Still family bundle of conics submitted by the hyperbole that passes tangent to two spheres in space forms a sphere, modeled in the drawing by the outline-circle d3. Pay attention to the fact that the diameter of this sphere is determined by the vertices of the cones, the simulated points of intersection of common tangents to the outlines of the original spheres. One such point - p27 can be constructed by intersection of lines o2 and o3. To plot the second point p32, it is necessary to highlight the circles d1 and d2 and click on the keys with the symbols o (lower case), 8 p.
Рис. 44 |
|
| 46 | Restoring the sphere of inversion for the source fields specified by the spheres outlines d1 and d2 (select them and press the key with the symbol R), we find that the sphere, built on many of the focal circles, and presented a outline d3 passes through the center of one of the spheres inversion point p32. This means that such a sphere is converted into the inversion will move in a plane that is modeled with radical axis of o17, built for the circles d1 and d2 (select them and press the key with the symbol r).
Рис. 45 |
|
| 47 | If the outlines of a quadric will take an elliptical shape or major axis of the hyperbola will be perpendicular to the line connecting the centers of the initial spheres, then their foci will be to move in a straight line o1. |
|
| 48 | Undo the build by pressing Ctrl+Z to the point where the conic outlines will represent a hyperbola with a major axis coincident with a line o1, and its foci are represented by points p17 and p18. Find the point of intersection of a straight line o1 of the circle d1 - p19 and p20, and then the point of intersection of a straight line o1 of the circle d2 of the points p21, p22. We define two involutions pr2 and pr3 in the following way:
Рис. 46 |
|
| 49 | Find dual points of projectivity pr2. Highlight its tag and press the key with the symbol p. Still selected, draw through the obtained point p24 and p25 circumference d3, by pressing the D key (upper case) and find its center p26, clicking on the button with the symbol c. We do the same with the second projectivities, which will build the real center p30 of the imaginary circle d4. Assigning the circle d5 with diameter points p26 and p30, we ascertain that the circumference is the geometric place of the points forming the foci of hyperbole, outlines, quadric. Let's denote the original sketches of the spheres in blue, and the essay "focal" areas in red.
Рис. 47 |
|
| 50 | Will gradually shift center p1 of the circle d1 with the help of shaper in the direction to the center of the circle d2. At some point, when the circles will intersect in real points, the total "internal" tangent circles will disappear. However, this will not lead to the fact that the outline of the quadric will not be built, as there are external tangents, they can be done and used to build the essay in the same way as in the case of using the internal tangents. This fact is confirmed by the actual presence of a circle d5, shown in red.
Рис. 48 |
|
| 51 | However, the greatest research interest is the case where the circle d1 is completely inside the circle d2. The presence of the red circle d5, gives grounds to conclude that the foci form a quadric continue to exist, which means that there are themselves of a quadric. However, the lack of a common tangent at the nested circles suggests that we are dealing with the manifestation of the properties of imaginary images in the problem of Dandelin. The study of this problem has not yet been completed. |