|
||
| Вернуться к перечню уроков | ||
| Представленная в данном уроке задача реализуется в среде программной системы Симплекс | ||
| 1 | Задача о сферах Данделена представляет собой одну из наиболее красивых и изящных геометрических конструкций, которую несложно реализовать при помощи относительно простых геометрических объектов в трехмерном пространстве. Условие задачи утверждает, что в произвольную квадрику и плоскость, ее пересекающую, можно вписать две сферы, названные в честь Данделена, причем эти сферы касаются плоскости в точках, являющихся фокусами коники - линии пересечения исходной квадрики и плоскости. Свойства сфер Данделена обычно рассматриваются на основе анализа метрических характеристик входящих в конструкцию объектов с применением аппарата аффинной геометрии. Однако, в действительности, истинная природа этой задачи сугубо проективная, и она мало изучена. Геометрическая конструкция задачи о сферах Данделена имеет много общего с задачами Аполлония и Ферма, рассмотренных в предыдущих примерах серии уроков по использованию системы Симплекс для решения задач конструктивной геометрии. В данном уроке нам предстоит познакомиться с тем, каким образом реализовать геометрическую конструкцию построения сфер Данделена, и исследовать возникающие в этой задаче проективные свойства. Это исследование позволит нам обнаружить геометрическое родство, объединяющее объекты этой конструкции и, следовательно, понять эту конструкцию не только с точки зрения ее реализации в действительном пространстве, но и в пространстве мнимых образов, а также внести в повестку дня вопрос о поиске подобных конструкций в пространствах более высоких размерностей. |
|
| 2 | Приступим к построению сфер Данделена. Зададим исходные данные - произвольную Квадрику и секущую плоскость. Без потери общности реализуем это построение на примере эллипсоида, задав его репер осью вращения и образующей - эллипса, который, впрочем, мы сможем без труда трансформировать в любую конику. | |
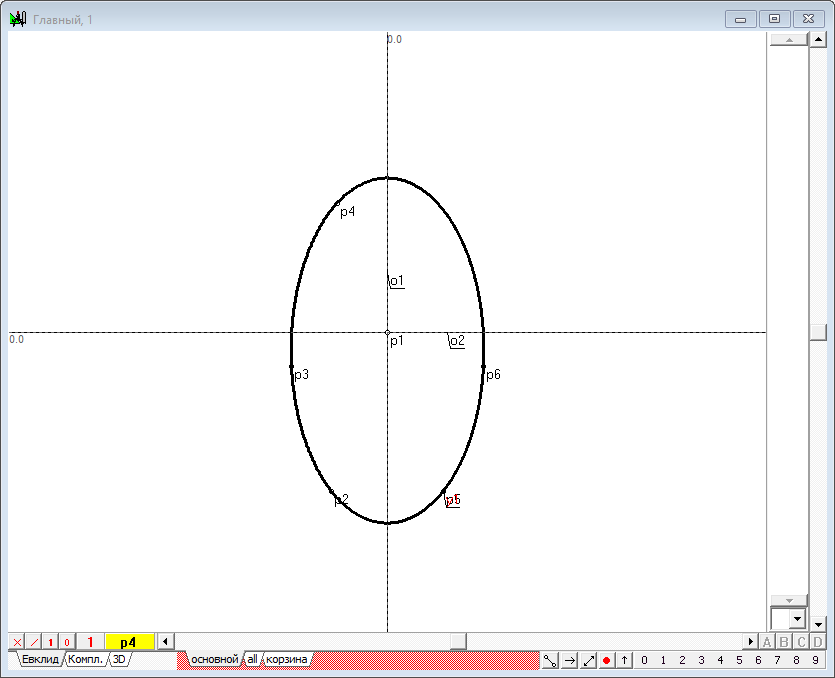
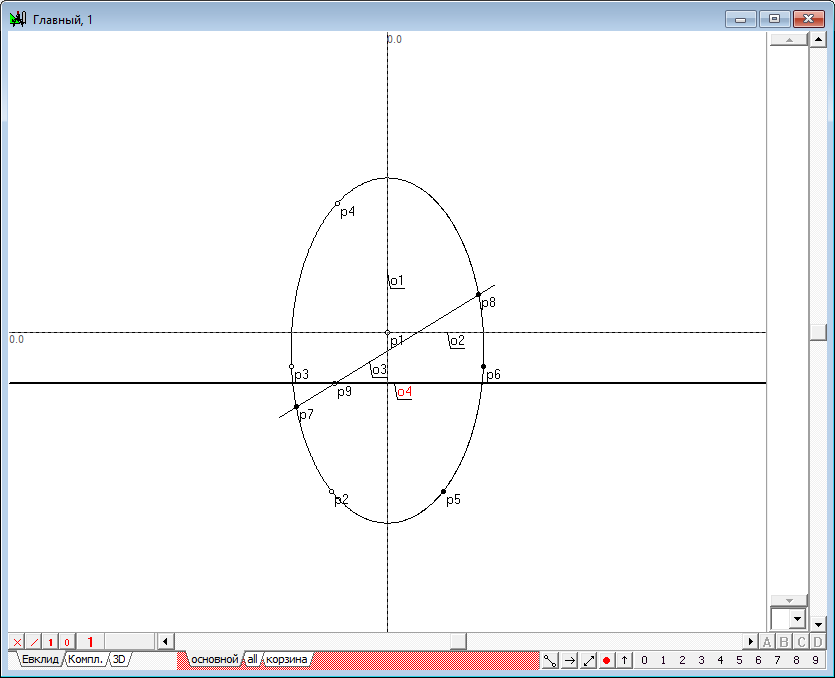
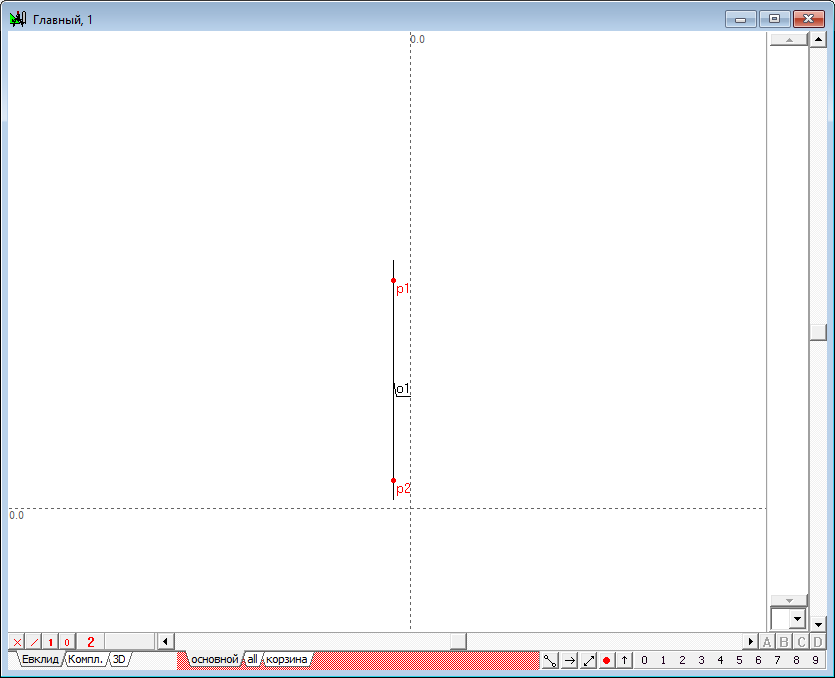
| 3 | Проведем две оси, одну из которых будем считать осью квадрики. Для этого нажмем на клавиатуре клавишу с латинским символом z. Ось o1 будем использовать в качестве оси квадрики.
Рис. 1 |
|
| 4 | Используя инструмент Свободная точка, разместим на плоскости три точки p2, p3 и p4.
Рис. 2 |
|
| 5 | Выделим две точки (например, p2 и p3) и ось o1.
Рис. 3 |
|
| 6 | Нажав на клавиатуре клавишу с латинским символом x, построим точки p5 и p6, симметричные точками p2 и p3 относительно прямой линии o1.
Рис. 4 |
|
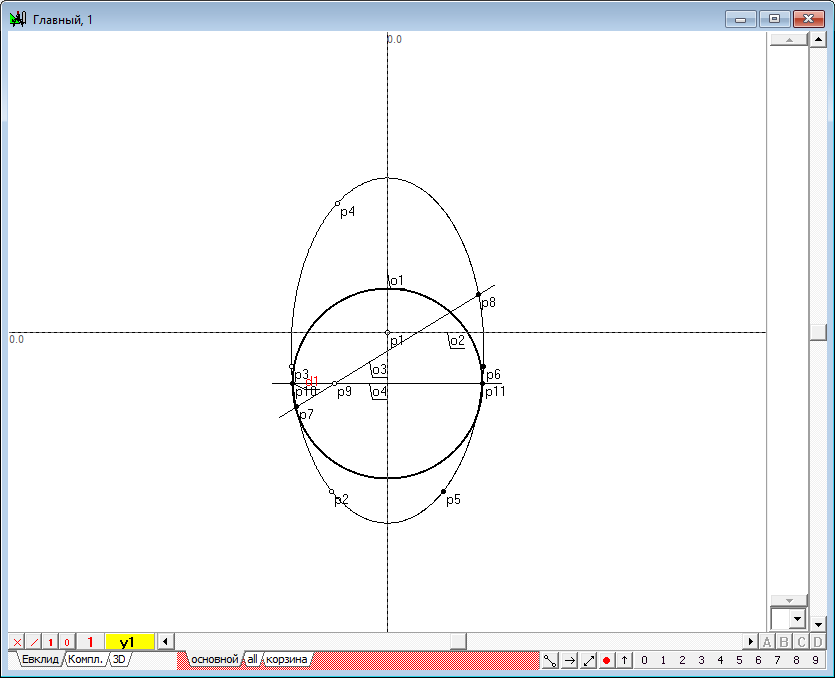
| 7 | Удерживая нажатой клавишу Shift, добавим к уже имеющемуся выделению точки p2, p3, и p4 и, нажав на клавиатуре клавишу с латинским символом y, построим конику y1.
Рис. 5 |
|
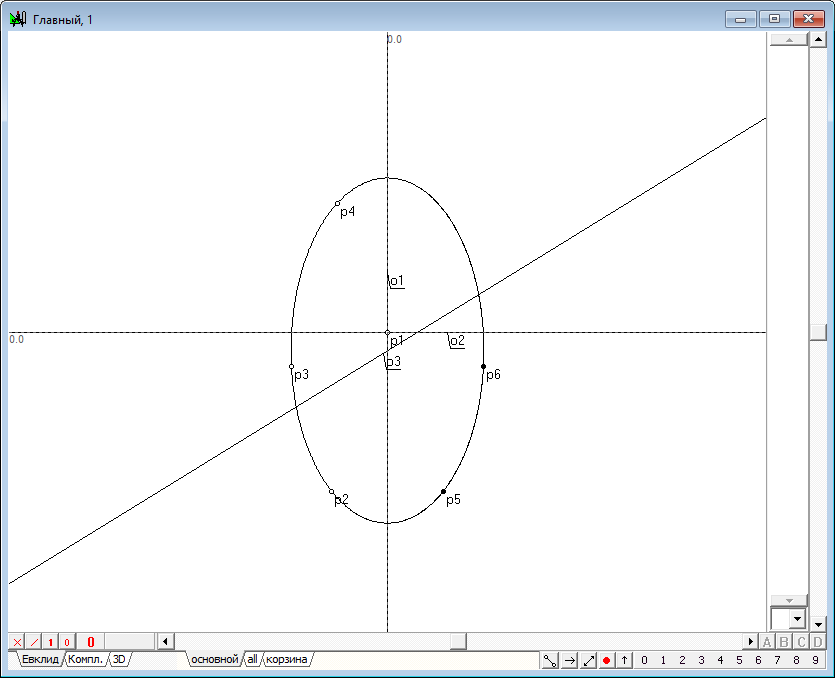
| 8 | Воспользовавшись инструментом Свободная прямая, проведем под некоторым произвольным углом линию o3, так чтобы на чертеже она явно пересекала эллипс y1. Эта линия будет использована как модель плоскости, занимающей проецирующее положение и секущей квадрику, заданную осью и коникой, с целью получения линии сечения.
Рис. 6 |
|
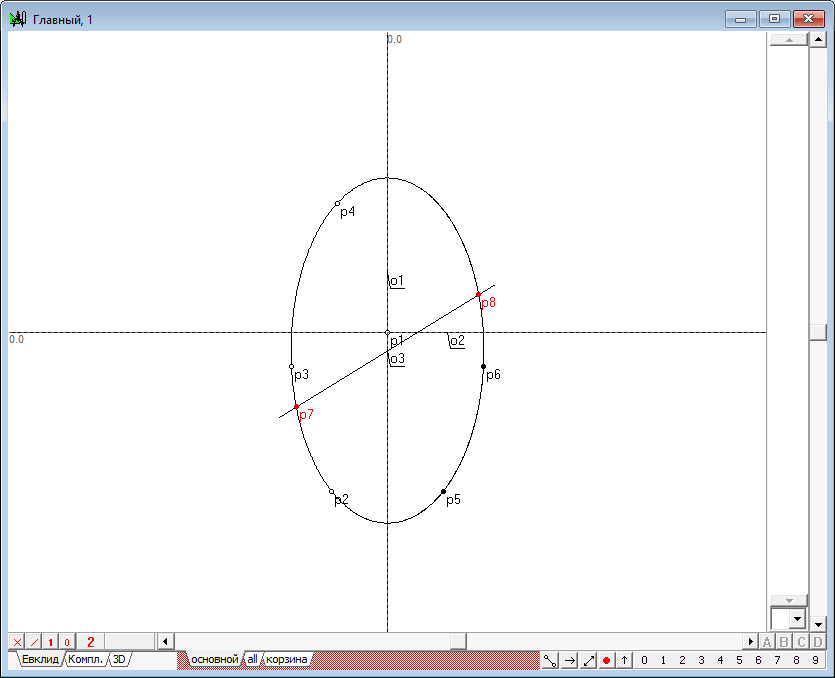
| 9 | Известно, что такой линией должна быть коника, поэтому для ее определения нам потребуется найти по крайней мере пять точек, принадлежащих этой конике. Для этого мы решим задачу о нахождении таких точек на поверхности квадрики. Две точки из необходимых пяти найти достаточно легко. Для этого необходимо найти точки пересечения линии o3 и коники y1. Для их получения выделим объекты o3 и y1 и, нажав на клавиатуре клавишу с латинским символом p, получим точки p7 и p8.
Рис. 7 |
|
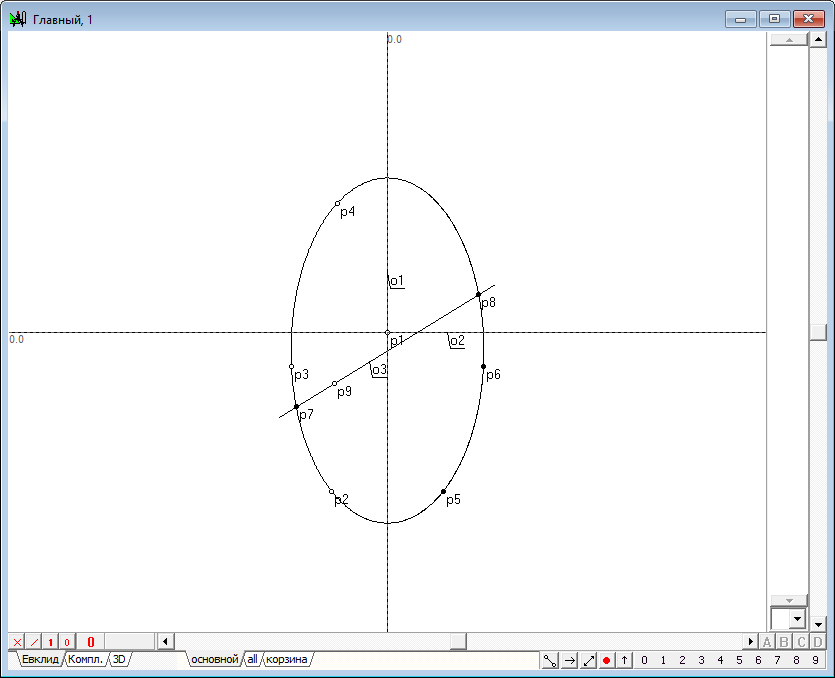
| 10 | Для получения остальных точек дважды воспользуемся тем обстоятельством, что плоскость, перпендикулярная оси квадрики, пересекает квадрику по окружности. Вначале снимем выделение с объектов. Затем, удерживая нажатой клавишу Ctrl, подведем курсор в такое положение, чтобы он разместился где-нибудь над изображением прямой линии o3 и щелкнем левой кнопкой мышки. Это действие позволит задать на прямой o3 точку p9. Эту точку мы будем использовать для позиционирования дополнительной секущей плоскости, которую мы проведем перпендикулярно к оси квадрики.
Рис. 8 |
|
| 11 | Выделим точку p9 и, нажав на клавиатуре клавишу с латинским символом h, проведем горизонтальную линию o4, моделирующую такую плоскость.
Рис. 9 |
|
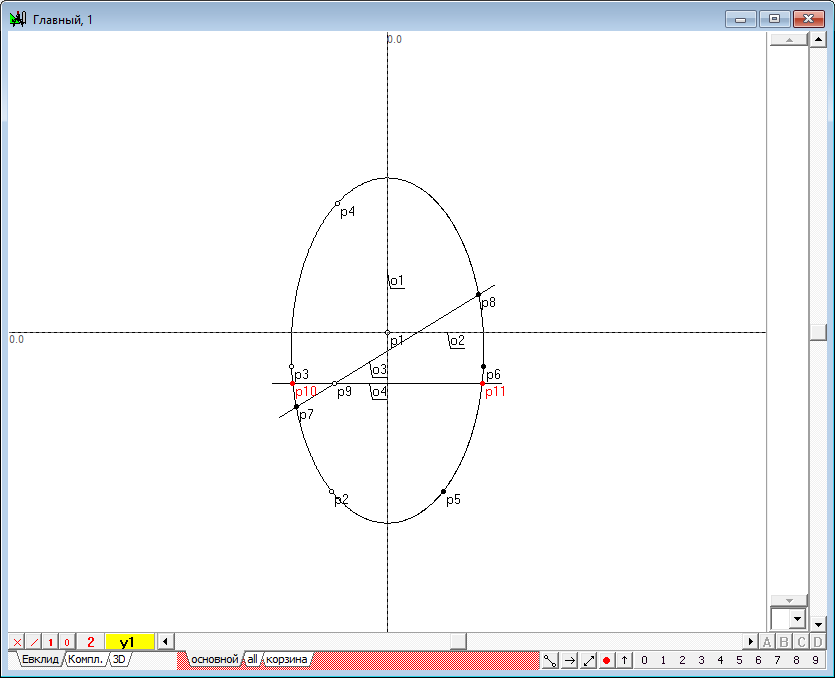
| 12 | Удерживая нажатой клавишу Shift, добавим к выделению конику y1 и нажмем на клавиатуре клавишу с латинским символом p. В результате получим точки p10 и p11, которые позволяют определить диаметр окружности - результата сечения дополнительной плоскостью исходной квадрики.
Рис. 10 |
|
| 13 | Точки p10 и p11 задают отрезок - фронтальное изображение этой окружности. Для получения горизонтального вида (окружности d1, изображенной в натуральную величину), нажмем на клавиатуре клавишу с латинским символом D (верхний регистр).
Рис. 11 |
|
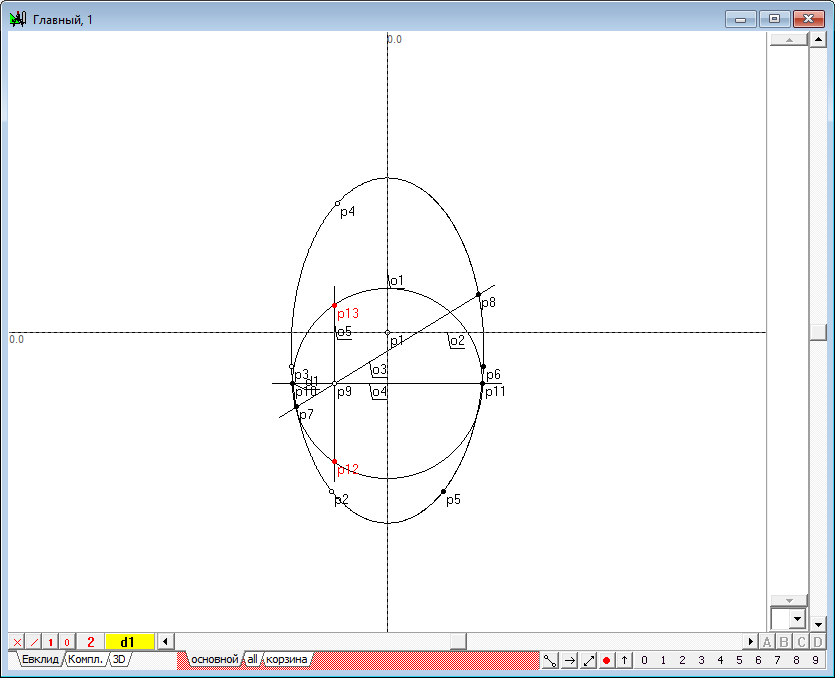
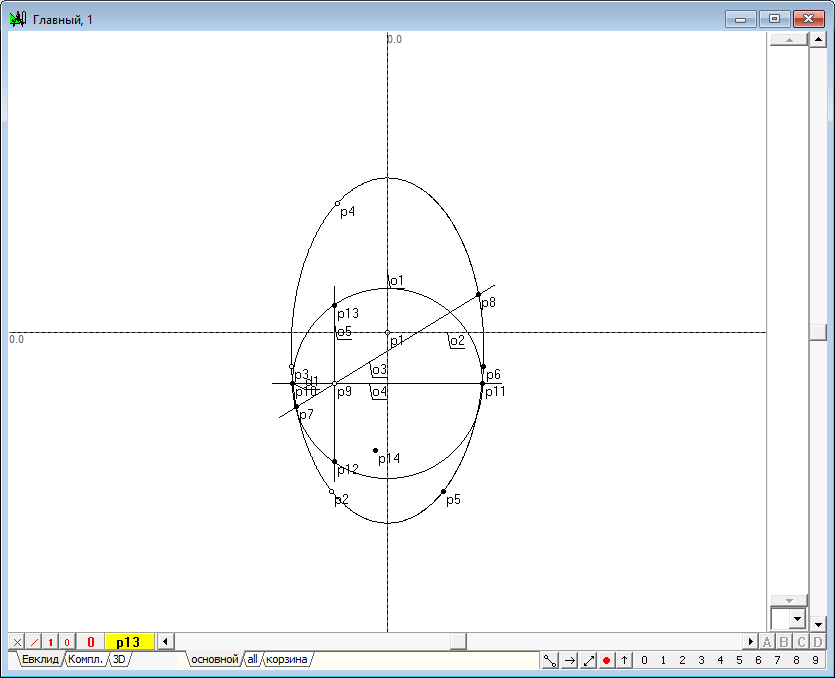
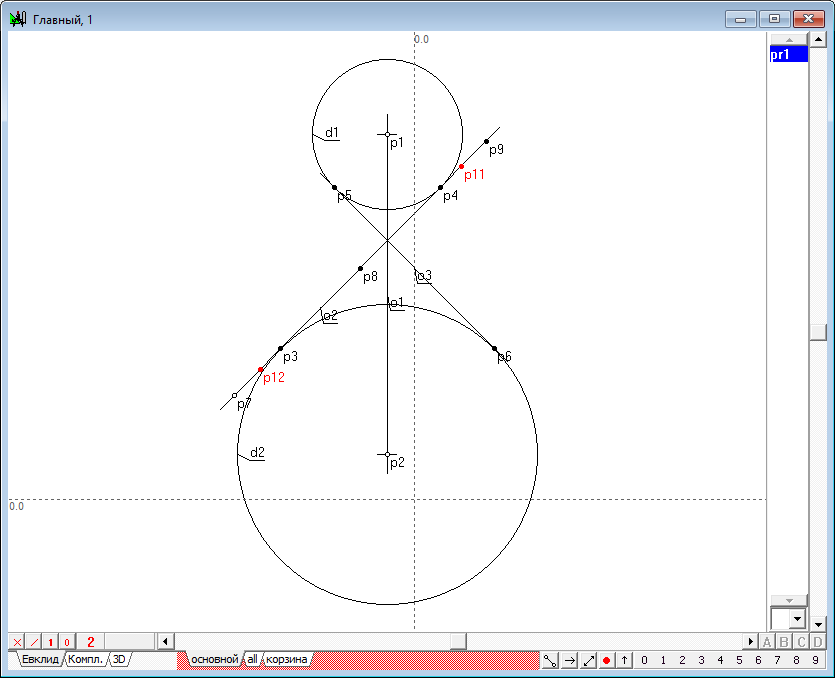
| 14 | Построим две точки, которые будут общими как для окружности, так и для искомой коники в рассматриваемой дополнительной ортогональной плоскости. Фронтальные проекции этих точек известны - они моделируются точкой p9. Горизонтальные проекции нетрудно найти, если через точку p9 провести вертикальную прямую и найти точки ее пересечения с окружностью d1. Для выполнения этого построения выделим точку p9 и нажмем на клавиатуре клавишу с латинским символом v. Затем, удерживая нажатой клавишу Shift, добавим к выделению окружность d1 и, нажав на клавиатуре клавишу с латинским символом p, получим искомые точки p12 и p13.
Рис. 12 |
|
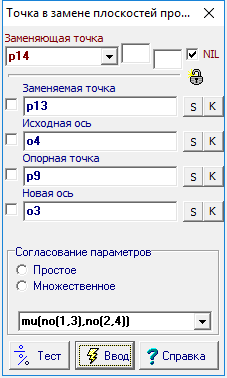
| 15 | Теперь наша задача заключается в том, чтобы по имеющимся данным мы бы построили изображение линии сечения исходной плоскости с квадрикой. Фронтальное и при этом вырожденное в отрезок изображение этой линии нам известно - это отрезок между точками p7 и p8. Поэтому нам следует восстановить дополнительную ортогональную проекцию этой линии, приняв за новую ось преобразования линию o3, а опираться при переходе в новую систему проекций из "старой" будем, используя прямую линию o4. Вызовем функцию Точка в замене плоскостей проекций и заполним поля диалогового окна, определяющего входные параметры этой функции так, как это указано на рисунке 13.
Рис. 13 |
|
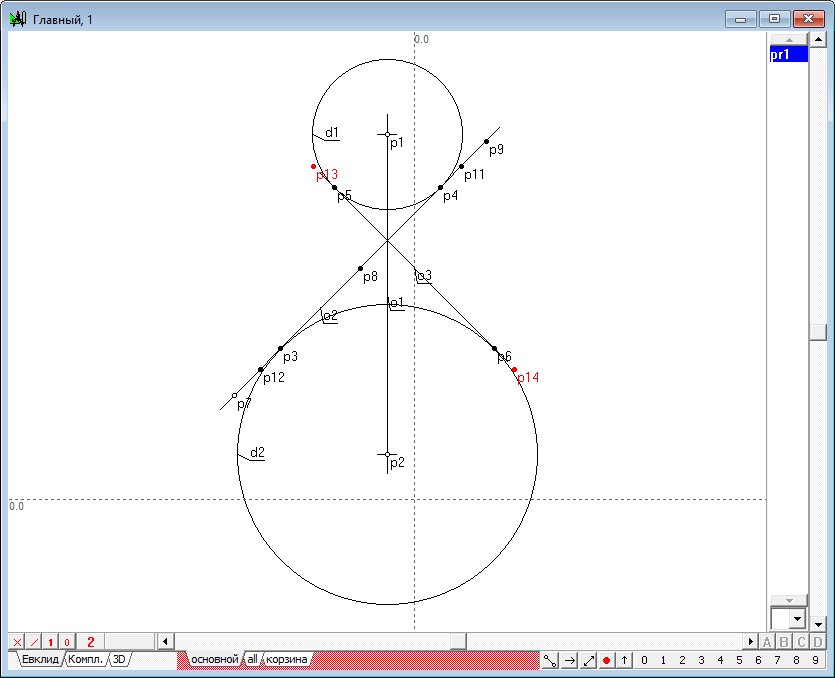
| 16 | После нажатия н кнопку Ввод, мы получим точку p14 - одну из тех точек, которую нам необходимо определить для построения истинной величины искомого конического сечения.
Рис. 14 |
|
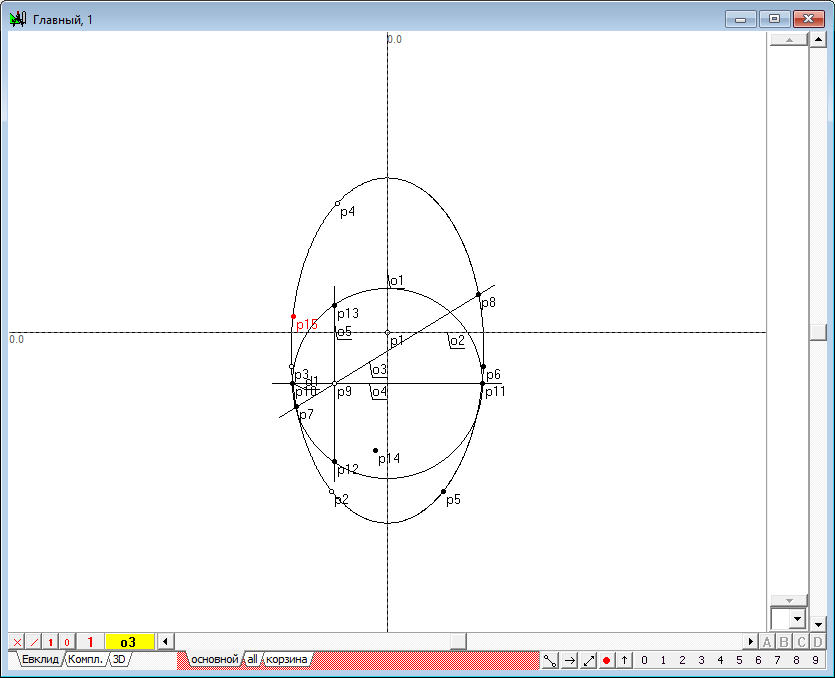
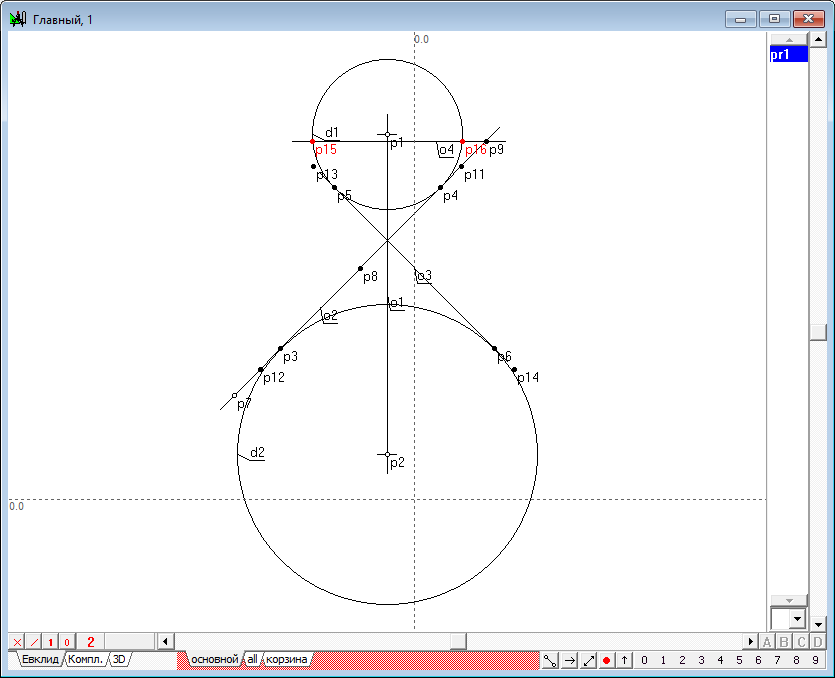
| 17 | Не составит труда построить и точку p15, симметричную p14 в отношении оси o3. Для этого, выделив последовательно точку p14 и прямую линию o3, нажмем на клавиатуре клавишу с латинским символом x.
Рис. 15 |
|
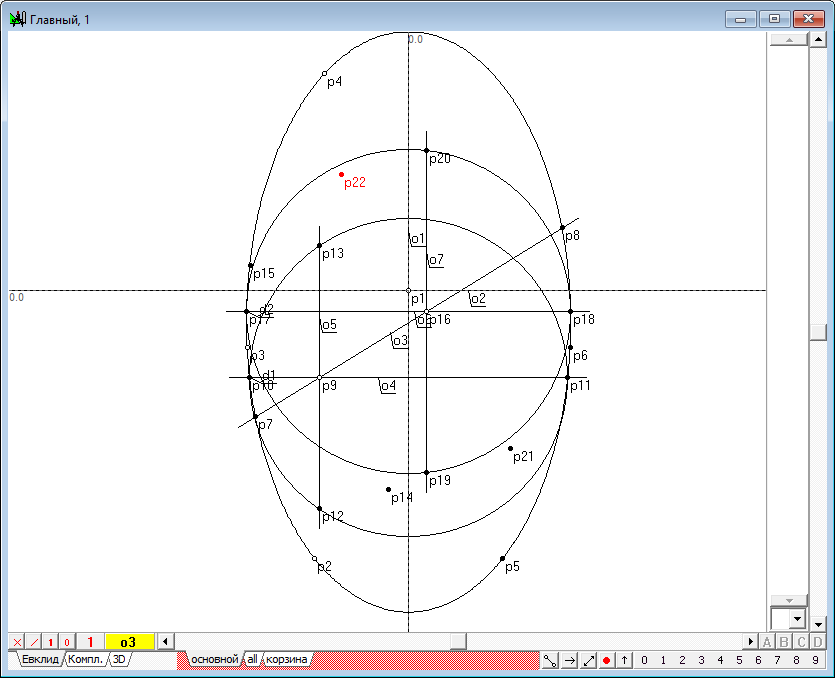
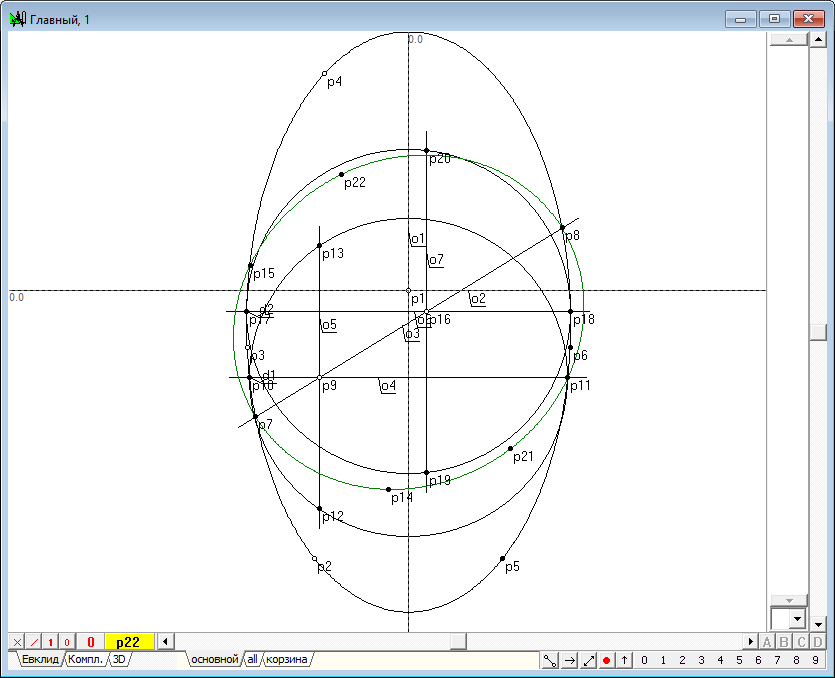
| 18 | Итак, нам известны четыре точки будущей коники. Поскольку коника однозначно строится по пяти точкам, не хватает еще одной точки. Поэтому, разместив аналогично точке p9 на прямой еще одну точку p16, повторим только что выполненные построения еще один раз. В результате, получим точки p21 и p22, одна из которых избыточна и может быть использована для визуальной проверки того факта, что все построенные точки действительно лежат на искомой конике.
Рис. 16 |
|
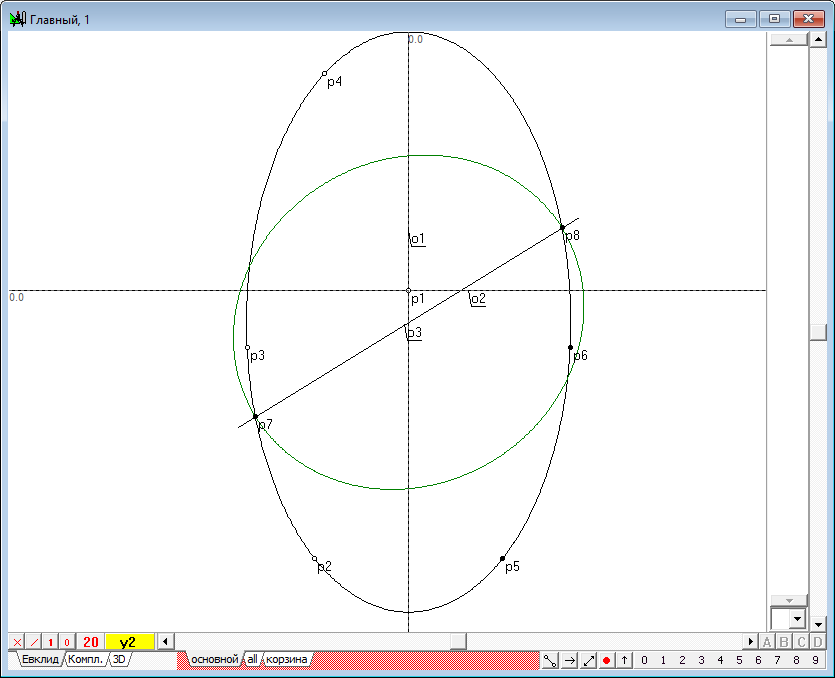
| 19 | Проведем искомую конику y2. Для этого выделим точки p21, p8, p14, p15 и p7 и нажмем на клавиатуре клавишу с латинским символом y.
Рис. 17 |
|
| 20 | Поскольку выполненные нами построения имели вспомогательный характер и для последующего решения задачи интереса не представляют, то имеет смысл изображения вспомогательных объектов перенести в слой корзина. Для этого выделим все те объекты, которые нам более не нужны, и нажмем на клавиатуре клавишу с символом \. Такое выделение легко выполнить, если вначале выделить только точки p9 и p16, затем, вызвав правой кнопкой мышки контекстное меню выбрать режим выделения С потомками. В результате выделятся все те объекты, которые непосредственно зависят от точек p9 и p16. Однако среди этих объектов окажется и искомая коника. Она нам будет еще нужна. Для того чтобы исключить конику y2 из выделения, нажмем на клавишу Shift, переместим курсор так, чтобы он расположился над изображением коники y2, и щелкнем левой кнопкой мышки. Выделение с коники будет снято, в то время как все остальные объекты, подлежащие переносу в слой корзина, в выделении сохранятся.
Рис. 18 |
|
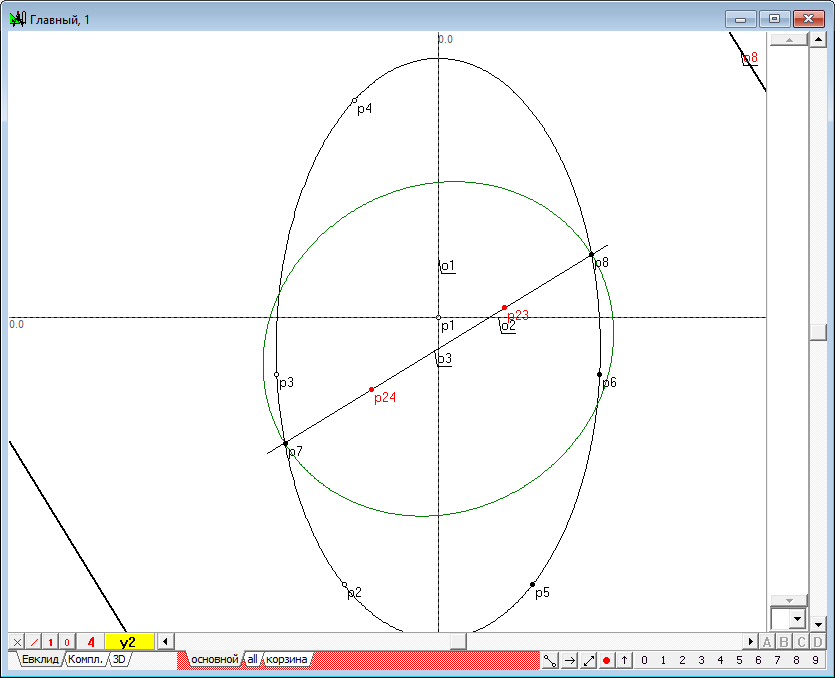
| 21 | Итак, коника построена. Найдем ее фокусы и директрисы. Для этого выделим конику и нажмем на клавиатуре клавишу с латинским символом f.
Рис. 19 |
|
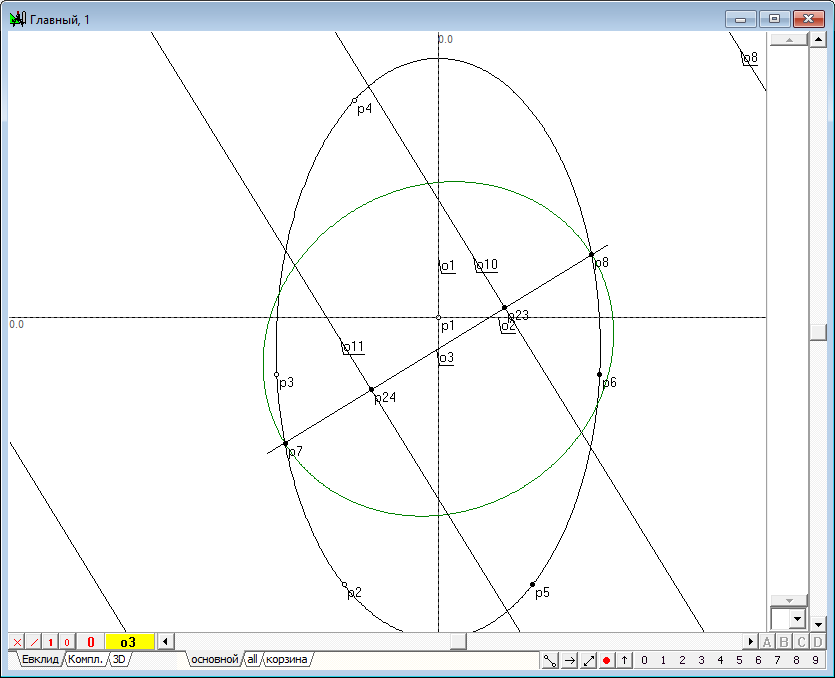
| 22 | Понятно, что центы сфер Данделена должны лежать на оси исходной квадрики. Восстановим из точек p23 и p24 перпендикуляры к линии o3. Для этого выделим сначала точку p23 и прямую линию o3 и нажмем на клавиатуре клавишу с латинским символом o. Получим линию o10. Затем аналогичные действия повторим в отношении точки p24 и получим линию o11.
Рис. 20 |
|
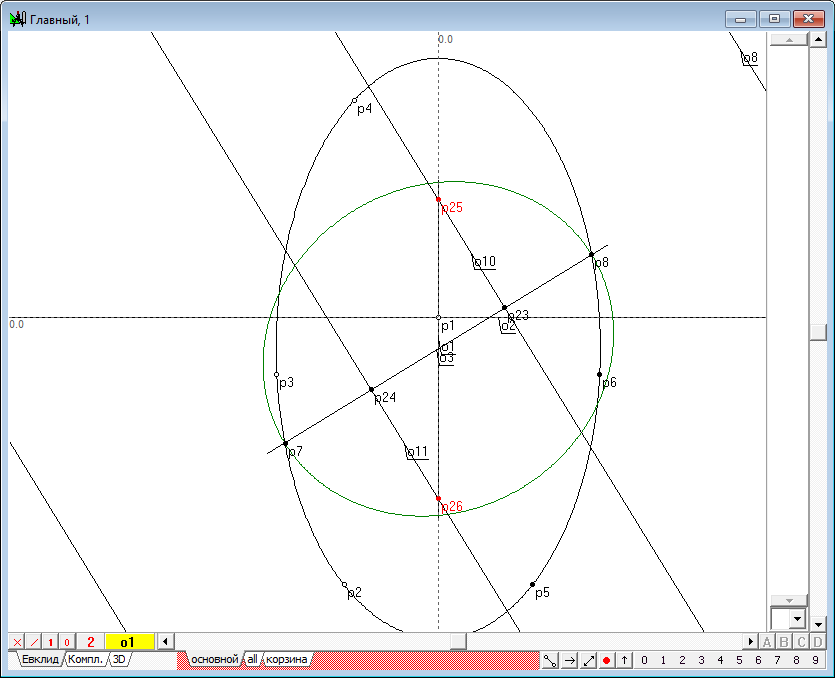
| 23 | Выделим последовательно линии o10, o11 и o1 и нажмем на клавиатуре клавишу с латинским символом p. Мы получим центры сфер Данделена - точки p25 и p26.
Рис. 21 |
|
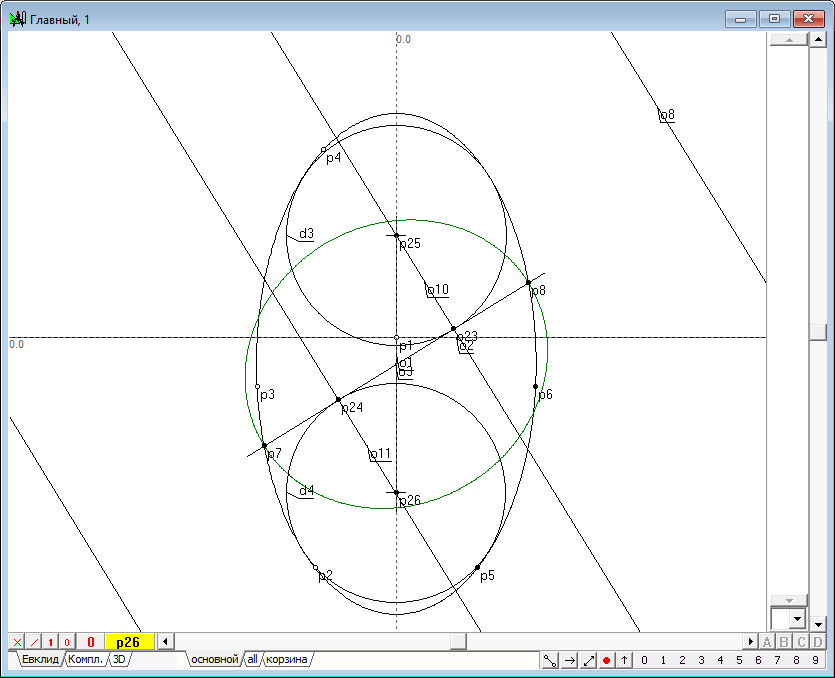
| 24 | Сейчас можно построить и очерки самих сфер. Выделим последовательно точки p23 и p25 и нажмем на клавиатуре клавишу с латинским символом d. Получим окружность d3. Выделим последовательно точки p24 и p26 и нажмем на клавиатуре клавишу с латинским символом d. Получим окружность d4. Окружности d3 и d4 - очерковые образующие сфер Данделена во фронтальной проекции. Мы действительно наблюдаем касание этих сфер к образующей исходной квадрики и к исходной плоскости.
Рис. 22 |
|
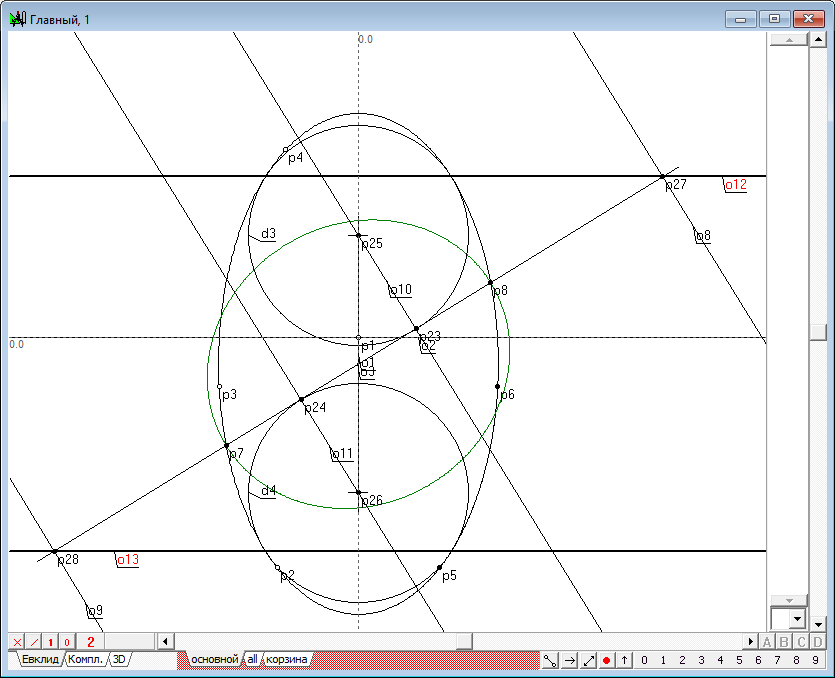
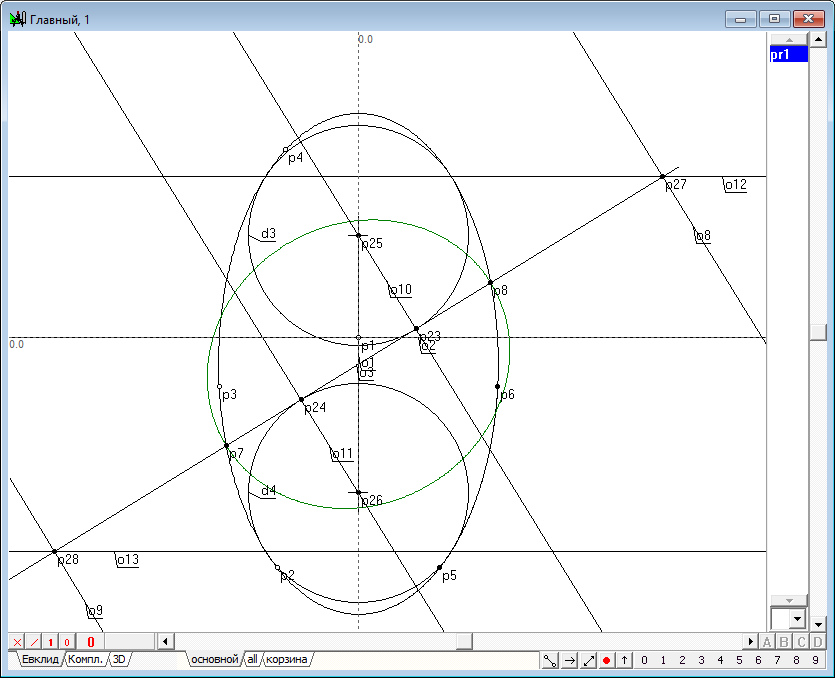
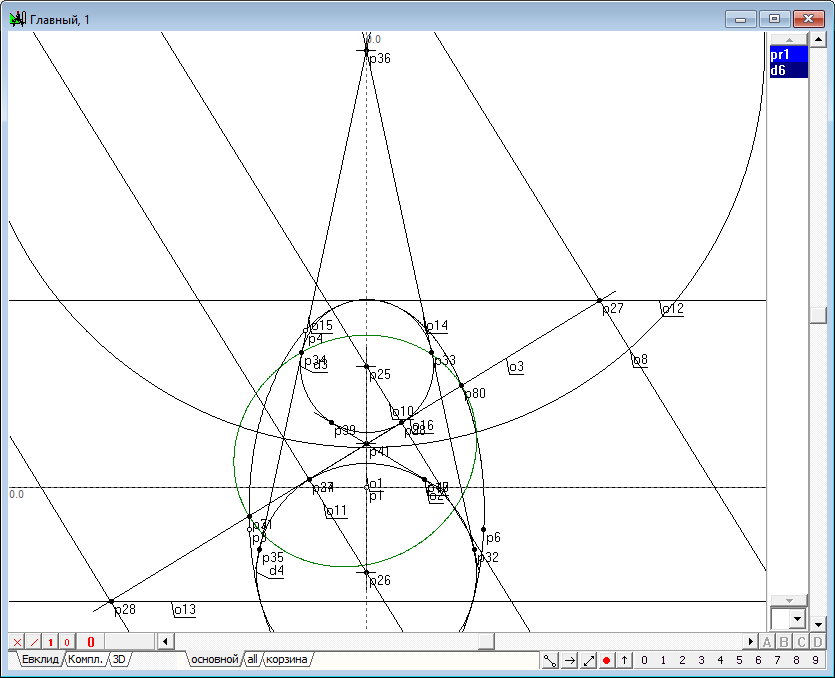
| 25 | Сферы Данделена построены. Теперь приступим к изучению проективных свойств полученной конструкции. Найдем точки пересечения директрис o8 и o9 коники y2 с прямой линией o3.Для этого выделим эти линии последовательно и нажмем на клавиатуре на клавишу с латинским символом p. Получим точки p27 и p28. Затем, не снимая выделения, нажмем на клавиатуре клавишу с латинским символом h, что позволит нам получить две горизонтальные линии o12 и o13. Заметим, что эти линии пересекают очерки сфер Данделена и исходной коники в точках касания, а в трехмерном пространстве этими линиями задаются окружности касания сфер Данделена и исходной квадрики.
Рис. 23 |
|
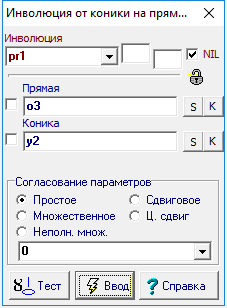
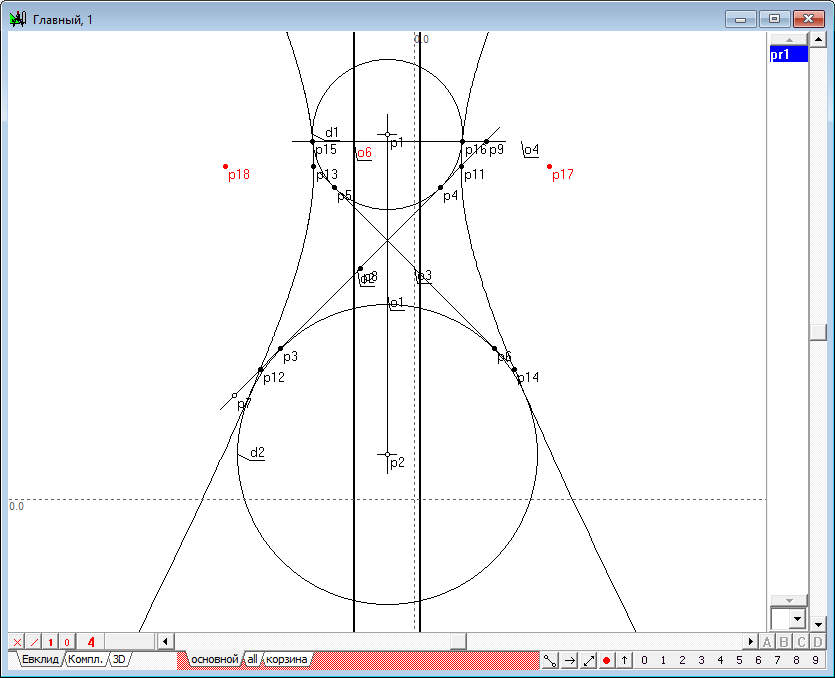
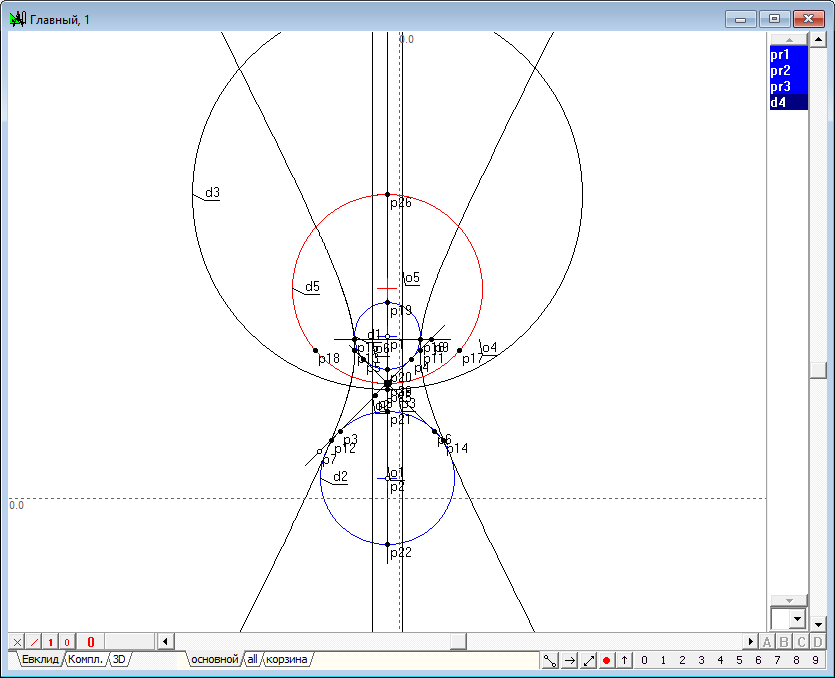
| 26 | Известно, что коника индуцирует на прямой линии инволюцию. Зададим такую инволюцию, вызвав функцию Инволюция от коники на прямой.
Рис. 24
Рис. 25 |
|
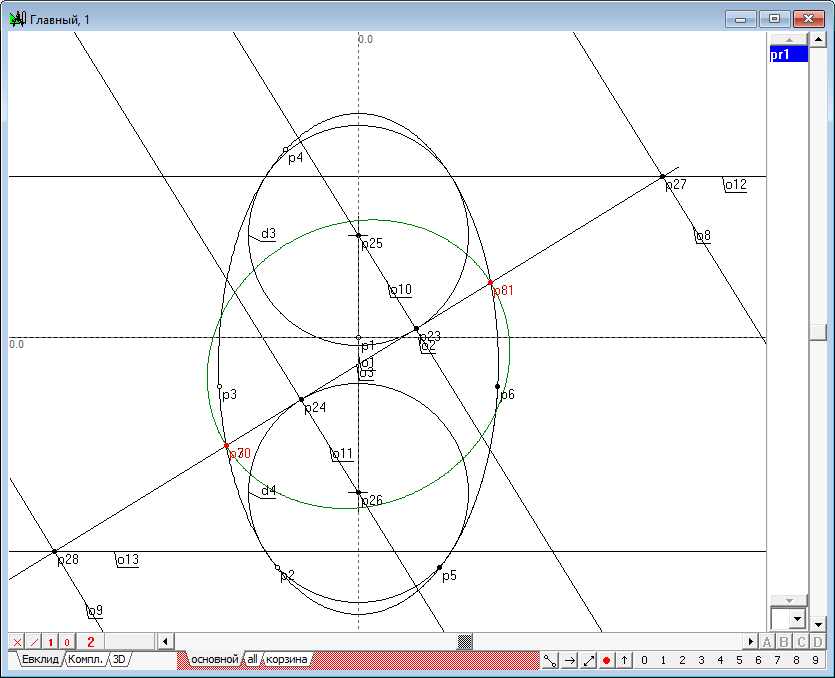
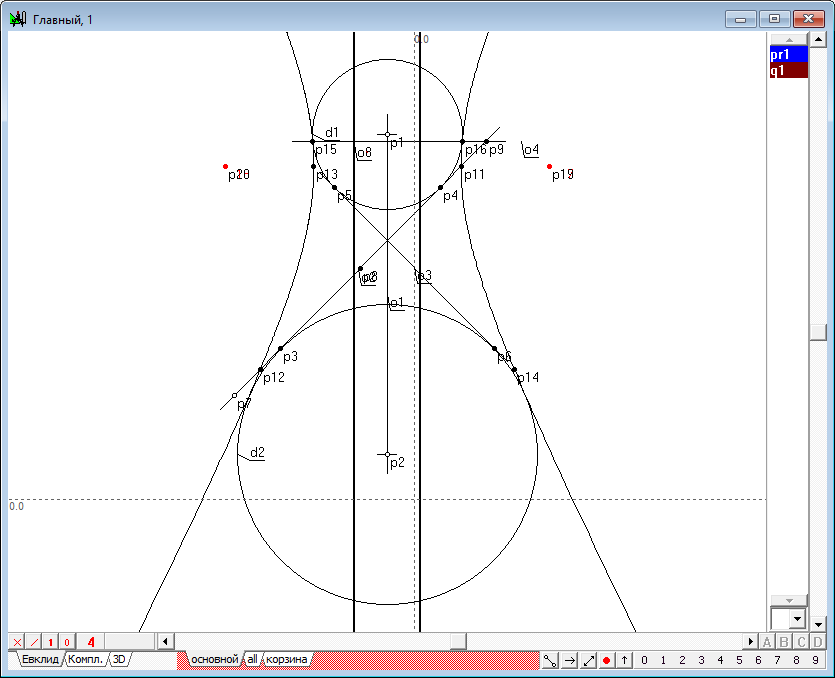
| 27 | Известно также, что двойными точками этой инволюции являются точки пересечения этой прямой с коникой, причем под точками пересечения понимаются как действительные точки, так и мнимые. Проверим это. Выделим метку инволюции pr1 и нажмем на клавиатуре клавишу с латинским символом p. Получим две точки, совпадающие с точками p7 и p8.
Рис. 26 |
|
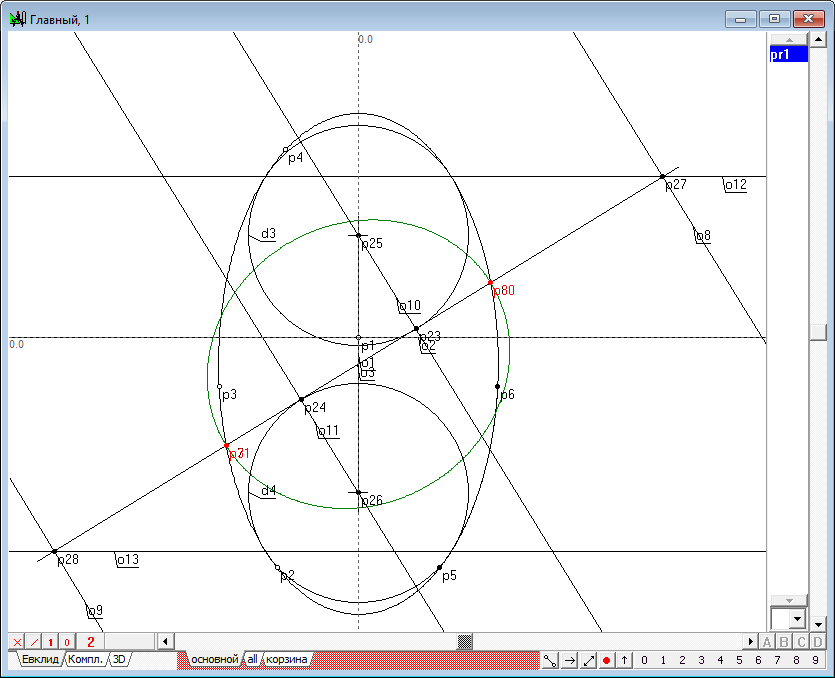
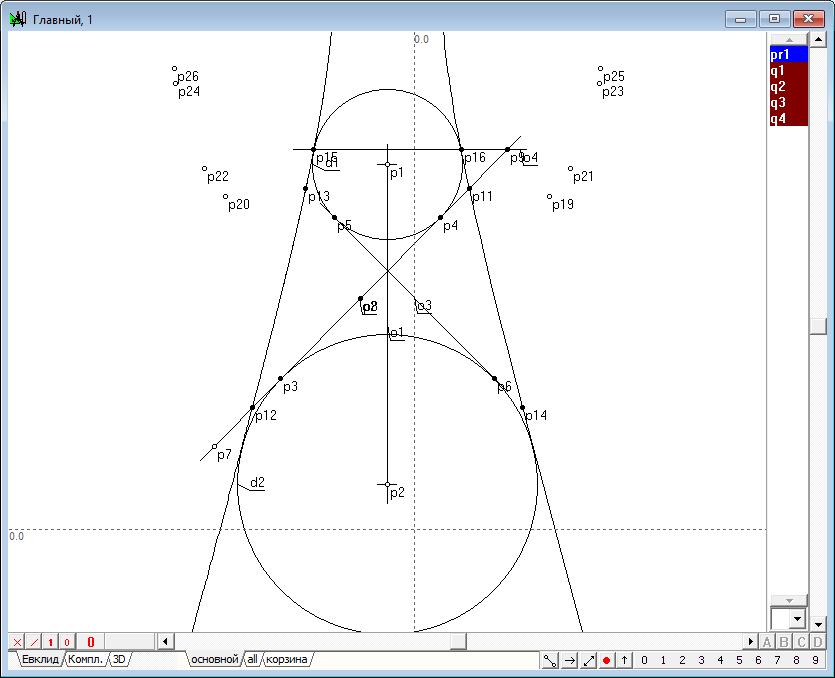
| 28 | Отменим два последних действия, дважды нажав на комбинацию клавиш Ctrl+Z. Теперь зададим инволюцию по-другому. Удерживая нажатой клавишу Shift, выделим последовательно точки p28, p24, p23 и p27, а затем добавим к выделению прямую o3, после чего нажмем на клавиатуре клавишу с латинским символом k. После определения инволюции pr1 нажмем на клавиатуре клавишу с латинским символом p, чтобы получить двойные точки этой инволюции. Нетрудно убедиться в том, что и в этом случае двойные точки инволюции совпадают с точками пересечения прямой o3 и коники y2.
Рис. 27 |
|
| 29 | Построим сферы инверсии для найденных сфер Данделена. Поскольку в нашем примере сферы Данделена не пересекаются, то одна из сфер инверсии будет действительной, а вторая - мнимой. Выделим окружности d3 и d4 и нажмем на клавиатуре клавишу с латинским символом R (верхний регистр). Получим окружности d5 и d6.
Рис. 28 |
|
| 30 | Центры двух сфер инверсии находятся в вершинах двух конусов, касательных к сферам Данделена. Для проверки этого факта построим общие касательные к очерковым окружностям сфер Данделена. Выделим окружности d3 и d4 и нажмем на клавиатуре последовательно на клавиши o, 8, p. Затем снова выделим эти окружности и нажмем на клавиатуре последовательно на клавиши O (верхний регистр), 8, p. Получим очерки двух конусов, описанных около двух сфер. Вершины конусов p36 и p41 совпадают с центрами инверсных сфер - одной действительной и одной мнимой.
Рис. 29 |
|
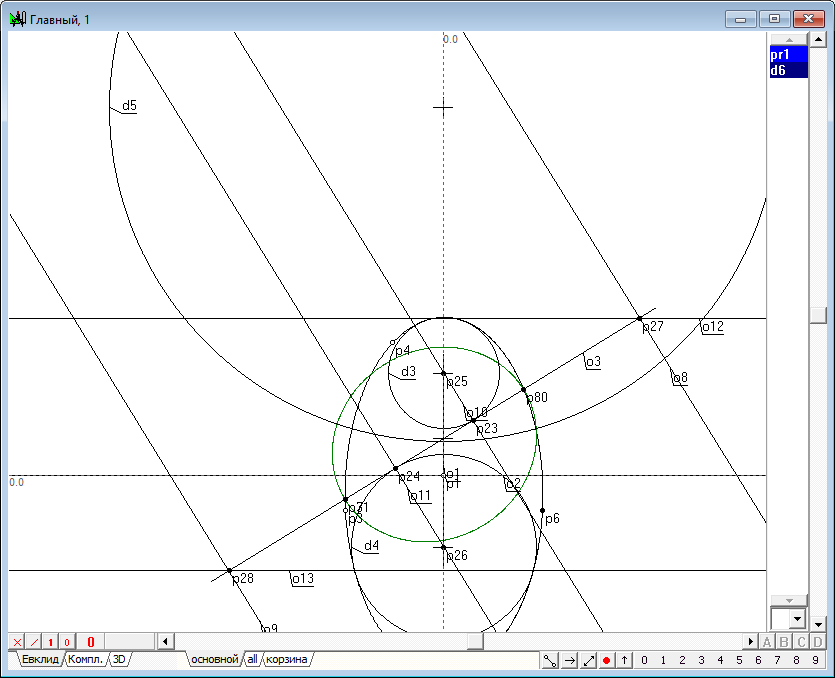
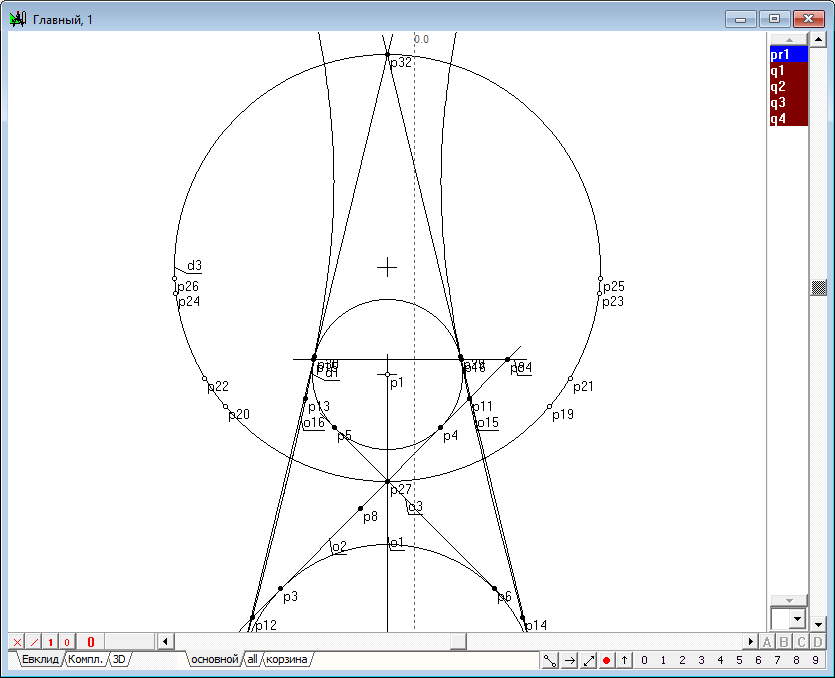
| 31 | Хотелось бы подчеркнуть особо, что в данном построении мы обнаружили проявление проективных свойств в геометрической конструкции задачи Данделена. Исследуем их проявления более подробно. Переместим с помощью шейпера прямую o3 вверх, параллельно ее прежнему положению, и зафиксируем ее в таком положении, при котором прямая o12 перестанет образовывать действительные точки пересечения с образующей квадрики - коникой y1.
Рис. 30 |
|
| 32 | Мы обнаружим при этом, что очерк сферы - окружность d3 - будет действительным, однако явного касания с очерком квадрики на чертеже не прослеживается. Тем не менее, в силу общности построений можно утверждать, что сфера, моделируемая фронтальным очерком - окружностью d3 - существует и она так же является сферой Данделена. Эта сфера имеет мнимое касание с исходной квадрикой. И сфера, и квадрика являются элементами пучка квадрик, определяемой мнимой окружностью, задающей этот пучок. Диаметральные точки этой окружности можно легко найти, если построить мнимые точки пересечения окружности d3 и прямой o12, а также мнимые точки пересечения коники y1 и прямой o12. Несложно также убедиться в том, что координаты этих точек соответствуют друг другу. Эти построения рекомендуется выполнить самостоятельно и убедиться в том, что они дают одинаковые результаты. | |
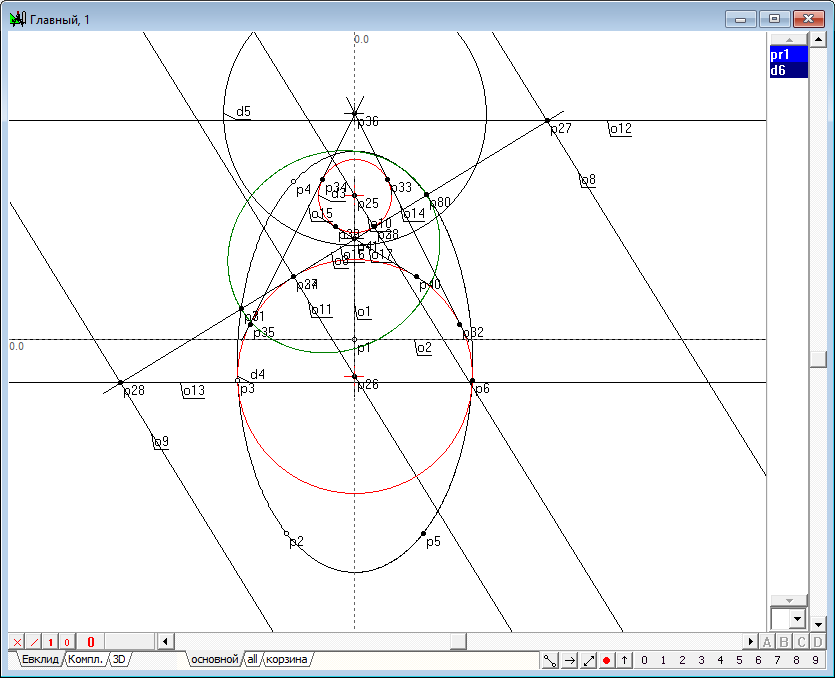
| 33 | Как видно из построения, представленного на рисунке, действительная сфера Данделена существует даже в том случае, когда плоскость поднялась "выше" ее центра.
Рис. 31
Рис. 32 |
|
| 34 | Теперь решим задачу, противоположную в своей формулировке к только что рассмотренной. Пусть даны две произвольные сферы. Построить квадрику, для которой данные сферы являются сферами Данделена. Покажем, что квадрики, удовлетворяющие данному условию, образуют однопараметрический пучок и исследуем некоторые свойства объектов этого пучка. Зададим две произвольные сферы. Построим прямую линию, несущую на себе две точки, нажав на клавиатуре клавишу с латинским символом V (верхний регистр).
Рис. 33 |
|
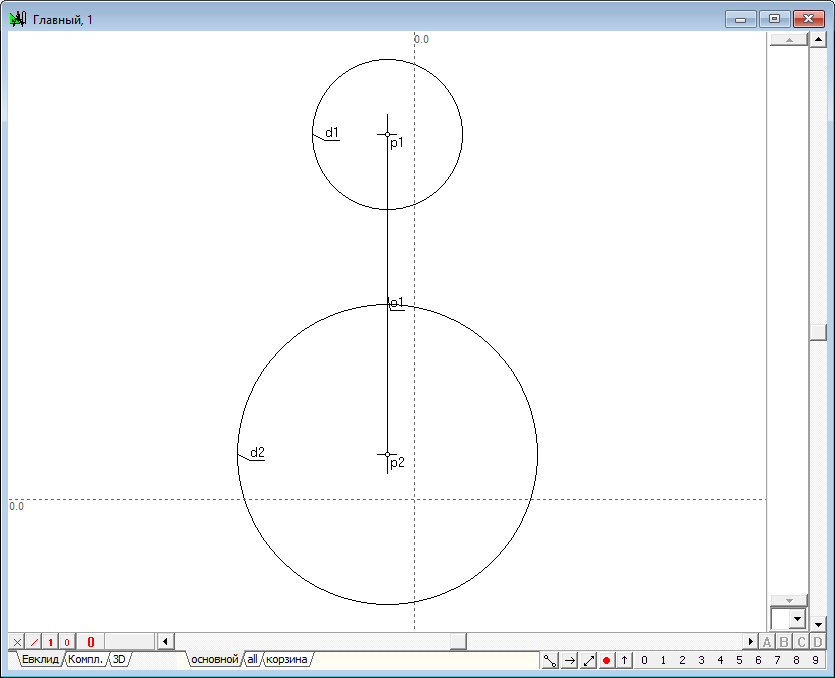
| 35 | Оставим в выделении только точку p1 и нажмем на клавиатуре клавишу с латинским символом d. Получим окружность d1 с центром в p1 и радиусом, определяемым текущем положением курсора. Построим аналогично окружность d2 с центром в точке p2.
Рис. 34 |
|
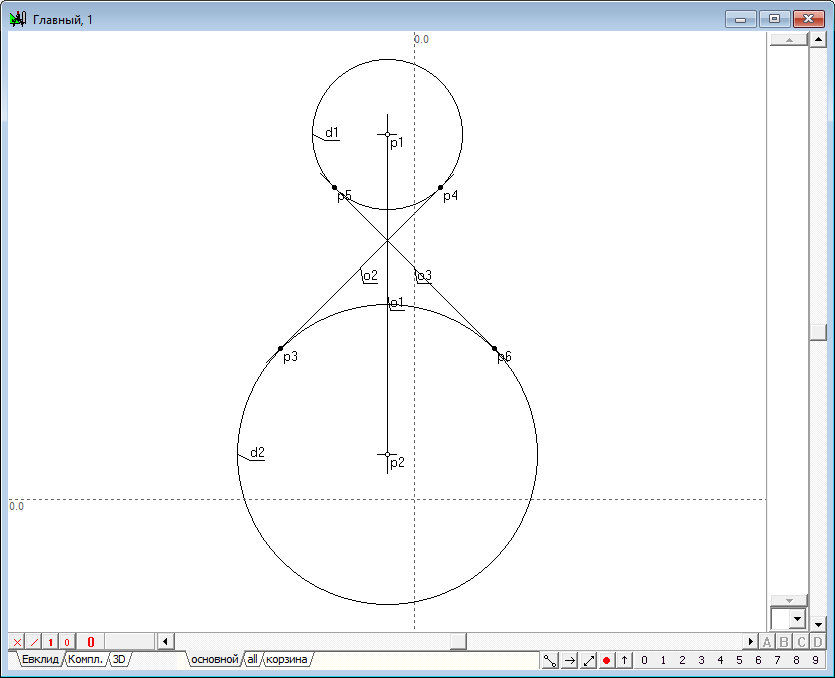
| 36 | Проведем линии, касательные к окружностям d1 и d2. Для этого выделим окружности и нажмем на клавиатуре клавишу с латинским символом O (верхний регистр).
Рис. 35 |
|
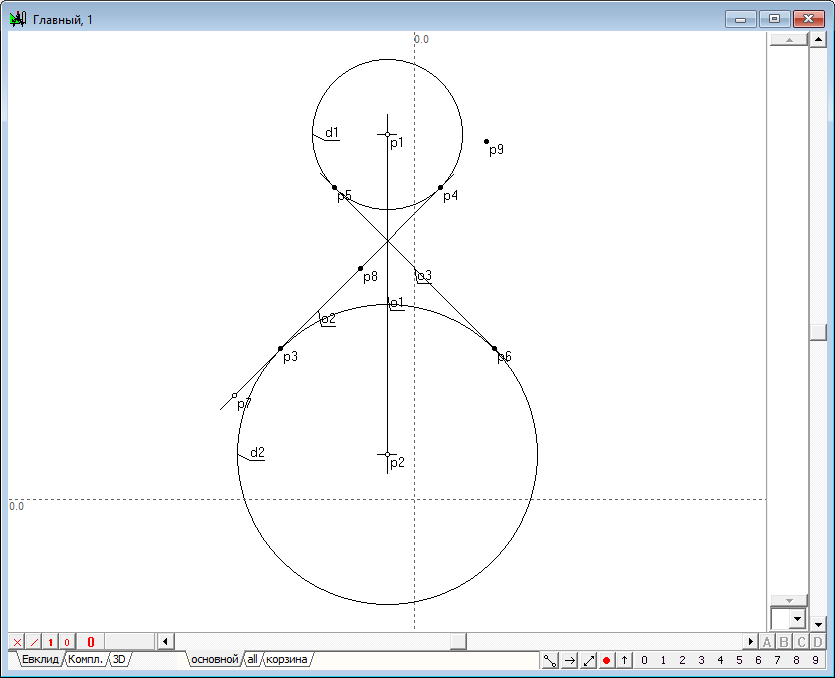
| 37 | Линии o2 и o3 можно понимать, как очерковые образующие конуса, касательного к исходным сферам. Будем считать линию o2 также проекцией плоскости сечения искомой квадрики, занимающей проецирующее положение. Это значит, что коника - сечение этой плоскостью искомой квадрики будет изображено в виде отрезка, лежащего на o2, а фокусы этой коники есть ни что иное, как точки p3 и p4. Зададим на прямой o3 управляющую точку и будем считать эту точку геометрическим местом пересечения директрисы коники с осью o2. Тогда не составит труда отыскать и точку пересечения второй директрисы с коникой. Выполним следующие построения: - удерживая нажатой клавишу Ctrl щелчком левой кнопки мыши разместим точку p7 на прямой o2; - выделим точки p3 и p4 и нажатием на клавишу c построим центр симметрии этих точек; - выделим последовательно точки p7 и p8 и нажатием на клавишу с латинским символом x найдем точку p9 - пересечение второй директрисы с осью коники.
Рис. 36 |
|
| 38 | Как мы уже видели в предыдущей задаче, очерк искомой квадрики должен пройти через двойные точки инволюции, заданной директориальными и фокусными точками на прямой. Для того чтобы их найти, выделим последовательно точки p7, p3, p4 и p9, а также прямую o2, нажмем на клавиатуре клавишу с латинским символом k, чтобы определить инволюцию pr1 и вслед за этим на клавишу с латинским символом p, в результате чего найдем двойные точки инволюции pr1 - точки p11 и p12.
Рис. 37 |
|
| 39 | Добавим к выделению прямую o1 и нажмем на клавишу с латинским символом x, в результате чего мы будем иметь точки, симметричные найденным. Итого, мы имеем четыре точки, через которые должен пройти очерк искомой квадрики.
Рис. 38 |
|
| 40 | Пятую точку можно найти, например, выполнив пересечение горизонтальной линии, проведенной через точку p9 с окружностью d1, для чего выделим точку p9, нажмем на клавишу с латинским символом h, затем добавим к выделению окружность d1 и нажмем на клавишу с латинским символом p. Получим точки p15 и p16, любую из которых теперь можно использовать для построения очерка искомой квадрики.
Рис. 39 |
|
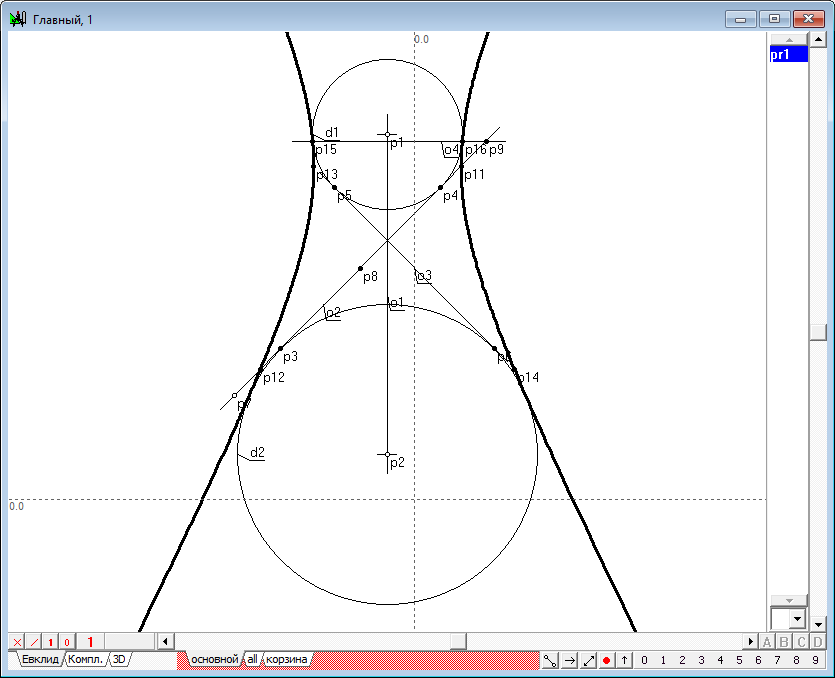
| 41 | Выделим точки p12, p14, p11, p13 и p15 и нажмем на клавишу с латинским символом y, для того чтобы построить конику y1 - очерк искомой квадрики. Понятно, что квадрика управляется однопараметрическим множеством точек p7, занимающим различные положения на прямой o2. Из построения видно - что все квадрики представляют собой пучок, индуцированный двумя произвольными сферами.
Рис. 40 |
|
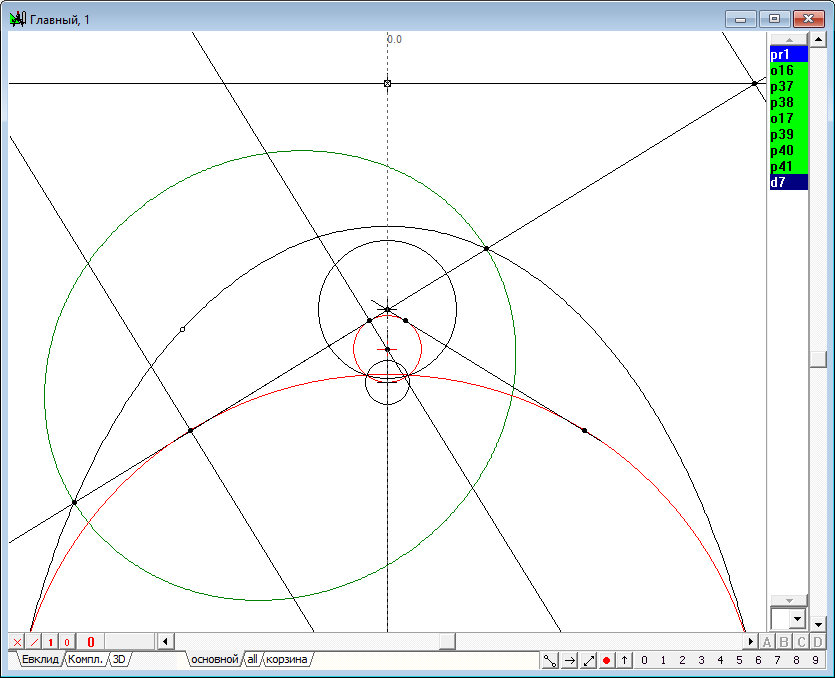
| 42 | Нажав на клавишу с латинским символом f, найдем фокусы и директрисы коники-очерка.
Рис. 41 |
|
| 43 | Зафиксируем положение полученных точек, оставив только их в выделении, нажав на клавишу с символом =, что приведет к образованию свободных точек-копий p19, p20 с координатами, равными текущим координатам точек p17 и p18.
Рис. 42 |
|
| 44 | Повторим это действие еще пару раз, смещая точку p7 таким образом, чтоб кривая y1 сохраняла вид гиперболы, главная действительная ось которой совпадает с линией соединения центров исходных сфер.
Рис. 43 |
|
| 45 | Выделим теперь точки p19, p20 и p21 и нажмем на клавишу с латинским символом g, что приведет к построению окружности d3, которая пройдет не только через эти точки, но и через остальные только что зафиксированные копии фокальных точек. В трехмерном пространстве эти точкам будут соответствовать фокальные окружности квадрики. Все же семейство пучка коник, представленных гиперболами, проходящих касательно к двум сферам образует в пространстве сферу, моделируемую на чертеже очерком-окружностью d3. Обратим внимание на то, что диаметр этой сферы определяется вершинами конусов, моделируемыми точками пересечения общих касательных к очеркам исходных сфер. Одна такая точка - p27 может быть построена за счет пересечения прямых o2 и o3. Для построения второй точки - p32 надо выделить окружности d1 и d2 и нажать на клавиши с символами o (нижний регистр), 8 и p.
Рис. 44 |
|
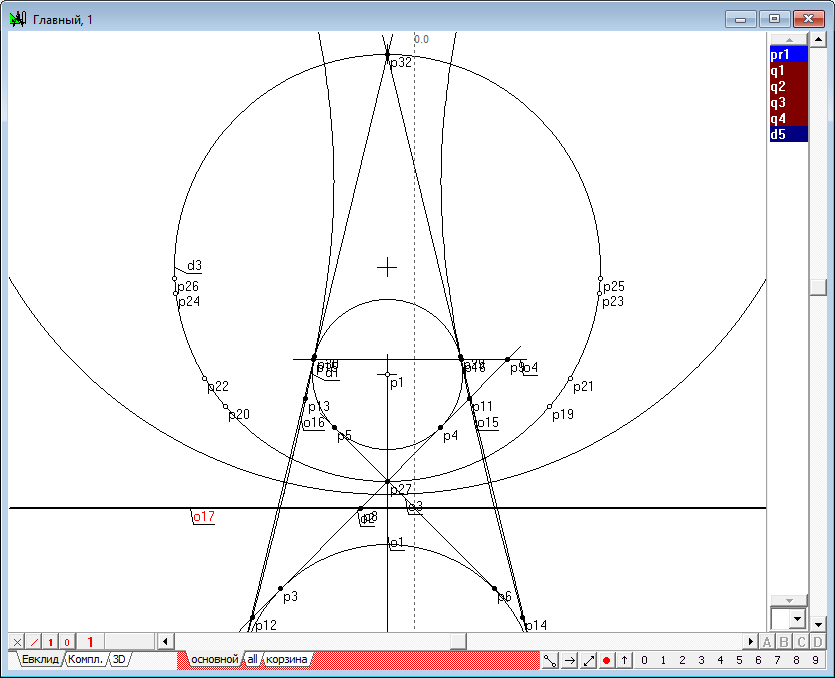
| 46 | Восстановив сферы инверсии для исходных сфер, заданных очерками d1 и d2 (выделим их и нажмем на клавишу с символом R), обнаружим, что сфера, построенная на множестве фокальных окружностей и представленная очерком d3 проходит через центр одной и сфер инверсии - точку p32. Это означает, что такая сфера, преобразованная в инверсии перейдет в плоскость, которая моделируется радикальной прямой o17, построенной для окружностей d1 и d2 (выделим их и нажмем на клавишу с символом r).
Рис. 45 |
|
| 47 | Если же очерки квадрики примут эллиптическую форму или же главная собственная ось гиперболы станет перпендикулярной линии соединения центров исходных сфер, то их фокусы станут перемещаться по прямой o1. | |
| 48 | Отменим сделанные построения, нажимая комбинацию клавиш Ctrl+Z до того состояния, когда очерк коники будет представлять гиперболу с главной осью, совпадающей с прямой o1, а его фокусы будут представлены точками p17 и p18. Найдем точки пересечения прямой o1 с окружностью d1 - p19 и p20, а затем точки пересечения прямой o1 с окружностью d2 - точки p21, p22. Зададим две инволюции pr2 и pr3 следующим образом:
Рис. 46 |
|
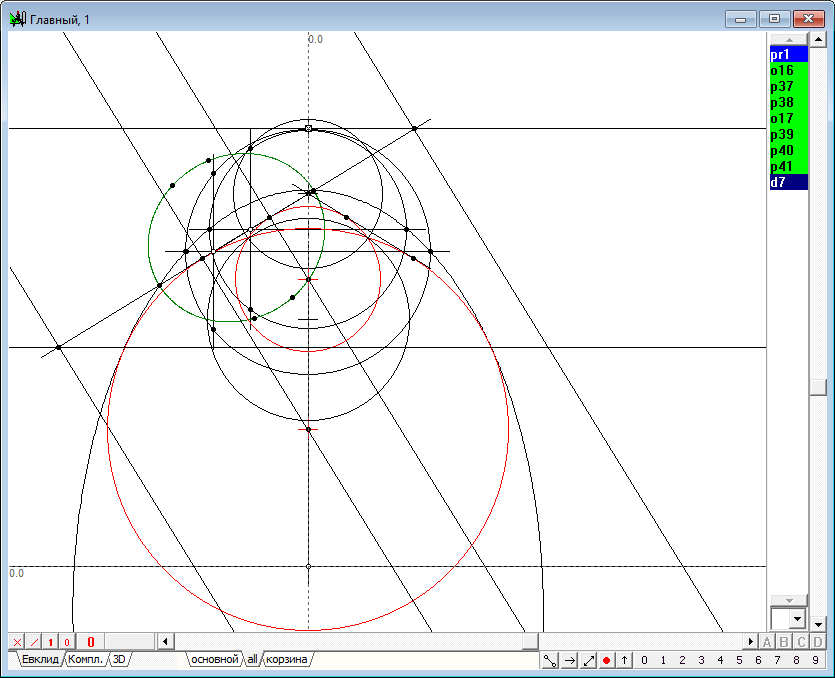
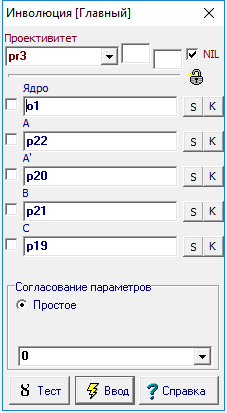
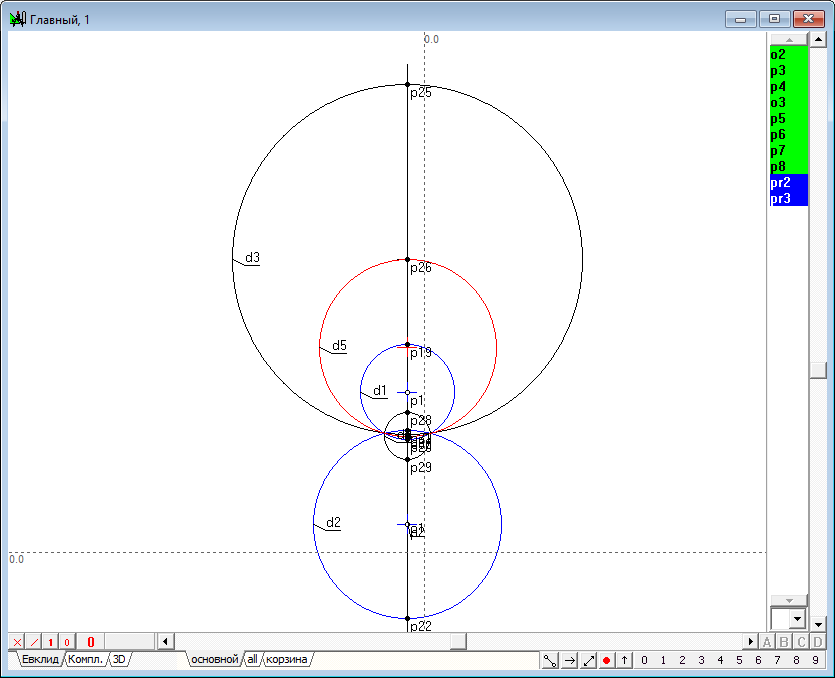
| 49 | Найдем двойные точки проективитета pr2, для чего выделим его метку и нажмем на клавишу с символом p. Не снимая выделения, проведем через полученные точки p24 и p25 окружность d3, нажав на клавишу D (верхний регистр) и найдем ее центр p26, нажав на клавишу с символом c. То же самое сделаем со вторым проективитетом, в результате чего построим действительный центр p30 мнимой окружности d4. Проведя еще одну окружность d5 через точки p26 и p30, констатируем, что эта окружность является геометрическим местом точек, фокусов образующих гипербол - очерков квадрики. Обозначим очерки исходных сфер синим цветом, а очерк "фокальной" сферы красным цветом.
Рис. 47 |
|
| 50 | Будем постепенно смещать шейпером центр p1 окружности d1 в направлении центра окружности d2. В определенный момент, когда окружности начнут пересекаться в действительных точках, общие "внутренние" касательные окружностей исчезнут. Однако это не приведет к тому, что очерк квадрики нельзя будет построить, так как в нашем распоряжении имеются внешние касательные, их можно провести и использовать для построения очерка таким же образом, как и в случае использования внутренних касательных. Этот факт подтверждается и наличием действительной окружности d5, изображенной красным цветом.
Рис. 48 |
|
| 51 | Однако наибольший для исследования интерес представляет случай, при котором окружность d1 полностью находится внутри окружности d2. Наличие красной окружности d5, дает основание к тому, чтобы заключить, что фокусы образующих квадрики по-прежнему существуют, а значит, существуют и сами квадрики. Однако отсутствие общих касательных у вложенных окружностей позволяет предположить, что мы имеем дело с проявлением свойств мнимых образов в задаче Данделена. Исследование этой проблемы пока не завершено. |