|
||
| Back to the task list | ||
| The information presented in this lesson task is implemented in a software system Simplex | ||
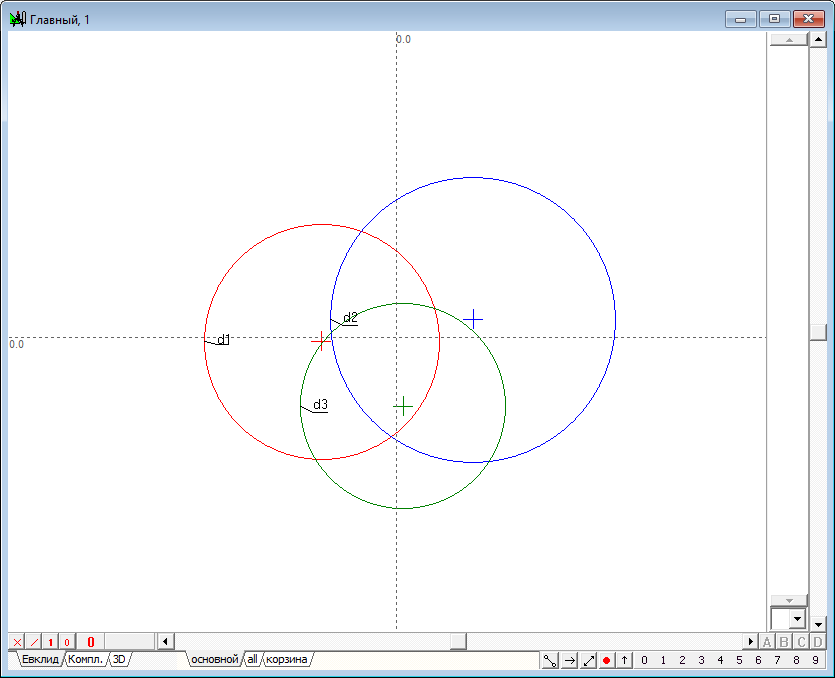
| 1 | Now we solve the problem of Apollonius to construct a circle tangent to three given, based on the concept of an orthogonal imaginary circle, discussed in the previous lesson. Start a new project. Let three circles sre given the plane, which are clearly disjoint.
Fig. 1 |
|
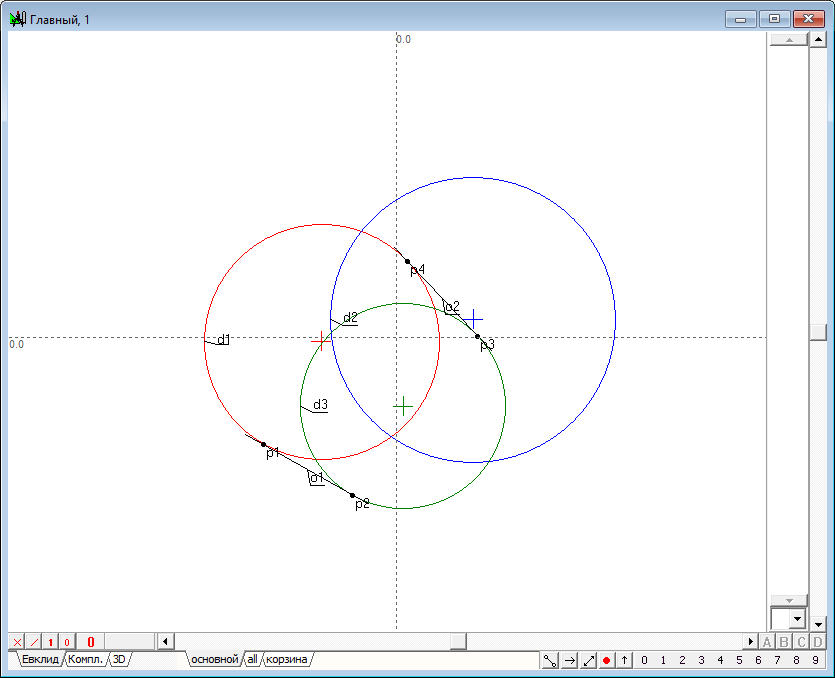
| 2 | Construct tangents o1 and o2 to circles d1 and d3.
Fig. 2 |
|
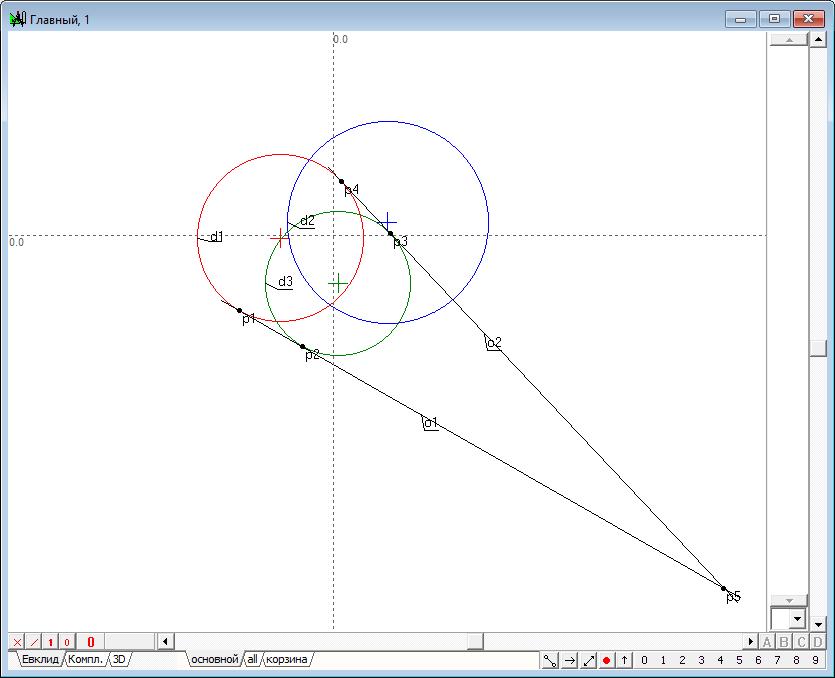
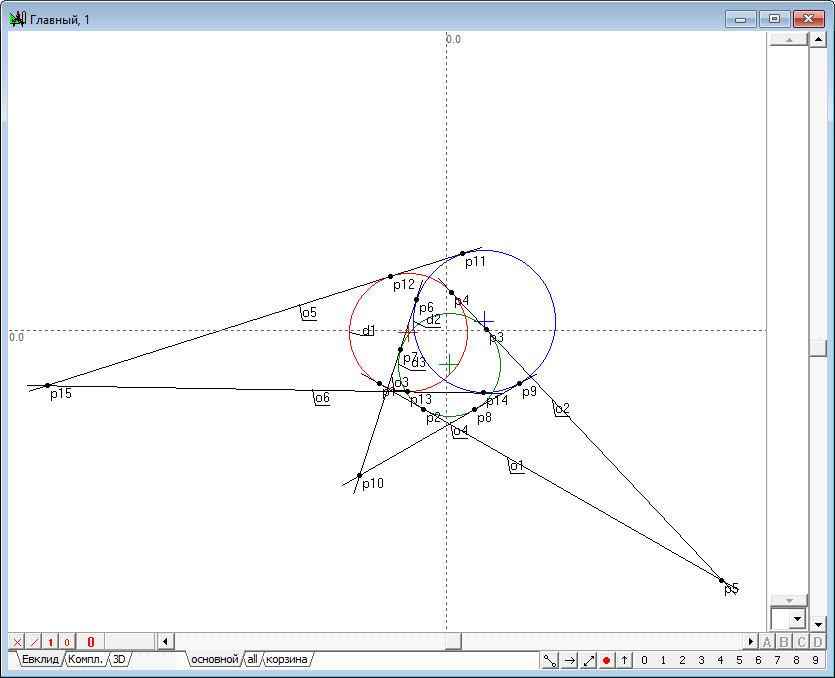
| 3 | Find the intersection point p5 of the tangents o1 and o2.
Fig. 3 |
|
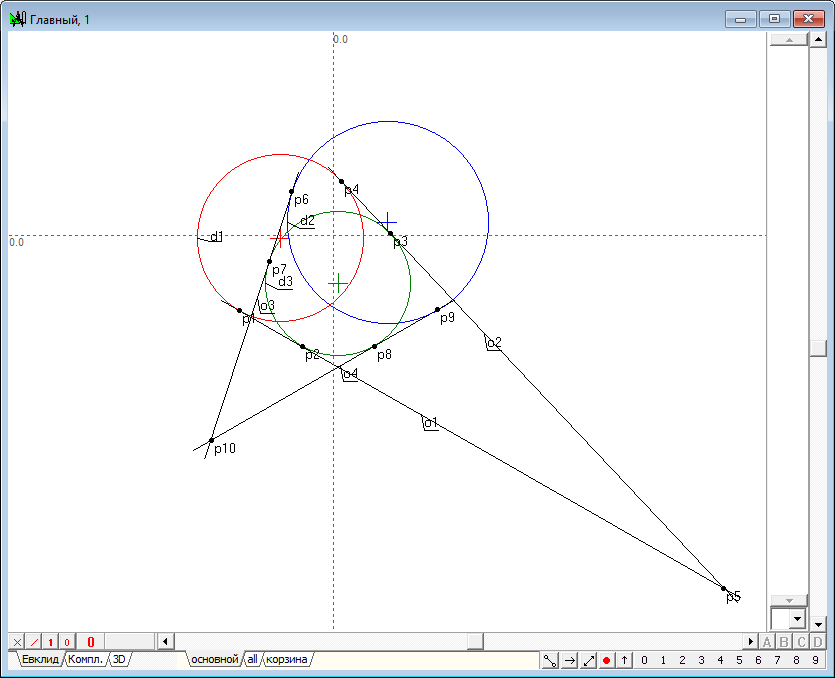
| 4 | Construct the intersection point p10 tangent to circles d2 and d3.
Fig. 4 |
|
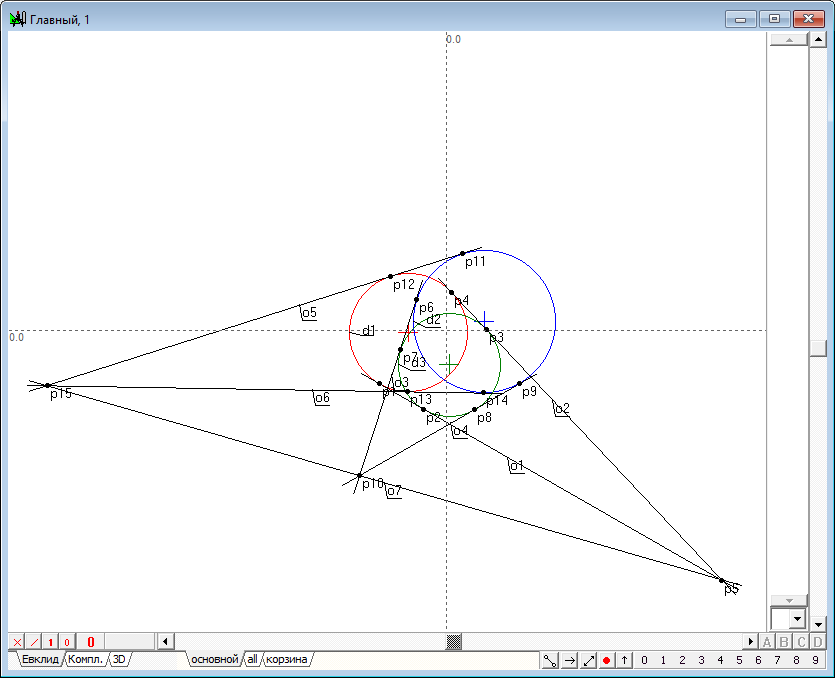
| 5 | Construct the intersection point p15 tangent to circles d1 and d3.
Fig. 5 |
|
| 6 | Draw a straight line o7 passing through the three points p5, p10 and p15. To do this, select the point and press the button with the Latin symbol q.
Fig. 6 |
|
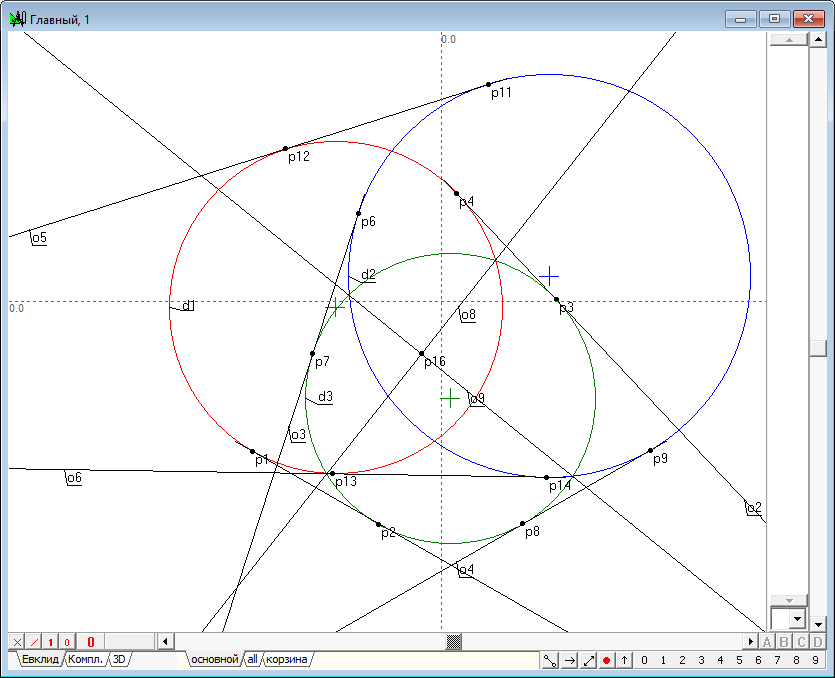
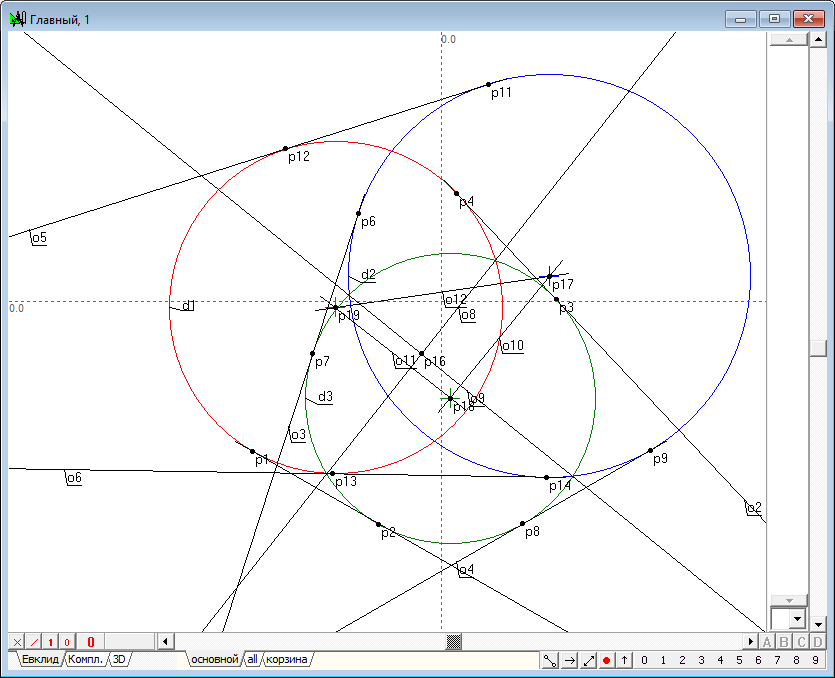
| 7 | Find the radical center of three circles - point p16.
Fig. 7 |
|
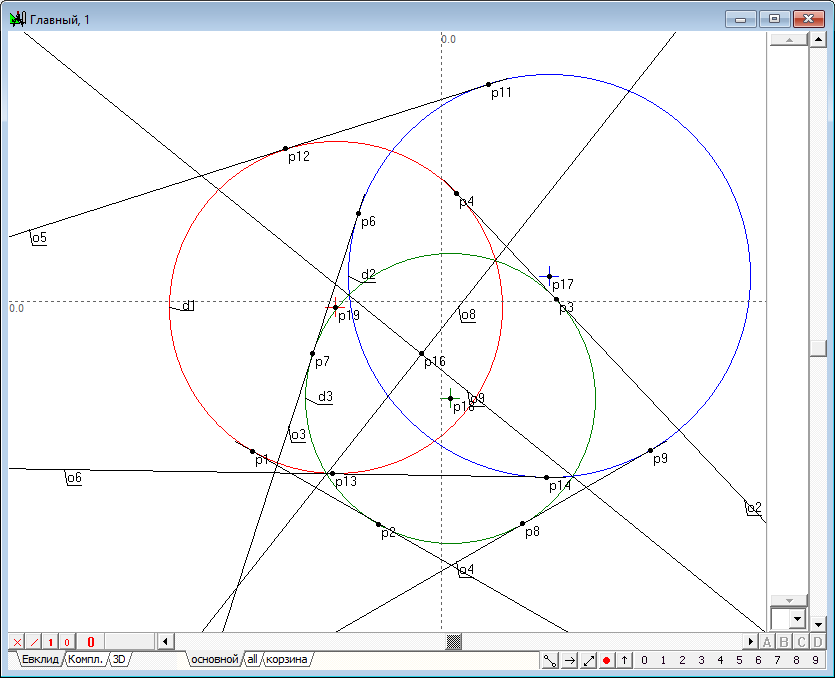
| 8 | Determine the center of the original circle - points p17, p18, p19.
Fig. 8 |
|
| 9 | Construct triangle with sides o10, o11, o12 based on points p17, p18, p19
Fig. 9 |
|
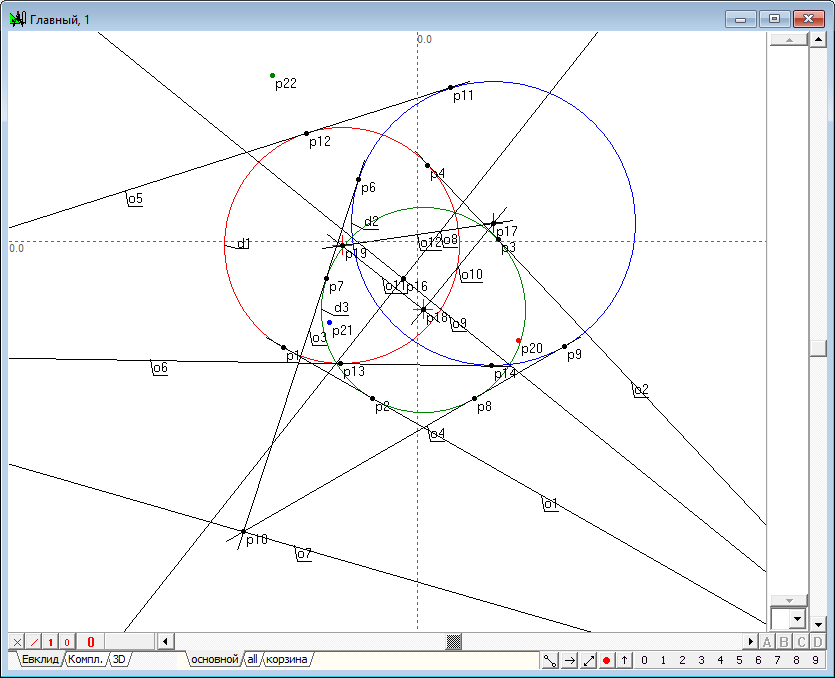
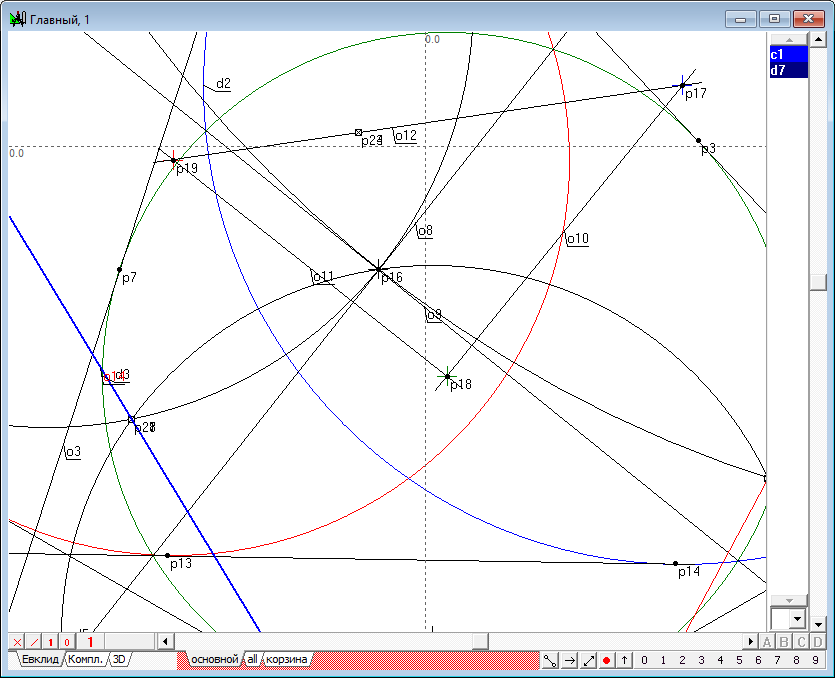
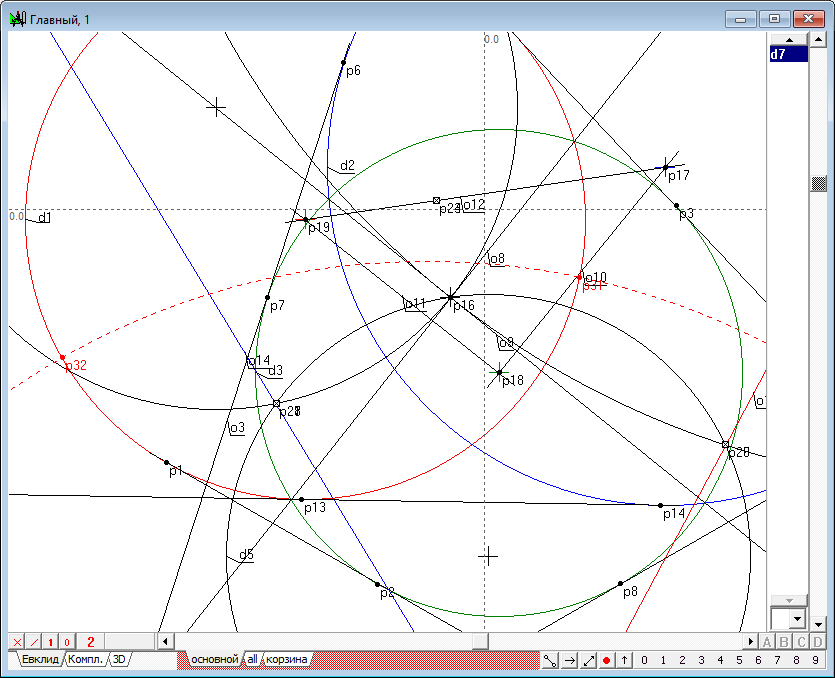
| 10 | Map the radical center p16 in the inversion circles d1, d2 and d3. We get the points p20, p21, p22.
Fig. 10 |
|
| 11 | Draw circles d4, d5, d6 passing trough the radical center and all possible pairs of a triad of points p20, p21, p22 .
Fig. 11 |
|
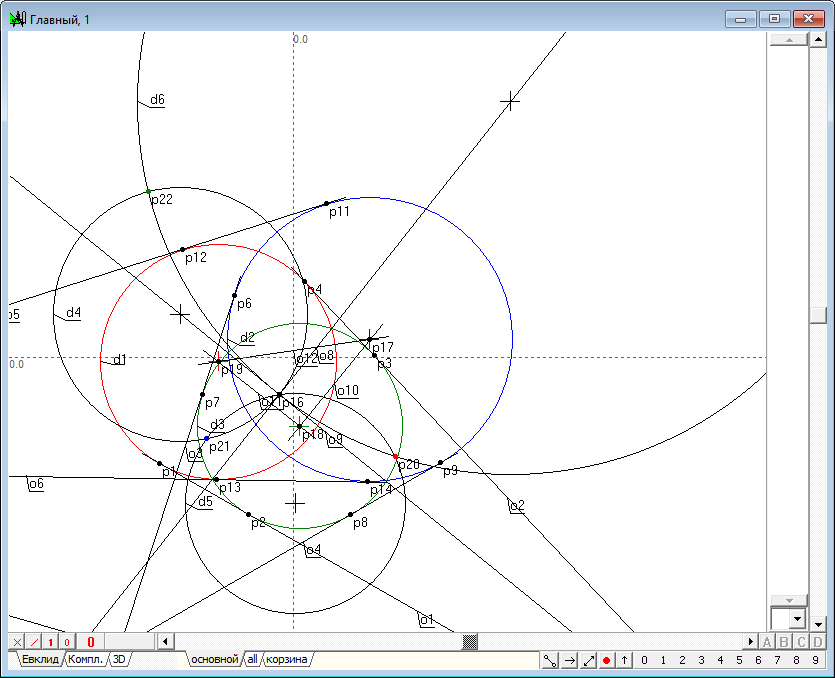
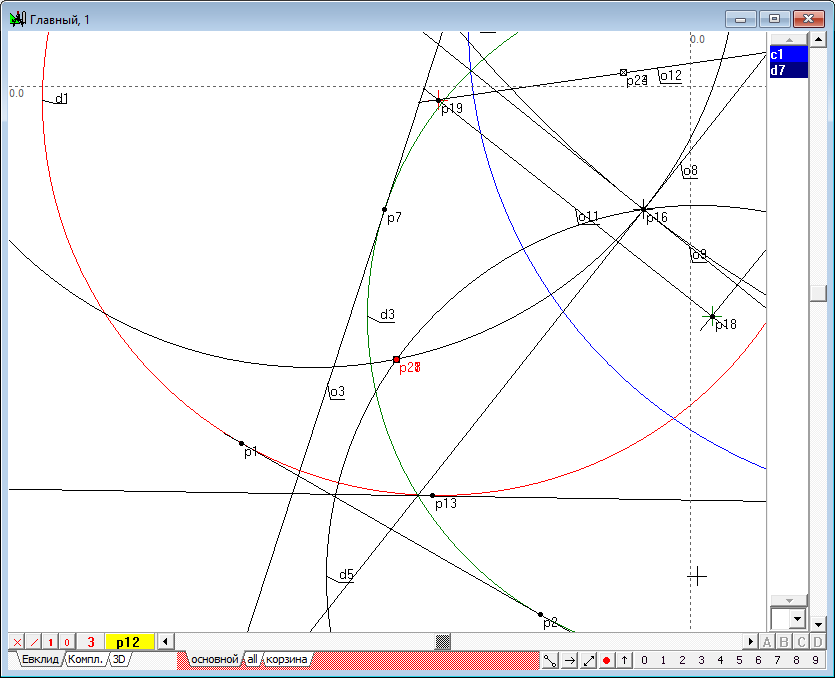
| 12 | Find the points p23 and p24 of intersection of the line o12 and d5 circle.
Fig. 12 |
|
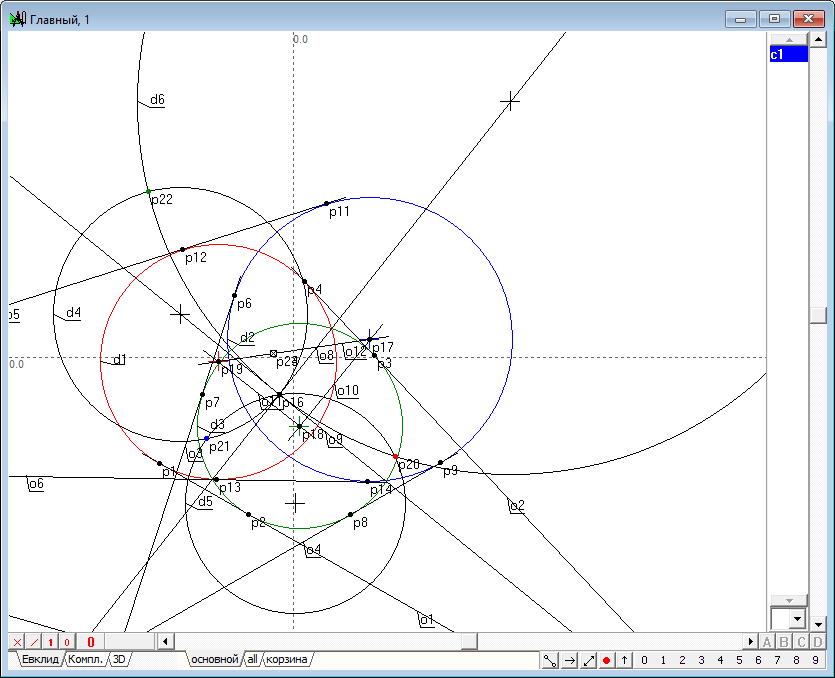
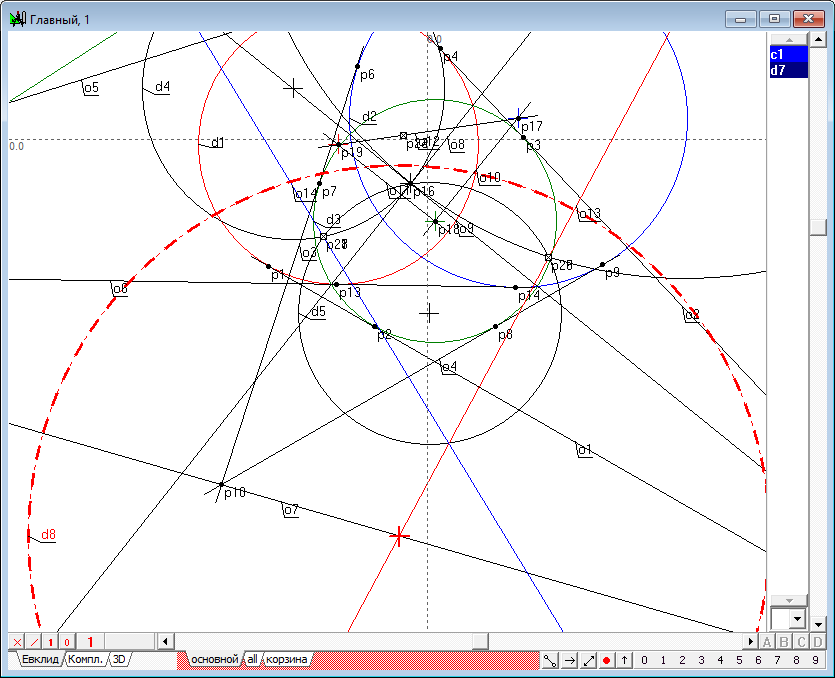
| 13 | Calculate the radius of the imaginary circle orthogonal finding the distance c1 between the radical center point p16 and the point p24.
Fig. 13 |
|
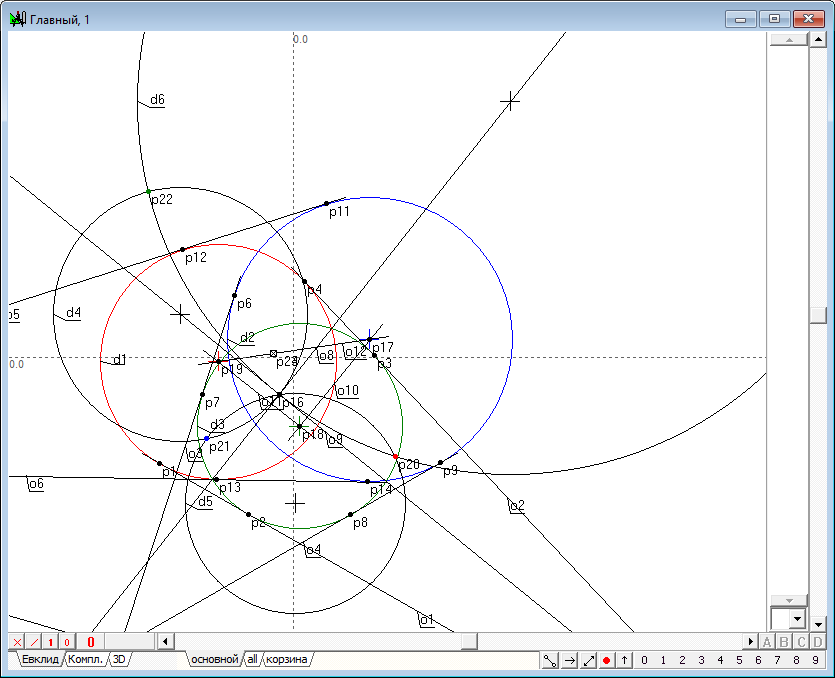
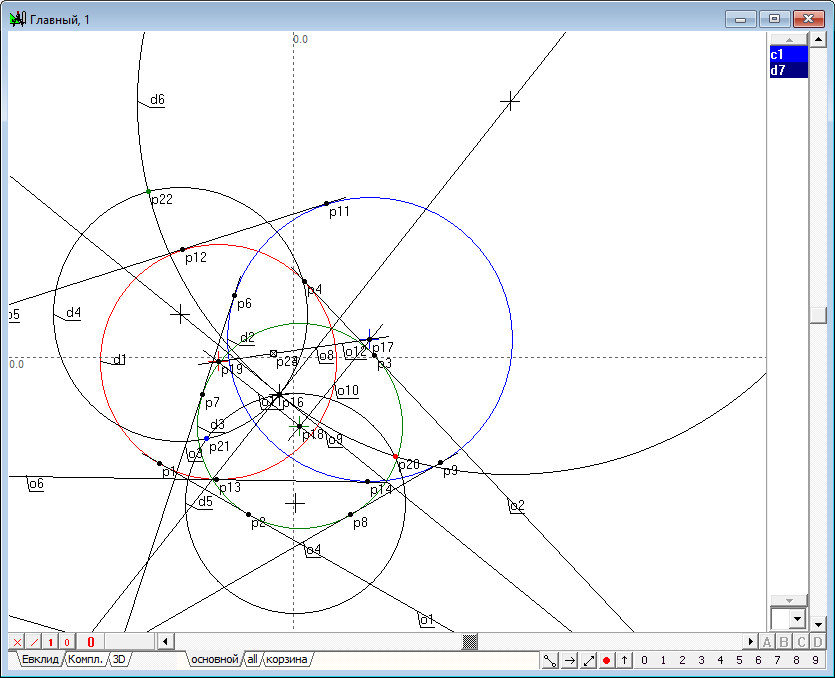
| 14 | Define an imaginary circle d7 with real center of p16 and the value c1.
Fig. 14 |
|
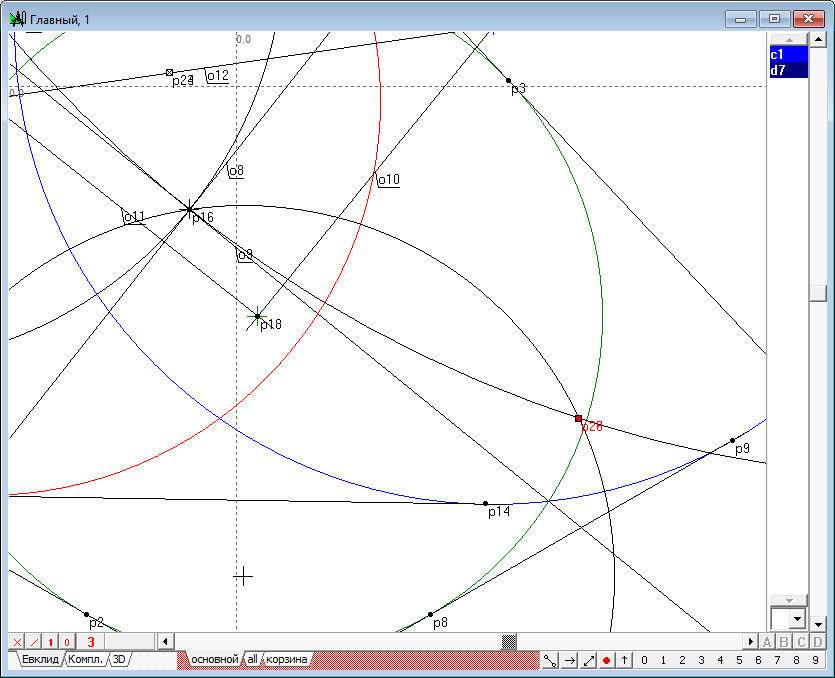
| 15 | Points p25 and p26 are the intersection of circles d7 and d1.
Fig. 15 |
|
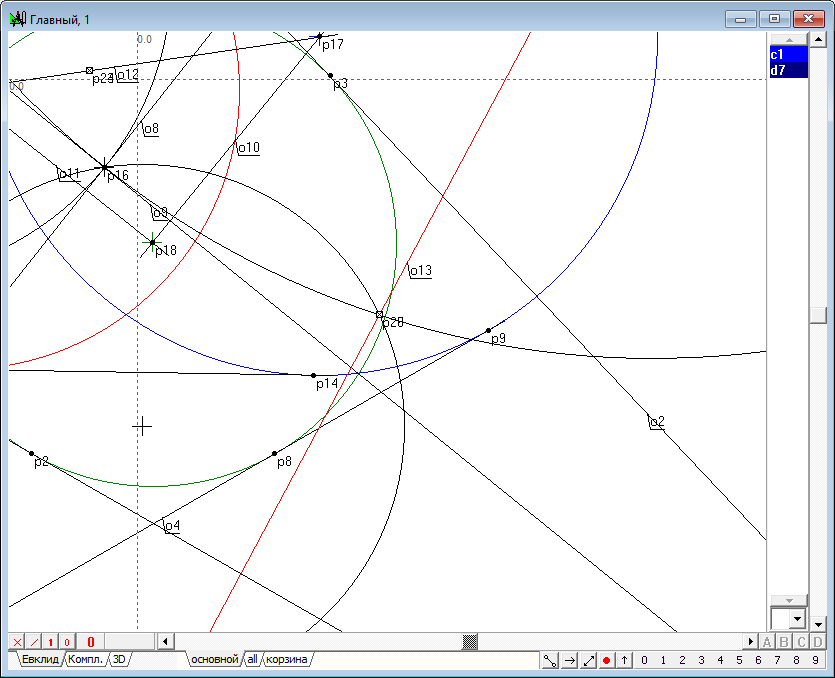
| 16 | Draw a straight line o13 passing through the points p25 and p26.
Fig. 16 |
|
| 17 | Points p27 and p28 are the intersection of circles d7 and d2.
Fig. 17 |
|
| 18 | Draw a straight line o14 passing through the points p27 and p28.
Fig. 18 |
|
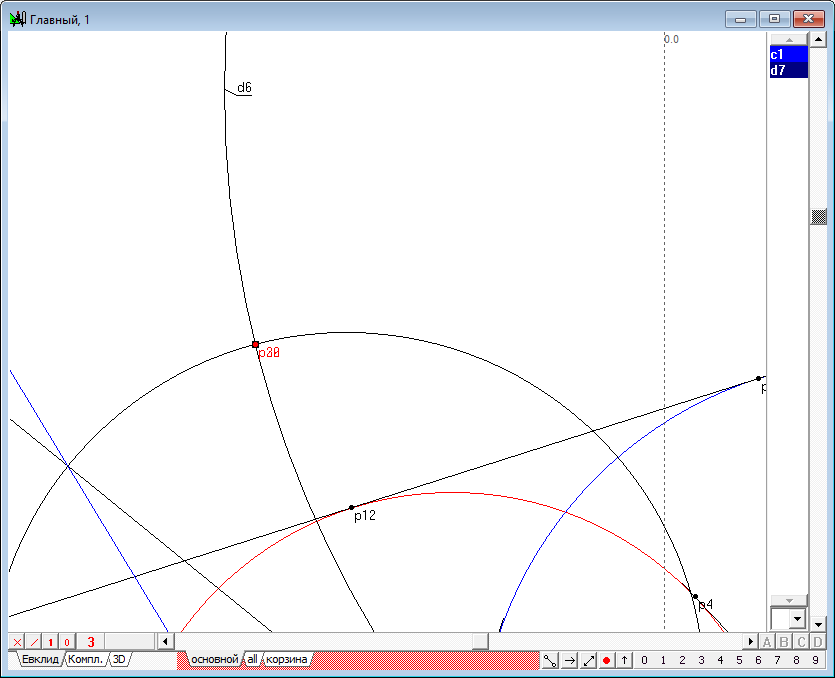
| 19 | Points p29 and p30 are the intersection of circles and d7 d3.
Fig. 19 |
|
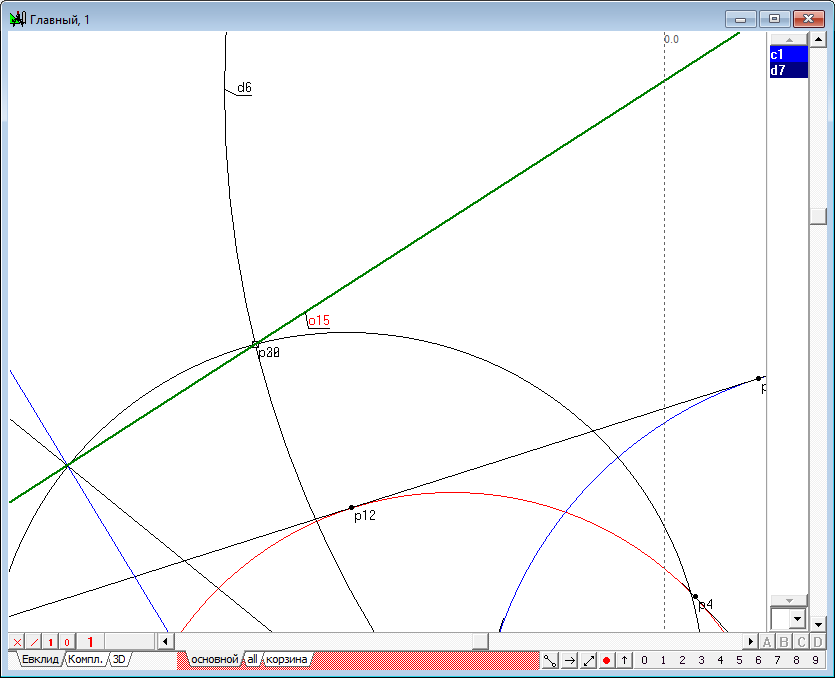
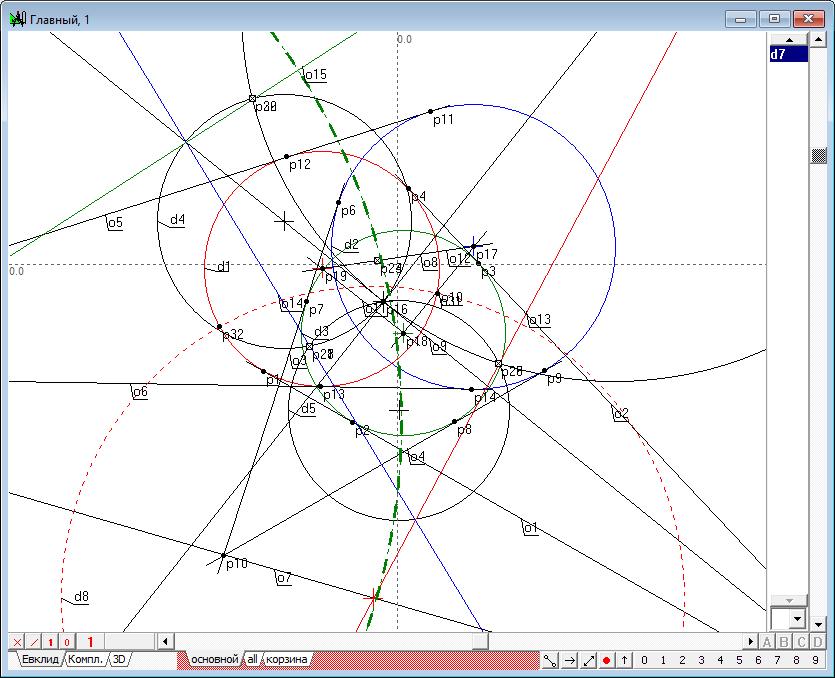
| 20 | Draw a straight line o15 passing through the points p29 and p30.
Fig. 20 |
|
| 21 | Construct a circle d8, passing perpendicular to the lines o13, o7 and circle d1.
Fig. 21 |
|
| 22 | Find the intersection points p31, p32 of circles d8 and d1.
Fig. 22 |
|
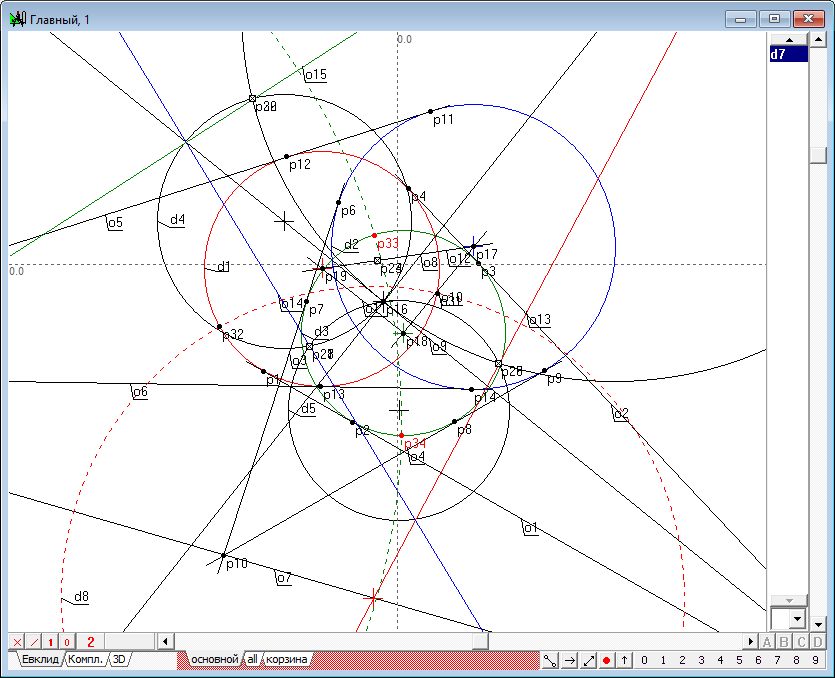
| 23 | Construct a circle d9, passing perpendicular to the lines o15, o7, and circle d3 .
Fig. 23 |
|
| 24 | Find the intersection points p33, p34 of circles d3 and d9.
Fig. 24 |
|
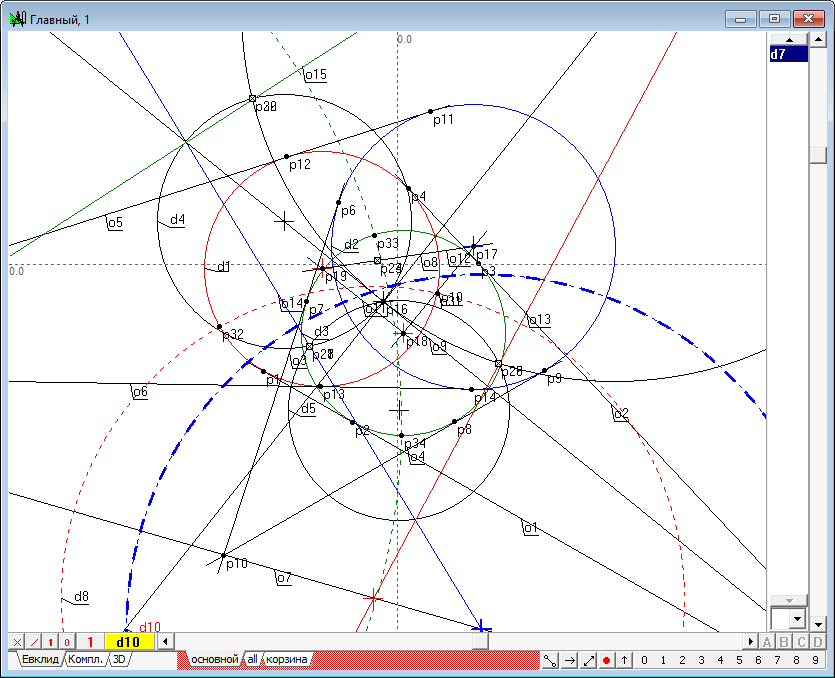
| 25 | Construct a circle d10, passing perpendicular to the line o14, o7 and circle d2.
Fig. 25 |
|
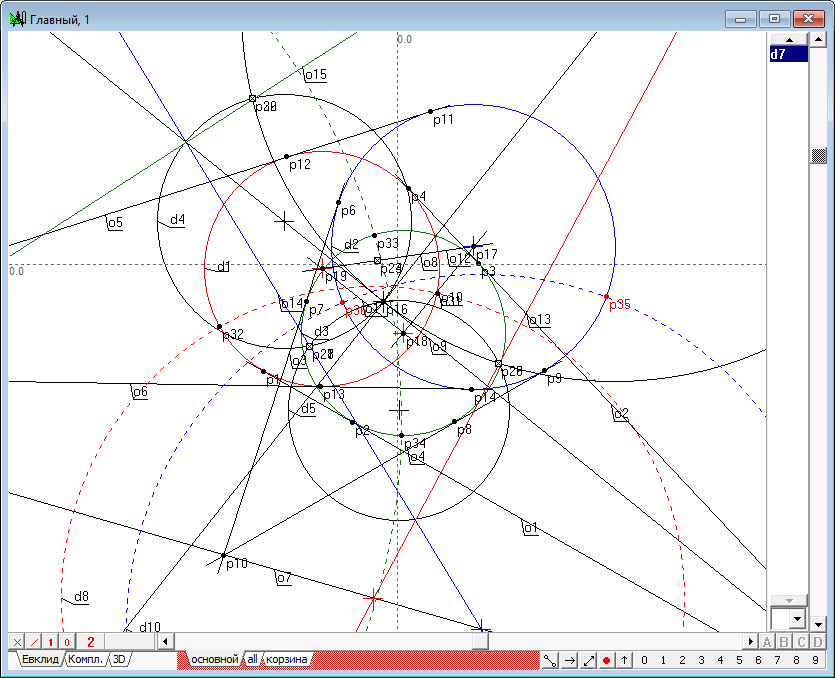
| 26 | Find the intersection points p35, p36 of circles d10 and d2.
Fig. 26 |
|
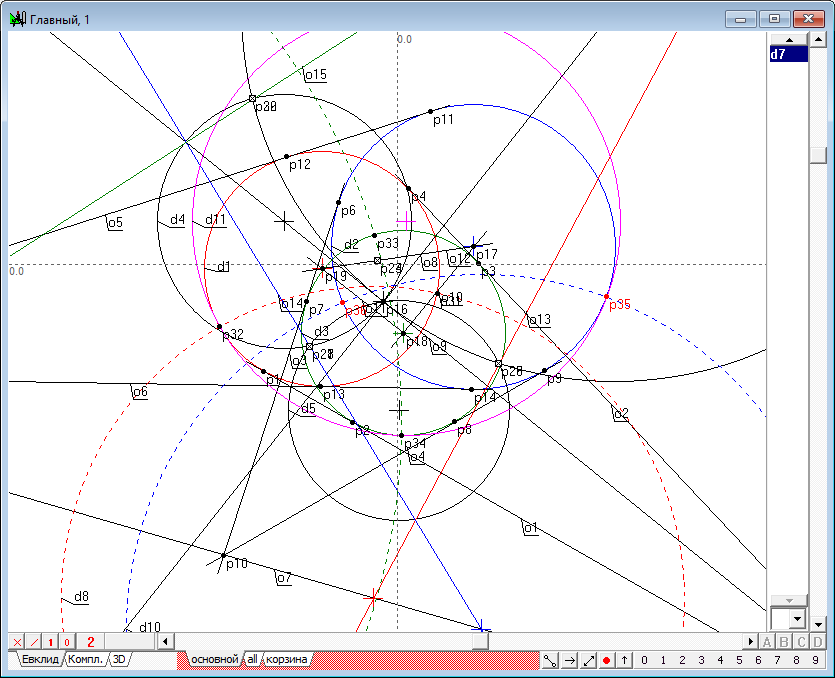
| 27 | Draw a circle d10, passing orthogonal to the lines o7, o14 and circle d2.
Fig. 27 |
|
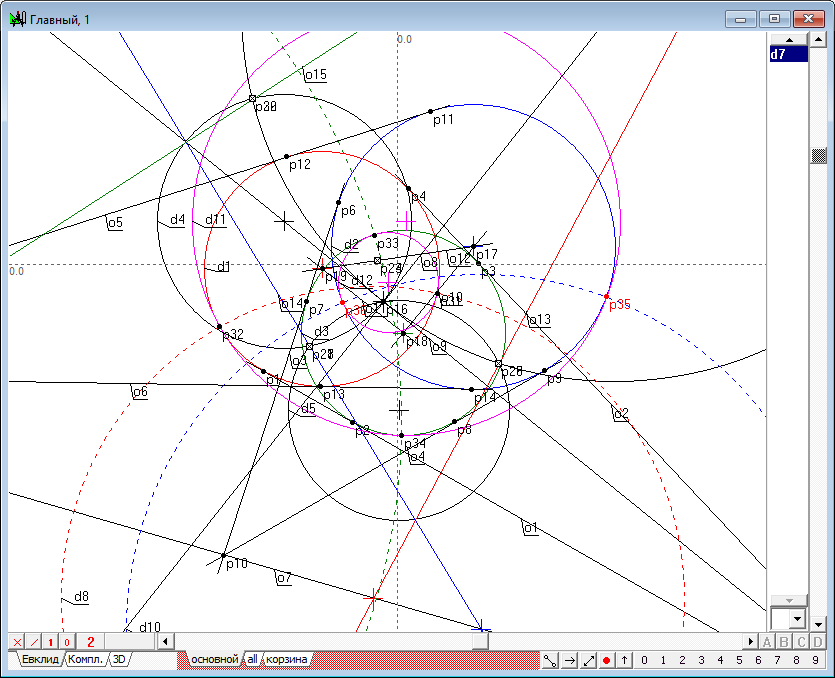
| 28 | Draw the desired d11 circle passing through the points p32, p34, p35 and d12 passing through the points p31, p36 and p33.
Fig. 28 |
|
| 29 |  |
|
| 30 |  |
|
| 31 |  |
|
| 32 |  |
|
| 33 |  |
|
| 34 |  |
|
| 35 |  |
|
| 36 |  |
|
| 37 |  |
|
| 38 |  |
|
| 39 |  |
|
| 40 | 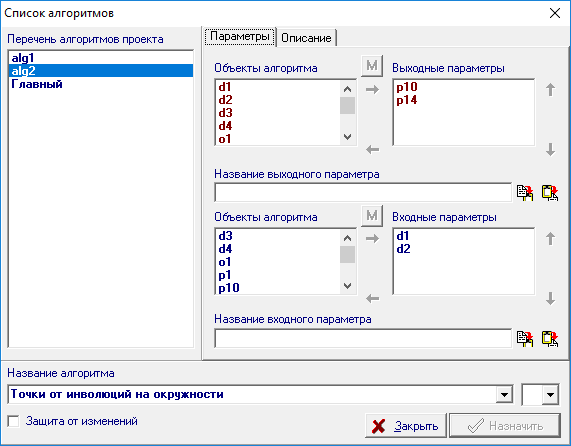 |
|
| 41 | 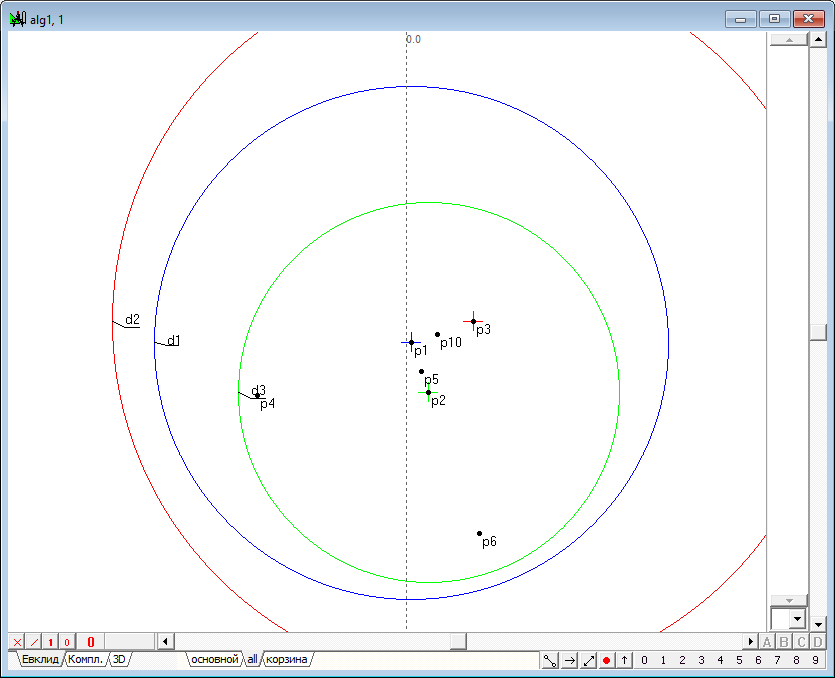 |
|
| 42 | 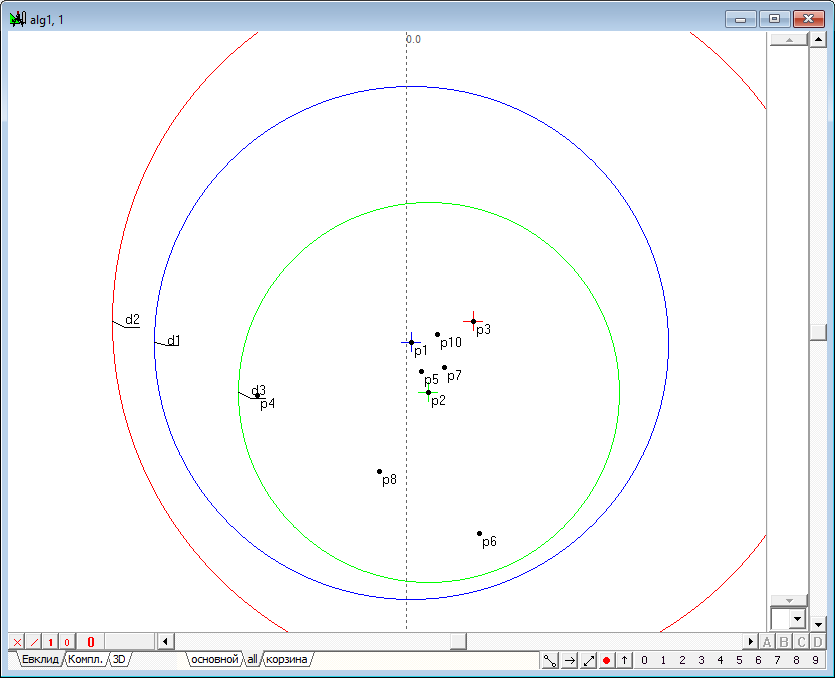 |
|
| 43 | 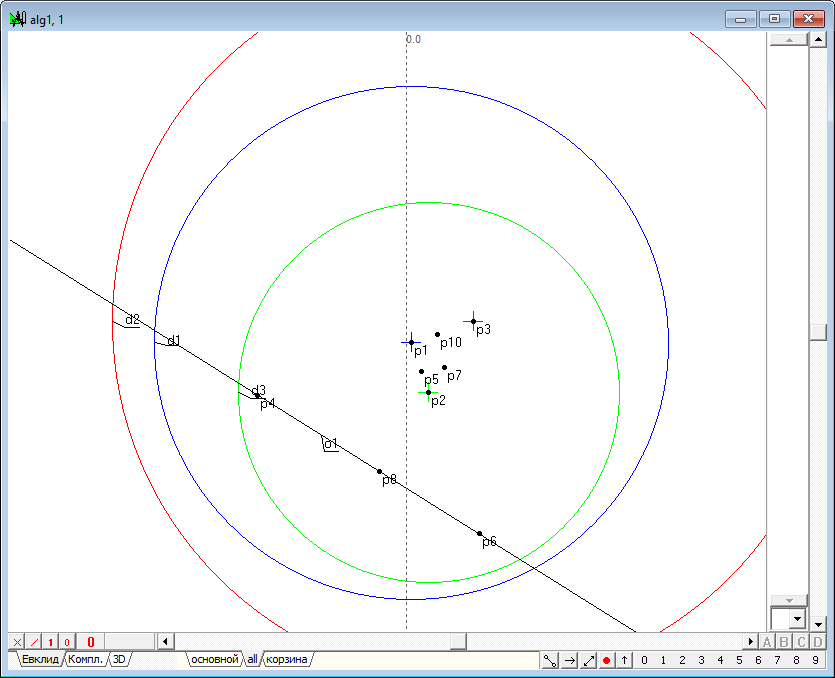 |
|
| 44 | 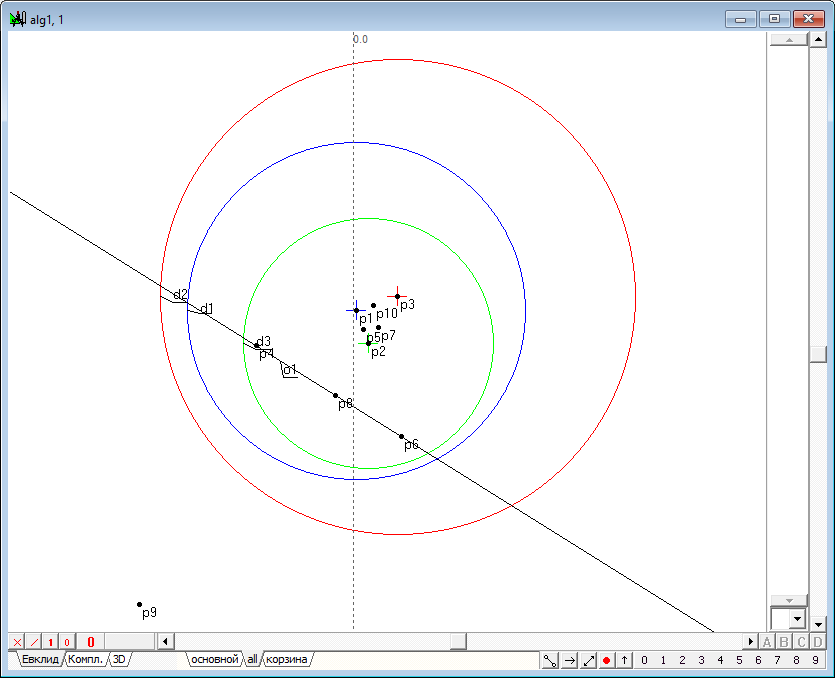 |
|
| 45 |  |
|
| 46 |  |
|
| 47 |  |
|
| 48 |  |
|
| 49 | 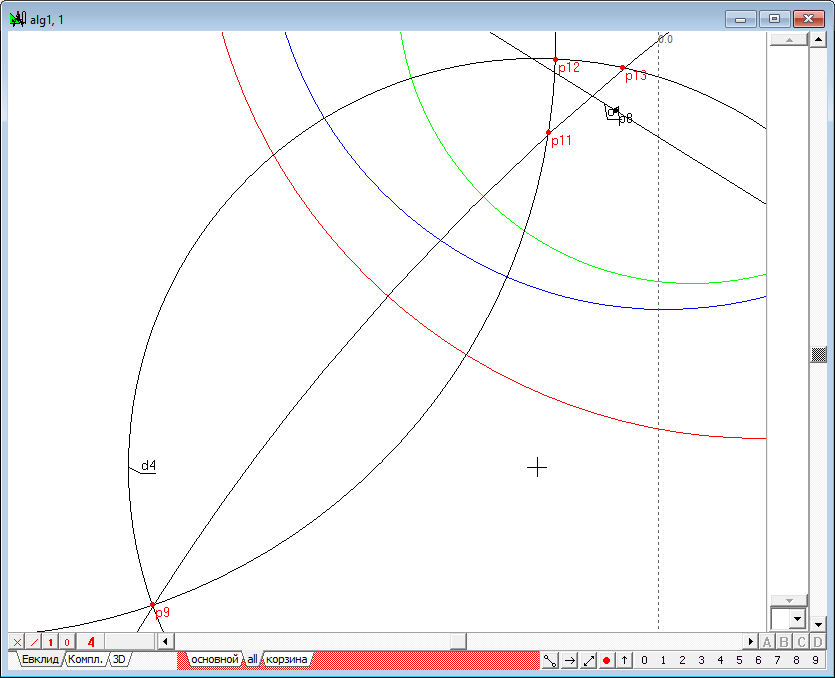 |
|
| 50 | 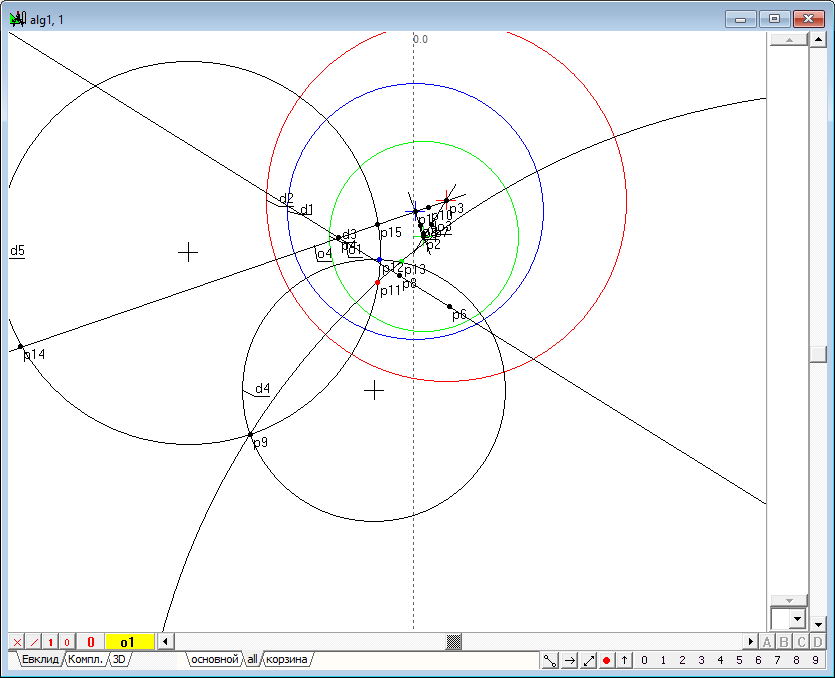 |
|
| 51 | 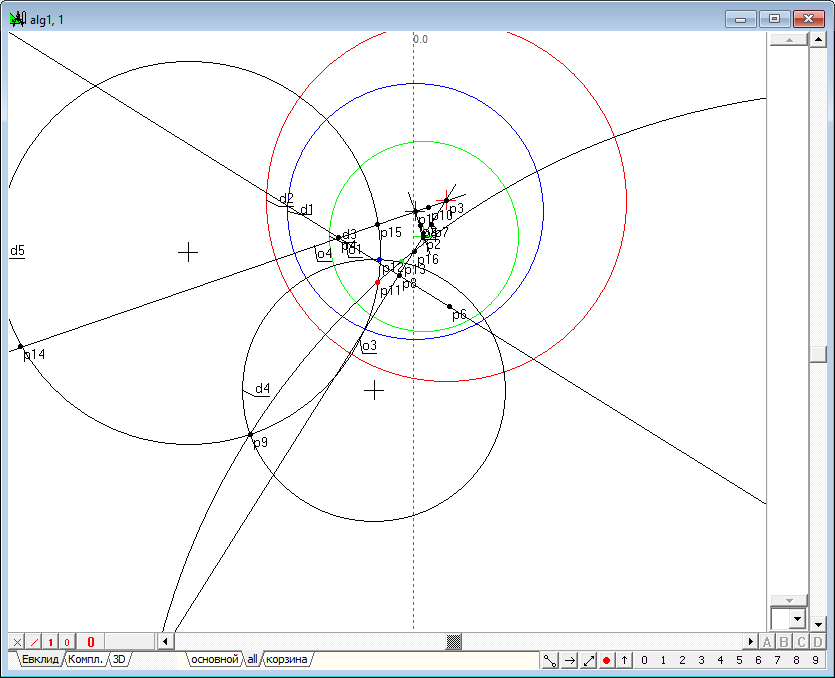 |
|
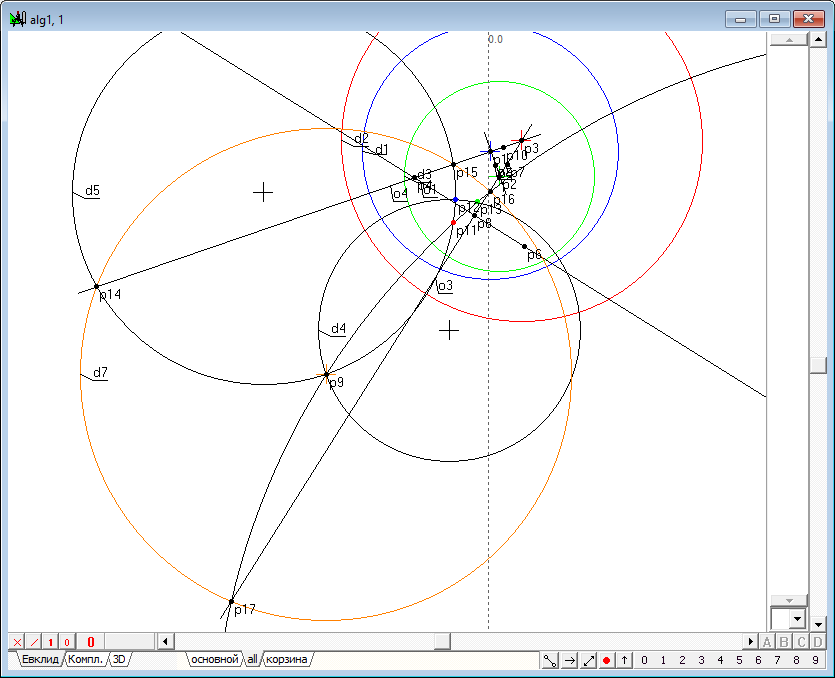 |