|
||
Условие задачи Аполлония исключительно просто: пусть на плоскости даны три окружности. Построить с помощью циркуля и линейки пару окружностей, касательные к ним. Всего можно построить восемь касательных окружностей (четыре пары). При некоторых взаимных положениях исходных окружностей касательные окружности построить невозможно (имеется в виду действительные окружности, если считать окружности мнимыми, то окружностей всегда будет восемь, кроме, быть может, вырожденных случаев). Решение задачи обычно находят следующим образом: выбирают среди окружностей минимальную и уменьшают радиусы всех исходных окружностей на величину радиуса этой окружности. Тогда выбранная окружность "стягивается" в точку, а две оставшиеся уменьшаются в радиусе. Затем решают более простую задачу: построить окружность, проходящую через точку и касательную при этом к двум заданным прямым. После решения этой задачи полученную окружность увеличивают на радиус выделенной окружности, что приводит в конечном итоге к решению исходной задачи. Несмотря на то, что данное решение приводит к правильному результату, оно не вскрывает фундаментальных свойств плоскости, которые обнаруживаются за формулировкой задачи Аполлония. Полное понимание этих свойств требует обращения к понятиям проективной геометрии и преобразованию инверсии. Зададимся целью изучить эти свойства и найти такой единый способ решения задачи Аполлония, который не потребует измерения расстояний, а будет основан лишь на свойствах линий и окружностей проективной плоскости. К полному решению будем подходить постепенно, изучая при этом приемы работы в системе геометрического моделирования Симплекс. Итак, приступим к выполнению построений, не прибегающих к измерению и изменению радиусов окружностей. Избранный подход позволит нам распространить единый метод решения задачи не только на окружности, выбранные в качестве исходных данных, но и на точки и прямые линии в различных комбинациях. Рассуждения, применяемые в алгоритме решения задачи, будут одинаковыми и не будут зависеть от типов исходных объектов. Загрузим систему Симплекс, создадим новый проект, нажав на кнопку |
||
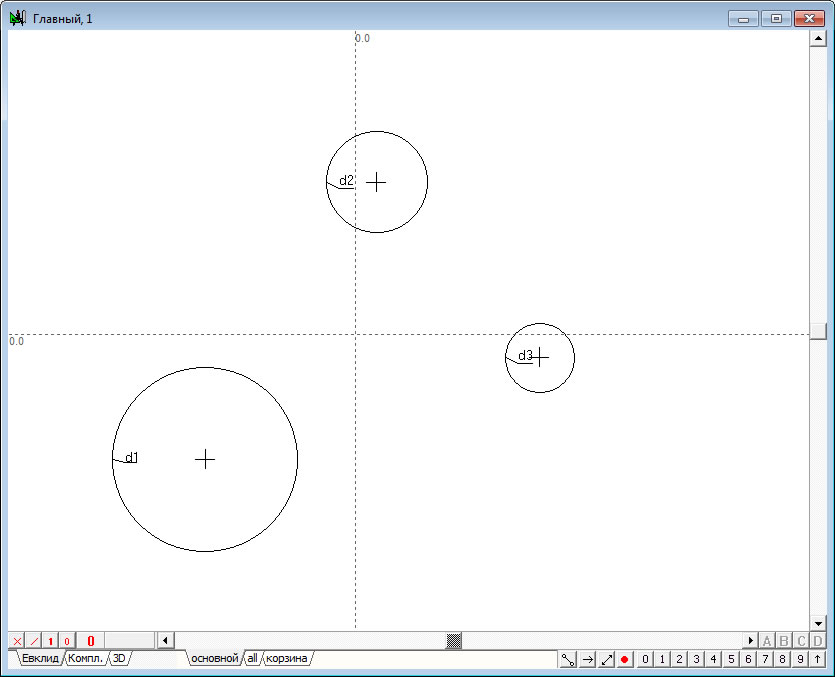
| 1. | Разместим на рабочем поле чертежа три окружности
,
и
. Для этого воспользуемся функцией «Свободная окружность», которую можно вызвать, нажав на кнопку |
|
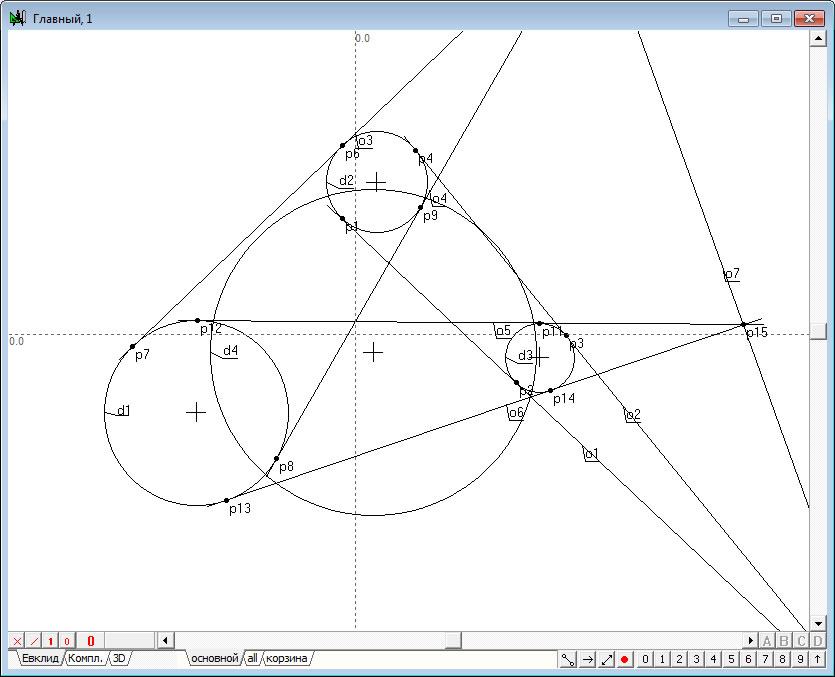
Рис. 1 |
||
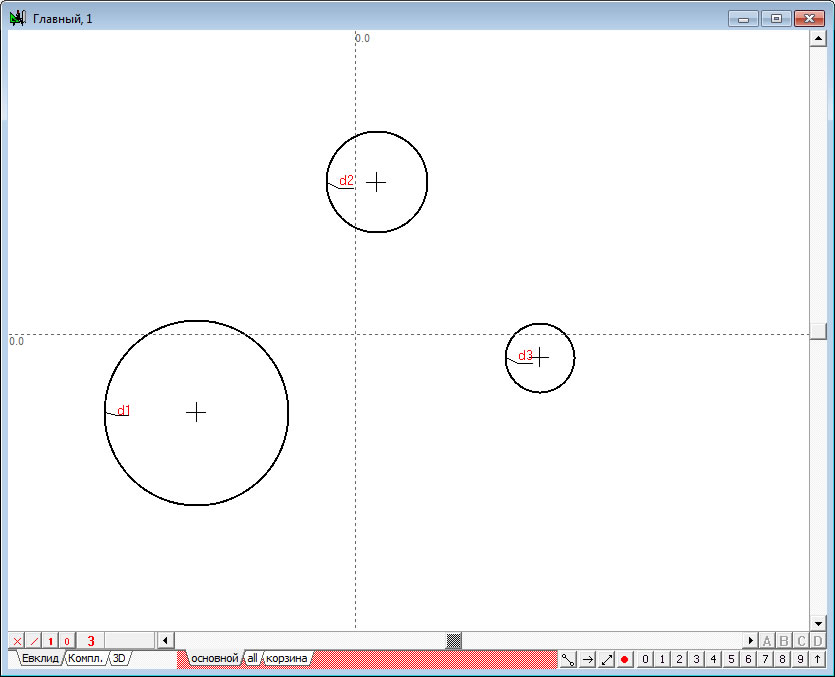
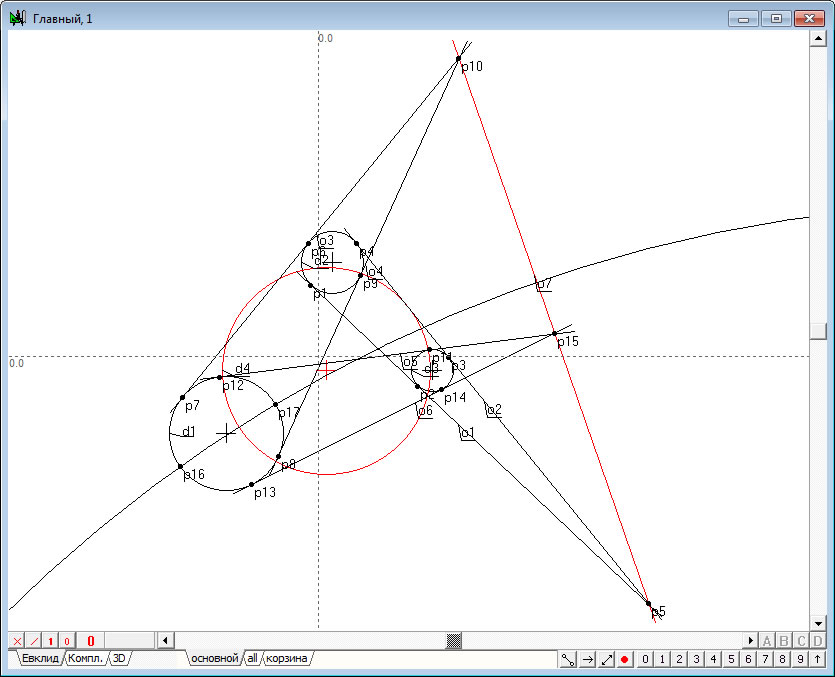
| 2. | Нажмем на клавишу Пробел, чтобы переключиться в режим выделения объектов курсором |
|
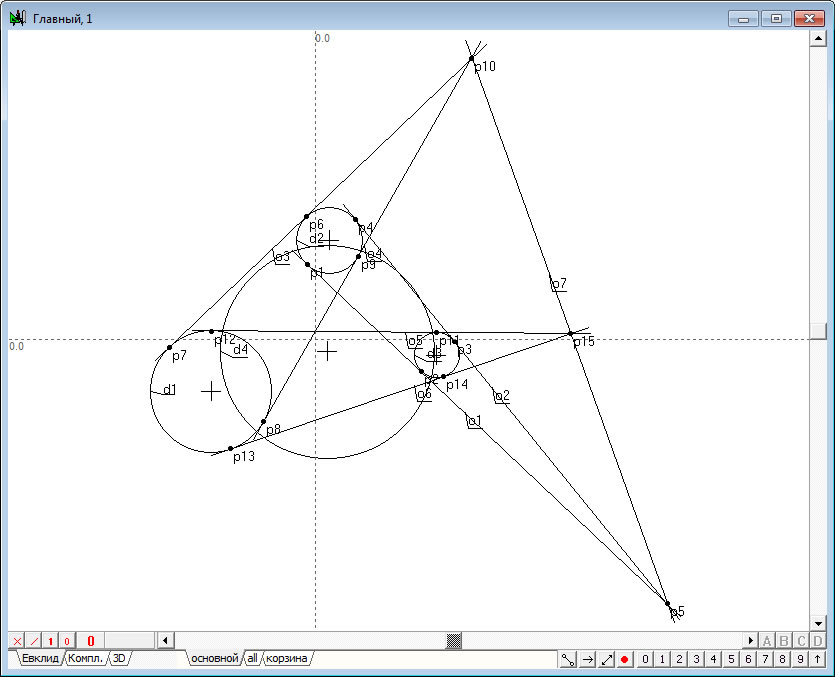
Рис. 2 |
||
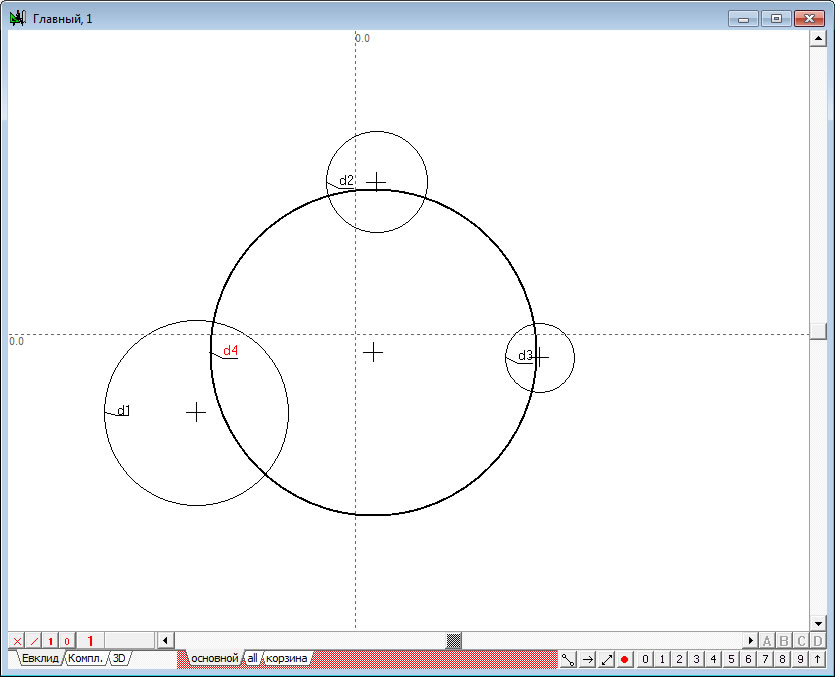
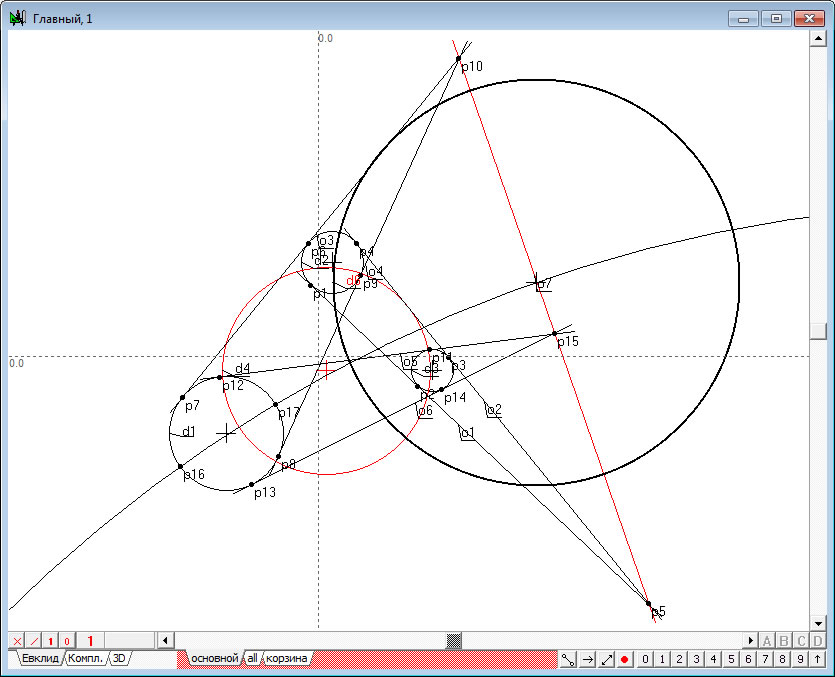
| 3. | Нажмем на клавиатуре кнопку, соответствующую заглавной латинской букве D. Тем самым будет введена команда построения окружности , перпендикулярной трем заданным окружностям , и . Окружность останется выделенной. | |
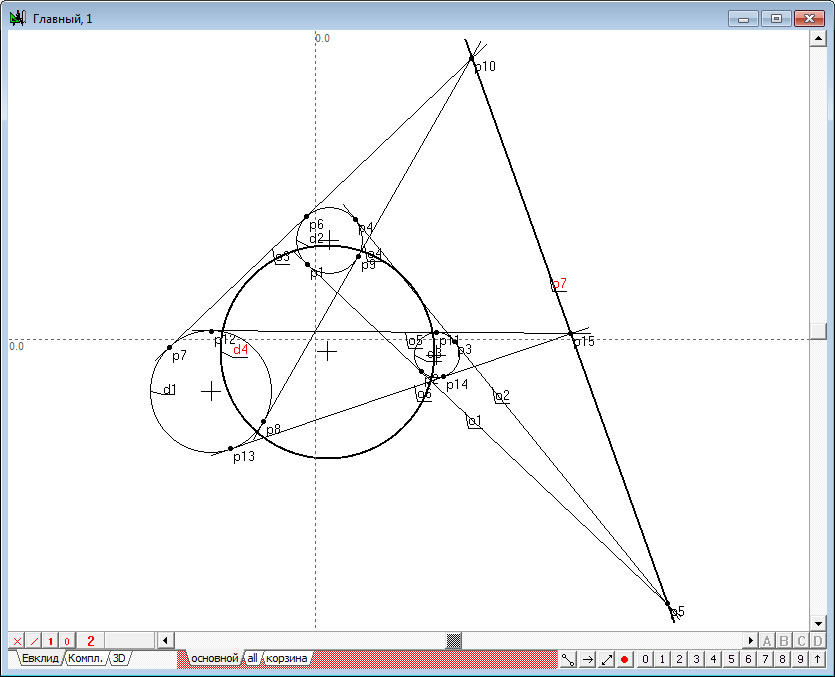
Рис. 3 |
||
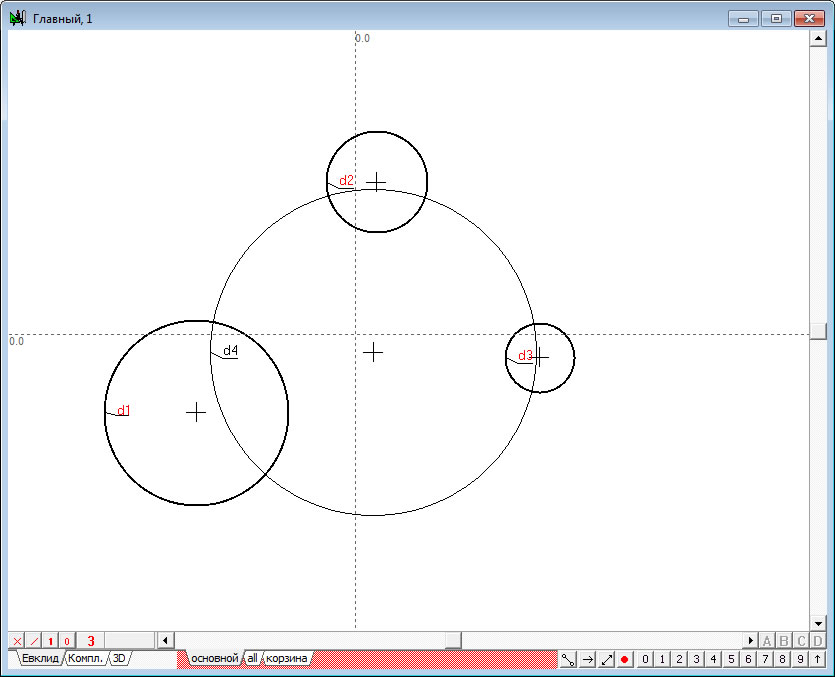
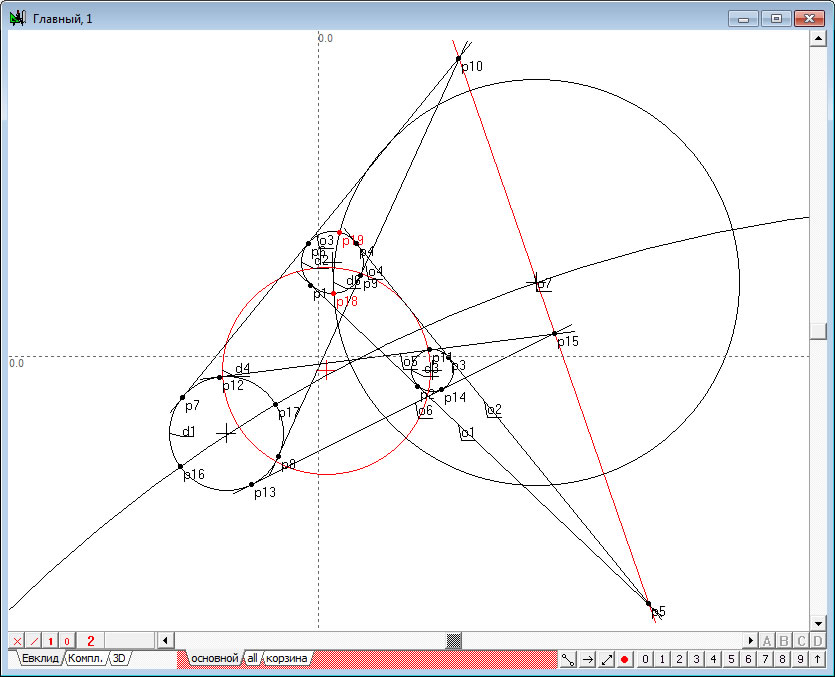
| 4. | Не снимая выделения с окружности (т.е. не выполняя никаких дополнительных щелчков мышью в области окна построения чертежа), нажмем на клавишу «Backspace», при этом восстановится выделение исходных окружностей , и . | |
Рис. 4 |
||
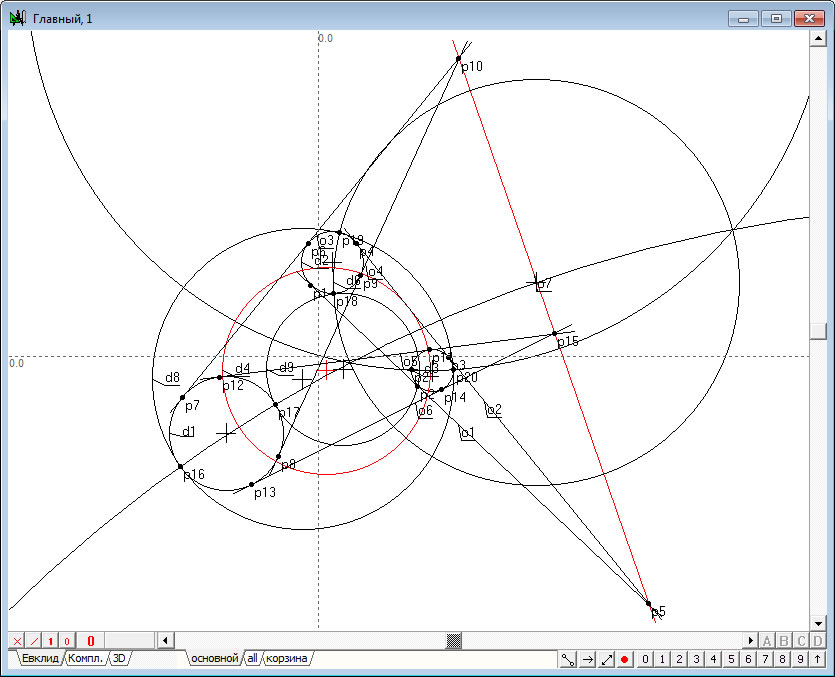
| 5. | Нажмем на клавиатуре латинскую букву o. В результате в программу будут добавлены сразу несколько функций, необходимых для построения центров подобия пар окружностей –, – и d2– окружностей и проведения через них прямой линии. Следует заметить, что все три центра подобия будут действительно лежать на одной прямой линии. | |
Рис. 5 |
||
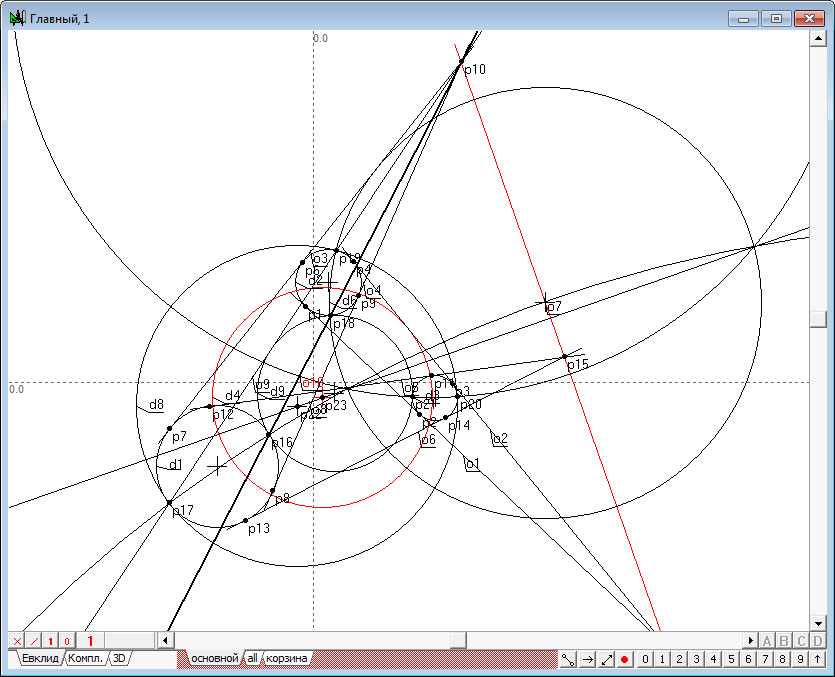
| 6. | Возможно, при выполнении последнего действия, часть сгенерированных объектов окажется за пределами области отображения окна, в котором формируется чертеж. Для того чтобы «втянуть» изображения всех объектов в область окна, следует нажать клавишу F4 | |
Рис. 6 |
||
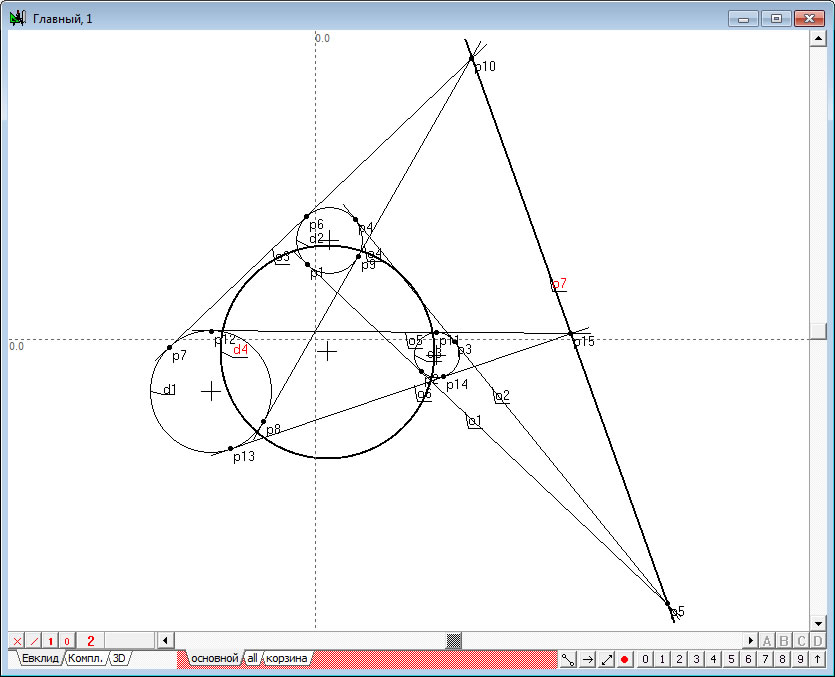
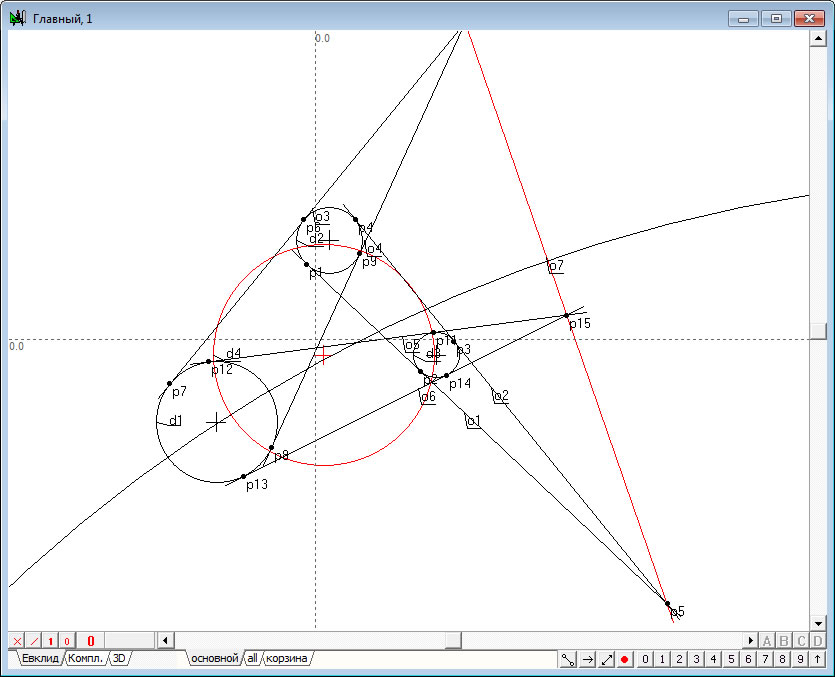
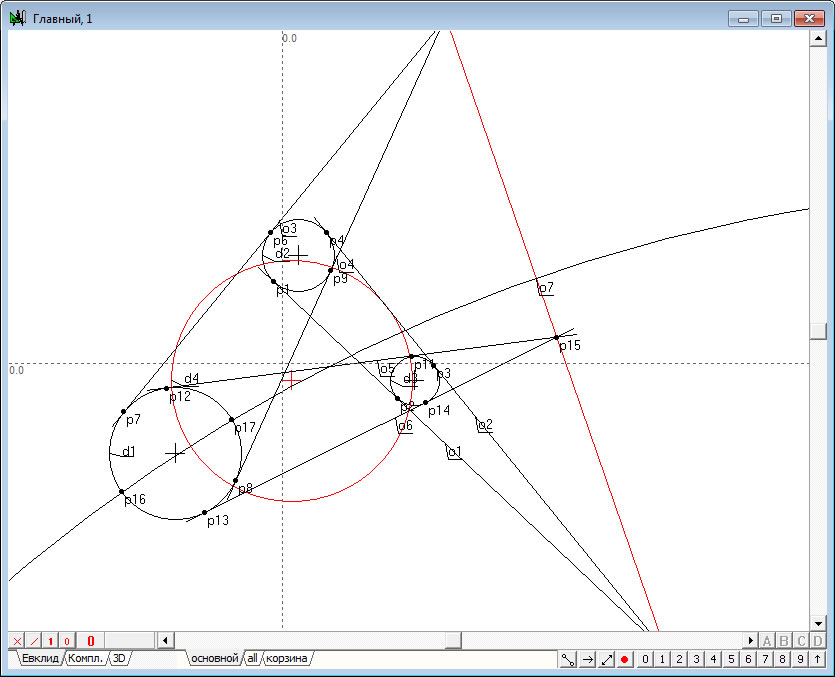
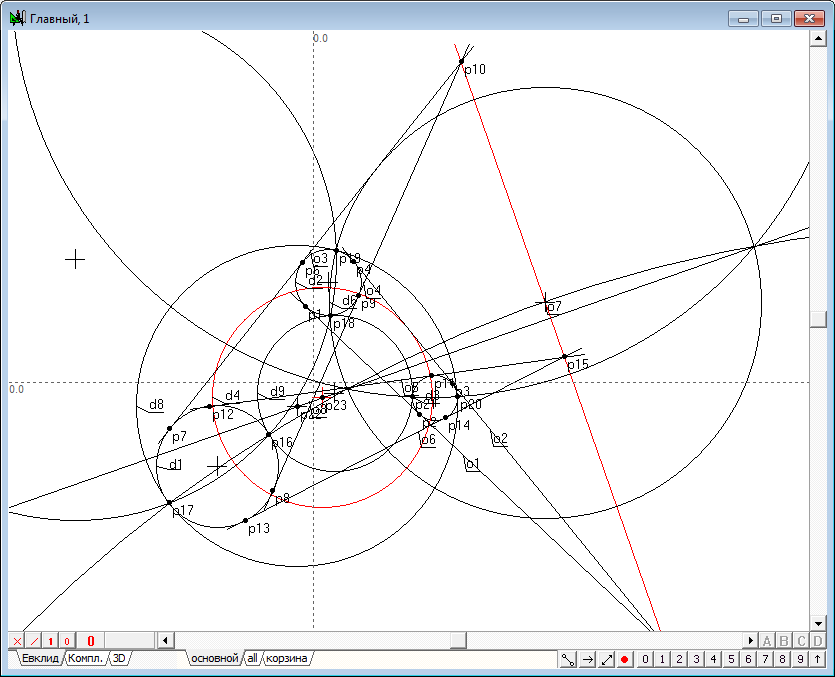
| 7. | Выделим теперь, удерживая нажатой клавишу Shift, прямую линию и окружность . | |
Рис. 7 |
||
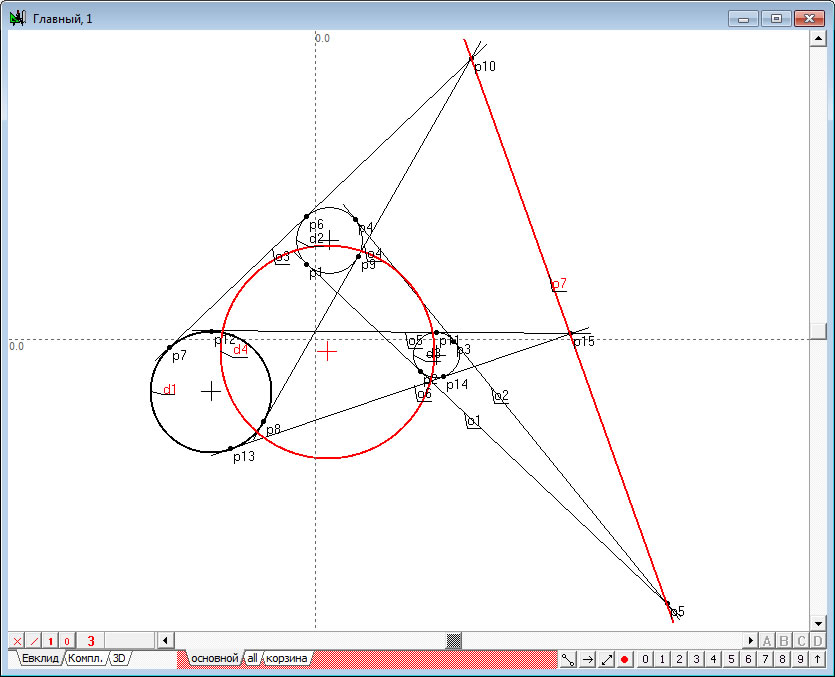
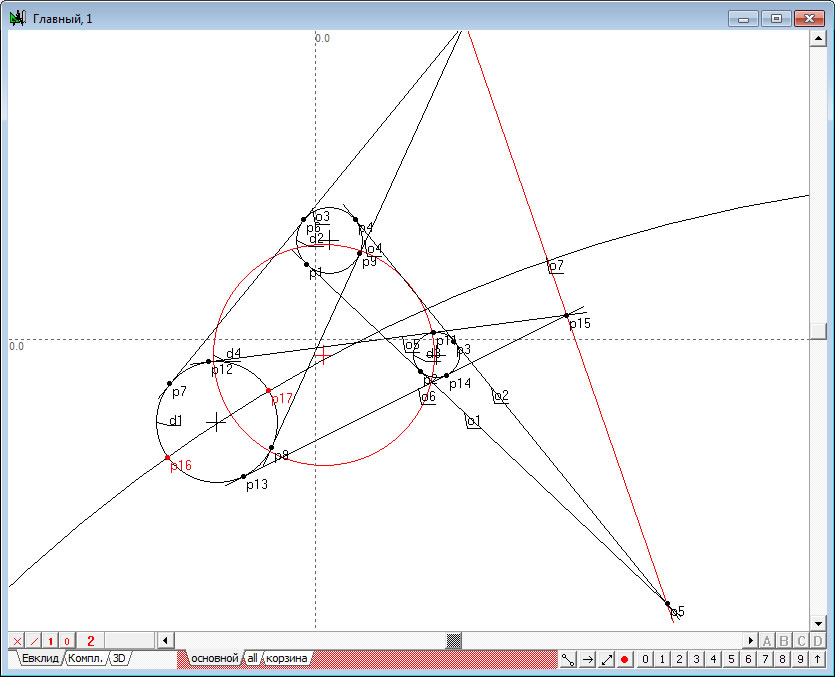
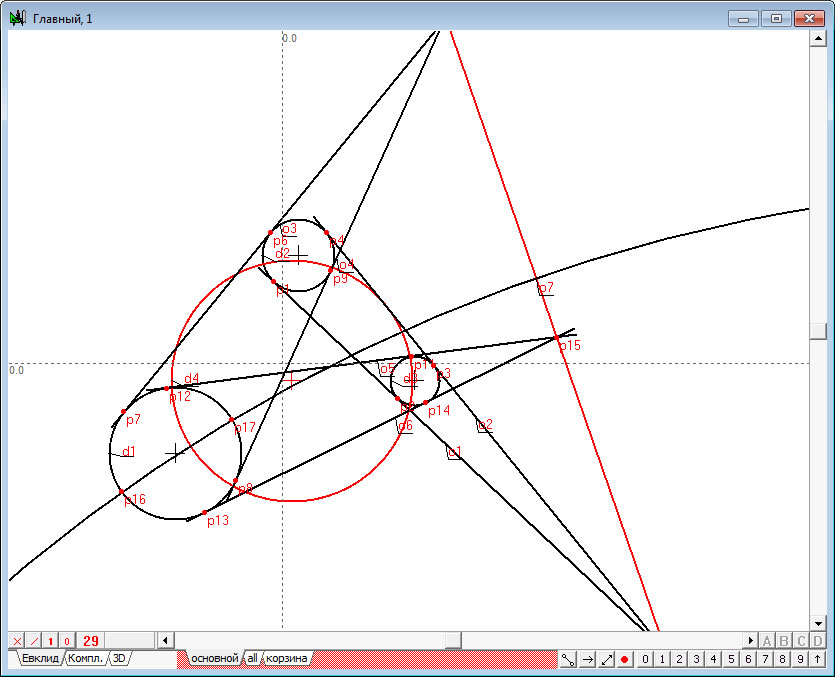
| 8. | Изменим цвет отображения этих объектов на красный. Для этого в палитре назначения атрибутов объекта необходимо раскрыть список цветов абриса и выбрать в нем пункт, отвечающий за назначение выделенным объектам признака красного цвета .
В процессе выполнения операции система запросит подтверждение, назначать ли выбранный атрибут всем выделенным объектам или же выполнить это назначение избирательно. На заданный системой вопрос рекомендуется ответить нажатием на кнопку «Ко всем».
|
|
Рис. 8 |
||
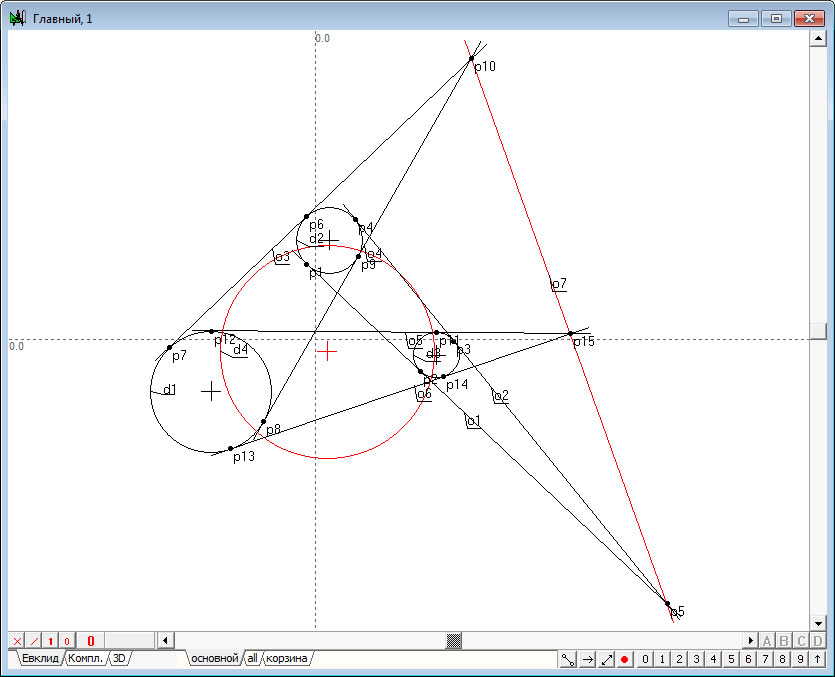
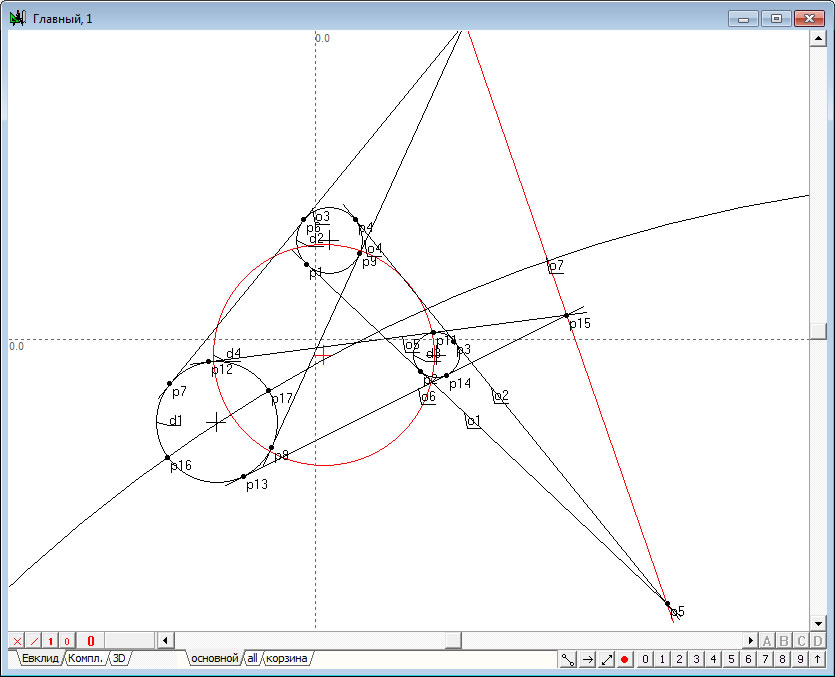
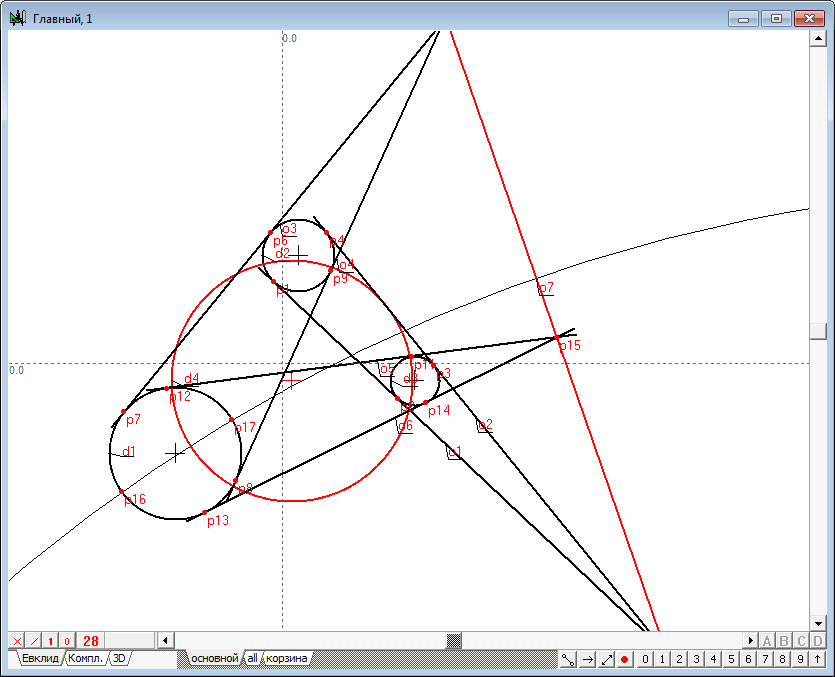
| 9. | Удерживая нажатой клавишу Shift, добавим к уже имеющемуся выделению окружность | |
Рис. 9 |
||
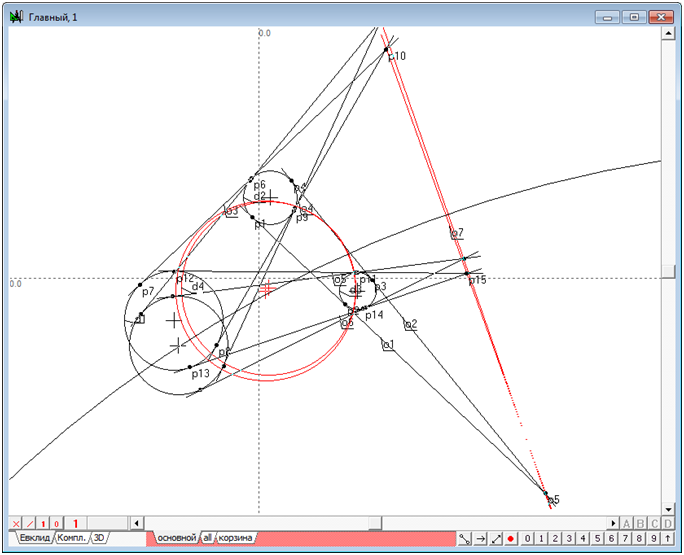
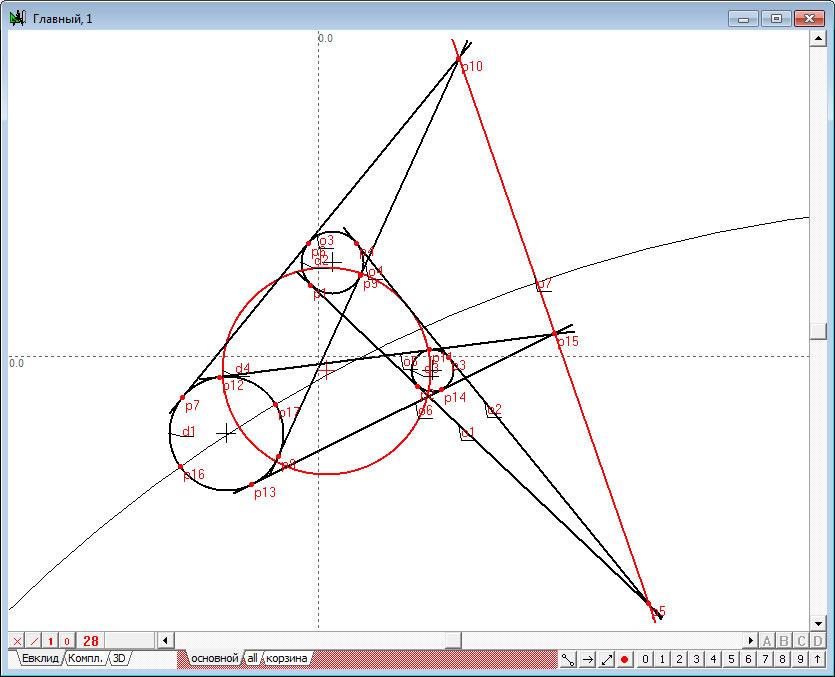
| 10. | Нажмем на клавиатуре клавишу с заглавной латинской буквой D. Вполне вероятно, что на экране не отобразится вновь построенная системой окружность d4.
Это может произойти из-за того, что радиус этой окружности оказывается очень большим и система не может ее отобразить в соответствии с общим для окружностей алгоритмом. Для того чтобы окружность отобразилась, переместим центр окружности
, например, вниз. Для этого выберем в палитре инструмент «шейпер» |
|
Рис. 10 |
||
Рис. 11 |
||
| 11. | После того как левая кнопка мыши будет отпущена, на экране зафиксируется следующий чертеж. | |
Рис. 12 |
||
| 12. | Удерживая нажатой кнопку Shift, добавим к выделенной окружности окружность и нажмем на клавиатуре клавишу с латинской буквой p. При этом в программу будет добавлена функция построения точек пересечения окружностей и с получением точек . | |
Рис. 13 |
||
| 13. | Снимем выделение со всех объектов, переведя курсор мыши в свободное от изображений геометрических объектов место, и выполнив над ним щелчок левой кнопкой мыши. Выделение с точек будет снято. | |
Рис. 14 |
||
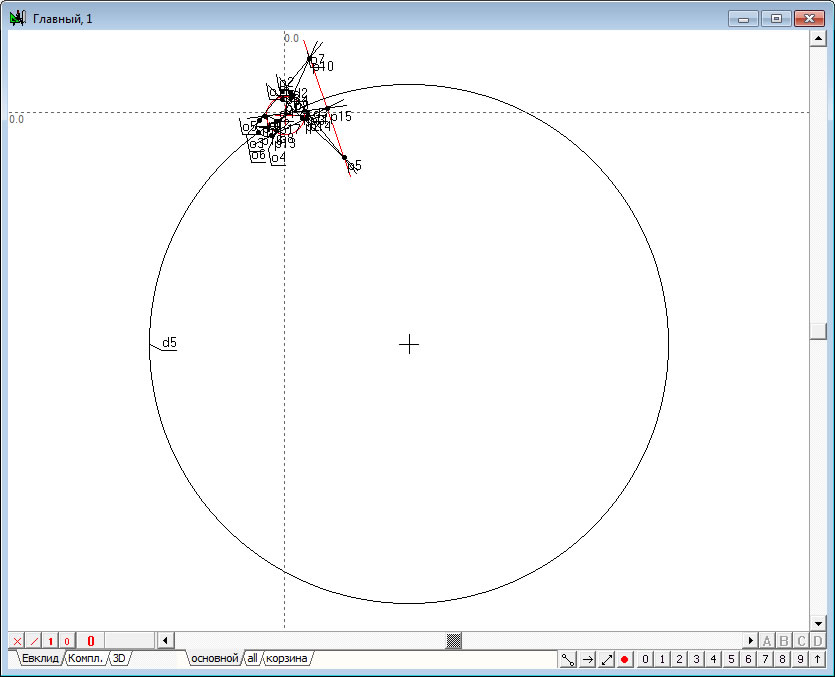
| 14. | В результате выполненных действий образовалась окружность , радиус которой по-прежнему остается довольно большим. Если сейчас нажать на клавиатуре кнопку F4, то это приведет к втягиванию в экран всего чертежа, в том числе и окружности , в результате чего большинство объектов геометрического построения станут малоразличимыми. | |
Рис. 15 |
||
| 15. | Для того чтобы вернуться к предшествующим характеристикам позиционирования и масштаба чертежа, следует нажать на клавиатуре комбинацию клавиш Alt+Z. | |
Рис. 16 |
||
| 16. | В то же время из чертежа видно, что некоторые точки, которые было бы желательно обозревать, остаются за пределами области отображения окна. Для того чтобы включить необходимые объекты в область отображения, можно применить следующий прием: 1. выделим все объекты построения комбинацией клавиш Ctrl+A. |
|
Рис. 17 |
||
| 17. | 2. Удерживая нажатой клавишу Shift, укажем курсором на изображение окружности и нажмем на левую кнопку мыши. Тем самым окружность будет исключена из выделения. | |
Рис. 18 |
||
| 18. | 3. Введем с клавиатуры комбинацию клавиш Shift+F4. Тем самым в экран будут «втянуты» изображения лишь тех объектов, которые остались выделенными. | |
Рис. 19 |
||
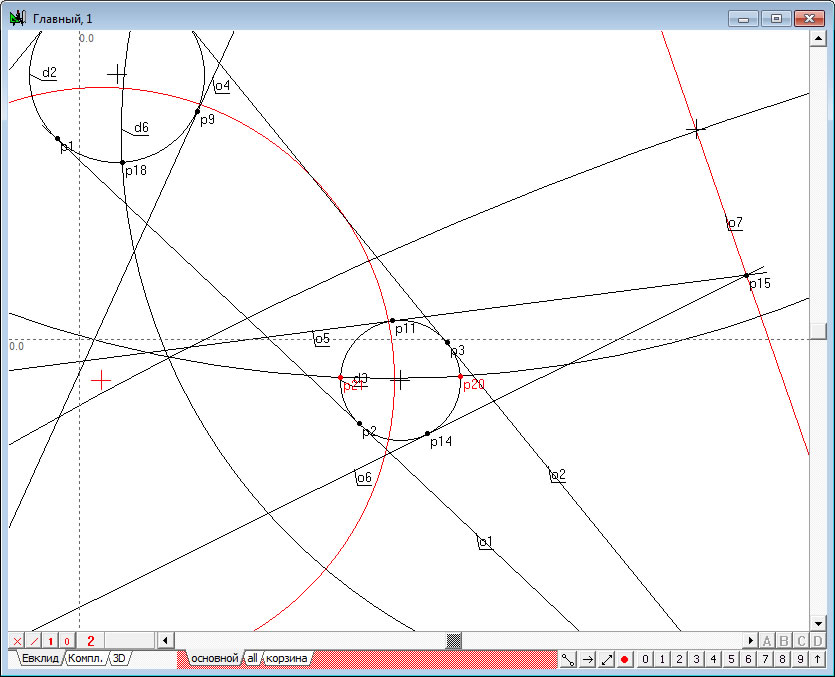
| 19. | Снова снимем выделение со всех объектов, щелкнув мышью над свободным от изображений геометрических объектов полем чертежа. | |
Рис. 20 |
||
| 20. | Теперь, удерживая нажатой клавишу Shift, выделим курсором выбора объекты и нажмем клавишу, соответствующую заглавной латинской букве D. Это позволит нам построить еще одну окружность , которая будет перпендикулярна к исходным выделенным объектам . | |
Рис. 21 |
||
| 21. | Удерживая нажатой клавишу Shift, добавим к выделению окружность и нажмем на клавиатуре клавишу p, чтобы получить точки пересечения этих окружностей . | |
Рис. 22 |
||
| 22. | Следуя той же логике построений, введем в программу окружность , перпендикулярную к объектам , и найдем точки пересечения окружностей . | |
Рис. 23 |
||
| 23. | Для построения окружностей, касательных к трем исходным окружностям, снимем выделение со всех объектов, а затем, удерживая нажатой клавишу Shift, выделим точки и нажмем на клавиатуре клавишу с латинской буквой g. В результате в программу будет введена функция построения окружности , проходящей через три заданные точки . Аналогичное действие следует выполнить и с точками , чтобы получить вторую касательную окружность | |
Рис. 24 |
||
| Пример |
||
| Теперь можно выполнить дополнительные исследования полученной модели. Рекомендуется испытать ее поведение, изменяя шейпером положения центров окружностей , а также их радиусов. Стоит обратить внимание на то, что центры окружностей находятся на прямой , а сами они пересекаются в двух общих точках. Интересно также то, что через эти точки можно провести прямую линию, причем центры сопрягающих окружностей и окружности также окажутся на этой линии. Эти свойства легко обнаружить и объяснить из полученного чертежа. Однако в этом же чертеже можно обнаружить множество других интересных свойств, если осуществить некоторые дополнительные построения. Выполним некоторые из них. | ||
| Соединим точки прямой линией , выделив эти точки, и нажав на клавиатуре клавишу o. Преобразуем полученный отрезок в бесконечную линию, изменив его атрибут нажатием на клавишу с символом ~. Убедимся в том, что построенная прямая пройдет через центр подобия окружностей - точку . Проведя прямую линию через точки обнаружим, что и она пройдет через точку . Аналогичные утверждения справедливы и в отношении других точек касания искомых окружностей к трем заданным окружностям (рекомендуется построить и проверить). | ||
Рис. 25 |
||
| Следующее интересное свойство заключается в том, что через пары полученных точек касания проходят окружности. Построим, например, окружность на точках , для чего выделим их и нажмем на клавишу с символом g, и убедимся, что полученная окружность пройдет и через точку . | ||
Рис. 26 |
||
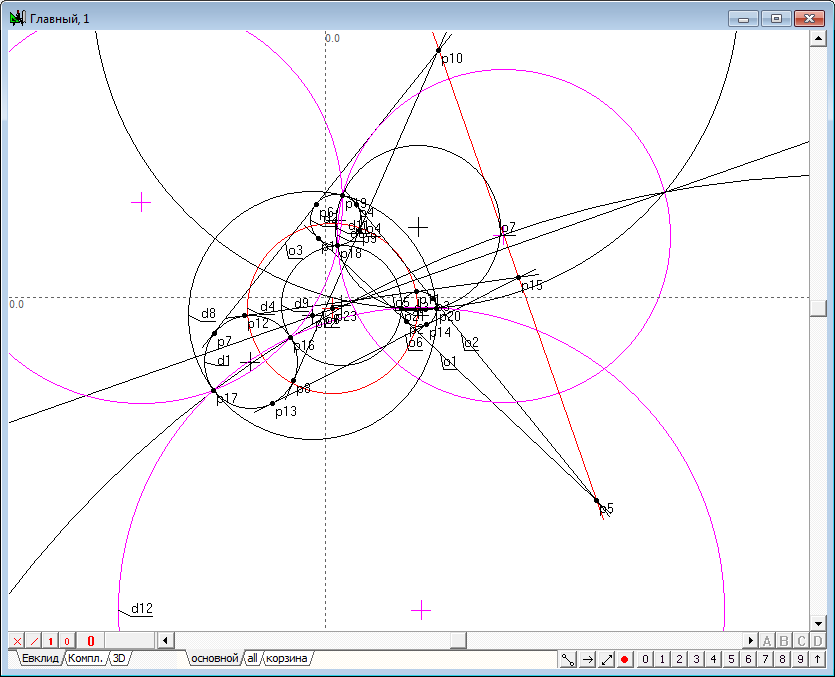
| Можно проверить, что аналогичное свойство проявляется в отношении точек и . Обратите внимание, как располагаются полученные и образованные построением окружности (пересекаются в общих точках) и где находятся центры этих окружностей. | ||
Рис. 27 |
||
Полученные результаты приводят к мысли о том, что решение задачи Аполлония в большой степени зависит от решения задачи нахождения точек пересечения двух окружностей и построения окружностей, перпендикулярных к заданным окружностям. Эта мысль побуждает к более подробному изучению этих базовых задач, тем более, что только что приведенный метод оказывается непригодным для решения задачи Аполлония, если, например, одна из исходных окружностей охватывает две другие окружности. Понятно, что в этом случае невозможно построить достаточное количество касательных прямых для того, чтобы получить ось подобия исходных окружностей. Однако это не означает, что в этом случае задача Аполлония не имеет решения - ее решение есть. Следовательно, нам необходимо более детально исследовать свойства геометрических объектов, которые определяют глубинную геометрическую суть решаемой задачи. Забегая вперед, хочется сказать, что такое изучение позволит нам вскрыть большое число неисследованных и, возможно, неизвестных ранее свойств, распространяя задачу Аполлония на области мнимых геометрических объектов, позволят перейти к аналогиям в многомерных пространствах, соединить эту задачу с геометрией треугольника и увидеть ее рекурсивную природу в нем. Следующая беседа будет посвящена проблемам пересечения окружностей и построения так называемых радикальных образов - прямых и точек, индуцированных парами и тройкам окружностей. Как мы вскоре увидим, радикальные образы, которые в геометрии определены для окружностей, можно достаточно просто связать с прямыми линиями и точками, что в свою очередь позволит сделать важные обобщения в отношении линейных и круговых объектов плоскости. |