|
||
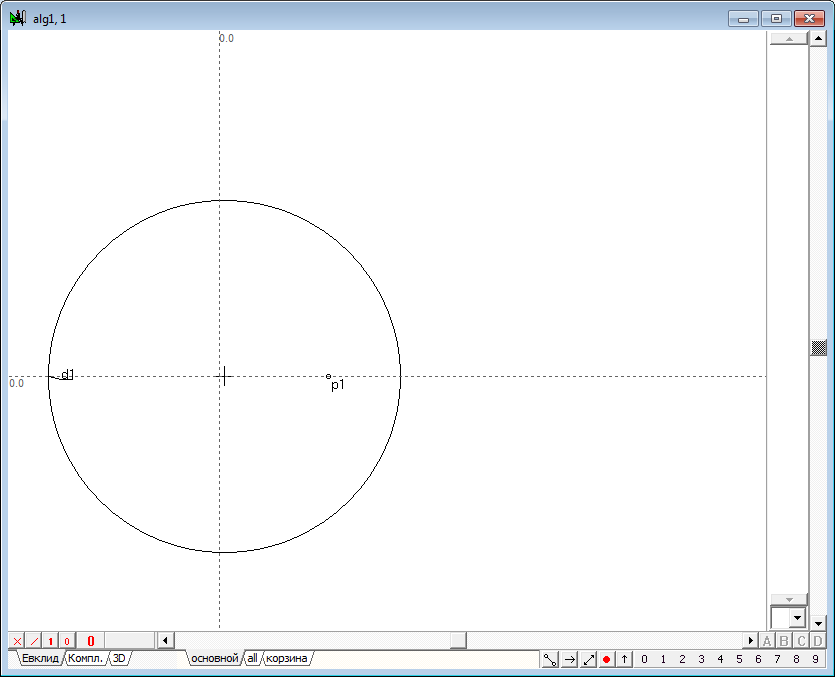
| 1 | Пусть заданы окружность инверсии d1 и точка p1, которую следует преобразовать в инверсии относительно окружности d1.
Рис. 1 |
|
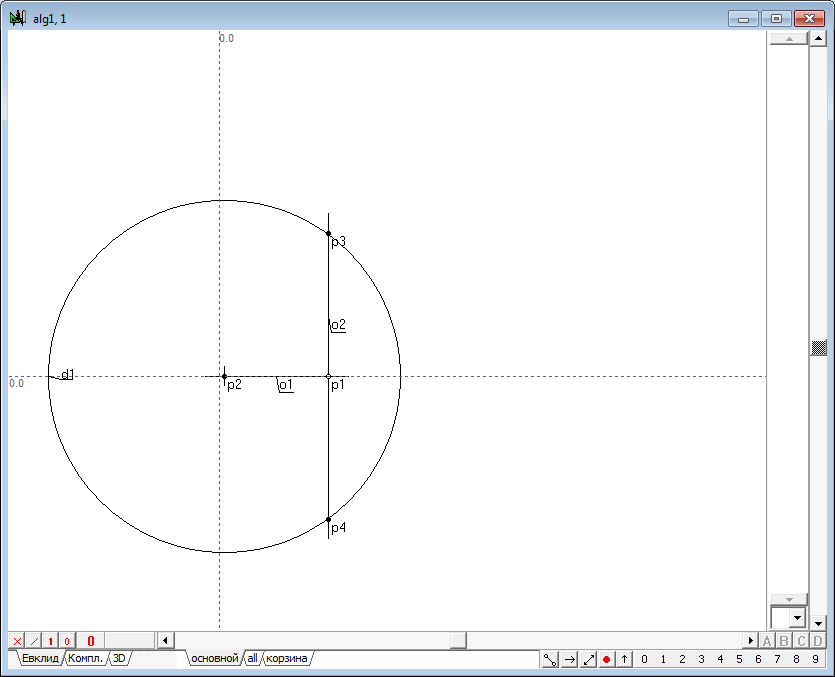
| 2 | Построим центр окружности инверсии - точку p2, проведем через p2 и p1 прямую линию o2, восстановим перпендикуляр к o2 в точке p1 и найдем точки пересечения прямой o2 с окружностью инверсии d1.
Рис. 2 |
|
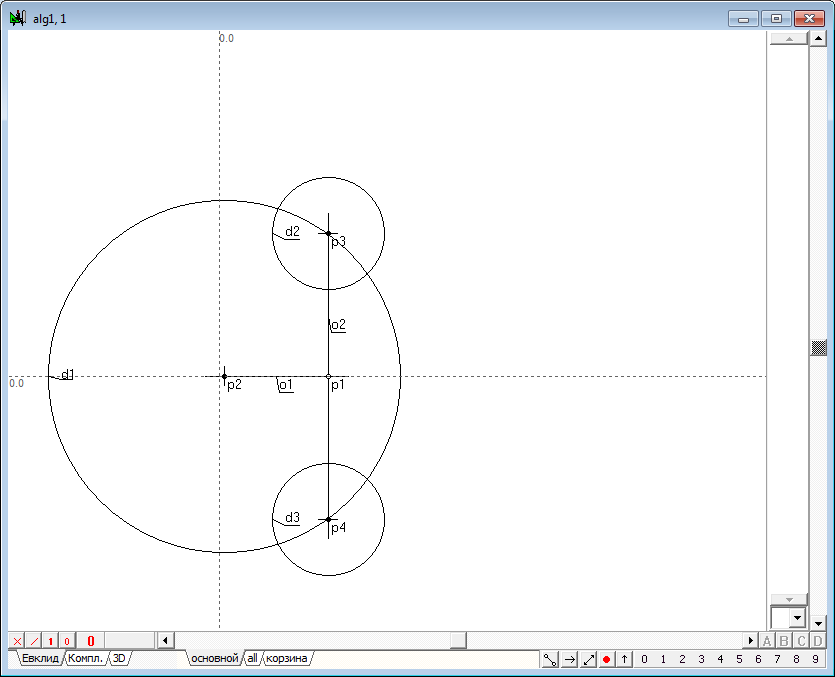
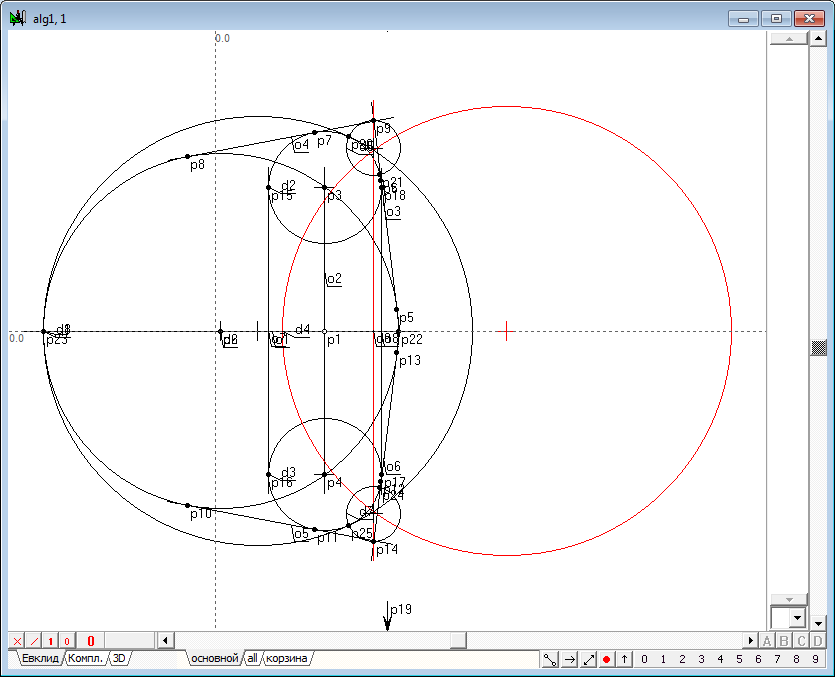
| 3 | Построим с центрами в точках p3 и p4 две окружности d2 и d3 одинакового произвольного радиуса.
Рис. 3 |
|
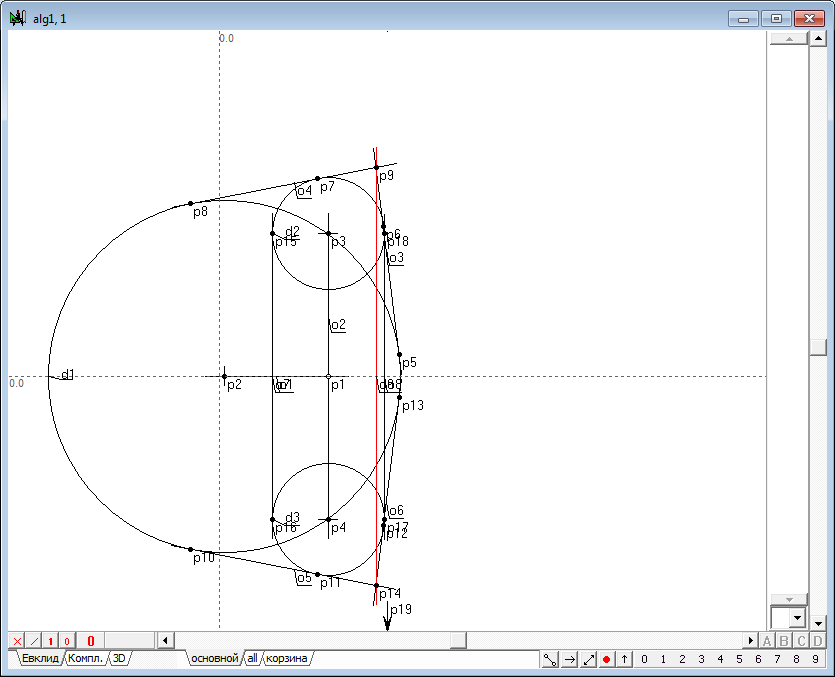
| 4 | Решим на основе полученной геометрической конструкции задачу Аполлония - найдем пару окружностей, касательных к трем окружностям d1, d2 и d3. Для этого найдем центр подобия p9 окружностей d1 и d2, центр подобия p14 окружностей d1 и d3 и несобственный центр подобия p19 окружностей d2 и d3.
Рис. 4 |
|
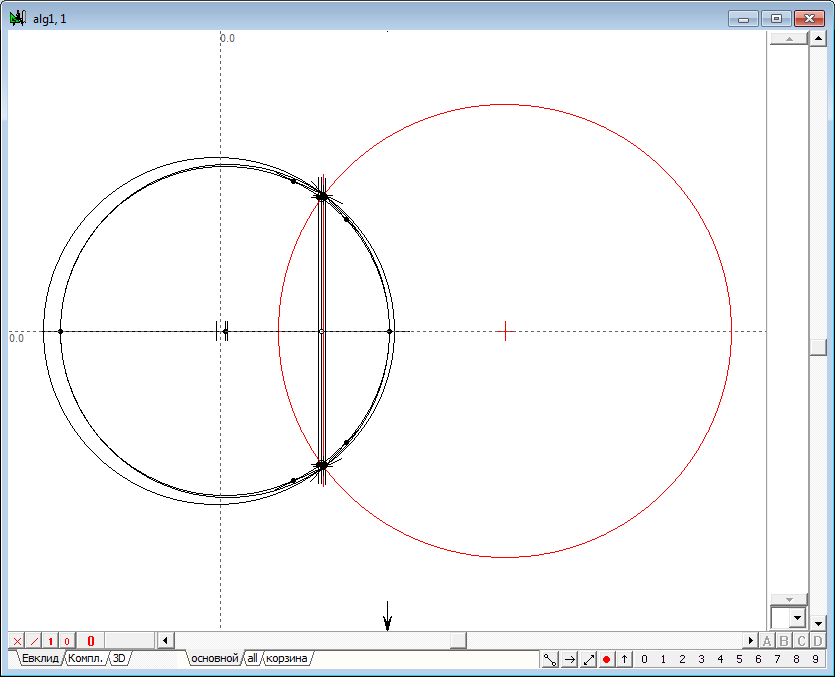
| 5 | Зная центры подобия p9, p14 и p19, проведем через них ось подобия o9 (выделена красным цветом).
Рис. 5 |
|
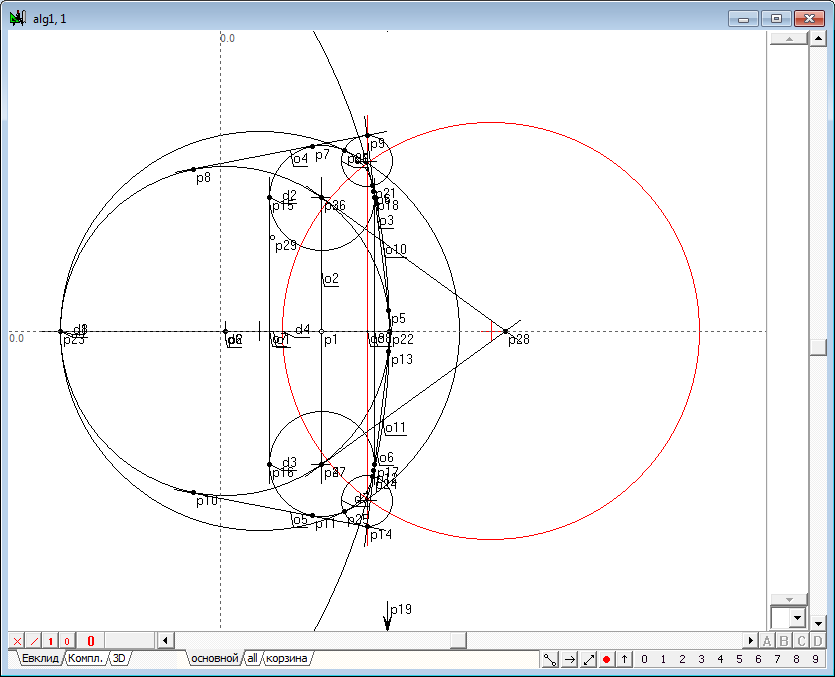
| 6 | Для нахождения точек касания искомых окружностей с окружностями d1, d2 и d3, проведем три окружности d6, d5 и d7, ортогональные к двум фиксированным объектам: прямой o9 и окружности d4 и к каждой из окружностей d1, d2 и d3.
Рис. 6 |
|
| 7 | Теперь, изменяя шейпером радиус окружности d2, устремляя его к нулю, можно наблюдать картину того, как искомые окружности d8 и d9 устремляются к окружности d1, а окружности d2 и d3 к точкам p3 и p4.
Рис. 7 |
|
| 8 | Завершим построение образа p28 точки p1 относительно окружности инверсии d1.
|
|
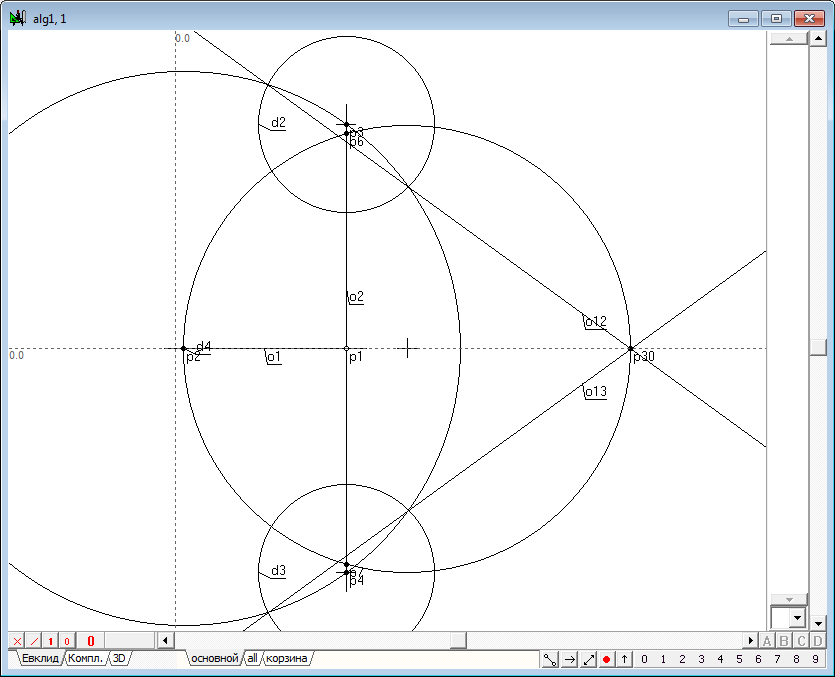
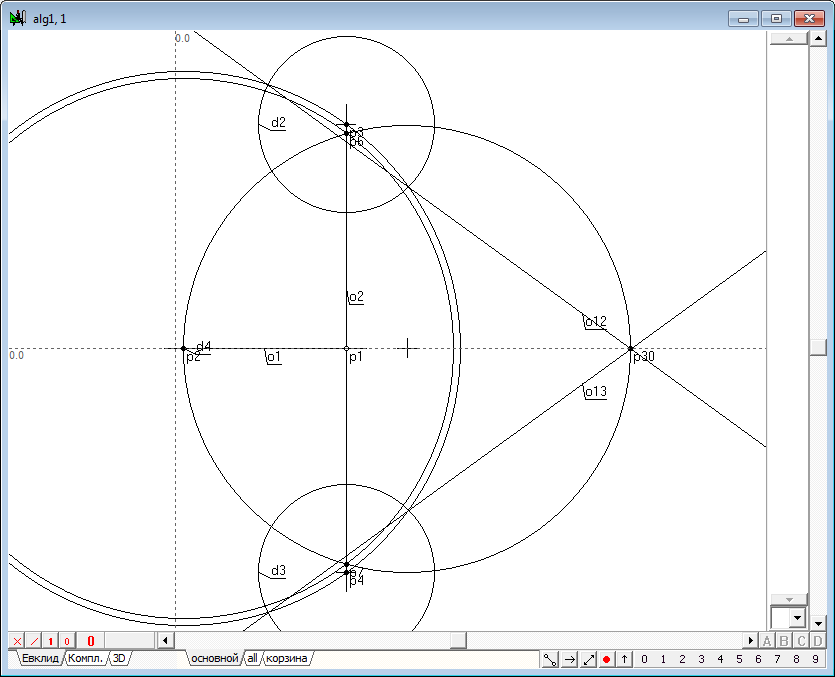
| 9 | Возникает вопрос, какая окружность инверсии, концентрическая с d1, переводит точку p1 в точку p20 и какова ее конструктивная взаимосвязь с окружностями d1, d2 и d3? Для ответа на этот вопрос уберем из чертежа объекты, не относящиеся к решаемой задаче. Для этого выделим точку p30 с предками, инвертируем выделение по отношениям и удалим полученное выделение комбинацией клавиш Shift+Delete.
Рис. 8 |
|
| 10 | Проведем окружность d5 через центр окружности d1 - p2 и точку p6. Окружность d5 является окружностью, переводящей в инверсии точку p1 в точку p30.
Рис. 9
|
|
| Пример |