|
||
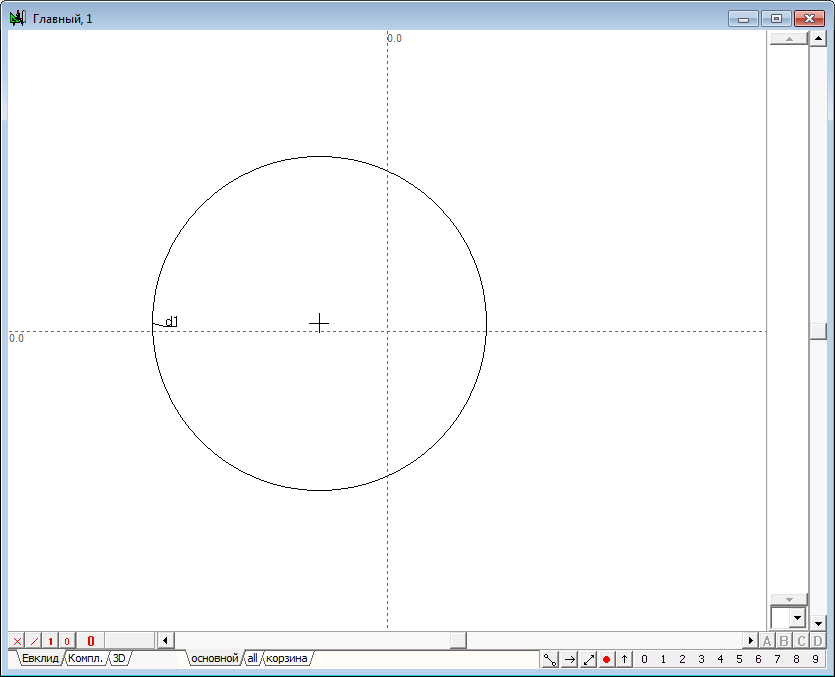
| 1 | Зададим на плоскости некоторую окружность d1, воспользовавшись, например, инструментом Свободная окружность.
Рис. 1 |
|
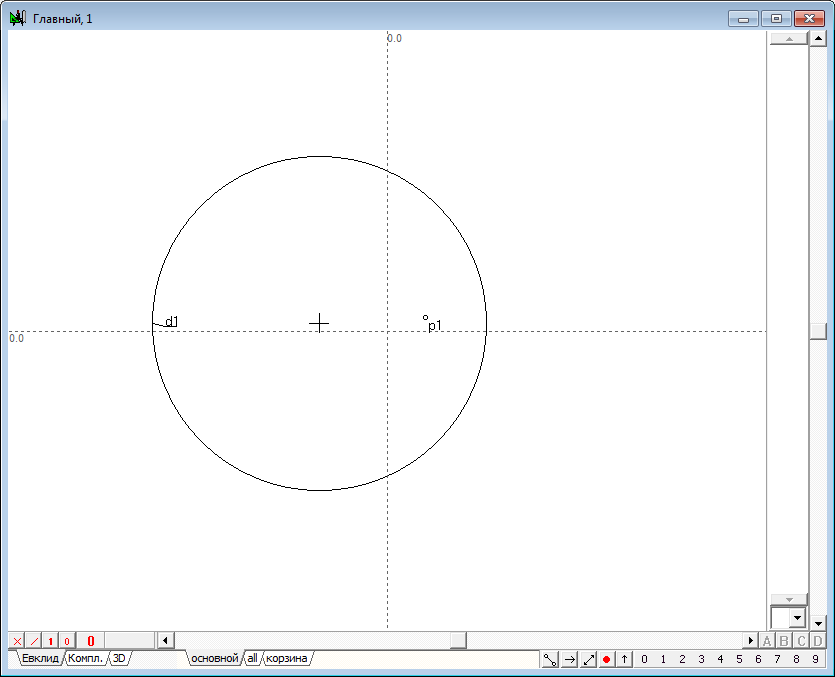
| 2 | Разместим во внутренней области окружности d1 точку p1, воспользовавшись инструментом Свободная точка.
Рис. 2 |
|
|
||
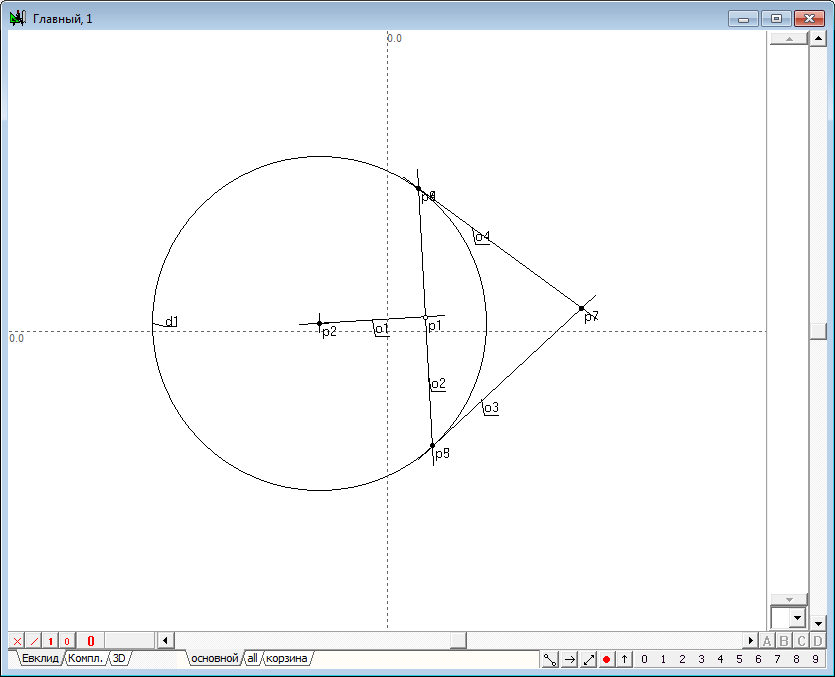
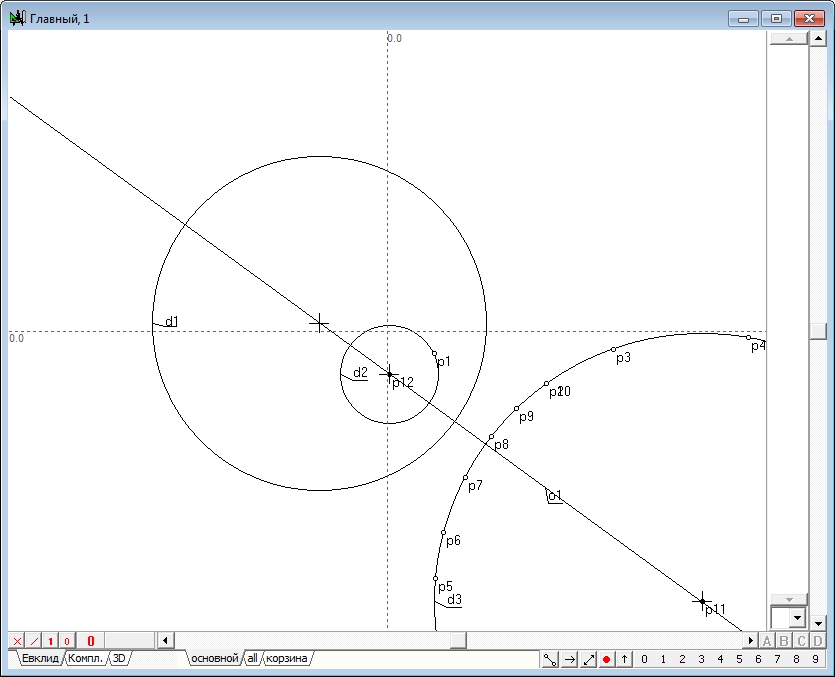
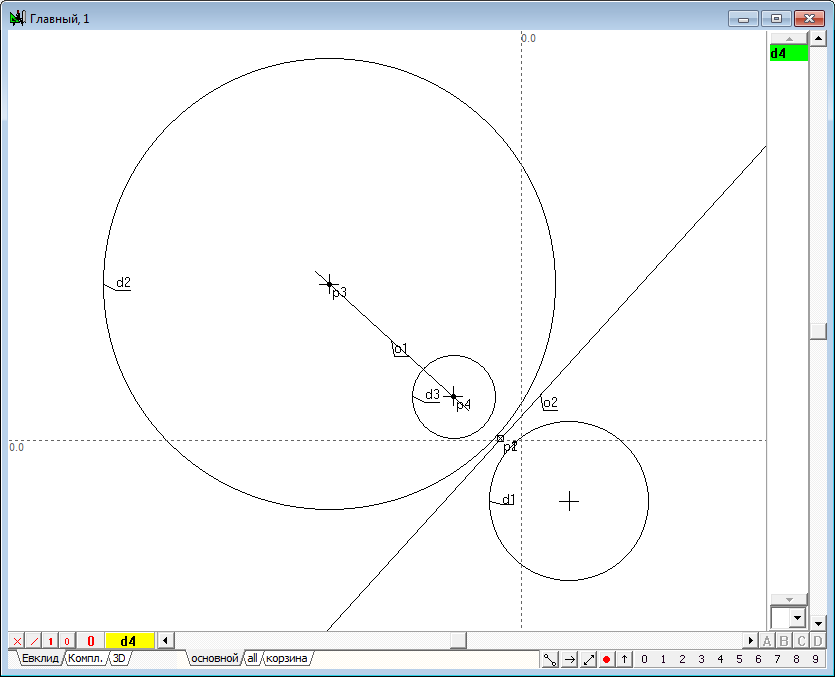
| 3 | Выполним теперь построение, которое будем называть нахождением образа точки в преобразовании инверсии, заключающееся в следующем: 1. Найдем центр p2 окружности d1, которую будем называть окружностью инверсии. Для этого выделим окружность d1 и нажмем на клавиатуре клавишу с латинским символом с. 2. Проведем через исходную точку p1 и центр p2 прямую линию o1, для сего выделим обе точки и нажмем на клавиатуре клавишу с латинским символом o, а затем клавишу с цифрой 8, для того чтобы изменить атрибут линии с ограниченного на инцидентностный. 3. Восстановим перпендикуляр o2 к линии o1 из точки p1, для чего, удерживая нажатой клавишу Shift, добавим к выделению (линии o1) точку p1 и нажмем на клавиатуре клавишу с латинским символом o. 4. Найдем точки пересечения линии o2 с окружностью инверсии d1 - точки p3 и p4. Для этого, удерживая нажатой клавишу Shift, добавим к выделению окружность d1, а затем нажмем на клавиатуре клавишу с латинским символом p. 5. Снимем выделение, отведя курсор на свободное от объектов место чертежа и щелкнув левой кнопкой мыши. Теперь построим последовательно две касательные к окружности d1, проходящие через точки p3 и p4. Для этого выделим окружность d1 и точку p3, а затем нажмем на клавиатуре клавишу с латинским символом o, в результате чего получим касательную o3. Сняв с нее выделение, вновь выделим окружность d1, но уже совместно с точкой p4, и построим касательную o4. 6. Найдем точку p7 пересечения касательных o3 и o4, для чего выделим их и нажмем на клавиатуре клавишу с латинским символом p.
Рис. 3 |
|
| 4 | Полученная точка p7 называется образом точки p1 в преобразовании инверсии, индуцированном окружностью d1. Воспользовавшись шейпером, выполним несколько перемещений точки p1 во внутренней области окружности d1. В результате наблюдений за динамикой построений, обнаружим, что точка p7 изменяет свое положение таким образом, что при перемещении точки p1 к окружности d1, точка p7 стремится занять положение, совпадающее с точкой p1, то есть расположиться на окружности. При перемещении точки p1 к центру окружности d1 - точке p2 , точка p7 стремится к бесконечности в направлении отрезка o1. В случае совпадения точки p1 с p2, геометрическое построение не может быть выполнено из-за неопределенности положения прямой o1. В этом случае точка p1 отображается на всю бесконечно удаленную прямую, однако созданный нами алгоритм не поддерживает такое преобразование. И, наконец, при выходе точки p1 за пределы внутренней области окружности, мы наблюдаем вырождение алгоритма ввиду того, что точки p3 и p4 пересечения прямой o2 и окружности d1 становятся мнимыми и обычными средствами нам не удается построить касательные o3 и o4, опущенные из них на окружность d1. Поэтому и нахождение точки p7 становится невозможным. Однако следует заметить, что преобразование точки p1 в точку p7 является взаимно однозначным. По этой причине можно считать, что точка p1 соответствует точке p7 в преобразовании инверсии относительно окружности d1, если представленные на чертеже построения выполнить в обратном порядке, то есть взять за исходную точку аналог точки p7, опустить из нее две касательные на окружность d1, определить точки касания, провести через них прямую и найти точку ее пересечения с прямой, проходящей через центр окружности инверсии d1. Преобразование в котором соответственные объекты переходят друг в друга называется инволюцией. Доопределив исходное построение обратным, получим полное преобразование инверсии, переводящим любую точку в ее образ, исключая лишь несколько случаев: 1. Исходная точка не должна совпадать с центром окружности инверсии; 2. Окружность инверсии должна иметь вещественный радиус, отличный от нулевого. |
|
| Поскольку преобразование инверсии является достаточно часто используемым в практике решения прикладных и исследовательских задач, рассмотренное нами геометрическое построение было положено в основу алгоритма работы одноименной функции Симплекса - Инверсия объекта. Поэтому нахождение образа точки в инверсии может быть найдено в результате выполнения одной операции без необходимости выполнения "прямого" и "обратного" построений, рассмотренных нами в целях знакомства с геометрической природой этого преобразования. Однако функция Инверсия объекта позволяет выполнять преобразования в инверсии не только точек, но и других геометрических образов, в частности, окружностей и прямых линий. Эти преобразования имеют ряд интересных свойств, с которыми мы познакомимся в результате выполнения следующих экспериментов. | ||
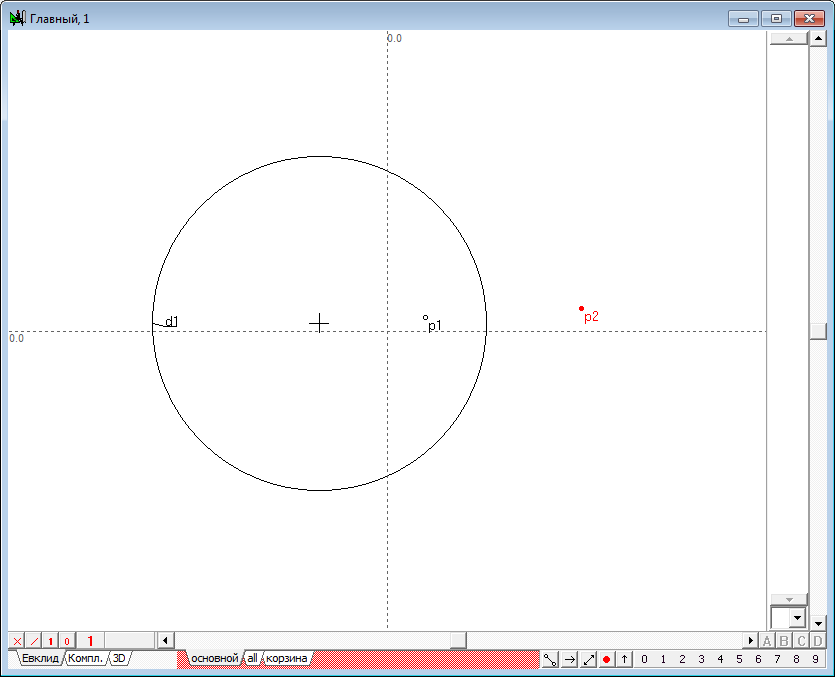
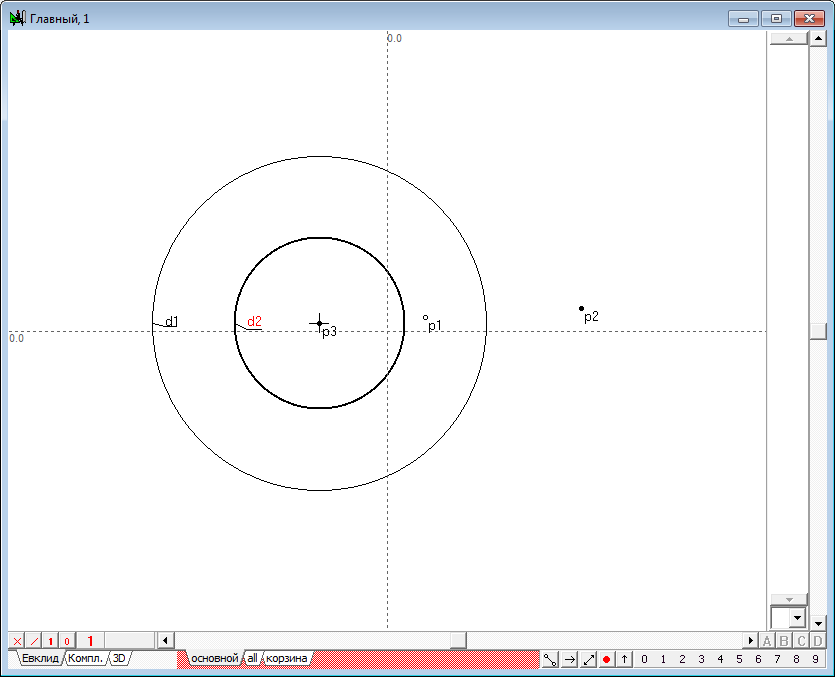
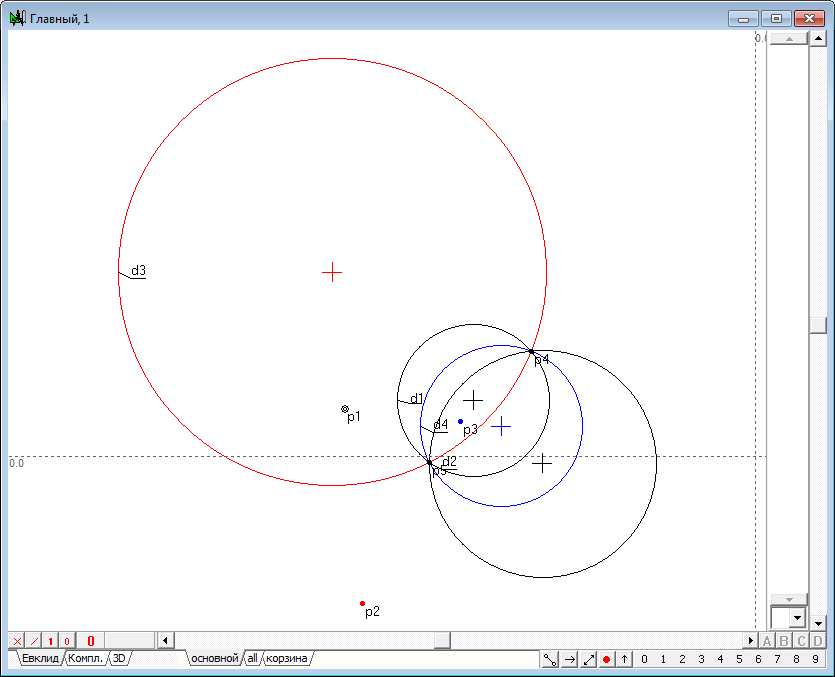
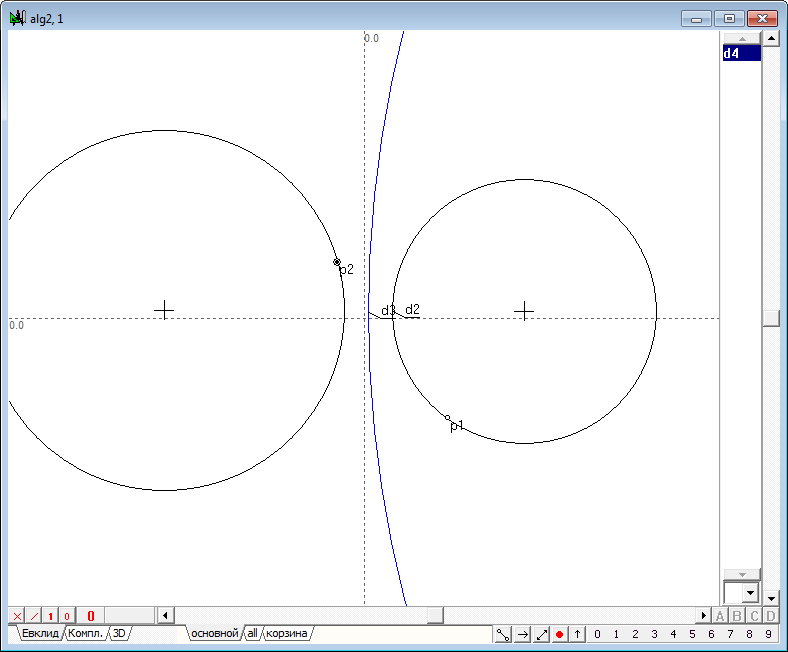
| 5 | Итак, начертим в поле чертежа некоторую окружность и разместим на чертеже точку p1, для которой мы будем искать образ p2 в преобразовании инверсии относительно окружности d1. Выполним это преобразование. Для этого выделим сначала точку p1, а затем, удерживая нажатой клавишу Shift, добавим к выделению окружность d1. Нажмем на клавиатуре клавишу с латинским символом i (нижний регистр). В результате выполнения команды будет построена точка p2. "Зацепив" точку p1 шейпером, начнем перемещать ее таким образом, чтобы ее траектория представляла бы собой окружность, концентрическую с окружностью d1. Нетрудно заметить, что точка p2 будет также перемещаться по траектории-окружности, концентрической с окружностью d1, из чего можно сделать вывод о том, что окружности, концентрические с окружностью инверсии, переходят в преобразовании инверсии в окружности, концентрические с исходной (и с самой окружностью инверсии). Разумеется, вручную перемещать точку таким образом, чтобы она строго соблюдала необходимые условия перемещения, достаточно сложно. Поэтому и результат преобразования можно оценить лишь качественно (с грубым приближением). Для того чтобы эксперимент дал более точные результаты, воспользуемся несколькими приемами, позволяющими задать точные перемещения точек на плоскости, а также зафиксировать результаты промежуточных построений.
Рис. 4 |
|
|
||
|
||
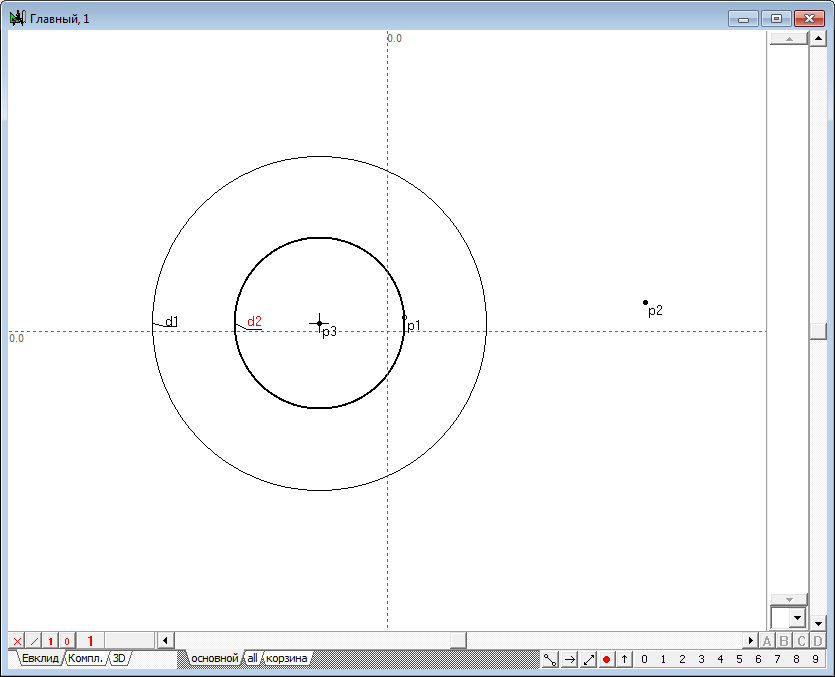
| 6 | Для того чтобы "заставить" точку p1 перемещаться строго по окружности, концентрической с окружностью d1, выполним следующие действия: 1. Найдем центр p3 окружности d1, выделив ее и нажав на клавиатуре клавишу с латинским символом c. 2. Отведем курсор на некоторое расстояние от выделенной точки p3 и нажмем на клавиатуре клавишу с латинским символом d. В результате будет построена концентрическая с окружностью d1 окружность d2.
Рис. 5 |
|
|
|
||
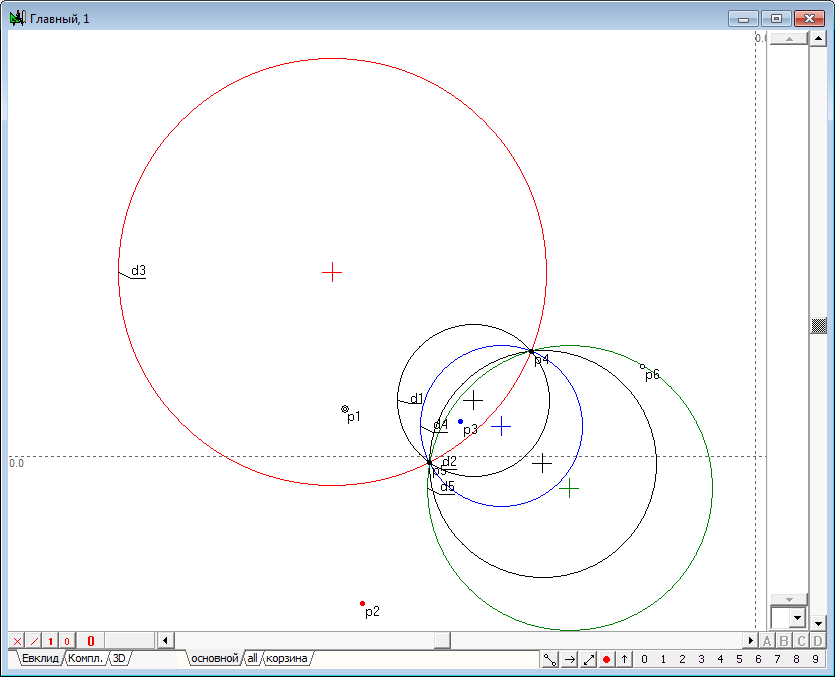
| 7 | "Зацепив" шейпером точку p1 и удерживая нажатой клавишу Shift, подведем точку p1 к окружности d2 так, чтобы она расположилась непосредственно над изображением ее очерка, после чего отпустим левую кнопку мыши, а затем и клавишу Shift. В результате выполнения этих действий функция, задающая точку p1 будет автоматически переопределена. С момента отпускания клавиши Shift точка будет задаваться функцией Точка принадлежит объекту. В частности, p1 теперь принадлежит окружности d2 с соответственным параметром положения, который был автоматически рассчитан в момент выполнения операции. Выполним перемещение точки p1 шейпером. Мы обнаружим, что точка p1 следует по окружности и не может занять произвольное положение на плоскости. В результате все зависящие от точки p1 объекты изменяют свое положение в соответствии с введенным на точку p1 позиционным ограничением, что позволяет исследовать "геометрическое поведение" точки p2 и наблюдать, как она перемещается по круглой траектории вслед за перемещением точки p1.
Рис. 6 |
|
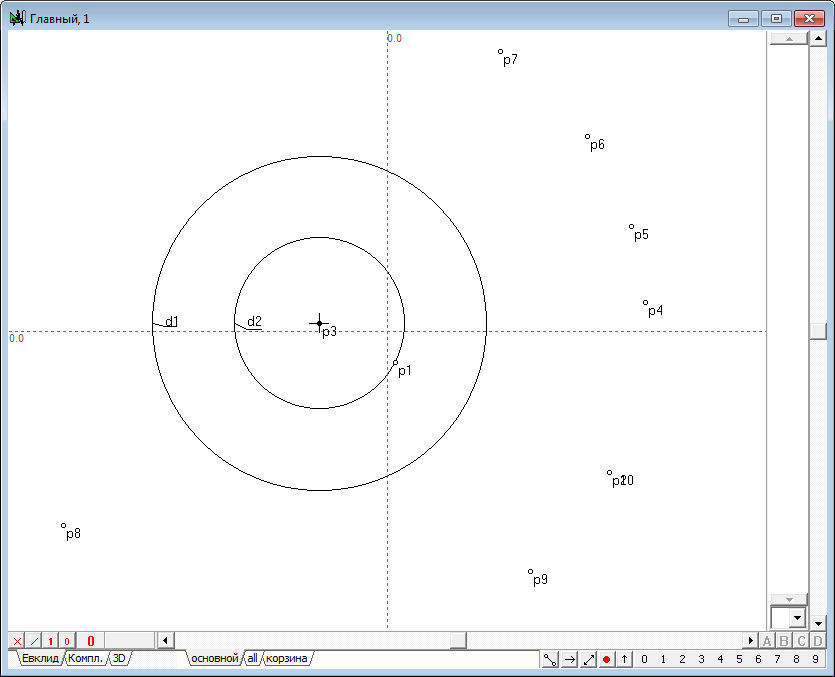
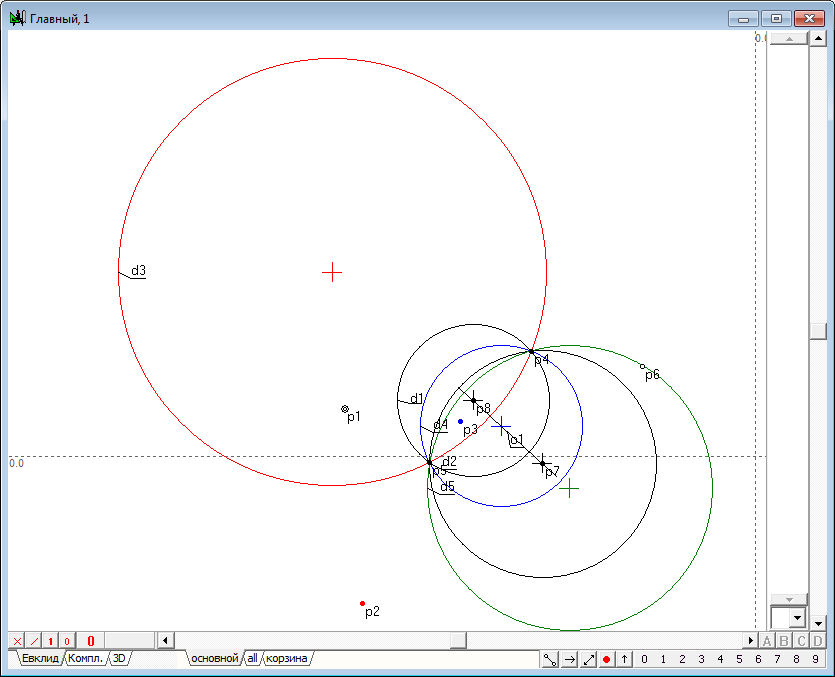
| 8 | Для того чтобы зафиксировать промежуточные положения точки p2, определяемые положением точки p1, можно воспользоваться следующим приемом: выделим точку p2, а затем в интересующем нас положении нажмем на клавишу с символом =. В результате этого действия в построение будет добавлена свободная точка с координатами, равными текущей координате выделенной точки. Многократное выполнение такого действия в различных положениях точки p1 позволит зафиксировать промежуточные положения точки p2, представленные набором дополнительных точек.
Рис. 7 |
|
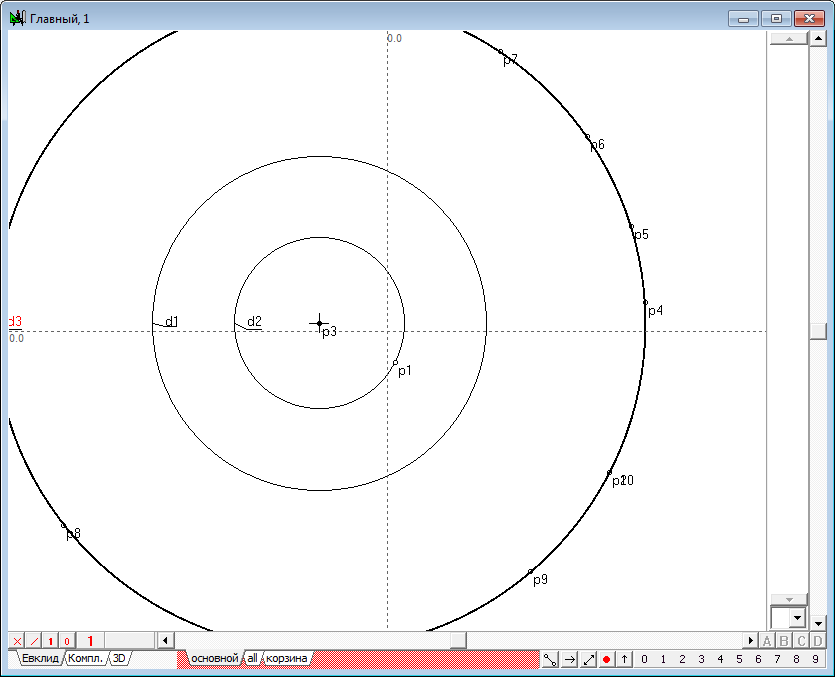
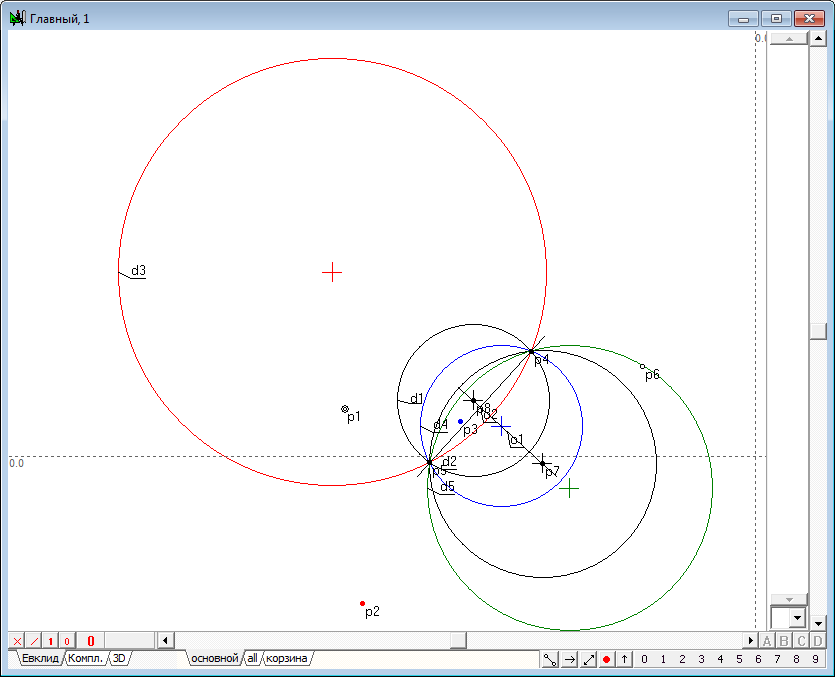
| 9 | Полученная картина позволяет визуально оценить характер преобразования, а при необходимости и удостовериться в его "подлинности". Так, например, выделив три точки p4, p5 и p6, проведем через них окружность, нажав на клавиатуре клавишу с латинским символом g.
Рис. 8 |
|
| 10 | Из чертежа отчетливо видно, что все остальные точки лежат на образованной окружности из чего можно сделать вывод (а точнее предположение) о том, что концентрические с окружностью инверсии окружности переходят в инверсии в концентрические окружности. Безусловно, следует понимать, что визуальная интерпретация не является строгим геометрическим доказательством наблюдаемых свойств. Для должного понимания сути происходящего необходимо выявлять строгие логические взаимосвязи, возникающие при взаимодействии объектов алгоритма. Однако достоинство предлагаемого "экспериментального" метода заключается в том, что визуальная интерпретация может подсказать путь к нахождению логического решения задачи и существенно повысить уверенность исследователя в правильности избранного пути. В дополнение к сказанному добавим, что точку p1 можно отсоединить от окружности d1 тем же способом, которым она присоединялась к ней. "Зацепим" точку p1 шейпером и нажмем клавишу Shift. После перемещения точки p1 на свободное поле чертежа и отпускания левой кнопки мыши и клавиши Shift точка p1 будет переопределена как свободная точка с координатами, соответствующими текущему положению курсора. |
|
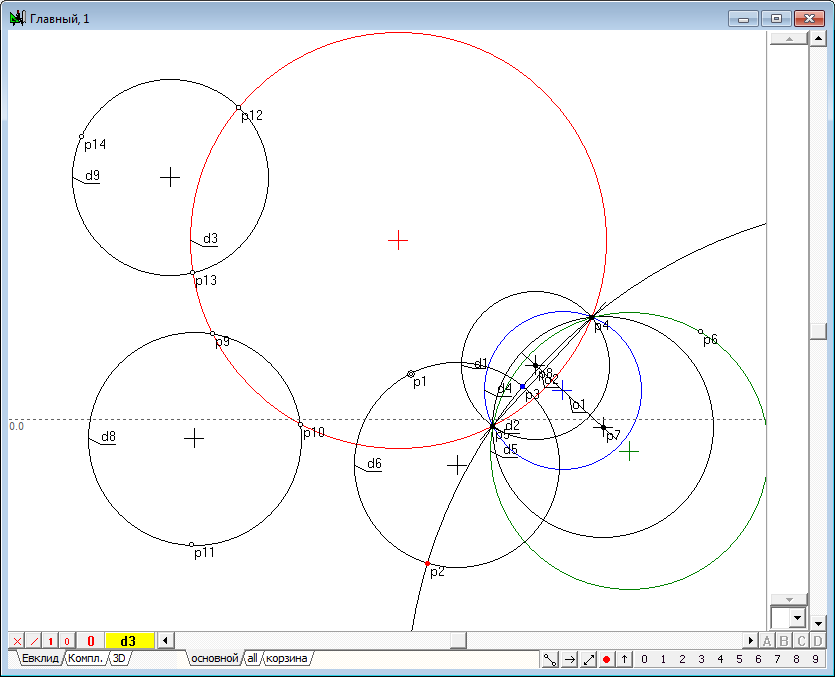
| 11 | Перейдем к исследованию преобразования окружностей в инверсии, не являющихся концентрическими с окружностью инверсии. Для этого начертим в поле чертежа некоторую окружность и поместим на нее точку, которую преобразуем в инверсии в ее образ. Действуя по схеме, намеченной в предыдущем примере, обнаружим, что окружность преобразуется в инверсии в другую окружность. Центры обеих окружностей находятся на прямой, проходящей через центр окружности инверсии.
Рис. 9 |
|
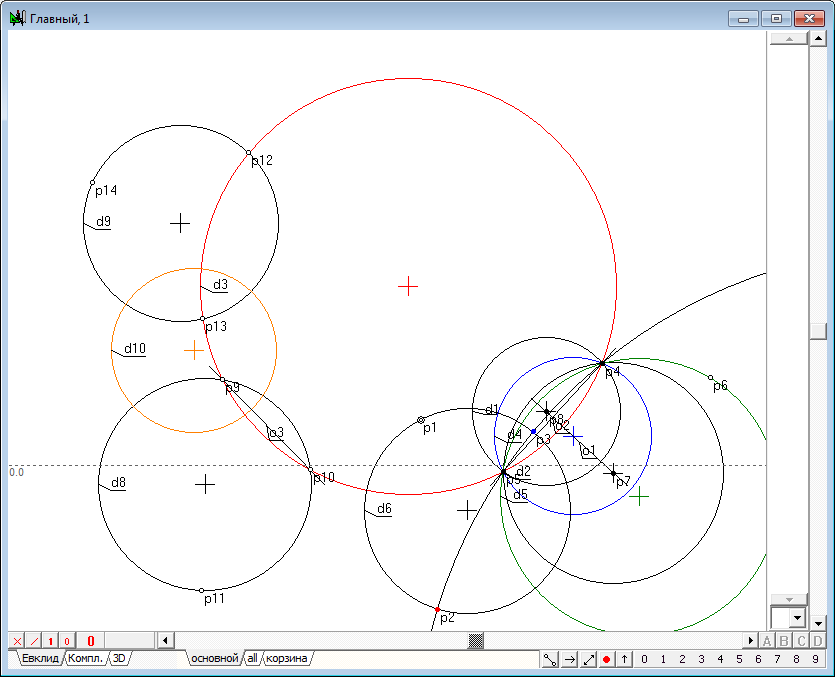
| 12 | Построим также радикальную ось o2 исходной окружности d2 и окружности-образа d3. Проведем окружность, ортогональную к окружностям d2, d3 и прямой o1, выделив эти объекты и нажав на клавиатуре клавишу с латинским символом D (верхний регистр). Из чертежа видно, что полученная окружность перпендикулярна также к окружности инверсии и к радикальной оси.
Рис. 10 |
|
| 13 | Наряду с преобразованием точек функция системы Симплекс Инверсия объекта позволяет осуществлять преобразование окружности относительно окружности инверсии. Так, например, несложно убедиться в том, что окружность d2, преобразуется в инверсии относительно окружности d1 в окружность d3. Равно как и окружность d3 преобразуется в инверсии относительно окружности d1 в окружность d2. Рассмотрим еще несколько замечательных свойств, относящихся к окружностям в преобразовании инверсии. Окружность, ортогональная по отношению к окружности инверсии преобразуется сама в себя. Равно как и окружность инверсии преобразуется относительно ортогональной окружности сама в себя, если последнюю рассматривать как самостоятельную окружность инверсии. Сказанное, однако, не относится к точечному ряду, расположенному на окружности. Так, например, если выполнить преобразование точки p8, инцидентной с окружностью d3, относительно ортогональной окружности, взятую за окружность инверсии, обнаружим, что ее образ будет инцидентен с окружностью d3, но не будет совпадать с точкой p8. И лишь точки пересечения обеих окружностей будут переходить сами в себя, являясь при этом двойными точками преобразования. |
|
| 14 | Пусть исходная окружность d1 и окружность инверсии d2 пересекаются явно в точках p1 и p2. Выполним преобразование инверсии окружности d1 относительно d2 с получением окружности d3.
Рис. 11 |
|
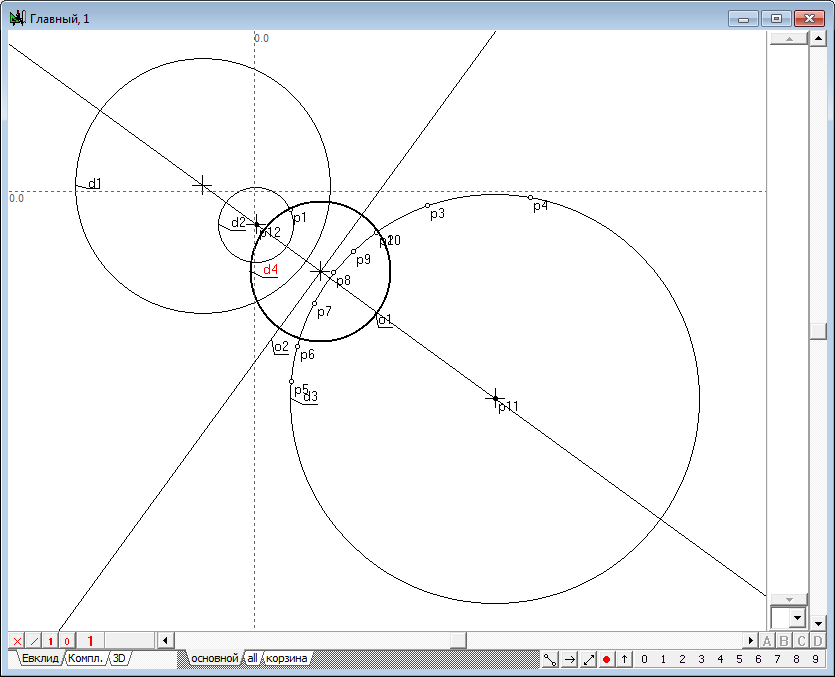
| 15 | Как видно из чертежа, все три построенные окружности проходят через точки p1 и p2 и, следовательно, являются представителями пучка окружностей, определенного двумя его центрами p1 и p2. Проведем еще одну окружность этого пучка, ортогональную к окружности инверсии d2. Для этого выделим точки p1, p2, окружность d2 и нажмем на клавиатуре клавишу с латинским символом D (верхний регистр). В результате этой операции образуется окружность d4. Являясь ортогональной к d2, окружность d4 в преобразовании инверсии переходит сама в себя. Обратим, внимание на еще одно замечательное свойство этой окружности. Так же, как и окружность d2, окружность d4, рассматриваемая как самостоятельная окружность инверсии, переводит окружности d1 и d3 друг в друга. Таким образом, можно утверждать, что для пары окружностей, проведенных на плоскости, существует пара ортогональных окружностей, переводящих исходные друг в друга в преобразованиях инверсии, определенной на каждой из окружностей ортогональной пары. Будем называть эти окружности инверсий сопряженными. Следует заметить, что такие окружности в общем случае переводят произвольную точку плоскости в две различные точки, между которыми, однако, обнаруживается определенная геометрическая зависимость. Поиском этой зависимости мы займемся при решении следующих далее задач. Все представленные на чертеже окружности являются представителями одного и того же пучка окружностей с центрами, являющимися точками пересечения двух исходных окружностей. Первой задачей, которую нам предстоит решить, будет задача отыскания двух окружностей, которые являются окружностями инверсии в отношении двух заданных окружностей включая и тот случай, когда исходные окружности не пересекаются явно (т.е. имеют мнимые точки пересечения).
Рис. 12 |
|
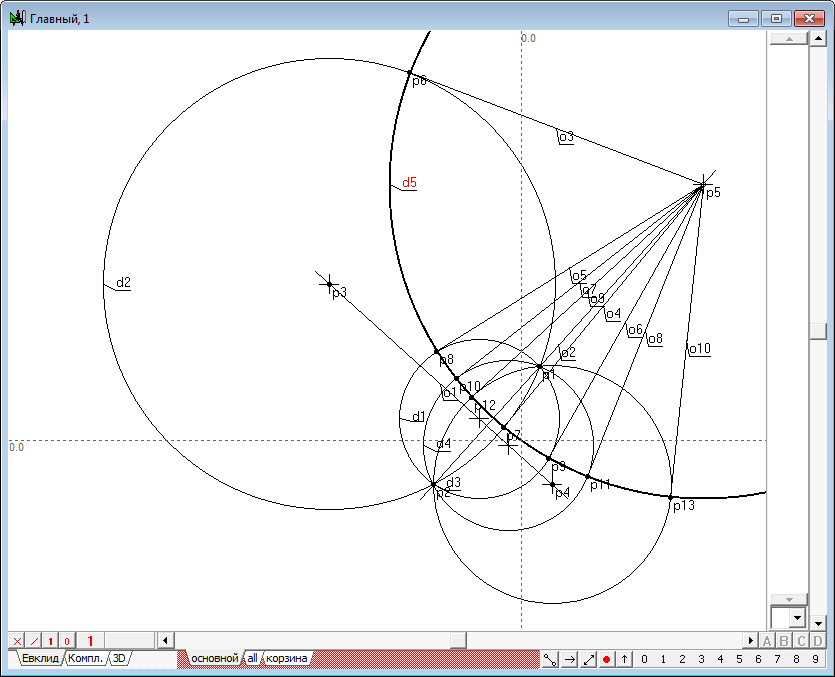
| 16 | Рассмотрим теперь такой вариант взаимного расположения исходной окружности и окружности инверсии, при котором исходная окружность проходит через центр окружности инверсии. Как уже было сказано выше, точка, совпадающая с центром окружности инверсии, отображается на любую из точек бесконечно удаленной прямой. Зная, что преобразование инверсии является взаимно однозначным за исключением рассмотренного случая, можно сделать вывод о том, что любые две несовпадающие точки, через которые проходит исходная окружность, преобразуются в инверсии в две несовпадающие точки. В то же время третья точка, совпадающая с центром окружности инверсии, должна неоднозначно перейти в бесконечность. Или, иными словами, эта точка должна быть однозначно сопоставлена с бесконечно удаленной прямой. Таким образом, нам потребуется дать ответ на вопрос: каким геометрическим образом будет представлен результат преобразования окружности, проходящей через центр окружности инверсии, если он должен будет пройти через две собственные точки плоскости и любую из бесконечно удаленных точек бесконечно удаленной прямой. Для ответа на этот вопрос проведем несложный геометрический эксперимент. Выберем на плоскости три несовпадающие свободные точки, проведем через них окружность (выделим три точки и нажмем на клавиатуре клавишу с латинским символом g). Две из них будем считать фиксированной, а третью начнем перемещать в бесконечность, причем по разным направлениям. Наблюдая за картиной происходящего, мы увидим, что вне зависимости от направления перемещения третьей точки к бесконечности окружность начинает "спрямляться". Из этого можно заключить, что вне зависимости от выбора направления на бесконечно удаленную точку образом исходной окружности в преобразовании инверсии будет прямая линия, проходящая через две фиксированные точки. Однако, учитывая, что единственной точке этой окружности соответствует бесконечно удаленная прямая следует признать, что к этому образу окружности добавляется в том числе и бесконечно удаленная прямая. Это добавление, которое обычно не учитывается, позволяет рассматривать полученную нами прямую-образ исходной окружности, как "полноценную окружность". Так, например, результатом пересечения прямой с окружностью являются две точки. Но, если бы произвольная (дополнительная) прямая линия пересекала бы прямую-образ без учета бесконечно удаленной прямой, то мы получили бы лишь одну точку. Если же бесконечно удаленная прямая принимается во внимание, то результатом пересечения произвольной прямой с нашим образом порождает две точки, что избавляет нас от исключений. При этом и в обратном преобразовании инверсии никаких исключений не образуется: две окружности будут пересекаться в двух точках, одна из которых совпадает с центром окружности инверсии, а другая будет соответствовать образу действительной точки, получившейся в результате пересечения дополнительной прямой и "собственной части" полученного нами первого образа. Все полученные на чертеже окружности, включая и обобщенный образ-прямую, обладают одной и той же радикальной осью, которая проходит через центры образованного пучка. Фактически, радикальная ось является ничем иным, как "собственной частью" образа окружности, проходящей через центры пучка окружностей и центр окружности инверсии. Отдельно заметим, что в паре объектов окружность-прямая (в обобщении до окружности) радикальной осью является сама прямая (вернее, ее собственная часть). Использованные в предыдущем абзаце оговорки требуют дополнительных разъяснений. Итак, согласно одному из свойств радикальной оси, касательные, опущенные из любой точки, инцидентной с этой прямой на любые окружности пучка, имеют одинаковую длину. Поэтому такая точка является центром окружности с радиусом, равным длине касательной, опущенной на любую из окружностей пучка, причем эта окружность будет ортогональной ко всем без исключения окружностям данного пучка.
Рис. 13
Рис. 14 |
|
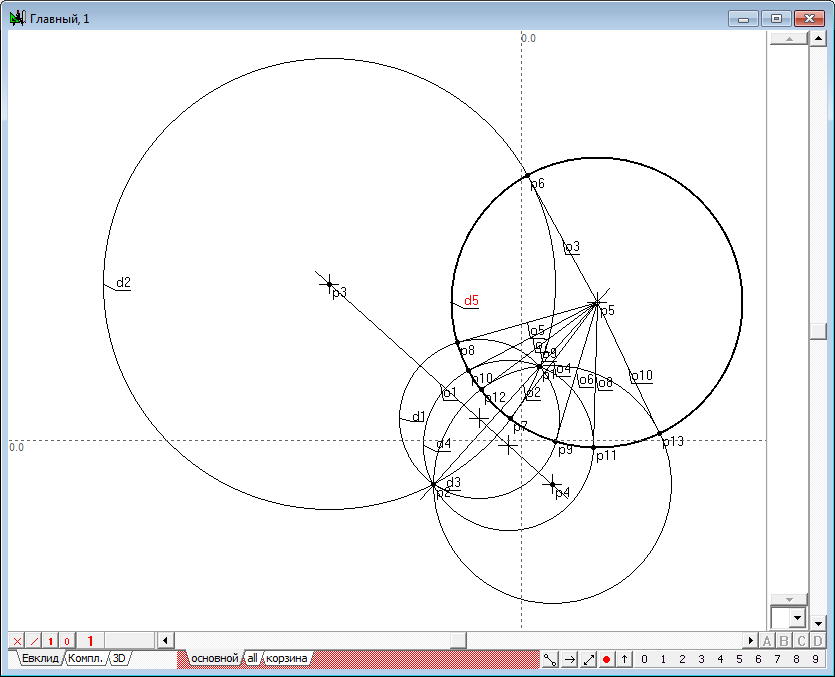
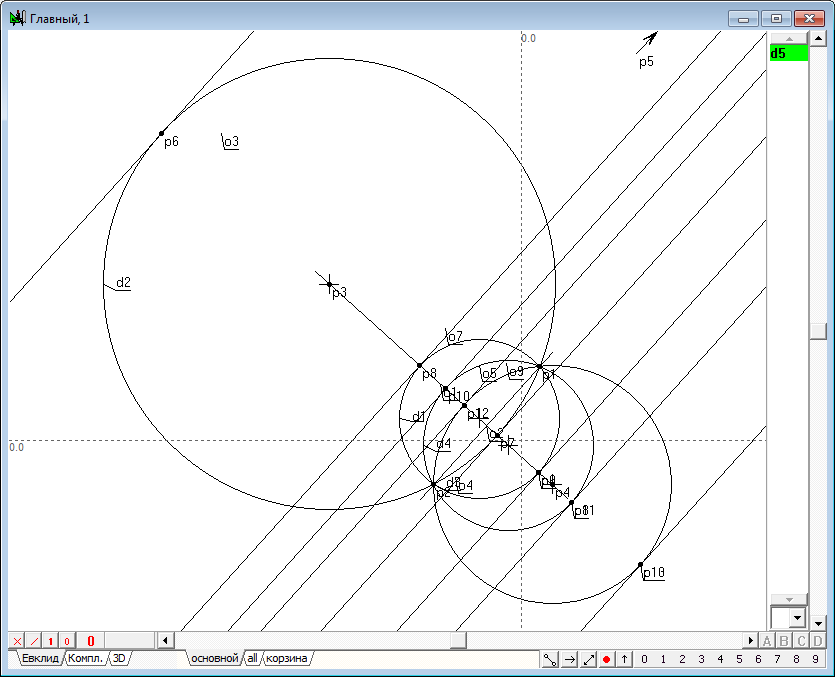
| 17 | Начнем перемещать точку p5 в бесконечность по направлению прямой o2. В процессе этого перемещения мы будем наблюдать посредством изменения окружности d5 присутствие еще одного пучка окружностей, ортогонального к исходному пучку. Доведя точку p5 до бесконечности в направлении прямой o2, опустим из p5 касательные на окружности исходного пучка. Такие касательные образуют пучок с несобственным центром - пучок параллельных прямых. Точки касания этих прямых с окружностями пучка будут располагаться на прямой o1 (являющейся окружностью в том же смысле, что и образ-прямая, рассмотренная в предыдущем примере), проходящей через центры этих окружностей, и эта прямая будет ортогональной по отношению к окружностям исходного пучка.
Рис. 15 |
|
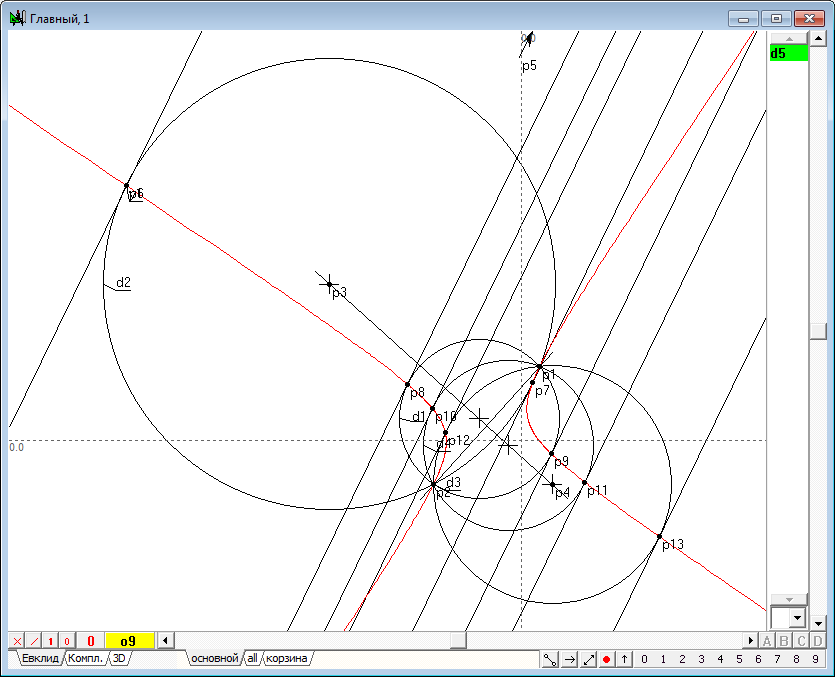
| 18 | Посмотрим, как изменится картина, если задавать точке p5 иное направление, не совпадающее с направлением прямой o2, перемещая ее по бесконечно удаленной прямой. Теперь мы уже не сможем построить ни прямую и ни окружность, которые проходили бы через точки касания пучка прямых к соответственным окружностям исходного пучка окружностей. Однако несложно заметить, что в данном случае через точки касания пройдет кривая второго порядка (гипербола y1 на чертеже). Поэтому следует заключить, что свойство радикальной оси нести на себе центры окружностей пучка, ортогонального к заданному, проявляется лишь на той части окружности, "выродившейся" в прямую, которая является ее "собственной" частью, вследствие чего радикальная ось должна рассматриваться как прямая линия, а не вырожденная окружность.
Рис. 16 |
|
| 19 | В том случае, если исходные окружности не пересекаются явно (то есть имеют мнимые точки пересечения), все представленные выше рассуждения должны оставаться в силе. Однако, в этом случае одна из окружностей инверсии становится мнимой и ее образ нельзя представить на чертеже непосредственно, становится невозможным "опереться" на ее очерк инструментально. Тем не менее, методы геометрического моделирования позволяют неявно использовать этот объект. Эта возможность основана на том, что мнимая окружность так или иначе задана на чертеже косвенно имеющимися в нашем распоряжении явными объектами и находится в геометрической взаимосвязи с ними. Следующая задача будет заключаться в том, чтобы построить общий алгоритм нахождения образа точки в инверсии относительно окружности любой природы - действительной или мнимой.
Рис. 17 |
|
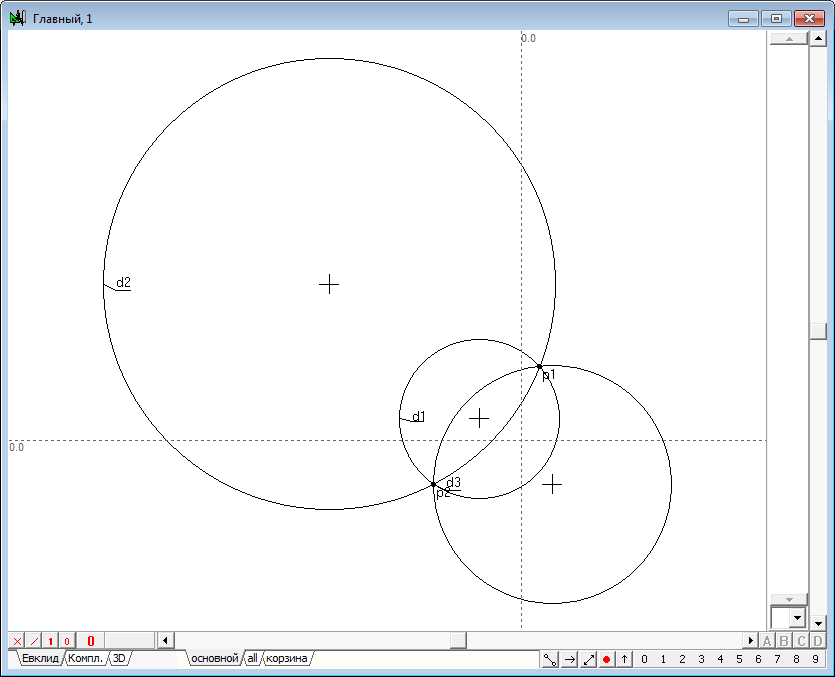
| 20 | Будем искать алгоритм решения поставленной задачи, разбив ее на несколько этапов. Прежде всего, решим задачу о построении точки в инверсии относительно окружности инверсии, используя для этой цели сопряженную окружность инверсии, причем решим эту задачу сначала для случая явного, то есть действительного результата пересечения двух окружностей инверсии. Зададим две исходные окружности d1 и d2, пересекающиеся в двух действительных точках.
Рис. 18 |
|
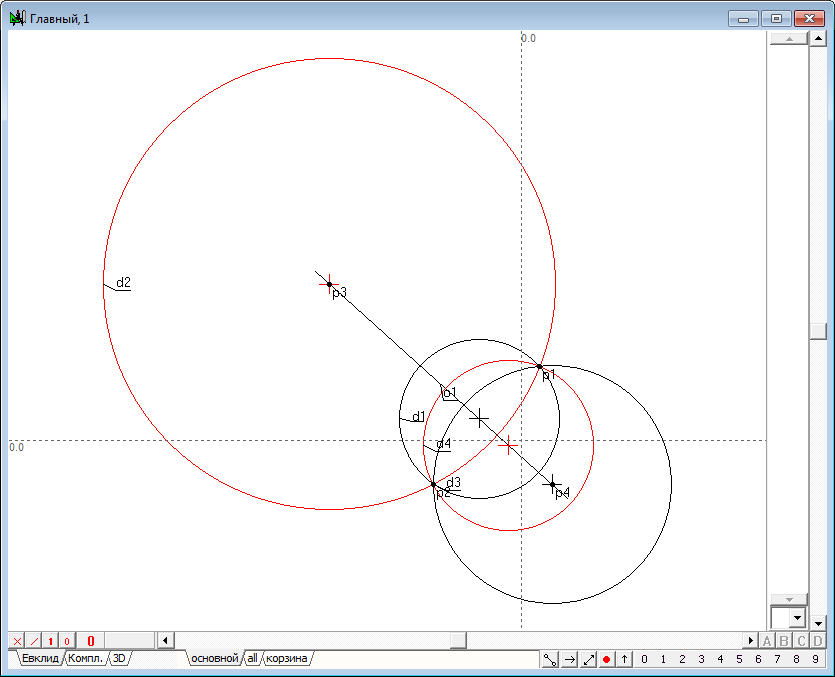
| 21 | Построим сейчас обе сопряженные окружности инверсии d3 и d4, переводящие окружности d1 и d2 друг в друга. Для этого выделим окружности d1 и d2 и нажмем на клавиатуре клавишу с латинским символом R (верхний регистр). Сейчас наличие этих окружностей нам будет необходимо для исследования их взаимосвязи при выполнении операций нахождения образа точки.
Рис. 19 |
|
| 22 | Пусть точка p1 является исходной. Преобразуем ее в операции инверсии сначала относительно окружности d3, а затем относительно окружности d4. Получим соответственно точки-образы p2 и p3. Для этого выделим точку p1, а затем, удерживая нажатой клавишу Shift, окружность d3 и нажмем на клавиатуре клавишу с латинским символом i. Аналогично поступим и с окружностью d4.
Рис. 20 |
|
| 23 | Найдем центры p4 и p5 пучка окружностей, представленного окружностями d1-d4. Для этого выделим исходные окружности d1 и d2 и нажмем на клавиатуре клавишу с латинским символом p.
Рис. 21 |
|
| 24 | Построим еще одну произвольную окружность пучка. Для этого инструментом Свободная точка разместим в произвольном месте поля чертежа точку p6, а затем, выделив вместе с ней центры пучка p4 и p5, нажмем на клавиатуре клавишу с латинским символом g.
Рис. 22 |
|
| 25 | Построим ось пучка - прямую o1. Для этого найдем центры p7 и p8 окружностей d2 и d1, выделив их и нажав на клавиатуре клавишу с латинским символом c. Затем для образования прямой o1 следует, не снимая выделения с точек p7 и p8, нажать на клавишу с латинским символом o.
Рис. 23 |
|
| 26 | Построим также радикальную ось o2 пучка окружностей, выделив точки p4 и p5 и нажав на клавиатуре клавишу с латинским символом o.
Рис. 24 |
|
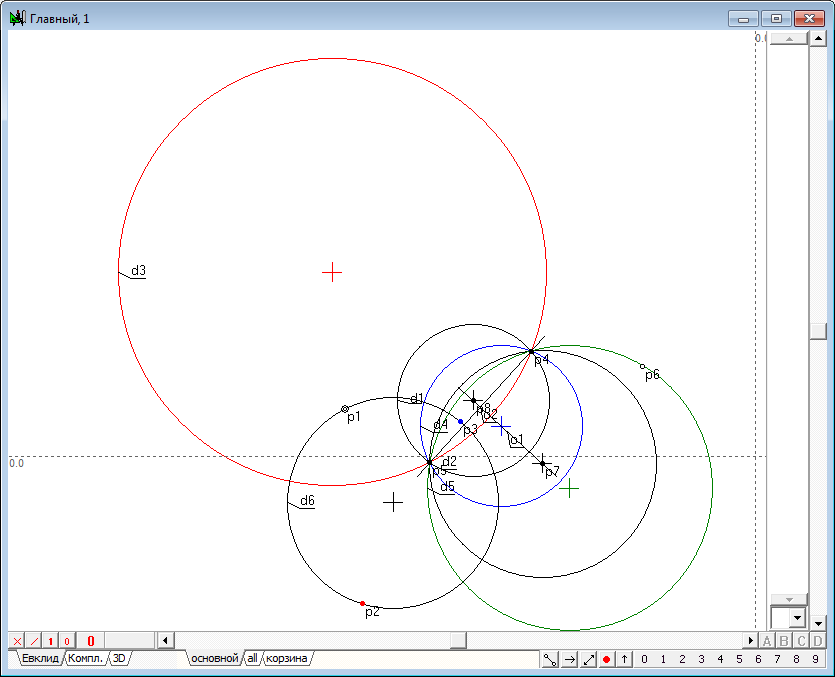
| 27 | Используя точку-прообраз p1, радикальную ось o2 и дополнительную окружность d5, построим окружность d6, проходящую ортогонально к этим объектам. Для этого выделим эти объекты и нажмем на клавиатуре клавишу с латинским символом D (верхний регистр). Обратим внимание на то, что в операции мы использовали дополнительную окружность d5, несмотря на то, что в нашем построении имеются окружности d1 и d2, с помощью которых можно было бы получить аналогичный результат. Это сделано с той целью, чтобы показать, что в будущих алгоритмах, в которых окружности d1 и d2 будут не заданы, основная задача нахождения точек инверсии все равно будет решаться и без их участия.
Рис. 25 |
|
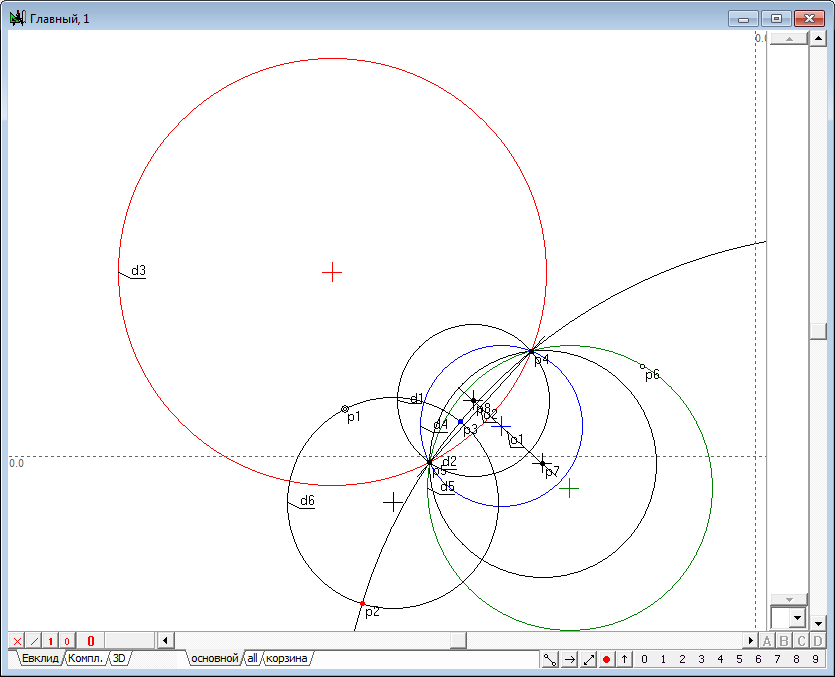
| 28 | Мы видим, что окружность d6 прошла через точки p2 и p3, которые, как мы уже отмечали, являются образами точки p1 относительно окружностей d3 и d4. Теперь поставим перед собой задачу: определить геометрическое место точки p2, зная точку p3, но, не используя при этом окружность d3. Эта задача элементарно решается, если через центры пучка p4 и p5, а также точку p3 провести окружность d7 и найти ее пересечение с окружностью d6. Для этого выделим перечисленные точки и нажмем на клавиатуре клавишу с латинским символом g. Из двух получаемых точек пересечения требуется выбрать ту, которая не совпадает с точкой p3.
Рис. 26 |
|
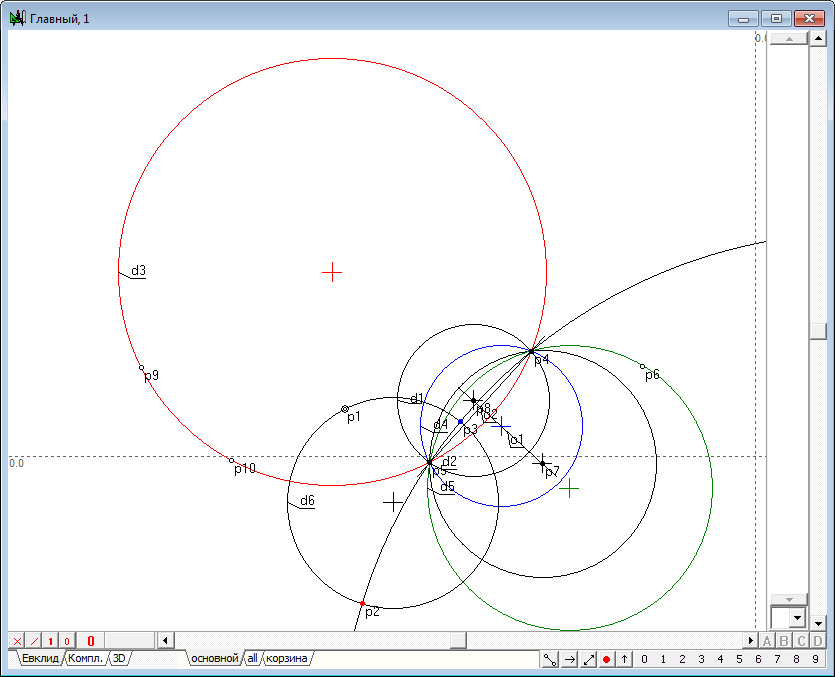
| 29 | Поставленная задача решена. Однако мы продолжим наше исследование и покажем, что тот же результат можно будет получить, не имея очерков окружностей d3 и d4, не зная точки p3 и не опираясь на окружности d1 и d2. Все что нам будет необходимо - это лишь возможность получения пары точек, инцидентных с окружностью d3, причем в общем случае, эти точки не обязательно должны быть действительными. Вообще говоря, такая пара точек может быть получена операцией пересечения произвольной прямой с окружностью. В реализуемом нами построении мы воспользуемся операцией назначения точек, инцидентных с объектом, что не повлияет на общую идею реализации алгоритма. Подведем курсор к какому-либо произвольному месту очерка окружности d3 и, удерживая нажатой клавишу Ctrl, щелкнем левой кнопкой мыши. Данная операция приведет к тому, что на окружности появится точка p9, связанная с ней. Аналогичным образом построим еще и точку p10.
Рис. 27 |
|
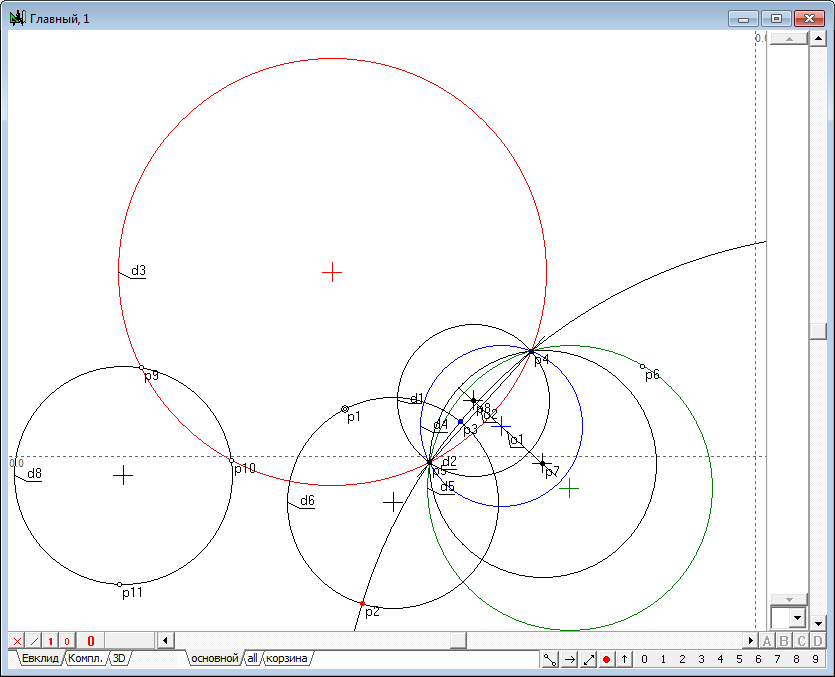
| 30 | Инструментом Свободная точка сгенерируем в каком-либо месте чертежа точку p11, а затем, выделив ее и вместе с ней точки p9 и p10, нажав на клавиатуре клавишу с латинским символом g, построим окружность d8.
Рис. 28 |
|
| 31 | Аналогично разместим на окружности еще пару точек p12 и p13, а в произвольном месте чертежа точку p14 и проведем через них окружность d9.
Рис. 29 |
|
| 32 | Проведем через точки p9 и p10 прямую o3, выделив их и нажав клавишу с латинским символом o, а затем, добавив к выделенной прямой окружности d8 и d9 и нажав клавишу с латинским символом D (верхний регистр), построим окружность d10, ортогональную к выделенным объектам. Обратим внимание на то, что эта окружность ортогональна также и окружности d3, а значит, она может быть использована как сопряженная окружность инверсии при нахождении образа точки p1 по отношению к "отсутствующей" окружности d3.
Рис. 30 |
|
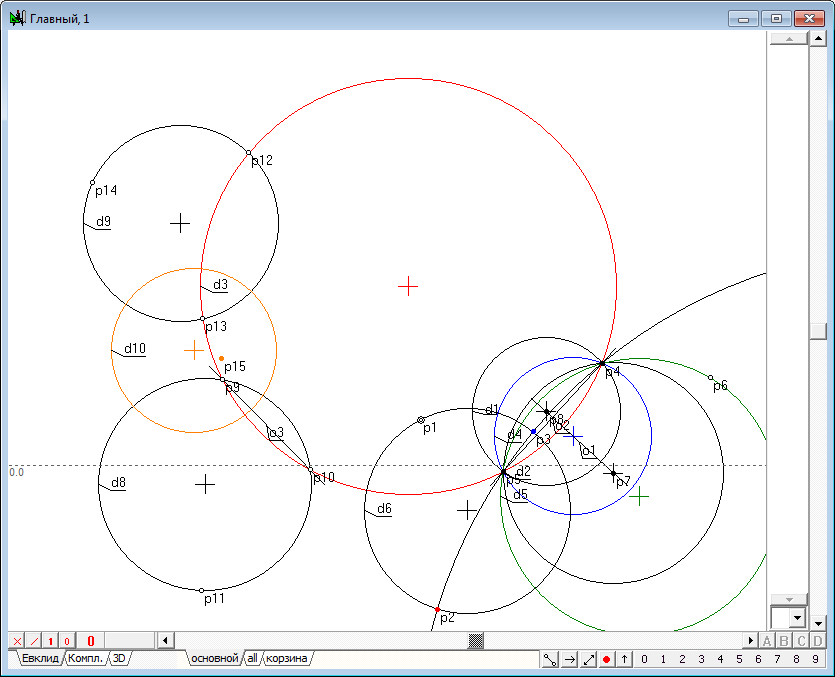
| 33 | Построим теперь образ p15 точки p1 в инверсии относительно окружности d10.
Рис. 31 |
|
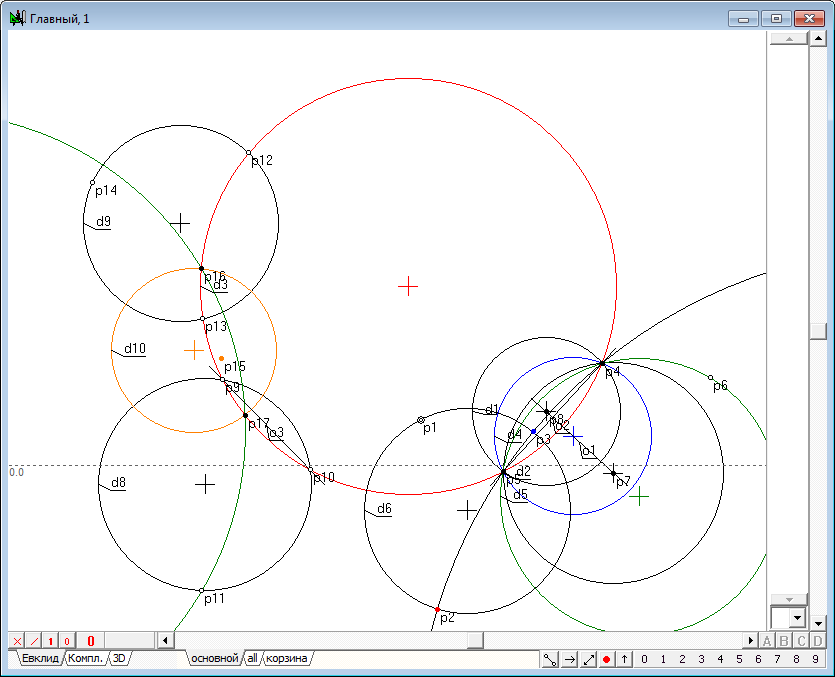
| 34 | Найдя точки пересечения p16 и p17 окружности d10 с окружностью d3 (выделив d10 и d3 и нажав на клавишу с латинским символом p), добавим к полученному выделению произвольную точку, например, p11, проведем через них окружность, нажав клавишу с латинским символом g.
Рис. 32 |
|
| 35 | Проведем через p1 и p15 окружность d12, ортогональную к окружности d10, выделив эти объекты и нажав на клавишу с латинским символом D (верхний регистр). Из чертежа видно, что окружность d12 прошла через искомую нами точку p2. Однако само ее геометрическое место нами пока не определено.
Рис. 33 |
|
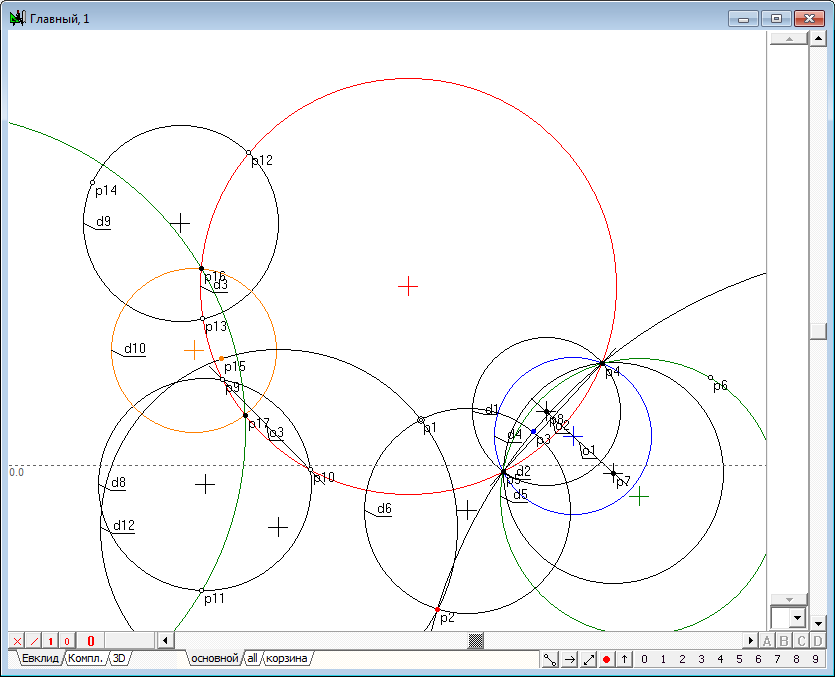
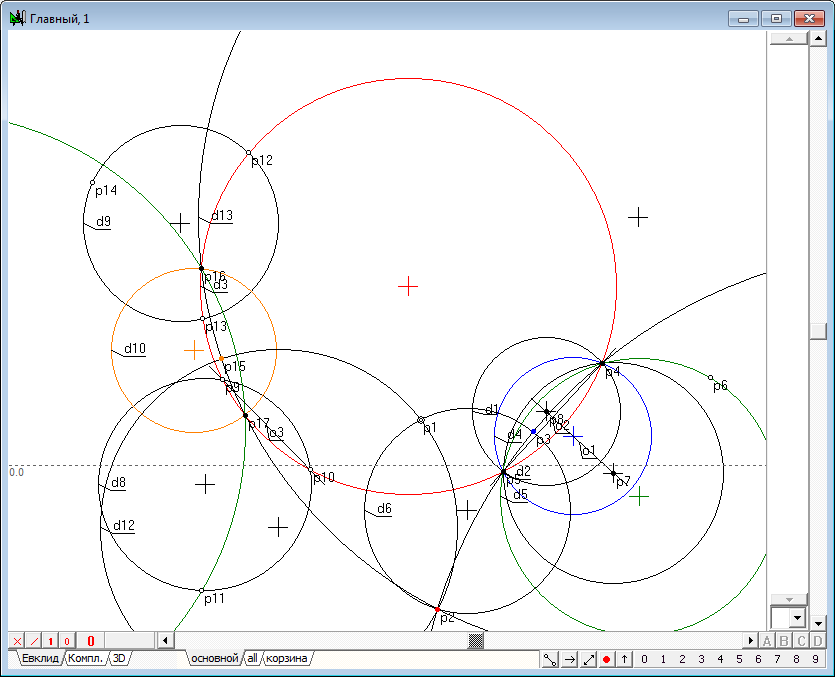
| 36 | Для завершения решения задачи проведем через p15, p16 и p17 окружность d13, выделив их и нажав клавишу с латинским символом g.
Рис. 34 |
|
| 37 | Таким образом, геометрическое место образа точки p1 в инверсии относительно окружности d3 найдено путем построения произвольной сопряженной к ней окружности инверсии опосредовано. Полученный алгоритм позволяет сформулировать и решить задачу о построении образа точки в инверсии, учитывая тот случай, когда окружность инверсии не имеет явного очерка, в частности, если центр этой окружности является вещественным, а радиус - мнимым. Создадим такой алгоритм, оформим его в качестве самостоятельной процедуры и выполним его тестирование. | |
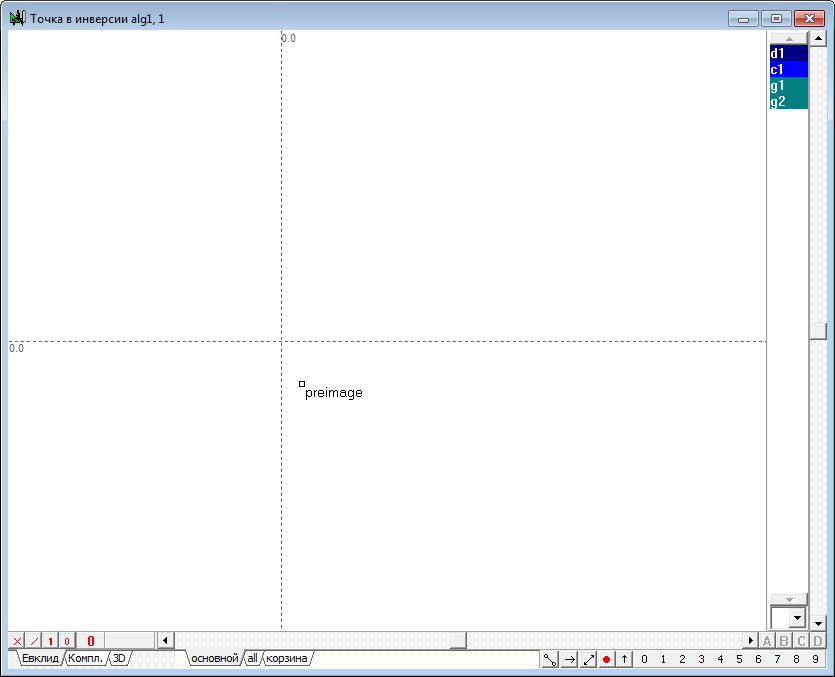
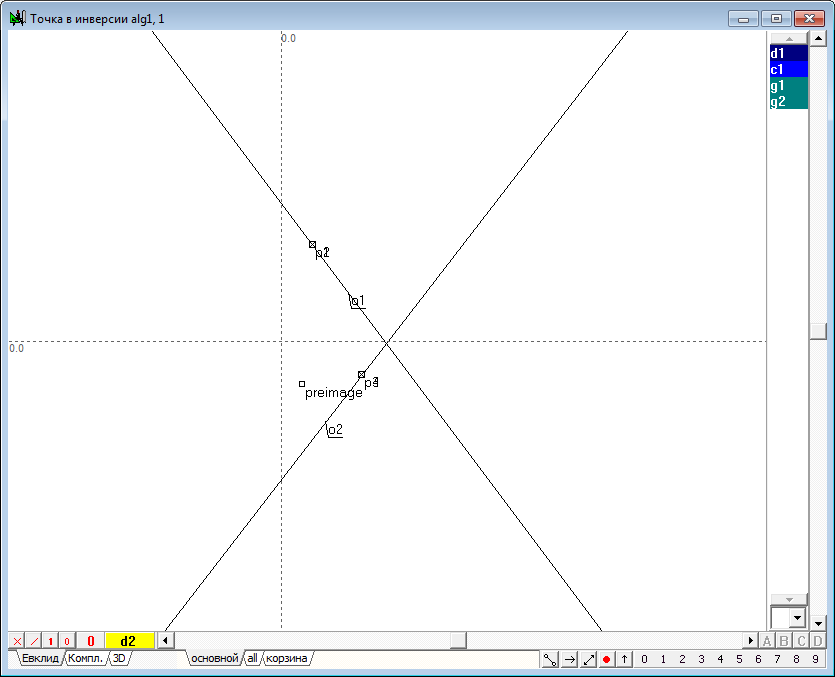
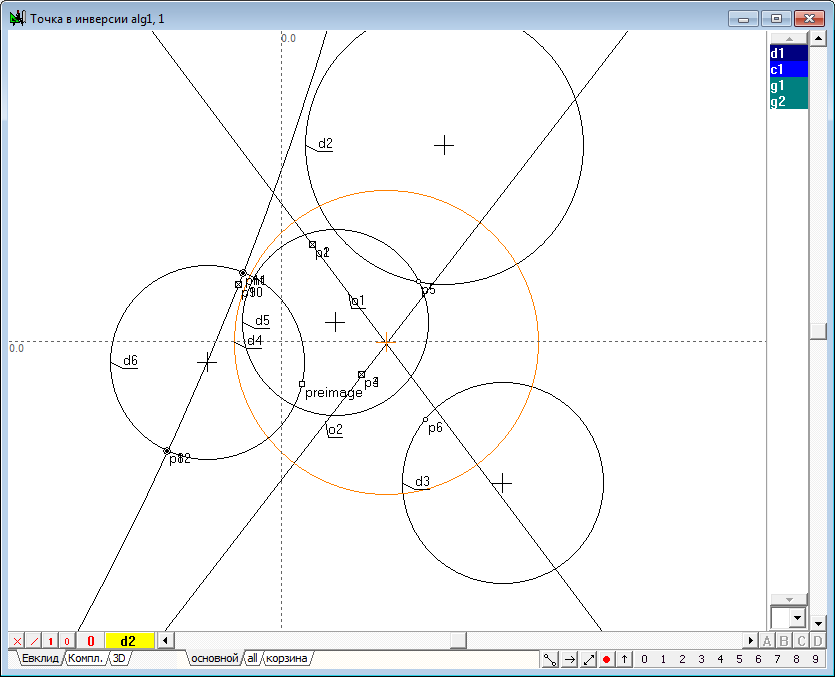
| 38 | Пусть задана окружность d1 с вещественным центром и мнимым радиусом. Инструментом Свободная точка разместим точку preimage, которую будем переводить в инверсии относительно окружности d1.
Рис. 35 |
|
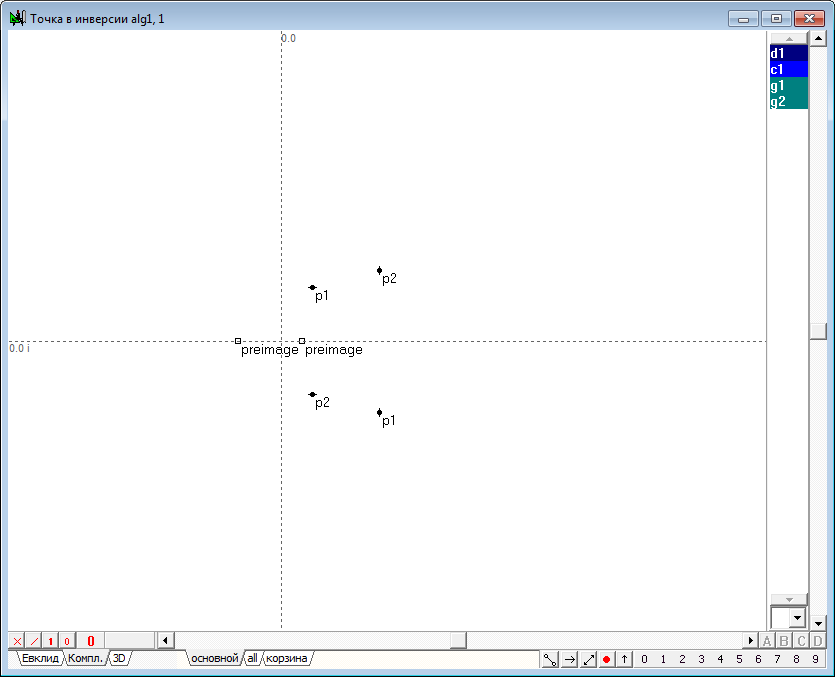
| 39 | Инструментом Свободная прямая проведем две произвольные прямые o1 и o2 и найдем точки p1, p2, p3, p4 их пересечения с окружностью d1. Для этого, удерживая нажатой клавишу Shift, выделим прямую o1 и метку с именем мнимой окружности d1, после чего нажмем клавишу с латинским символом p. В окне алгоритма отобразятся маркеры мнимых точек в виде двух совпадающих перечеркнутых квадратиков, которым соответствуют вещественные компоненты координат этих точек. Такие маркеры можно использовать для выделения мнимых точек аналогично тому, как осуществляется выделение указанием курсора мыши на очерки и изображения других геометрических объектов. В данном случае два маркера визуально совпадают, потому что обе точки имеют одинаковые вещественные компоненты координат, однако мнимые компоненты координат этих точек различны, в чем можно убедиться, обратившись к протоколу значений объектов (вызывается комбинацией клавиш Ctrl+O), либо, переключившись на закладку Компл., включающую режим отображения объектов комплексной плоскости и находящуюся в левой нижней части окна реализации алгоритма.
Рис. 36 |
|
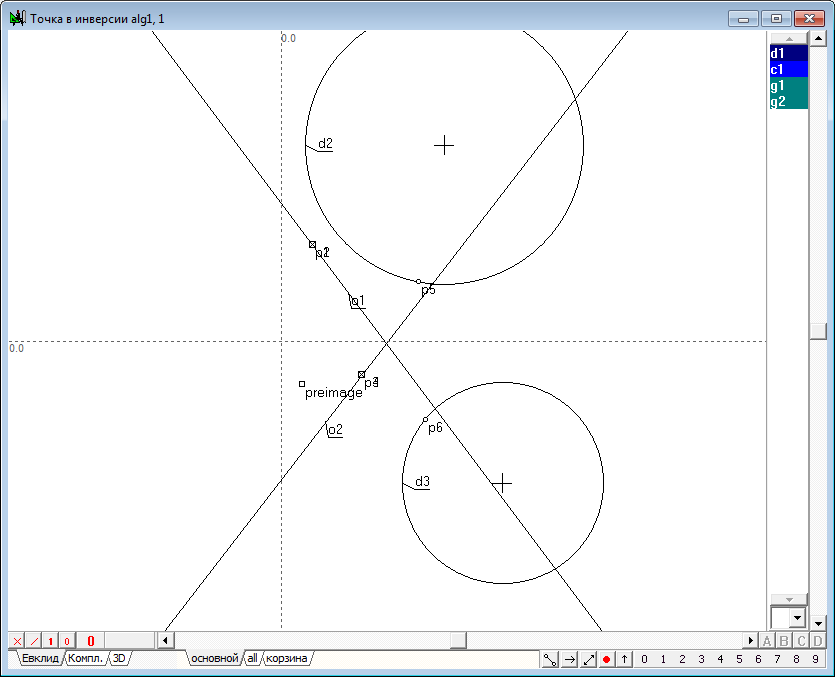
| 40 | Аналогичными действиями построим точки p3 и p4 пересечения прямой линии o2 с мнимой окружностью d1.
Рис. 37 |
|
| 41 | Построим теперь две произвольные точки p5 и p6 и проведем через p5, p1 и p2 окружность d2, а через точки p6, p3 и p4 - окружность d3. Для построения окружностей следует выделить соответственные точки и нажать клавишу с латинским символом g.
Рис. 38 |
|
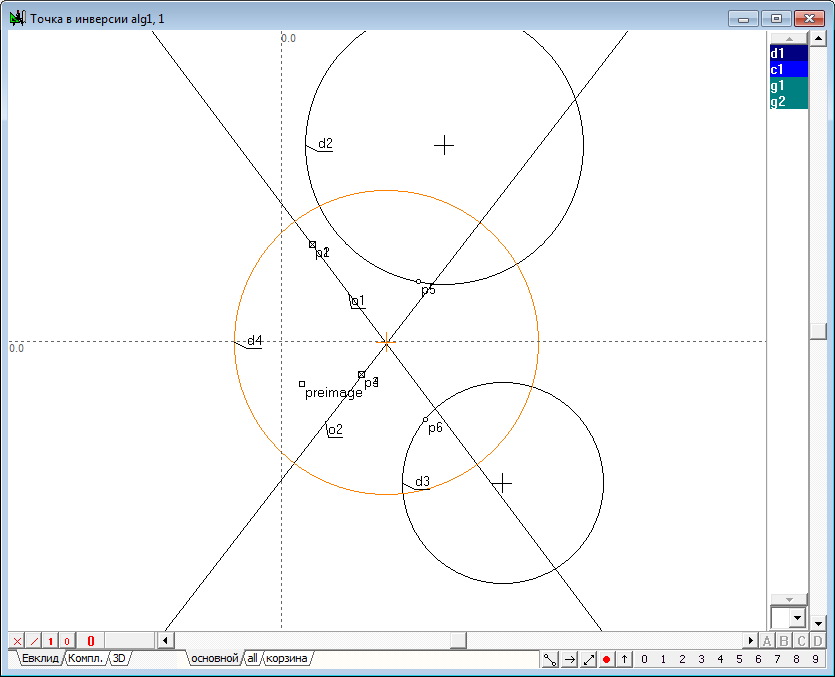
| 42 | Поскольку прямая линия o1 является радикальной осью пары окружностей d1-d2, то для построения окружности d4, ортогональной к d1, выделим прямую o1, окружности d2 и d3 и нажмем на клавишу с латинским символом D (верхний регистр). Окружность d4 является сопряженной окружностью инверсии к окружности d1.
Рис. 39 |
|
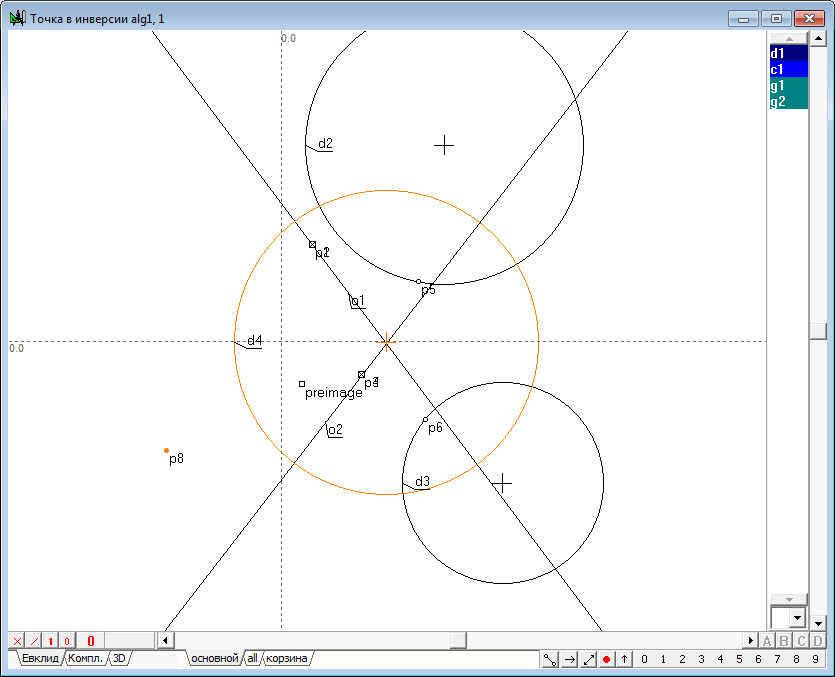
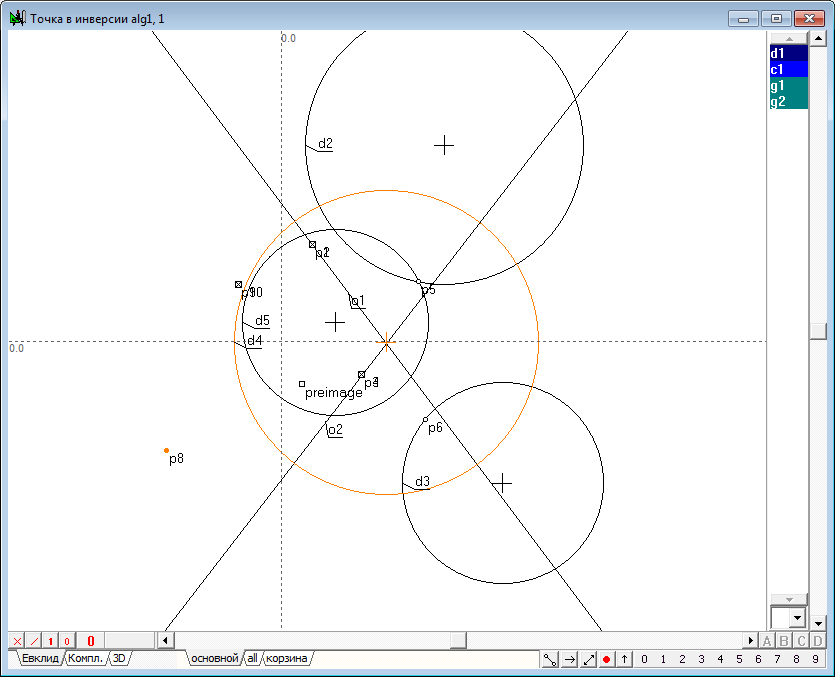
| 43 | Построим точку p8 - образ точки preimage в инверсии относительно окружности d4.
Рис. 40 |
|
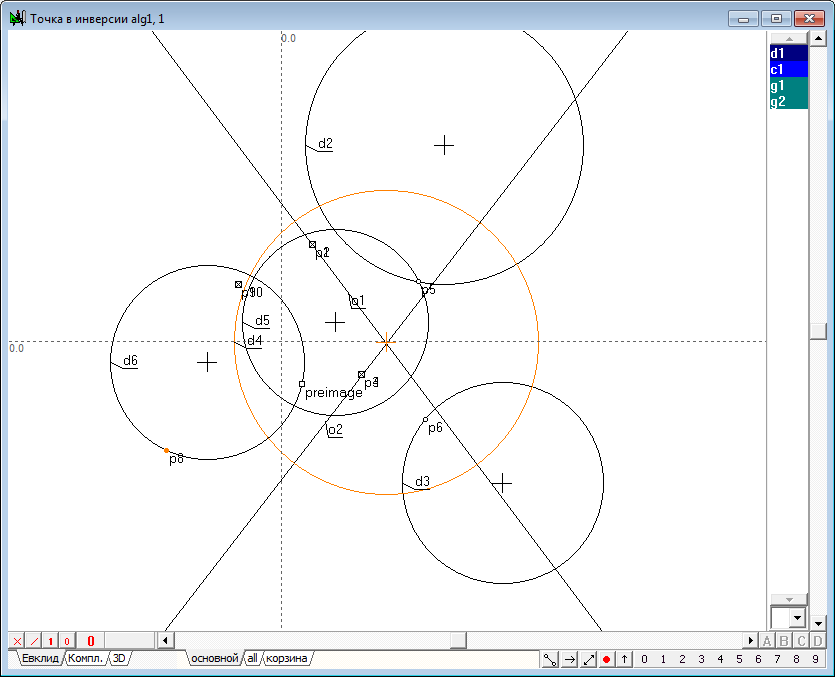
| 44 | Построим дополнительную окружность d5 пучка окружностей, задаваемого сопряженными окружностями инверсии d1 и d4. Для этого найдем точки p9 и p10 их пересечения, выделив окружность d4 и метку мнимой окружности d1 и нажав после этого на клавишу с латинским символом p, затем, добавив к выделению точку p5 (которая, вообще говоря, может быть произвольной), нажмем на клавишу с латинским символом g.
Рис. 41 |
|
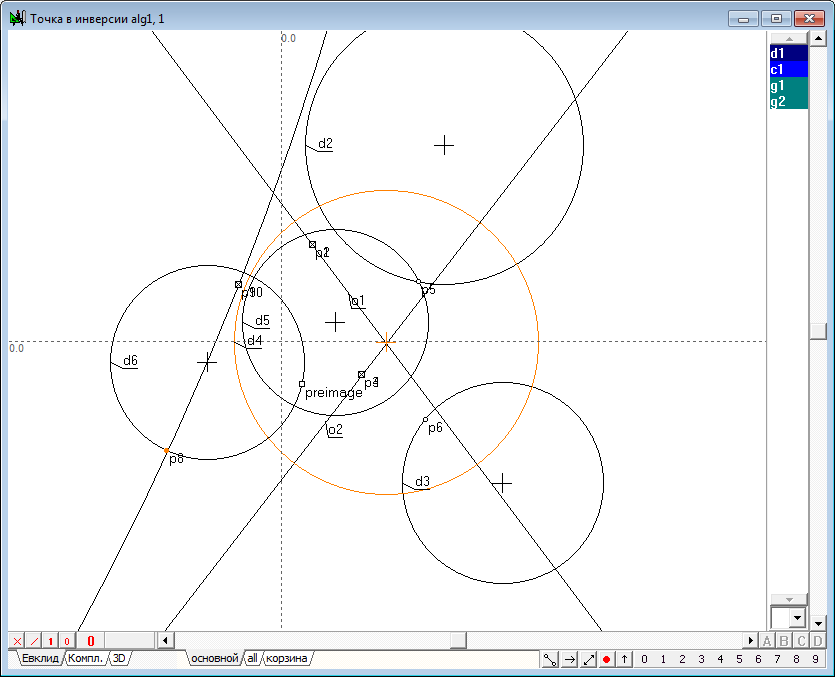
| 45 | В предыдущем примере было показано, что искомая точка - образ точки preimage в инверсии относительно окружности d1 должна находиться на окружности d6, проходящей через точки пересечения ортогональной окружности d4 с исходной окружностью - центры пучка - перпендикулярно к окружностям этого пучка, в частности, к построенной дополнительной окружности d5. Для этого выделим точки preimage, p5 и окружность d5 и нажмем на клавишу с латинским символом D (верхний регистр). Заметим, что использовать окружность d4 вместо окружности d5 нельзя, поскольку в этом случае было бы невозможно провести ортогональную окружность, наподобие d6, однозначно.
Рис. 42 |
|
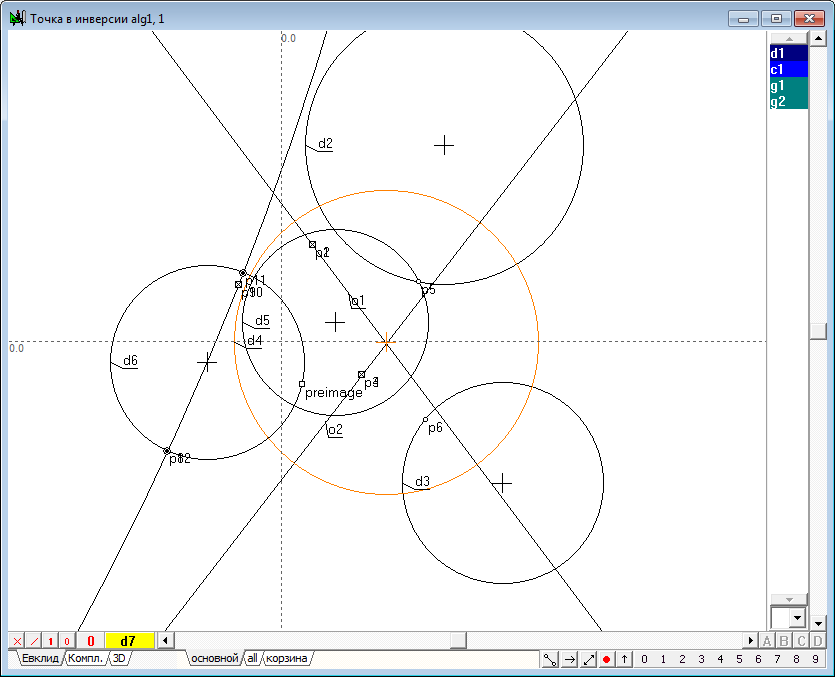
| 46 | Определение конкретного положения искомой точки выполним, проведя окружность d7 через точку p8 и центры пучка - точки p9 и p10, для чего выделим все эти точки и нажмем на клавишу с латинским символом g.
Рис. 43 |
|
| 47 | Нам остается найти точки p11 и p12 пересечения окружностей d6 и d7, после чего выбрать в качестве ответа точку, не совпадающую с точкой p8. Для того чтобы сделать такой выбор, определим расстояние с1 между точками p8 и p11, выделив точки и нажав на клавишу с латинским символом l. В результате будет определено расстояние между точками p8 и p11, а метка, обозначающая величину c1, появится в списке невизуальных объектов.
Рис. 44 |
|
| 48 | Воспользовавшись функцией Неравенство X< Y определим условие g1 с аргументами X: 0.001 (используемая для задания малой величины) и Y: расстояние c1. Если расстояние между точками p8 и p11 будет превышать значение 0.001, то условие g1 будет истинным, если же точки p8 и p11 практически совпадут, то условие будет ложным. Второе условие g2 зададим функцией Логическое отрицание not с аргументом g1. Значение g2 будет противоположным (инверсным) по отношению к значению g1. Окончательный выбор необходимой точки осуществим с помощью функции Селектор. Эта функция будет передавать в выходной параметр pnt значение точки p11 при условии истинности g1 или p12 при условии истинности g2.
Рис. 45 |
|
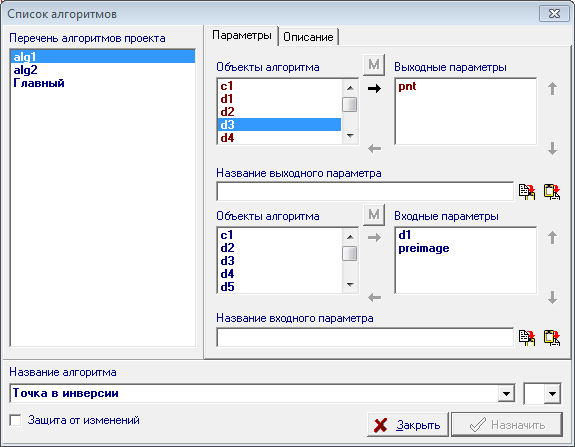
| 49 | В качестве входных параметров алгоритма укажем окружность d1 и точку preimage. Для этого выделим их и во всплывающем контекстном меню окна реализации алгоритма выберем пункт: Назначить d1, preimage входом алгоритма. Параметру d1 дадим название Окружность инверсии, а параметру preimаge название Точка. Затем откроем окно настройки параметров алгоритма комбинацией клавиш Alt+A и, выделив в списке объектов алгоритма, отвечающем за назначение выходных параметров, объект pnt перенесем его при помощи кнопки Стрелка вправо в список Выходных параметров. Назначим этому параметру название Образ. Дадим алгоритму название Точка в инверсии. С этого момента алгоритм можно использовать, как процедуру, в других алгоритмах проекта. Рис. 46 |
|
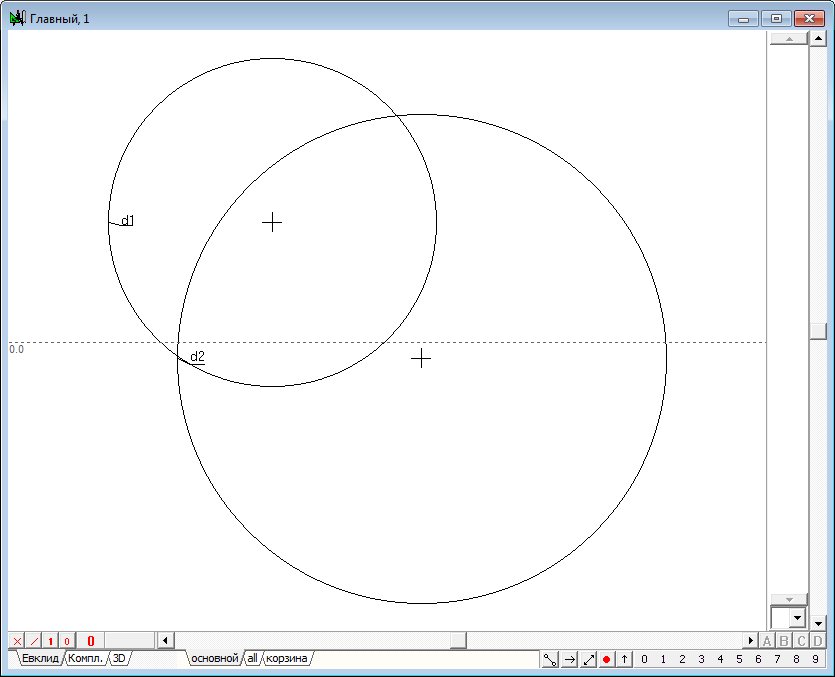
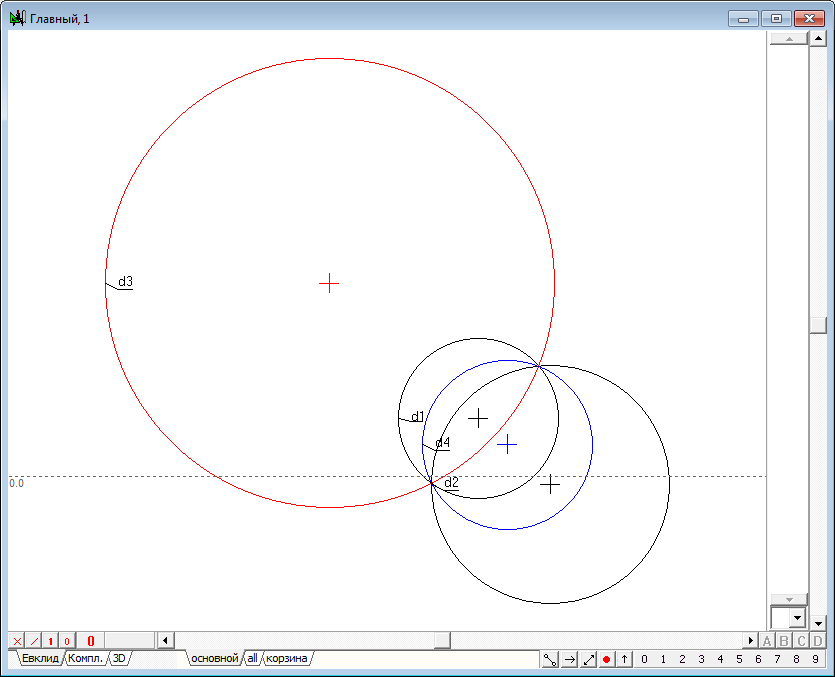
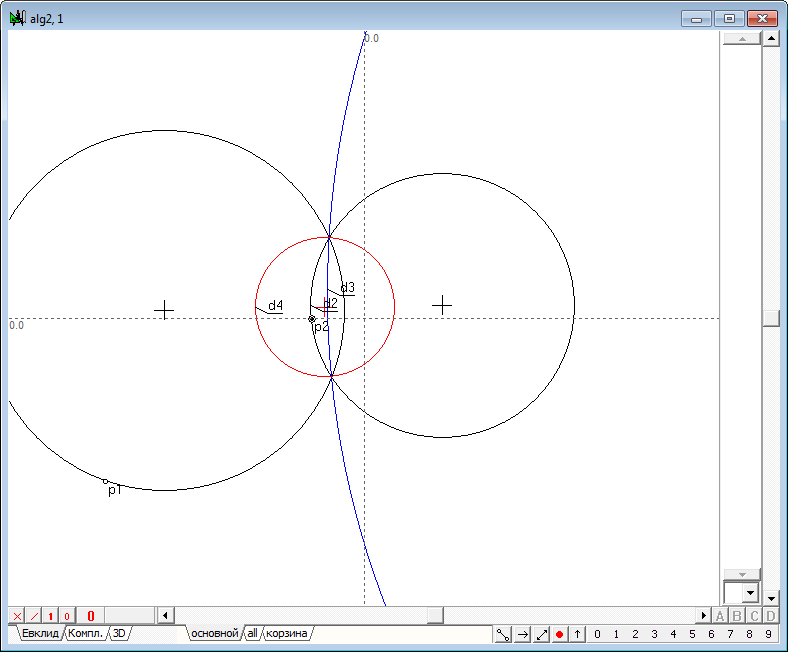
| 50 | Для проверки корректности и работоспособности разработанной процедуры сгенерируем тестовый алгоритм. Создадим его с помощью комбинации клавиш Ctrl+Alt+N. Выполним следующее построение: 1. Построим явно пересекающиеся окружности d1 и d2, а затем, выделив их и нажав на клавишу с латинским символом R (верхний регистр), построим две окружности инверсии d3 и d4. Для того чтобы легче различать их, изменим их цвета с черного, например, на красный и синий. Затем, разместив где-либо на поле чертежа свободную точку p1, преобразуем ее с помощью только что разработанной функции, вызвав ее из пункта меню Отношения/Процедуры/Точка в инверсии... В качестве Окружности инверсии укажем окружность d4, а в качестве Точки - точку p1, после чего нажмем на кнопку Ввод и получим искомый образ - точку p2. Теперь можно убедиться в том, что, перемещая шейпером точку p1 по окружности d1 мы будем получать точку p2, перемещающуюся по окружности d2, что подтверждает работоспособность нашей функции. Если же перемещать точку p1 вдоль окружности d2, то ее образ в инверсии относительно окружности d4 будет перемещаться вдоль окружности d1.
Рис. 47 |
|
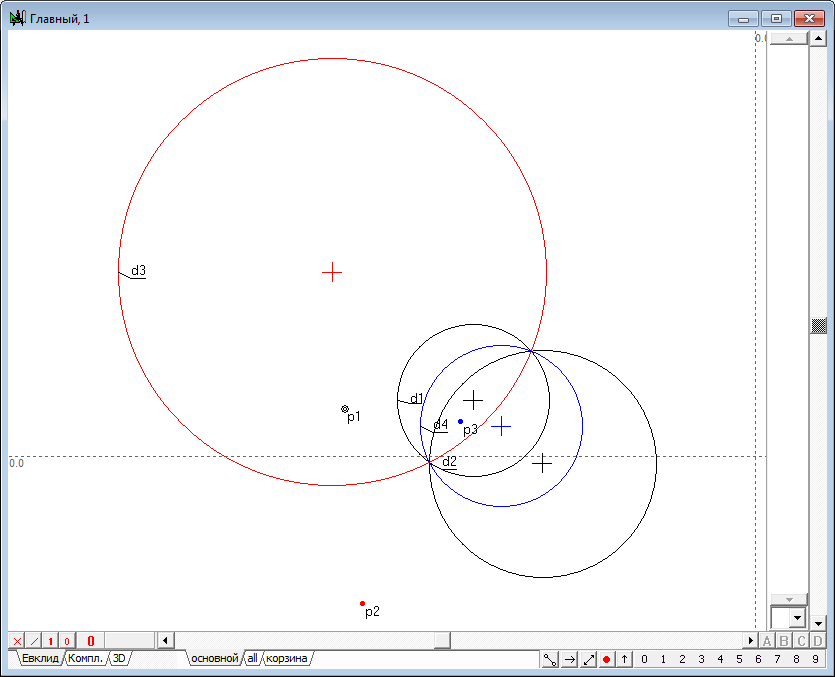
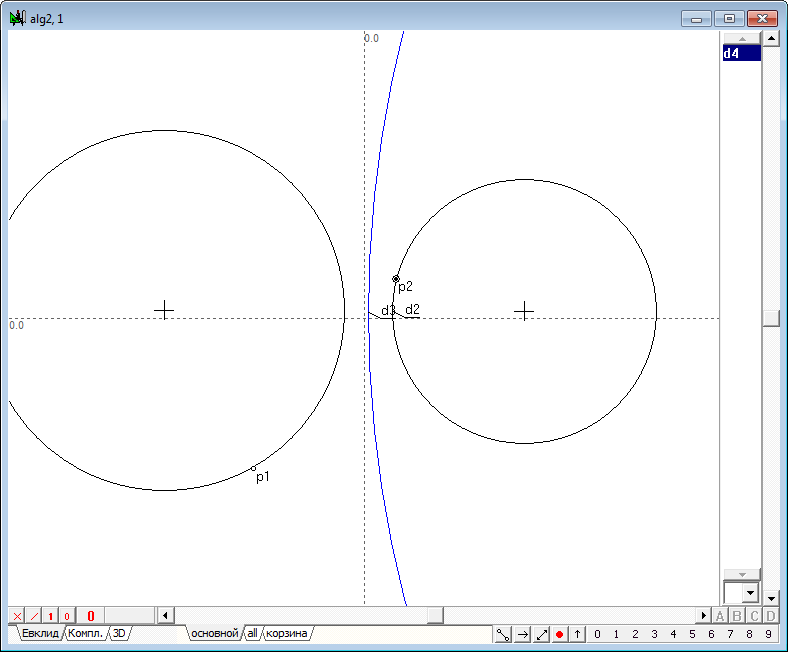
| 51 | Если же теперь сместить центр окружности d2 вправо так, что окружность d4 исчезнет, то есть перейдет в мнимую окружность, то, несмотря на это операция инверсии будет все равно выполняться и перемещение точки p1 вдоль одной исходной окружности будет вызывать соответственное перемещение точки p2 вдоль другой исходной окружности. При движении же точки p1 вдоль второй исходной окружности точка-образ p2 будет перемещаться вдоль первой исходной окружности, что подтверждает корректность и работоспособность синтезированного алгоритма в случае определения операции инверсии на мнимой окружности.
Рис. 48
Рис. 49 |
|
| Пример |