|
|||
Зададимся целью построить сферы, касательные к четырем сферам, заданным в трехмерном пространстве. Решение этой задачи будет опираться на решения нескольких предыдущих задач, рассмотренных в следующих уроке Сфера, ортогональная к четырем заданным сферам. |
|||
| 1 | Наметим план решения задачи: 1. Построим плоскость подобия четырех сфер; Приступим к ее реализации |
||
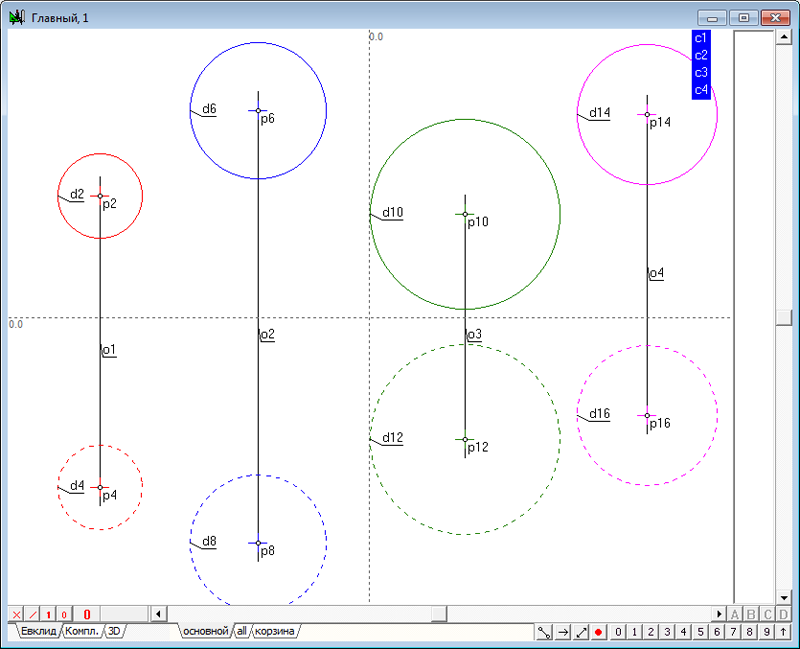
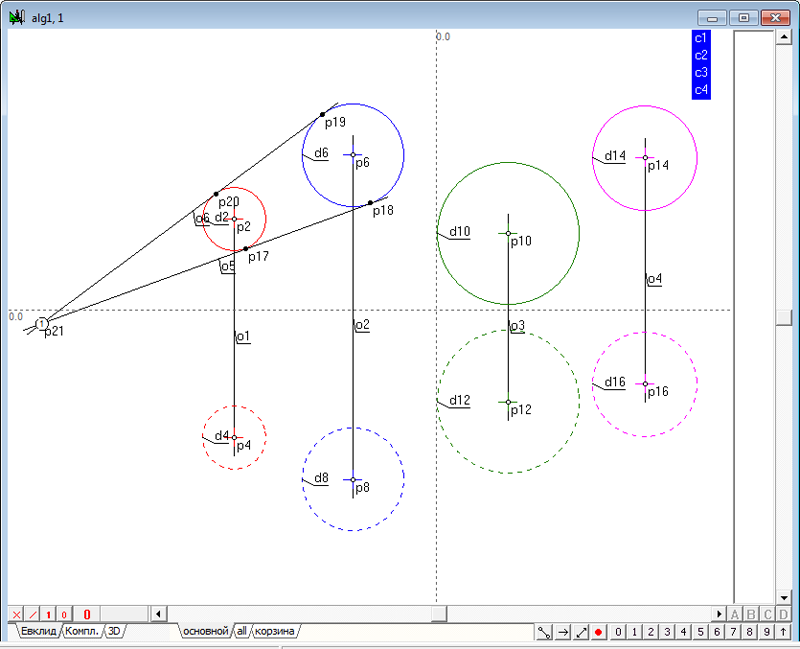
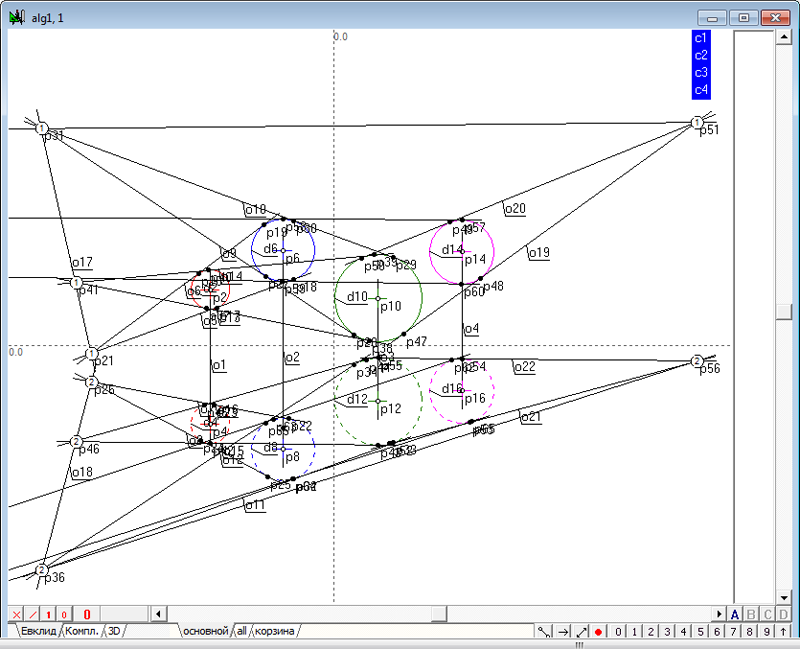
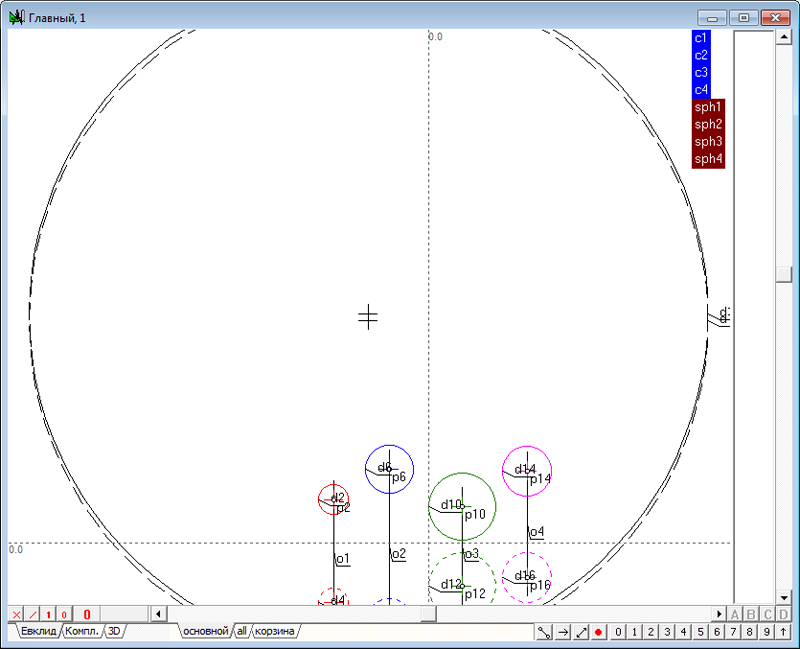
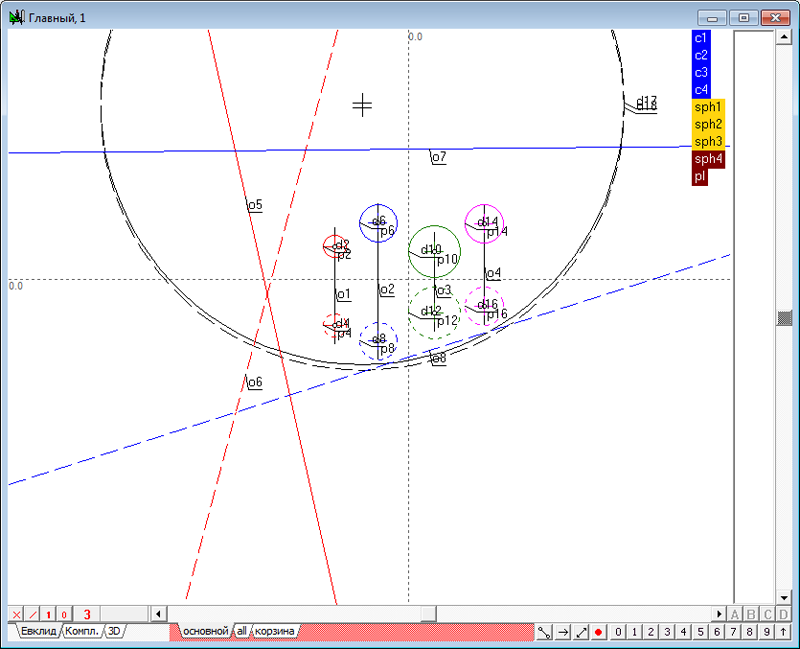
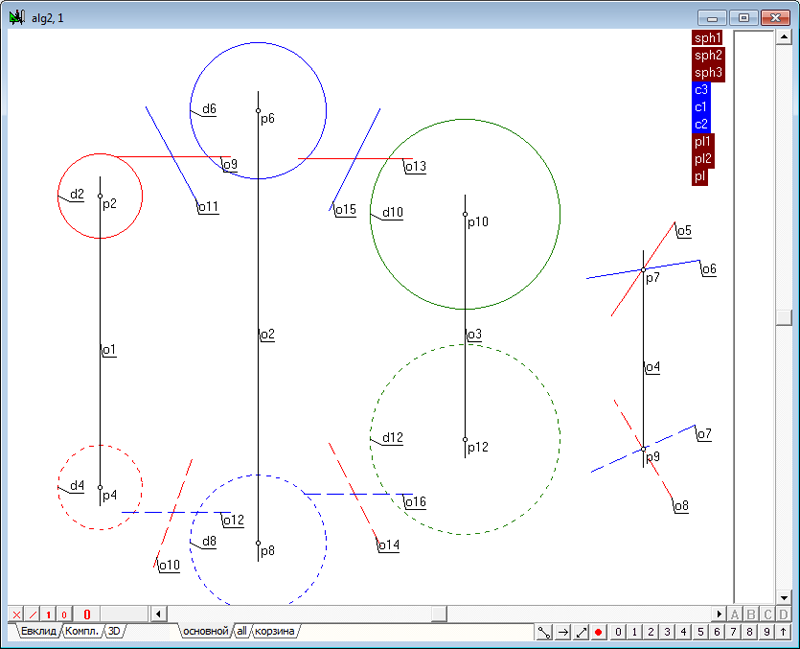
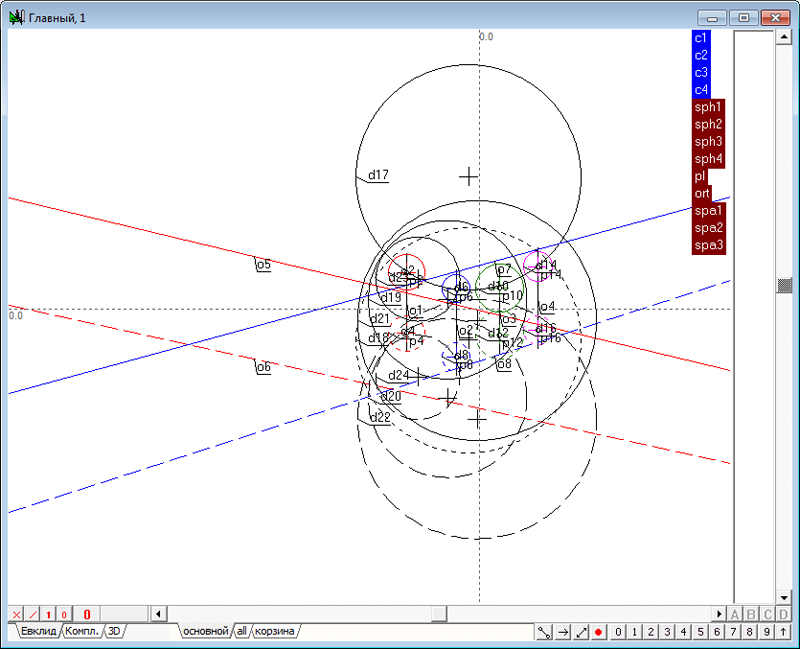
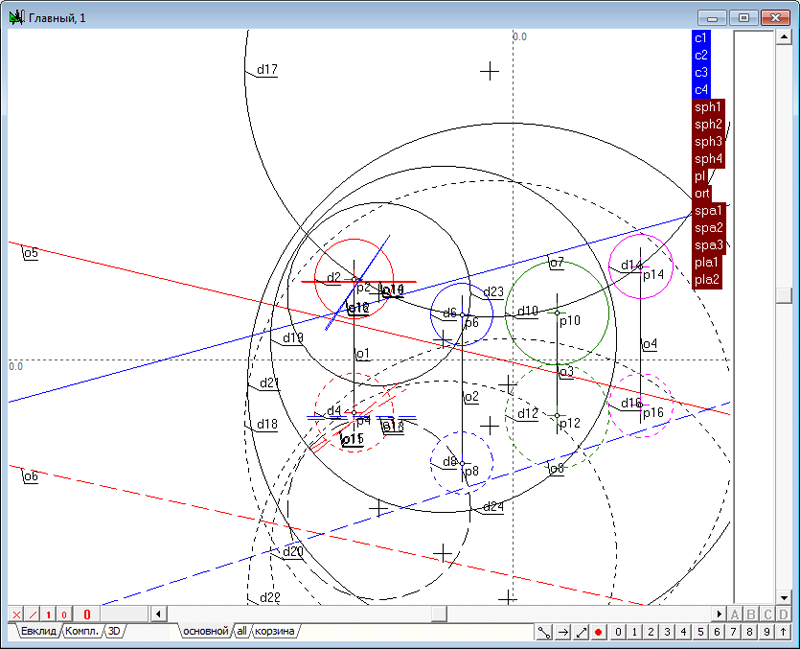
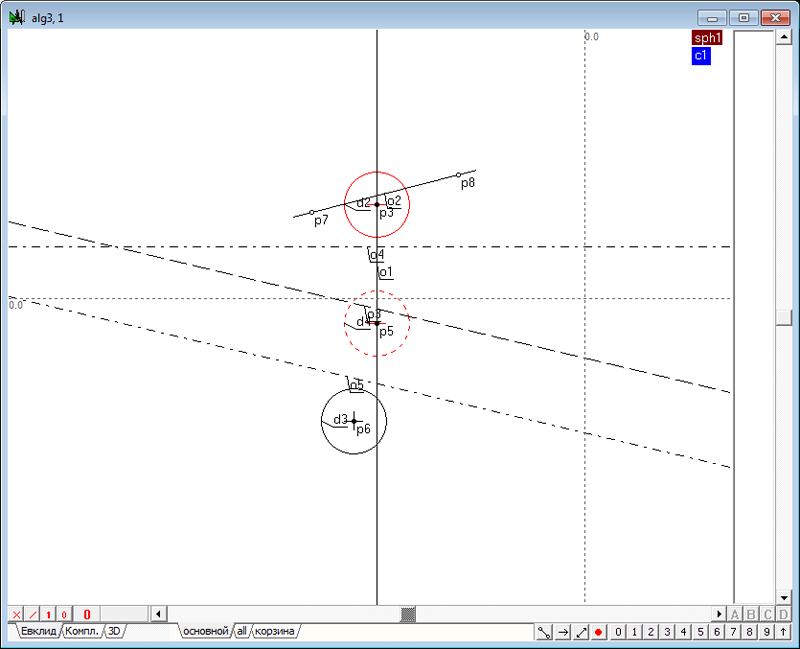
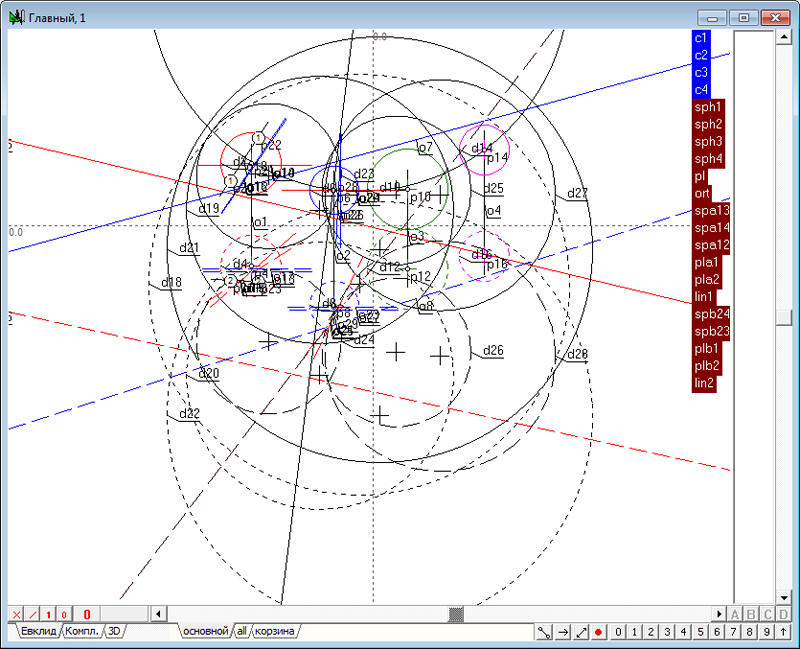
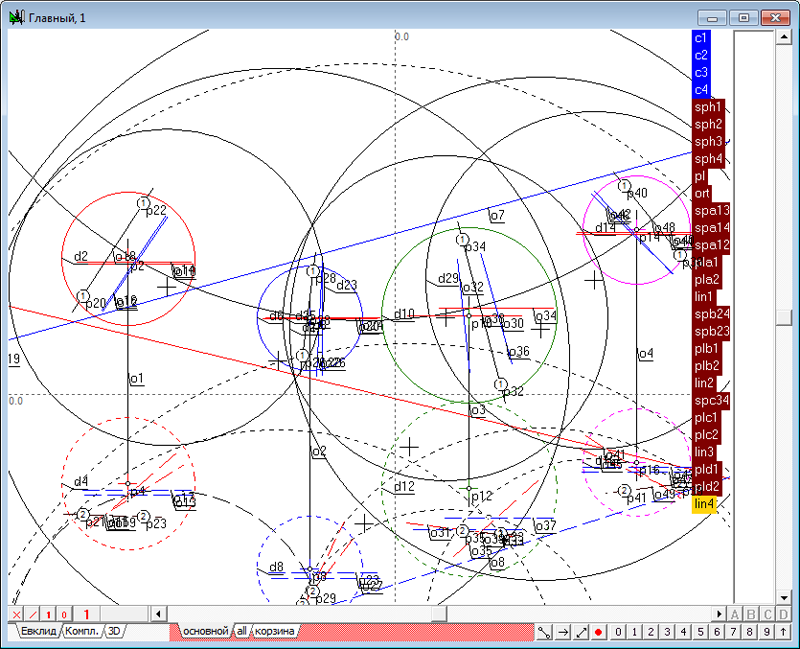
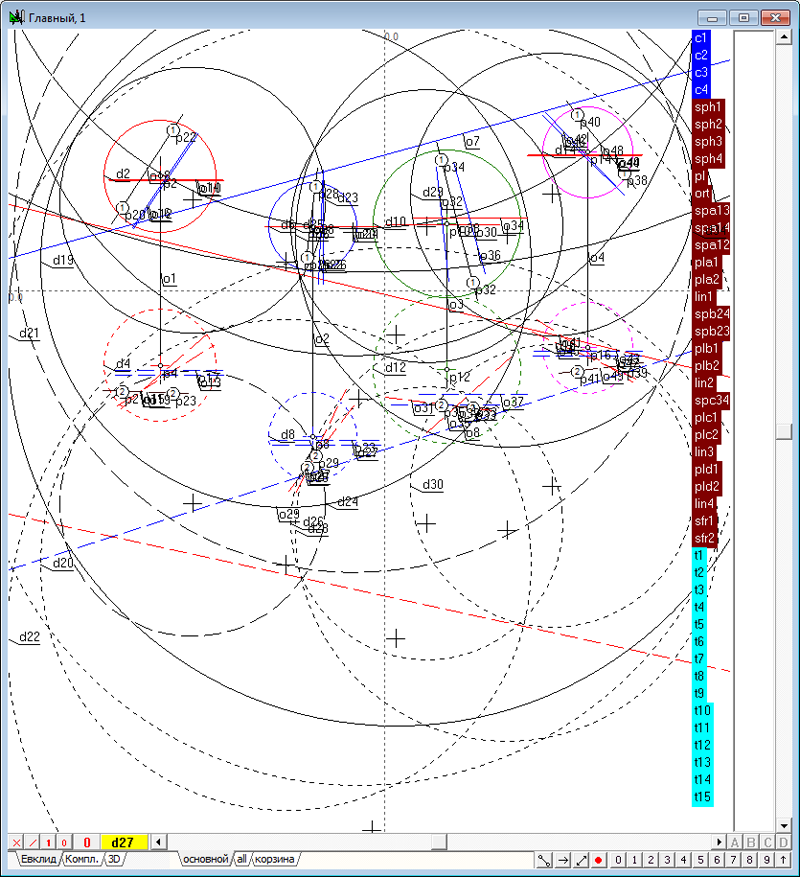
| 2 | Зададим в пространстве четыре сферы. Для этого необходимо выполнить действия, аналогичные пунктам 2 - 5 в задаче Сфера, ортогональная к четырем заданным сферам. Создадим новый проект и в окне алгоритма Главный, в котором поместим модели четырех исходных сфер.
Рис. 1 |
||
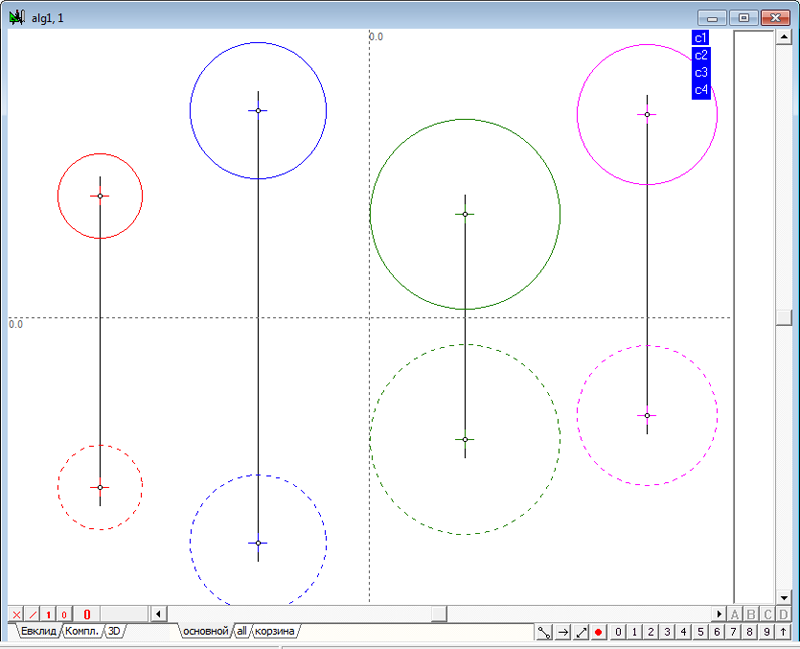
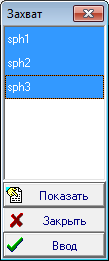
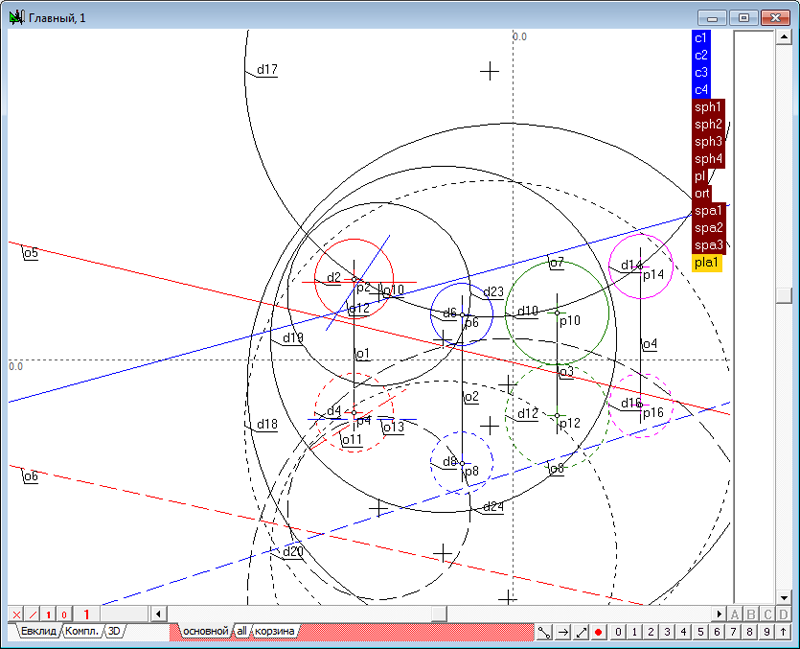
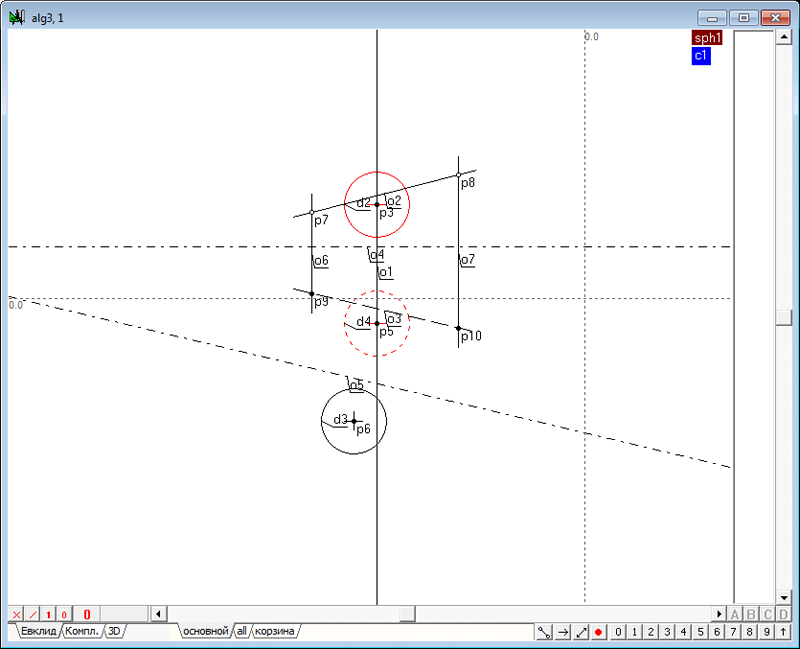
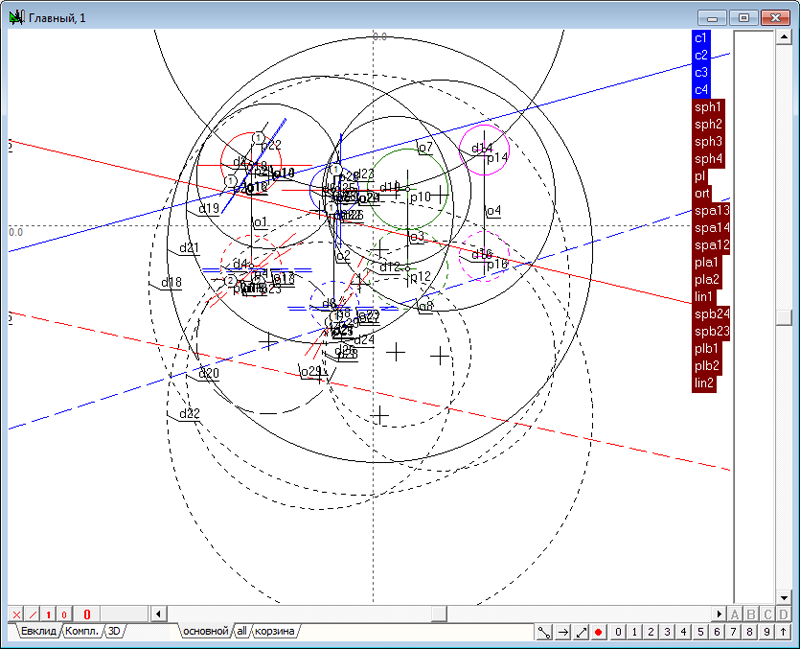
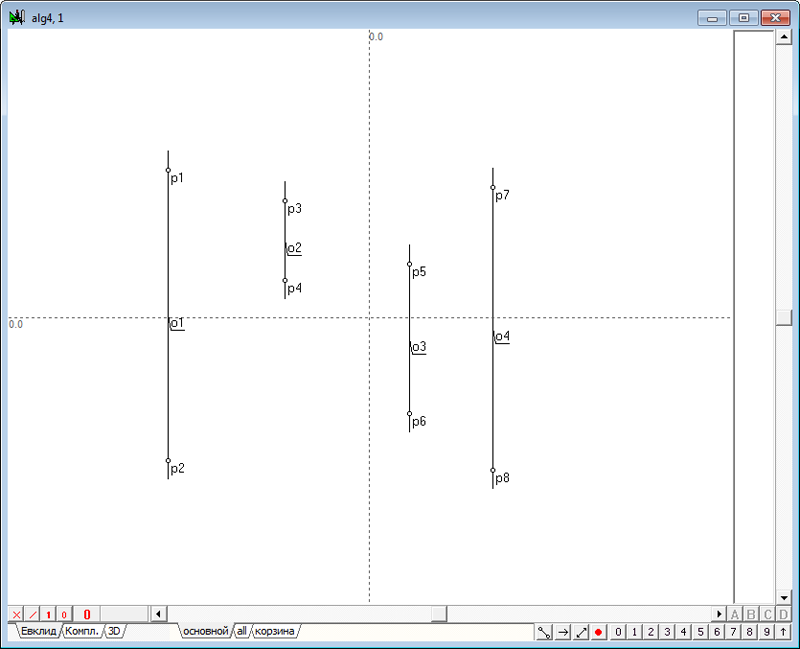
| 3 | Найдем плоскость подобия этих сфер. Оформим эту задачу в виде отдельного алгоритма, которым при необходимости можно будет воспользоваться в других задачах. Введем команду создания нового алгоритма нажатием комбинации клавиш Ctrl+Alt+N. Для формирования исходных данных нового алгоритма - четырех произвольных сфер, воспользуемся уже имеющимся построением. Скопируем исходные сферы главного алгоритма в алгоритм alg1. Для этого перейдем в главный алгоритм, выберем все имеющиеся объекты при помощи комбинации клавиш Ctrl+A и скопируем выделенное построение в буфер Clipboard, например с помощью команды Ctrl+C. В появившемся диалоговом окне выбора варианта копирования укажем опцию Отношение, а затем, подтвердив намерение выделить все объекты, нажмем на кнопку ввод. Перейдем в окно алгоритма alg1 и исполним с помощью комбинации клавиш Ctrl+V команду вставки построения из буфера Clipboard в алгоритм, при этом выберем вариант вставки построения, обозначенный опцией "Обыкновенная вставка". Результатом выполненных действий станет построение моделей четырех сфер в окне алгоритма alg1.
Рис. 2 |
||
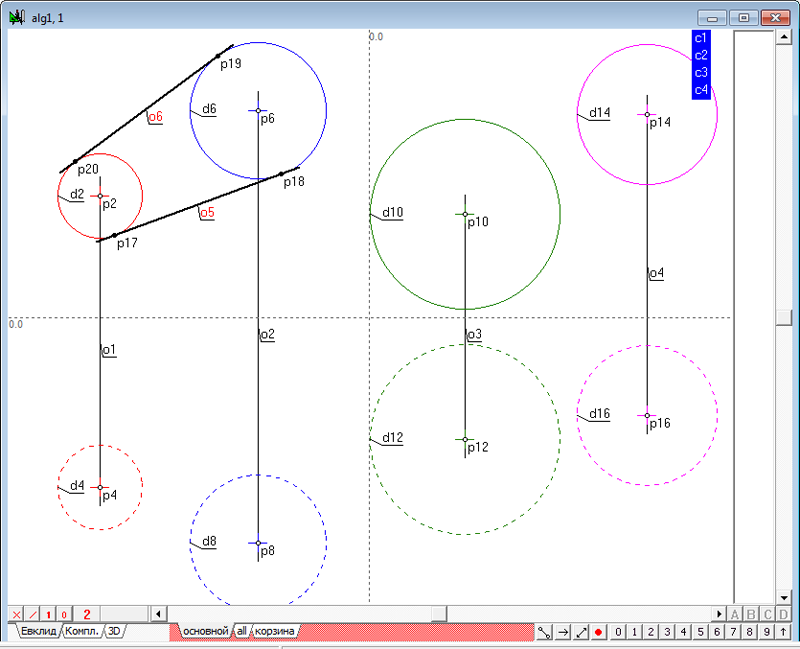
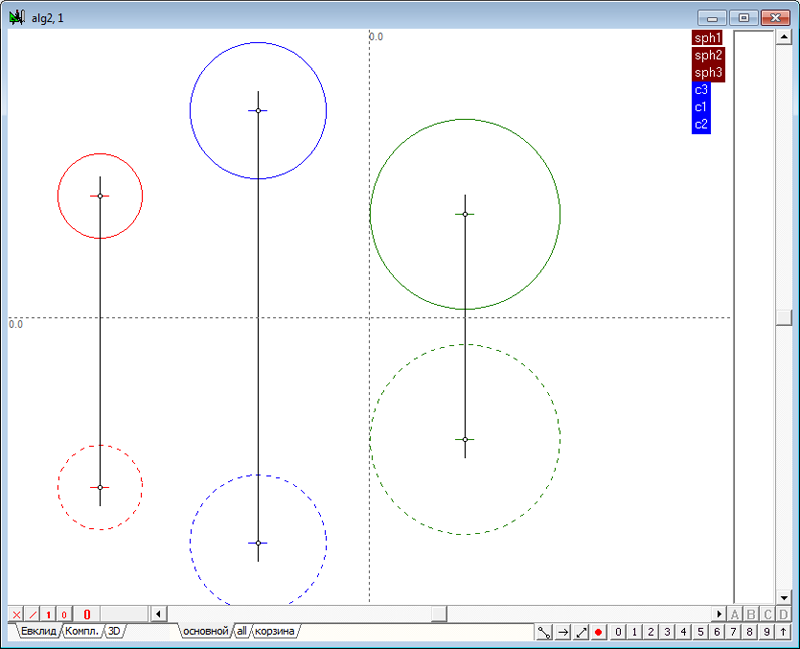
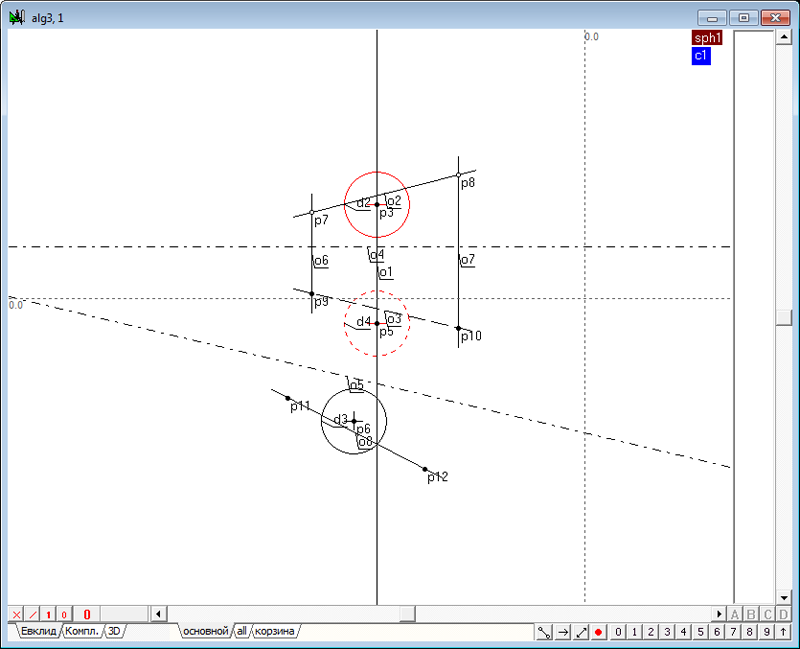
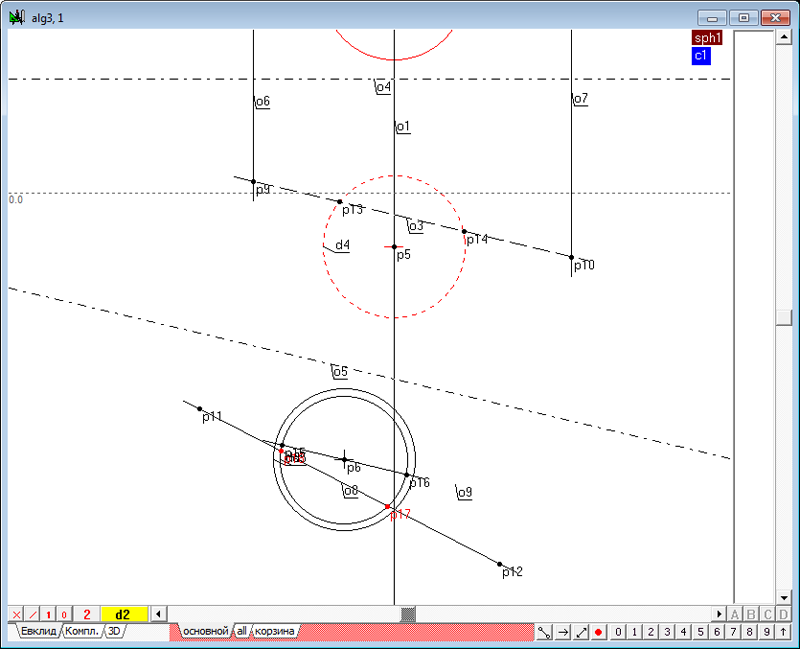
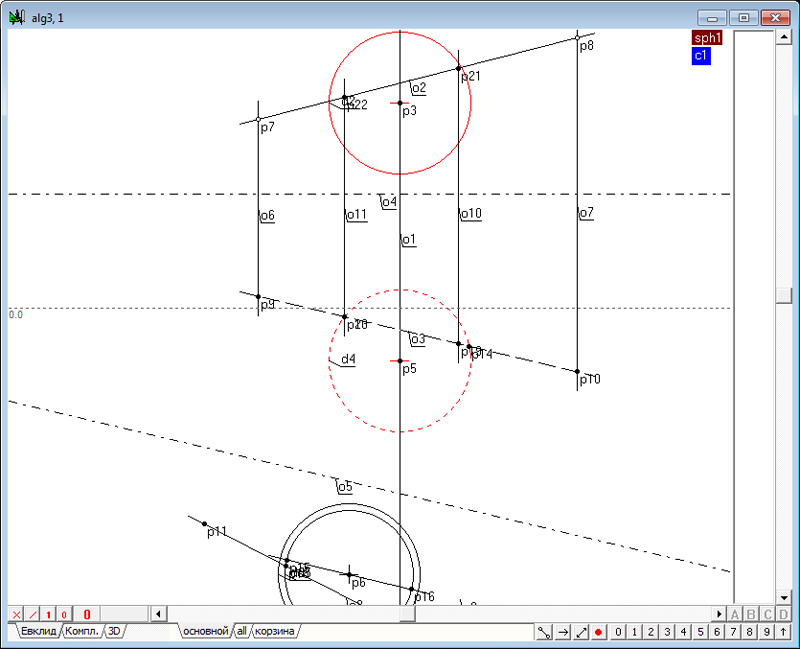
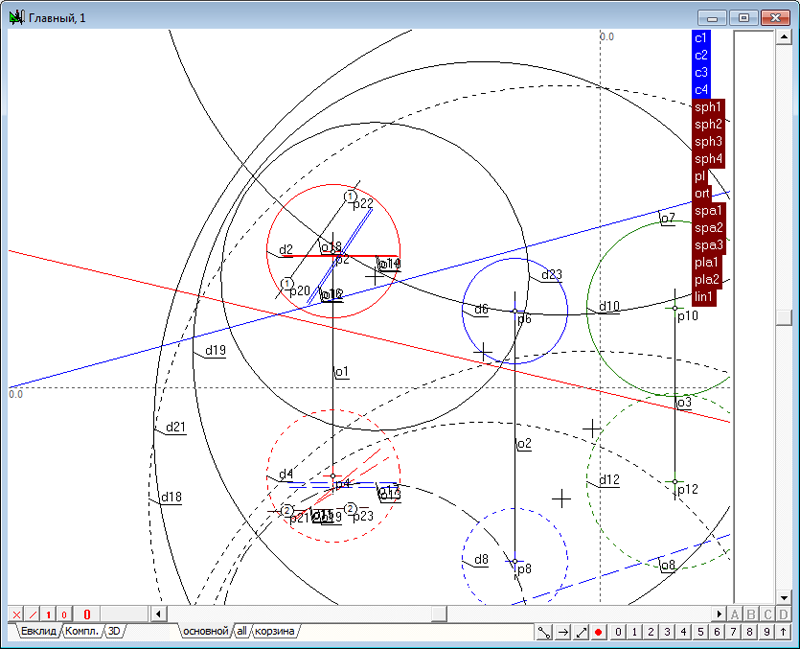
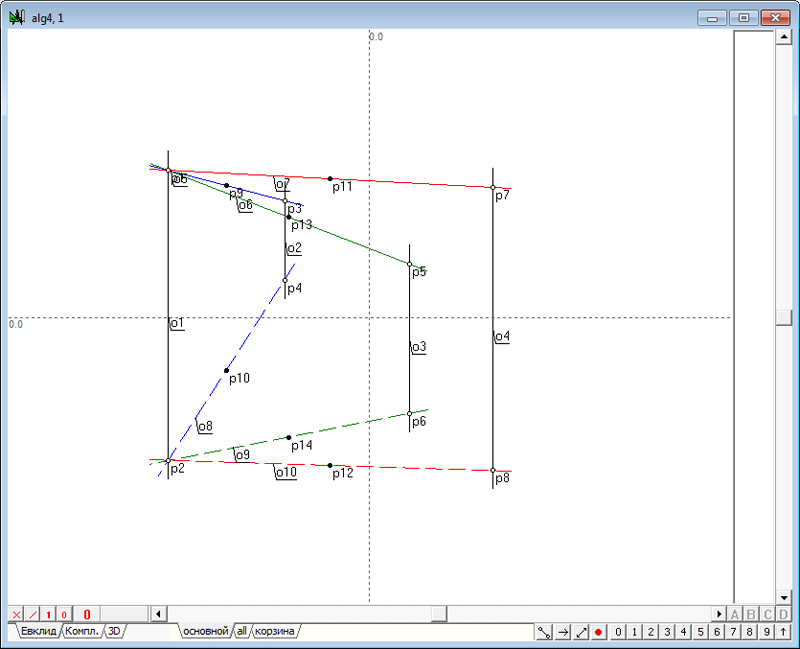
| 4 | Построим теперь касательные к окружностям в следующей последовательности: Выделим, удерживая нажатой клавишу Shift, красную и синюю окружности, изображающие фронтальные очерки первой и второй сферы. Нажав последовательно на клавиатуре клавиши o и 8, получим две линии касательные к красной и синей окружностям.
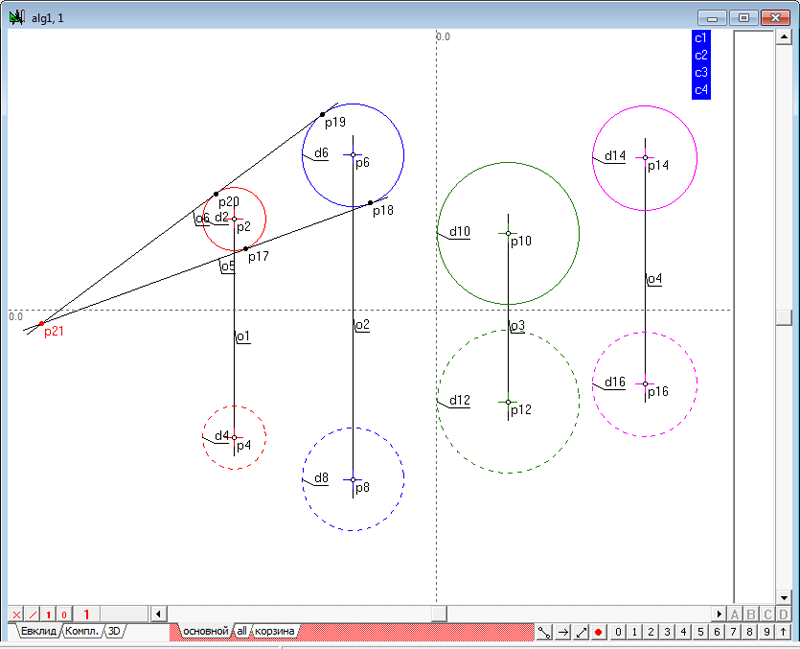
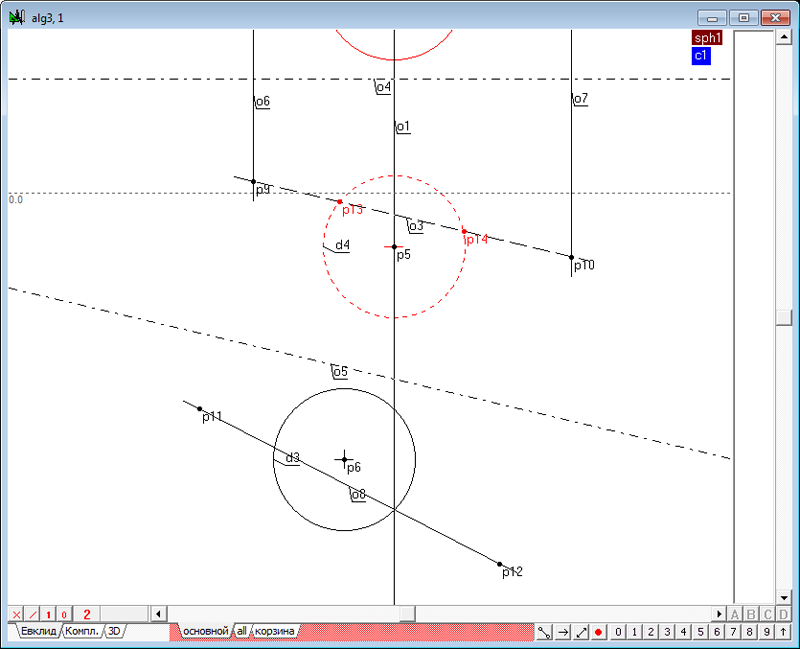
Рис. 3 Обе касательные прямые o5 и o6 выделены, поэтому, нажав на клавиатуре клавишу с латинским символом p, получим точку пересечения касательных - центр подобия p21 двух окружностей d2 и d6.
Рис. 4 |
||
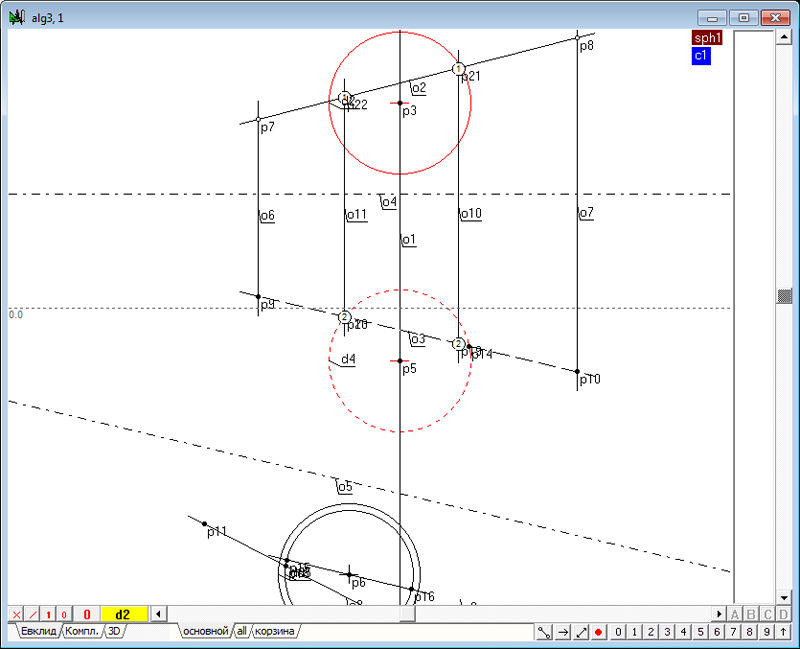
| 5 | Комбинацией клавиш Alt+1 пометим выделенную точку p21 значком, поясняющим, что эта точка относится к первой проекции модели.
Рис. 5 |
||
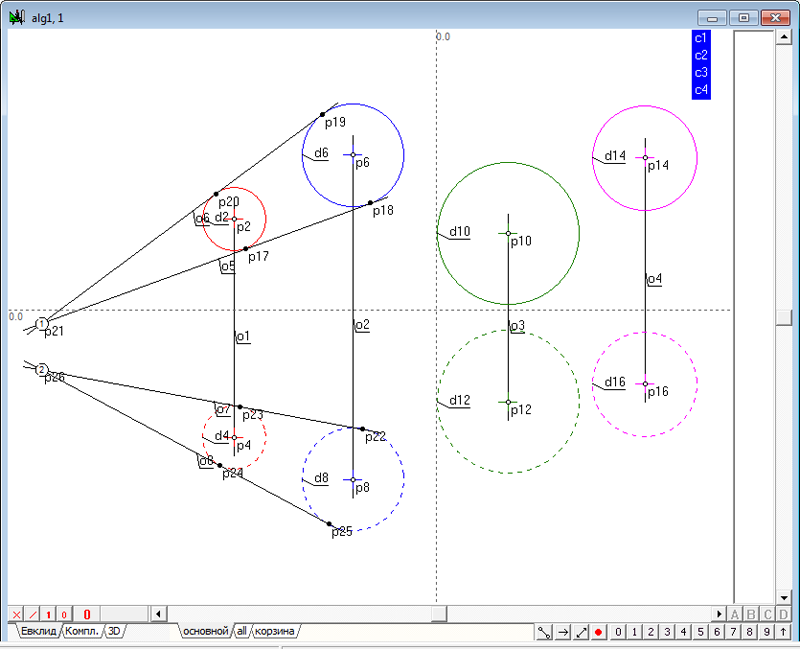
| 6 | Аналогичное построение выполним и в отношении окружностей d4, d8.
Рис. 16 Заметим, что точки p21, p26 находятся на одной линии связи и поэтому моделируют пространственную точку. |
||
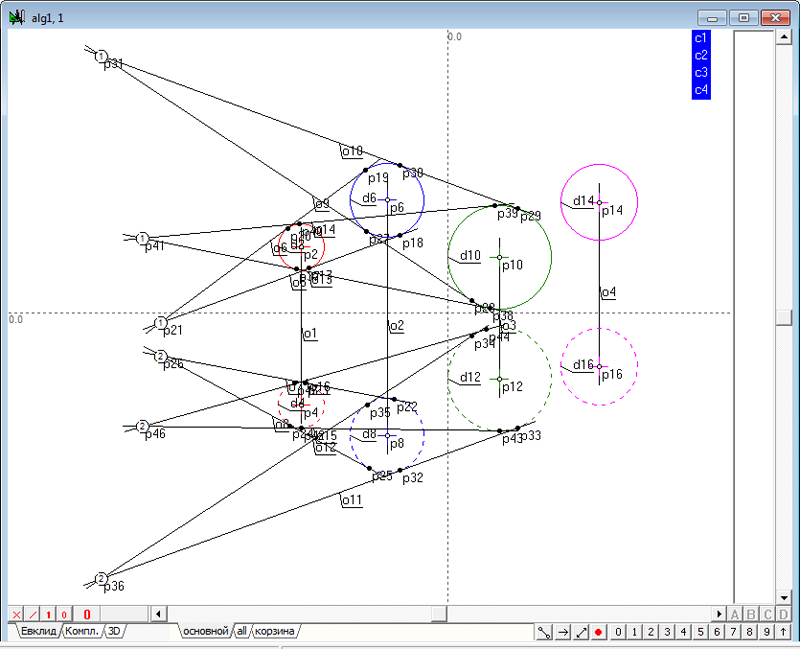
| 7 | Выполним те же построения в отношении пар окружностей d6-d10 и d8-d12, а также пар d2-d10 и d4-d12. Точки первого поля проекций p21, p31 и p41 находятся на одной прямой. Точки первого поля проекций p26, p36 и p46 также находятся на одной прямой.
Рис. 7 |
||
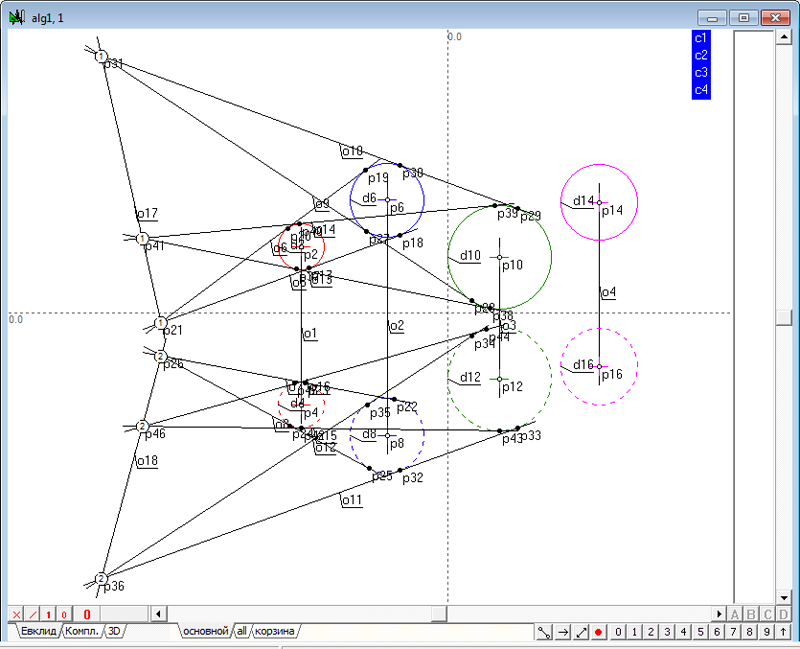
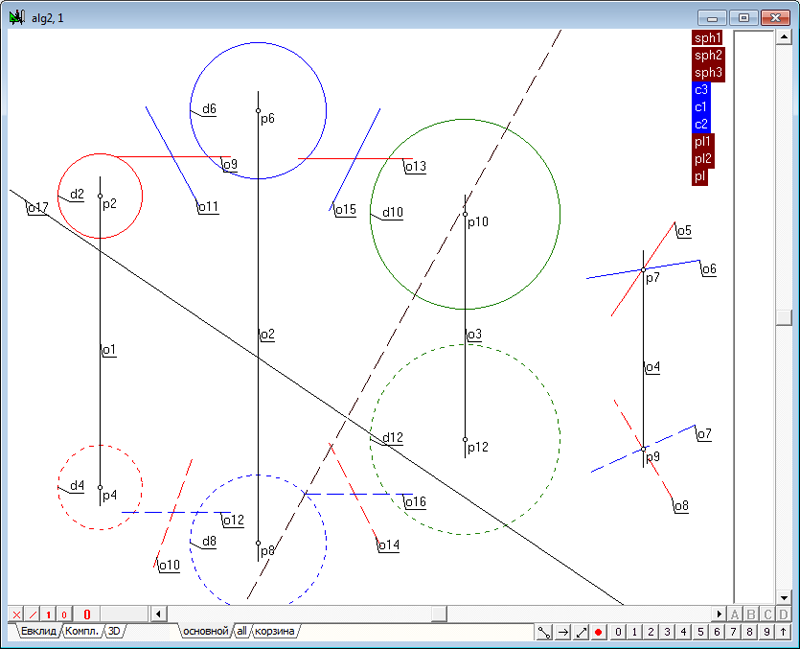
| 8 | Проведем через тройки точек прямые o 17 и o18.
Рис. 8 Обе эти прямые моделируют ось подобия тройки сфер - красной, синей и зеленой. |
||
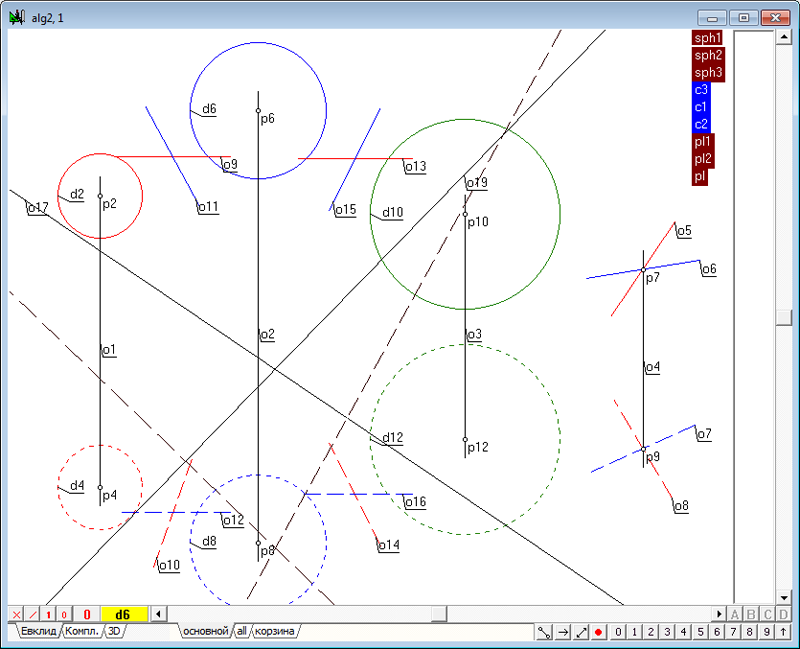
| 9 | Выбрав в качестве второй тройки сфер синюю, зеленую и фиолетовую сферы, получим еще одну радикальную ось, причем, поскольку одна пара сфер в обеих тройках общая (синяя-зеленая), то обе радикальные оси будут пересекаться в одной точке (p31-p36), определяя тем самым плоскость подобия четырех сфер.
Рис. 9 |
||
| 10 | Выделим цветом и признаками начертания выходные параметры алгоритма. Выделим последовательно прямые o17, o18, o27 и o28 и, вызвав правой кнопкой мыши контекстное меню, выберем пункт Назначить o17, o18, o27, o28 выходом алгоритма. Затем выделим последовательно окружности, моделирующие сферы, в следующей последовательности: d2, d4, d6, d8, d10, d12, d14, d16 и, вызвав правой кнопкой мыши контекстное меню, выберем пункт Назначить d2, d4, d6, d8, d10, d12, d14, d16 входом алгоритма.
Рис. 10 |
||
| 11 | Вызовем диалоговое окно для формирования интерфейса алгоритма комбинацией клавиш Alt+A. Укажем названия входных и выходных параметров Для d2: 1-я проекция 1-й сферы; Для o17: 1-я проекция 1-й прямой плоскости; Укажем название алгоритма - Плоскость подобия четырех сфер. На этом создание алгоритма можно считать завершенным, а окно, в котором выполнялось построение, можно закрыть. |
||
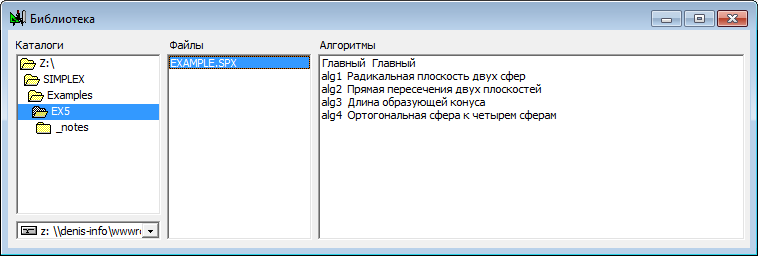
| 12 | Для решения задачи нам потребуется алгоритм построения сферы, ортогональной к четырем другим сферам. Разумеется, такой алгоритм можно реализовать в проекте "с нуля". Однако, можно пойти и другим путем - воспользоваться результатом работы, выполненной ранее, если вспомнить, что такой алгоритм уже был разработан и использован в проекте прошлого примера. Для этого вызовем командой Библиотека основного меню Файл диалоговое окно импорта алгоритмов в текущий проект. Предварительно нужно, конечно, позаботиться о том, чтобы требуемый файл с алгоритмом был загружен и размещен где-либо на носителе информации. Указав в диалоговом окне путь к файлу и сам файл, получим в списке Алгоритмы перечень всех алгоритмов, реализованных в проекте этого файла. Среди них, в частности, имеется алгоритм с именем alg4 и названием Ортогональная сфера к четырем сферам, который необходим для решения нашей текущей задачи.
Рис. 11 |
||
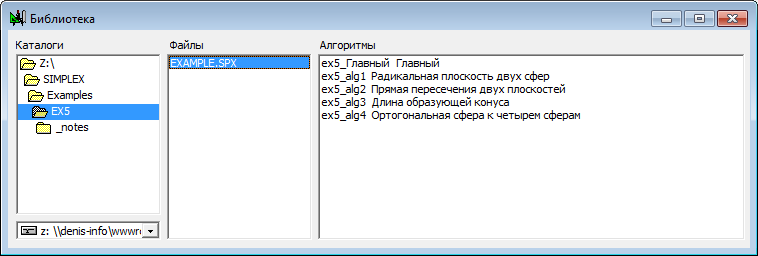
| 13 | Следует обратить внимание на то, что и в текущем проекте и в проекте-"доноре" имена алгоритмов могут совпадать, поскольку при создании алгоритмов система автоматически генерирует их имена на основе префикса alg. Поэтому простое копирование алгоритма (и, возможно, всех необходимых для его исполнения алгоритмов, на которые он ссылается) и привнесение его в новый проект может привести к конфликту имен алгоритмов, поскольку они могут совпадать. Поэтому следует позаботиться о том, чтобы переименовать алгоритмы таким образом, чтобы избежать конфликта имен. Для этого щелчком правой кнопки мыши над списком Алгоритмы диалоговой панели Библиотека вызовем контекстное меню и выберем пункт Переименовать. В результате перед нами появится поле ввода префикса имени, который будет подставлен перед именами всех алгоритмов алгоритма-"донора" перед привнесение этих алгоритмов в текущий проект. Изначально префикс будет совпадать с именем файла, в котором содержится данный проект, в частности префикс EXAMPLE. Изменим его, например, на другой префикс - ex5.
Рис. 12 После нажатия на кнопку OK система представит нам список алгоритмов с измененными именами, причем следует заметить, что эти изменения будут учтены и при возможных обращениях одних алгоритмов к другим алгоритмам. Однако эти изменения не оказывают никакого влияния на сам проект, из которого импортируются алгоритмы - содержимое его файла не подвергается никаким изменениям.
Рис. 13 Теперь, вызвав контекстное меню, выполним копирование в буфер Clipboard алгоритма с названием Ортогональная сфера к четырем сферам и, возможно, всех тех алгоритмов, которые необходимы для его функционирования. Поиск таких зависимостей осуществляется автоматически и не требует каких-либо усилий и внимания со стороны пользователя.
Рис. 14 Теперь нужно осуществить вставку содержимого буфера Clipboard в текущий проект. Для этого вызовем контекстное меню над каким-либо из имеющихся окон реализации алгоритма в нашем проекте и выберем пункт Вставить.
Рис. 15 В появившемся диалоговом окне, предназначенном для указания конкретного способа вставки содержимого буфера Clipboard в проект выберем способ Обыкновенная вставка и нажмем на кнопку Вставить.
Рис. 16 Это действие, однако, не приведет к каким-либо видимым изменениям. Для того чтобы удостовериться в том, что все выполнено правильно, обратимся к диалоговому окну назначения связи алгоритма проекта с рабочим окном, используя комбинацию клавиш Ctrl+L.
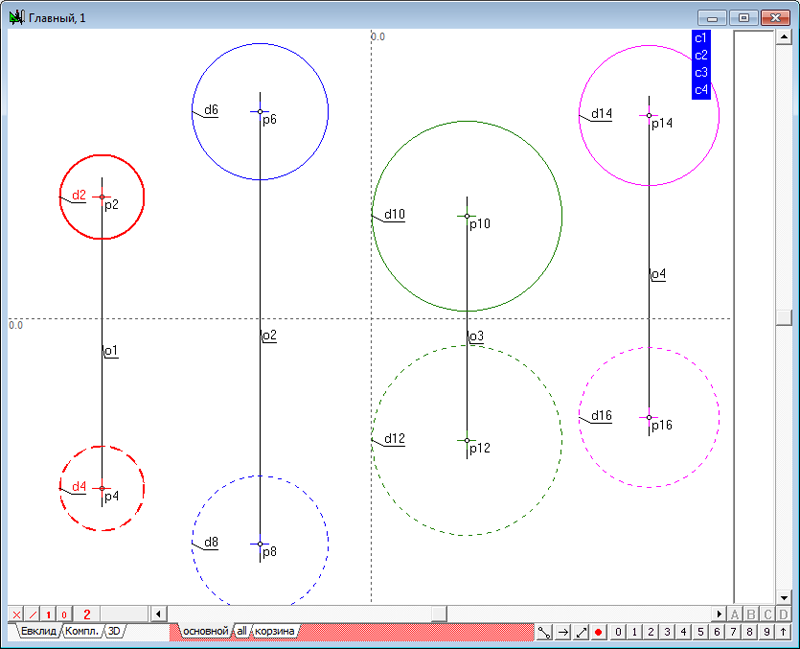
Рис. 17 Теперь мы можем убедиться в том, что проект пополнился не только алгоритмом с названием Ортогональная сфера к четырем сферам, но и сопутствующими алгоритмами, необходимыми для его работы. Причем все эти алгоритмы были привнесены в текущий проект автоматически без необходимости каких-либо дополнительных действий и внимания со стороны пользователя. Для обеспечения большего удобства при работе с данными, представляющими пространственные объекты, в частности, сферы, плоскости и прямые линии, будет целесообразно организовать именованные группы, объединяющих в себе по смыслу те данные, которые моделируют эти объекты. Так, например, выделив, удерживая нажатой клавишу Shift, окружности d2 и d4, моделирующие первую исходную сферу, создадим для них группу. Для этого на клавиатуре следует нажать на клавишу с латинским символом G (верхний регистр).
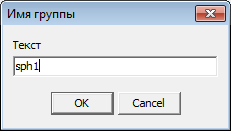
Рис. 18 В результате перед нами появится окно с именем группы, предлагаемой системой по умолчанию. Для того чтобы было легче различать группы, изменим это имя на более смысловое, например, на имя sph1, устанавливающее ассоциацию с первой исходной сферой.
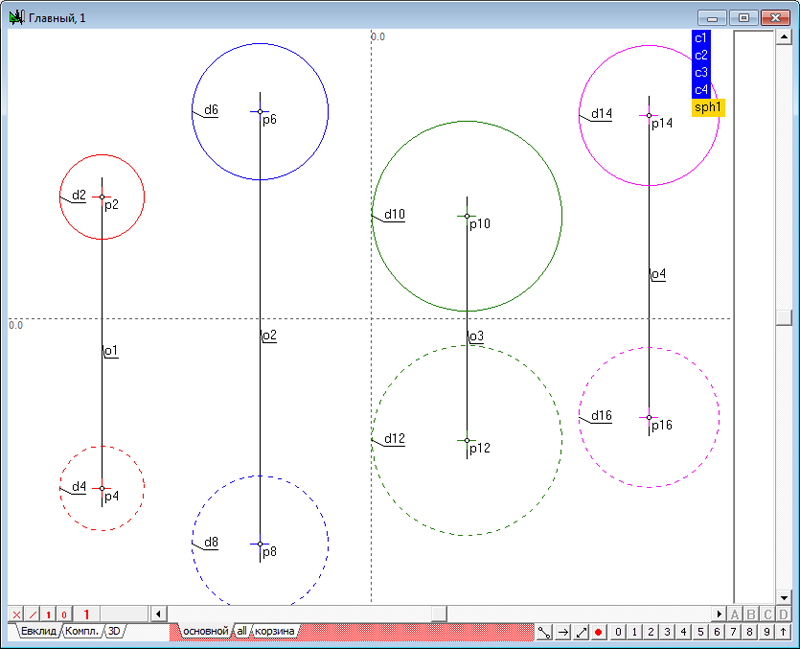
Рис. 19 После нажатия на кнопку OK, к меткам имен на правой стороне окна будет добавлена метка группы с именем sph1,
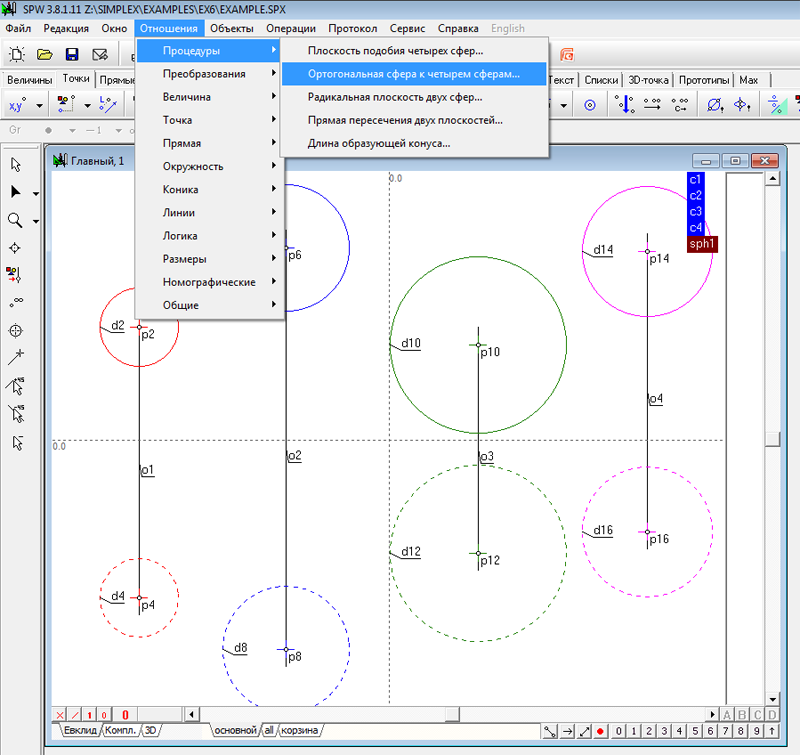
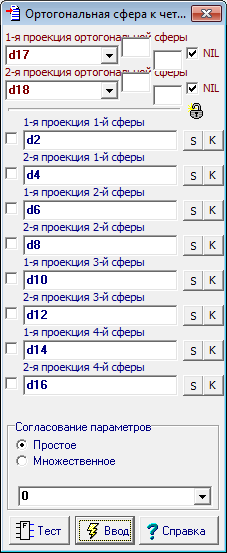
Рис. 20 Аналогичным образом создадим группы для всех остальных сфер, задав им имена sph2 - sph4. Теперь можно построить сферу, проходящую ортогонально к четырем заданным сферам. Выбрав пункт меню Отношения/Процедуры/Ортогональная сфера к четырем сферам... вызовем диалоговую панель для формирования параметров соответственной команды.
Рис. 21 |
||
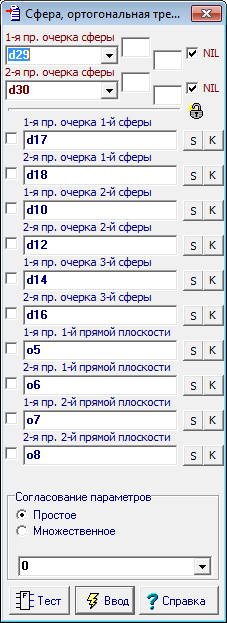
| 14 | Безусловно, все поля этой панели можно заполнить, указывая курсором мыши на соответственные объекты. Однако такой способ требует от пользователя повышенного внимания и сопряжен с появлением непреднамеренных ошибок. Более удобным способом ввода параметров будет обращение к ссылкам групп, объединяющих в себе данные всех сфер. Поэтому при вводе команды щелкнем девой кнопкой мыши над метками sph1, sph2, sph3 и sph4, в результате чего все текстовые поля диалоговой панели будут корректно заполнены необходимыми данными.
Рис. 22 |
||
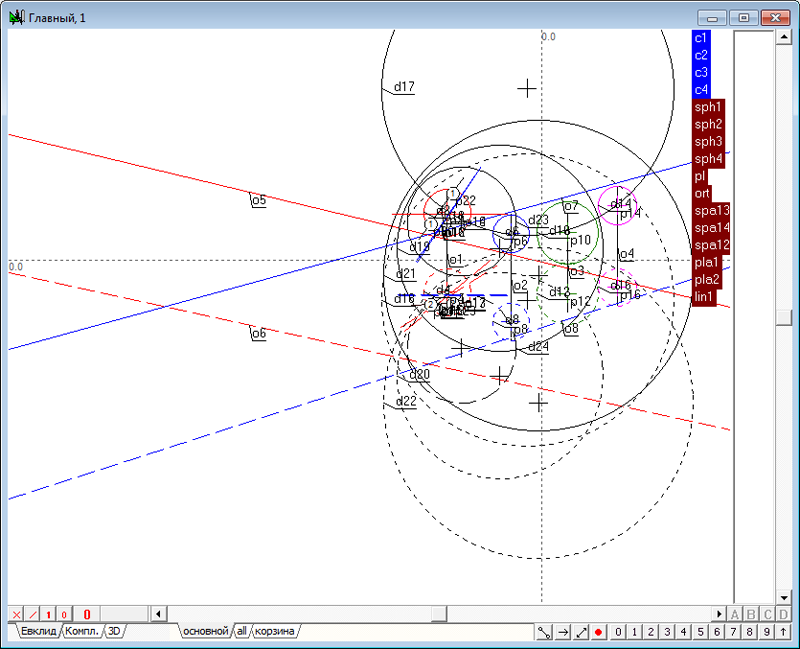
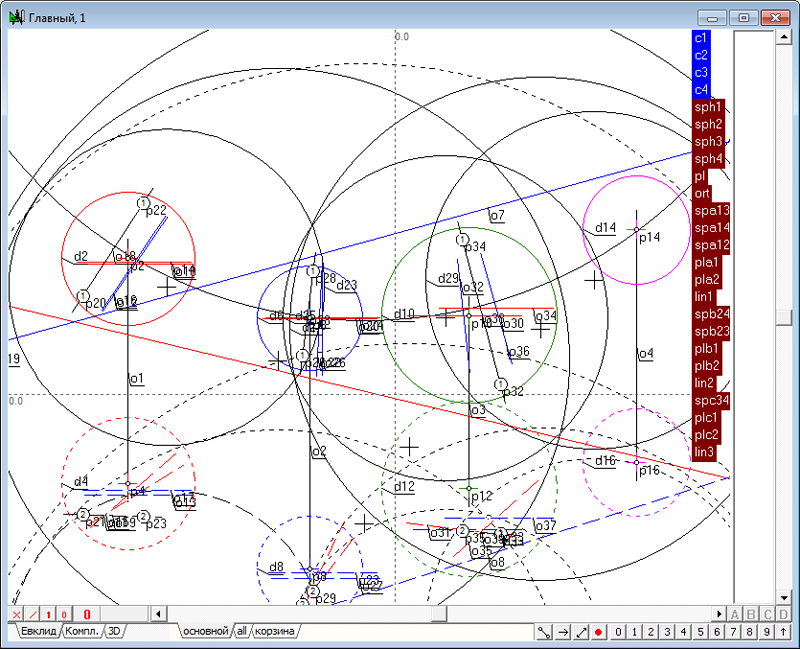
| 15 | После нажатия на кнопку OK диалоговой панели ввода команды в окне реализации алгоритма будет построена модель ортогональной сферы - две окружности d17 и d18. Создадим группу для построенной сферы, выделив окружности d17 и d18 и нажав на клавиатуре клавишу с символом G. Дадим название группе - ort.
Рис. 23 |
||
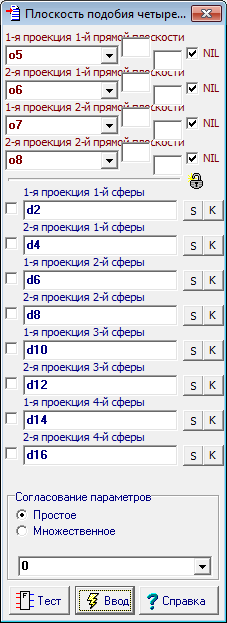
| 16 | Аналогичным образом построим теперь и модель плоскости подобия четырех сфер, вызвав соответственную команду из главного меню и сославшись на имена групп с данными сфер.
Рис. 24 |
||
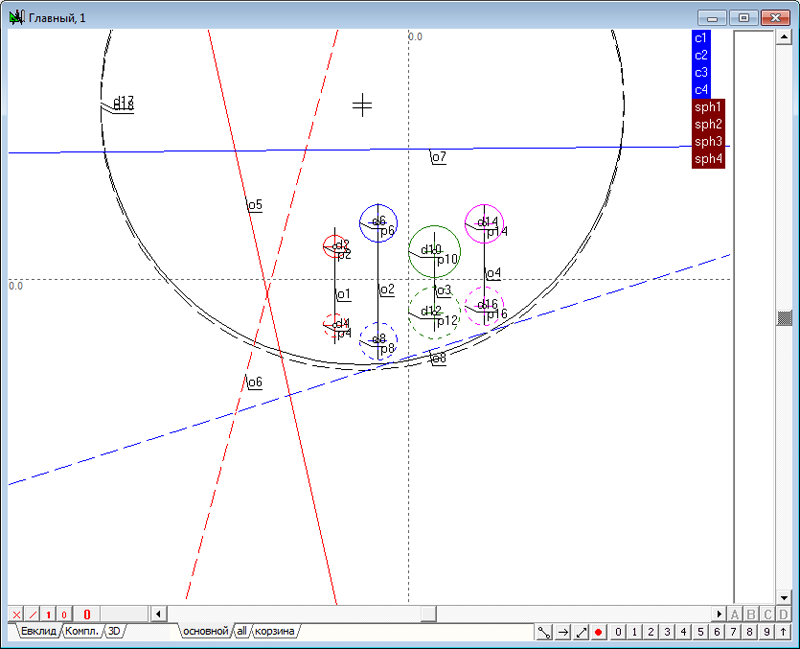
| 17 | На экране будут отображены четыре прямые линии, моделирующие плоскость подобия.
Рис. 25 |
||
| 18 | Так же, как и в случае сфер, эту данные этой плоскости целесообразно организовать в группу. Поэтому, последовательно выделив первую проекцию первой линии (например, сплошную красную линию), вторую проекцию первой линии (штриховую красную линию), затем первую проекцию второй линии (сплошную синюю линию) и вторую проекцию второй линии (штриховую синюю линию), нажмем на клавиатуре клавишу с символом G и укажем имя группы, например, pl. Для дальнейшего решения задачи нам потребуется создать алгоритм, который позволит строить сферу, ортогональную к трем сферам и плоскости. Поскольку в этом алгоритме в качестве исходных данных нам будут необходимы модели трех сфер, то скопируем уже имеющиеся сферы из текущего алгоритма в буфер Clipboard. Для этого выделим метки групп sph1, sph2 и sph3 и нажмем на клавиатуре комбинацию клавиш Ctrl+C.
Рис. 26 |
||
| 19 | В появляющихся в результате этого действия диалоговых окнах выберем способ копирования С предками и выделим все объекты, представленные в окне Захват.
Рис. 27 |
||
| 20 | Создадим новый алгоритм комбинацией клавиш Ctrl+Alt+N и вставим в него содержимое буфера Clipboard командой Ctrl+V.
Рис. 28 |
||
| 21 | Сформируем модель плоскости.
Рис. 29 |
||
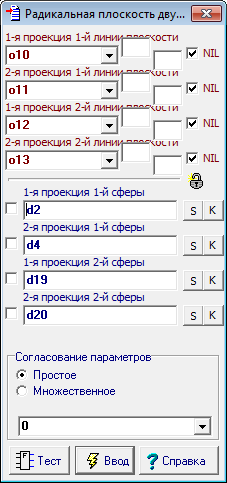
| 22 | Создадим группу для данных плоскости, включив в нее прямые линии o5, o8, o6 и o7. Назовем группу pl. Вызовем команду построения радикальных плоскостей и, ссылаясь на группы сфер sph1-sph2, sph2-sph3 построим две соответственные радикальные плоскости. Объединим данные этих плоскостей в группы pl1 и pl2.
Рис. 30 |
||
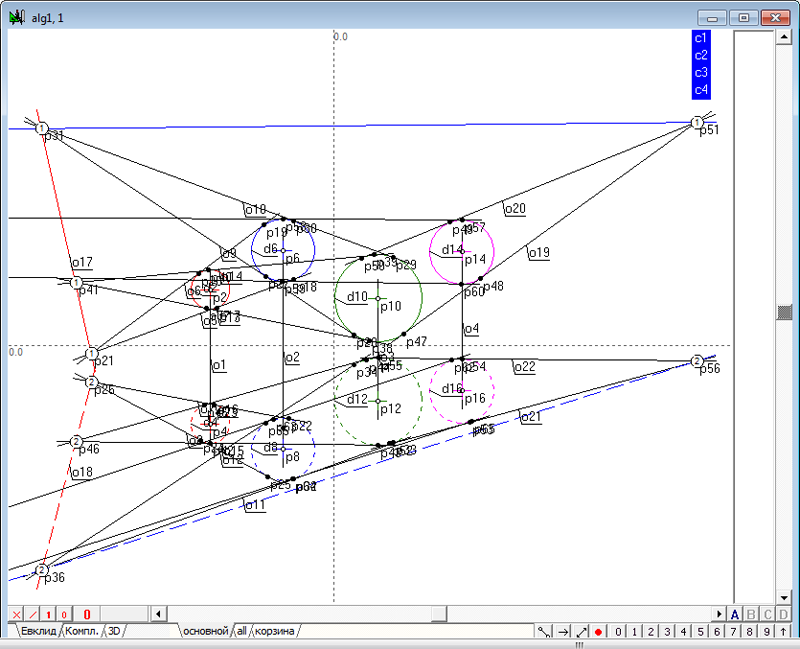
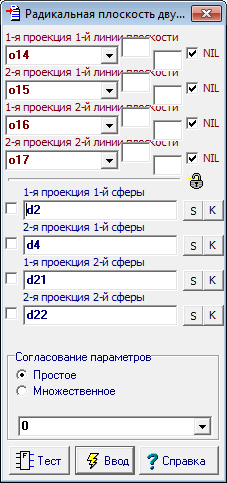
| 23 | Выполним команду пересечения плоскостей pl1 и pl2.
Рис. 31 |
||
| 24 | Получим модель линии пересечения o17-o18.
Рис. 32 |
||
| 25 | Аналогичным образом найдем линию пересечения плоскости pl2 и pl - прямые o19, o20.
Рис. 33 |
||
| 26 |
Рис. 33 |
||
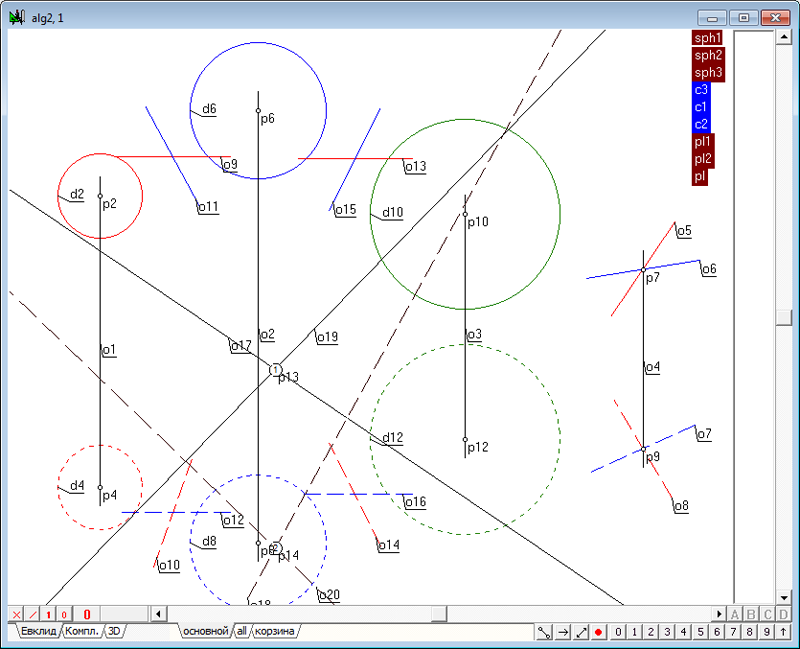
| 27 | Дважды выполнив функцию пересечения прямых (o17,o19) и (o18,o20) найдем точки p13 и p14, моделирующие центр сферы, ортогональной к исходным объектам. Выделим точку p13 и нажмем комбинацию клавиш Alt+1, для того чтобы пометить эту точку знаком первого поля проекций. Аналогично выделим точку p13 и нажмем комбинацию клавиш Alt+2, для того чтобы пометить эту точку знаком второго поля проекций.
Рис. 34 |
||
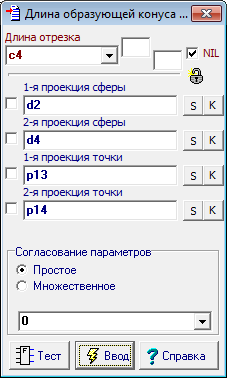
| 28 | Для определения радиуса ортогональной сферы воспользуемся функцией, привнесенной проекта-"донора" Длина образующей конуса с вершиной в точке p13-p14, опущенного на сферу с очерками d2-d4. Искомое расстояние будет содержаться в переменной c4.
Рис. 35 |
||
| 29 | Построим очерки сферы, ортогональной к исходным объектам. Для этого выделим последовательно, удерживая нажатой клавишу Shift, точку p13 и метку величины c4, после чего нажмем на клавиатуре клавишу с символом d. В результате будет получена окружность d7. Затем выделим последовательно, удерживая нажатой клавишу Shift, точку p14 и метку величины c4, после чего нажмем на клавиатуре клавишу с символом d. Получим окружность d9. Изменим атрибут ее начертания на штриховое, для того чтобы было легче отличать ее от линии, моделирующей первую проекцию очерка сферы.
Рис. 36 |
||
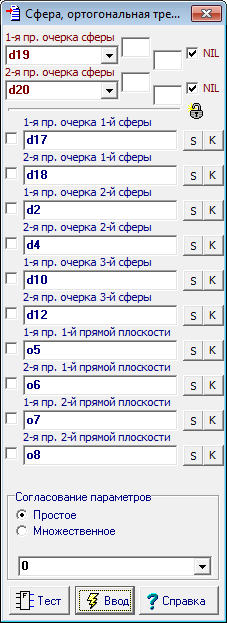
| 30 | Теперь выделим последовательно объекты, моделирующие входные параметры алгоритма и вызовем из контекстного меню окна команду назначения этих объектов в качестве входных параметров алгоритма. В появляющихся диалоговых окнах присвоения названий соответственным параметрам, укажем следующие названия: 1-я пр. очерка 1-й сферы; Выделим окружности d7 и d9 и назначим их в качестве выходных параметров алгоритма соответственной командой контекстного меню. В появляющихся диалоговых окнах присвоения названий соответственным параметрам, укажем следующие названия: 1-я пр. очерка сферы; Вызвав диалоговое окно назначения параметров алгоритма комбинацией клавиш Alt+A, укажем название сформированного алгоритма: Сфера, ортогональная к трем сферам и плоскости. |
||
| 31 | Перейдем в основной алгоритм и построим сферу, ортогональную к сфере ort, к первой исходной сфере sph1, к сфере sph3 и плоскости подобия pl.
Рис. 37 Оформим группу spa1 для двух образованных окружностей. Рис. 38 |
||
| 32 | Построим сферу, ортогональную к сфере ort, к первой исходной сфере sph1, к сфере sph4 и плоскости подобия pl.
Рис. 39 Создадим группу spa2 для двух образованных окружностей. Рис. 40 |
||
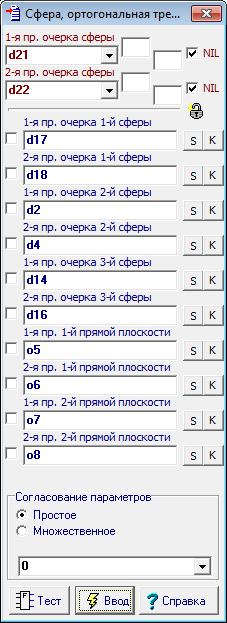
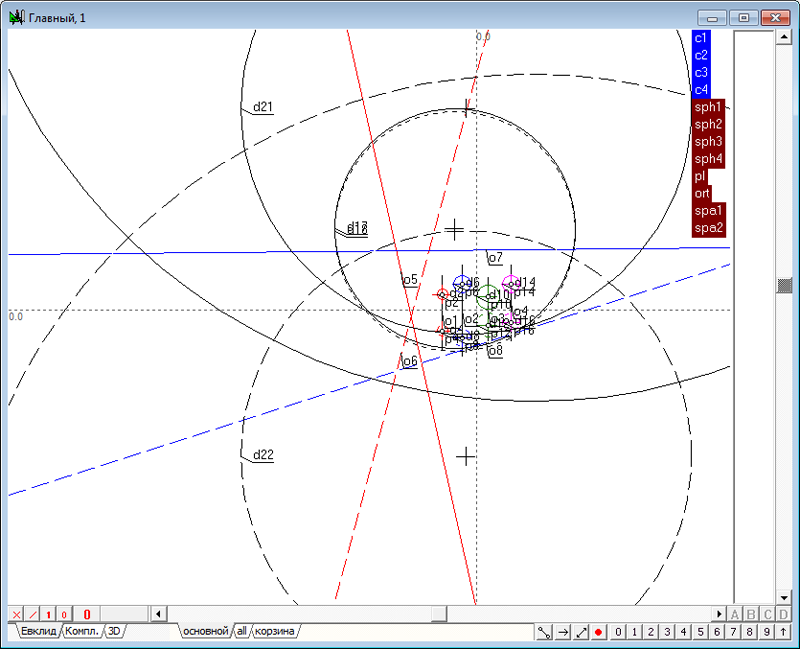
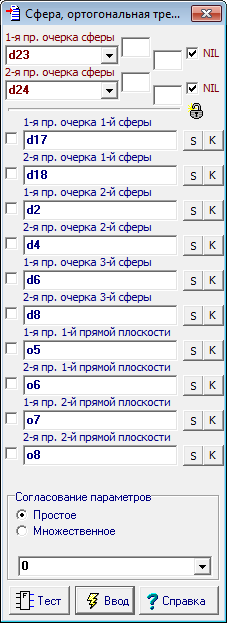
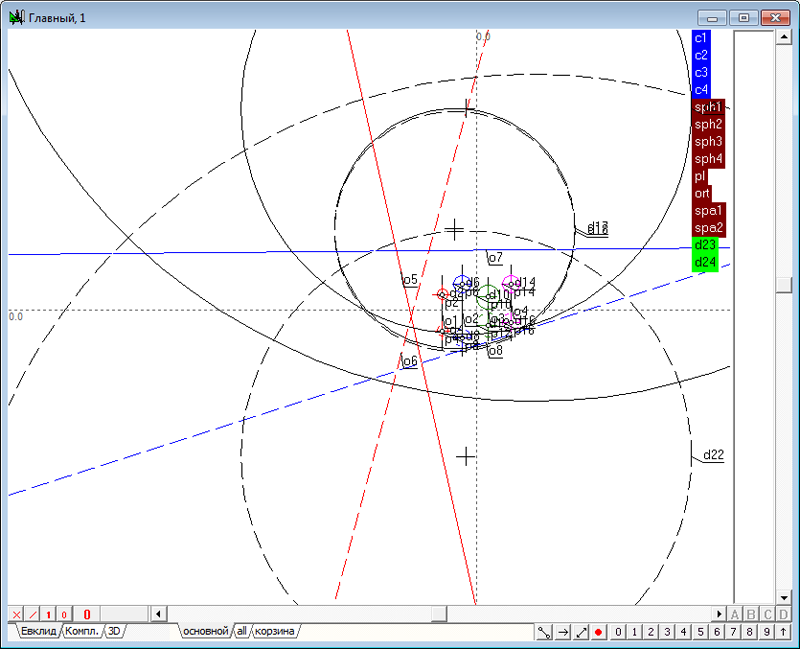
| 33 | Построим сферу, ортогональную к сфере ort, к первой исходной сфере sph1, к сфере sph2 и плоскости подобия pl.
Рис. 41 В результате выполненного построения объекты d23 и d24 оказались нерассчитанными. Такая ситуация может возникнуть, например, в случае вырождения геометрического построения или в случае неправильной реализации того или иного алгоритма, участвующего в построении. Вопросы отладки и устранения ошибок, которые обычно сопровождают процесс решения задачи, в данном руководстве мы рассматривать не будем.
Рис. 42 |
||
| 34 | Попытаемся слегка изменить положение исходных сфер шейпером, для того чтобы устранить возникшее вырождение геометрического построения. В частности, изменив незначительно положение линии связи, соединяющей центры сферы sph1 и радиус окружностей, моделирующих очерк этой сферы, нам удается избежать вырождения в проектируемом алгоритме. Оформим группу spa3 для двух образованных окружностей.
Рис.43 |
||
| 35 | Найдем теперь радикальную плоскость, образованную первой исходной сферой sph1 и сферой spa1.
Рис. 44 Оформим группу pla1 для образовавшихся прямых. Для формирования такой группы нажмем комбинацию клавиш Alt+F12. При этом только что образованные объекты будут автоматически выделены, а на экране появится диалоговая панель с предложением указать имя группы, назначаемой выделенным объектам. Укажем в этом окне имя pla1.
Рис. 45 |
||
| 36 | Найдем теперь радикальную плоскость, образованную первой исходной сферой sph1 и сферой spa2.
Рис. 46 Оформим группу pla2 для образовавшихся прямых. Для формирования такой группы нажмем комбинацию клавиш Alt+F12. Укажем в появившемся окне имя pla2. Рис.47 |
||
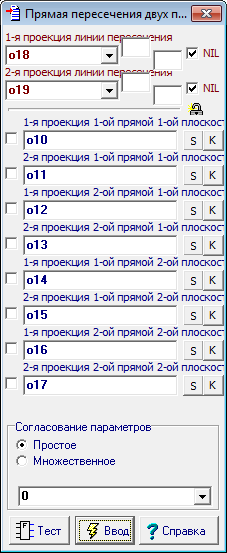
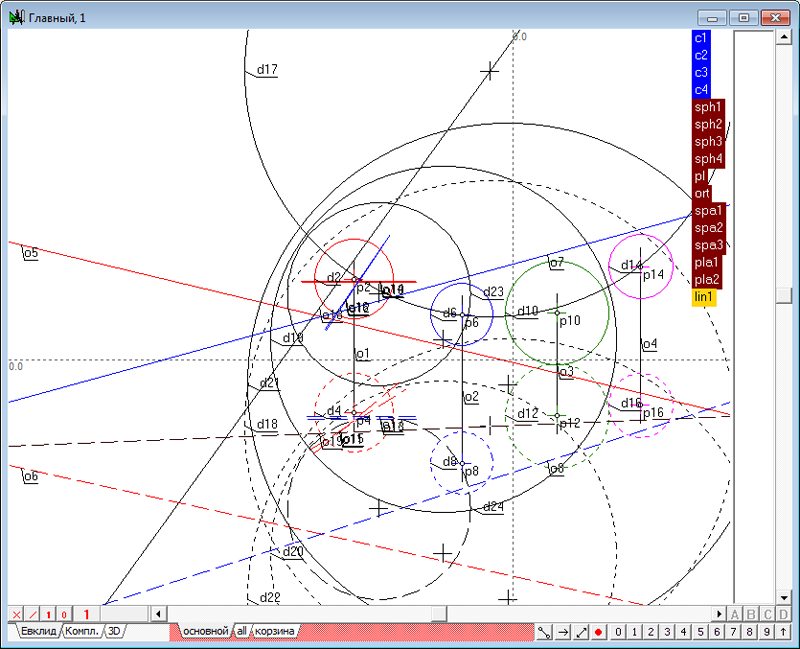
| 37 | В принципе, можно было бы построить и третью радикальную плоскость, образованную сферами sph1 и spa3, однако в этом нет необходимости, так как все эти плоскости пересекаются по одной и той же прямой линии. Поэтому для построения такой линии нам будет достаточно наличие лишь двух плоскостей - pla1 и pla2. Найдем эту линию, воспользовавшись функцией Прямая пересечения двух плоскостей и, вызвав комбинацией клавиш Alt+F12 команду формирования группы из объектов последней исполненной операции, объединим эти объекты под именем lin1.
Рис. 48
Рис. 49 |
||
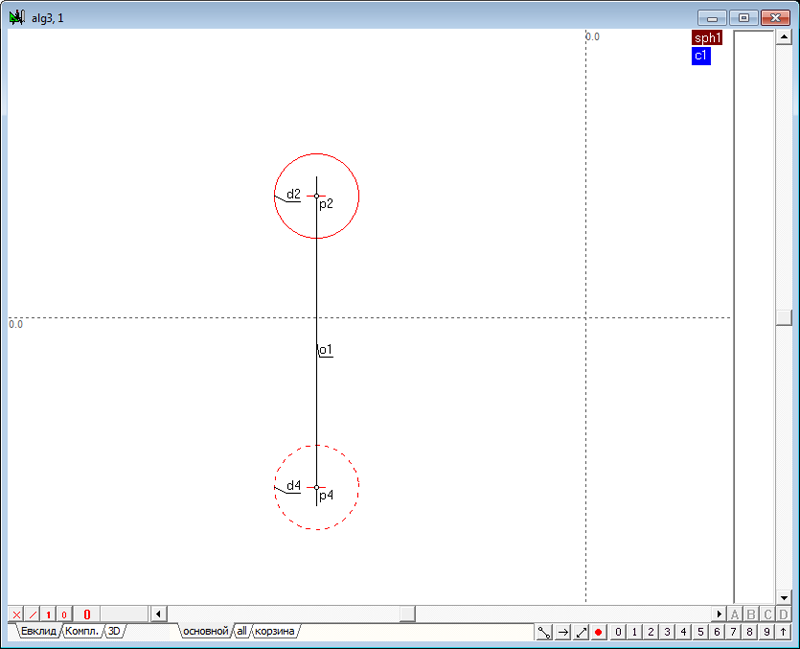
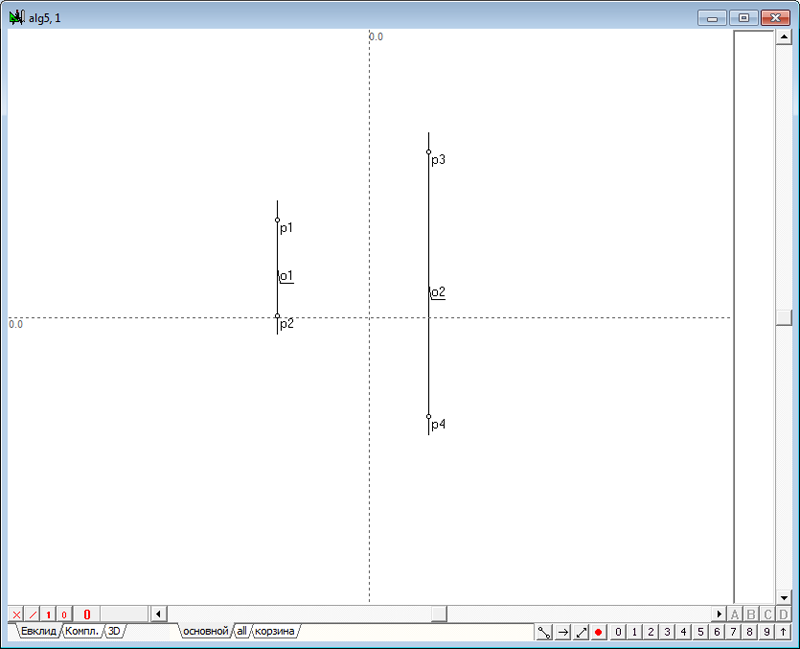
| 38 | Для нахождения точек касания искомых сфер с исходными сферами нам потребуется, в частности, найти точки пересечения найденной линии lin1 с первой исходной сферой sph1, а затем выполнить аналогичные действия с другими исходными сферами и соответственными им прямыми линиями, которые еще предстоит построить. Поэтому создадим еще один алгоритм, который будет отвечать за построение точек пересечения прямой линии и сферы, который нам предстоит применить в решаемой задаче четыре раза. Создадим новый алгоритм, используя для этого комбинацию клавиш Ctrl+Alt+N, и построим в нем любым доступным нам способом модель сферы.
Рис. 50 |
||
| 39 | Построим модель прямой линии.
Рис. 51 |
||
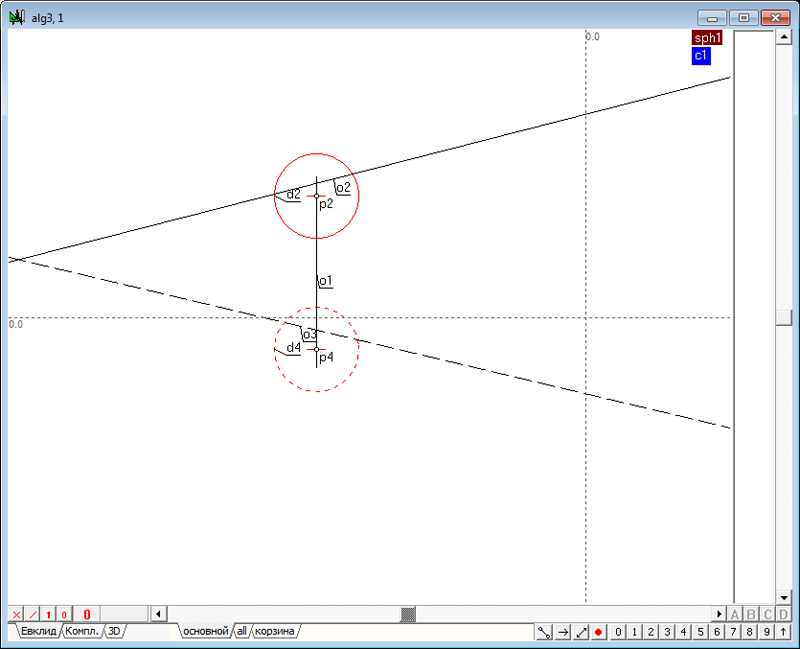
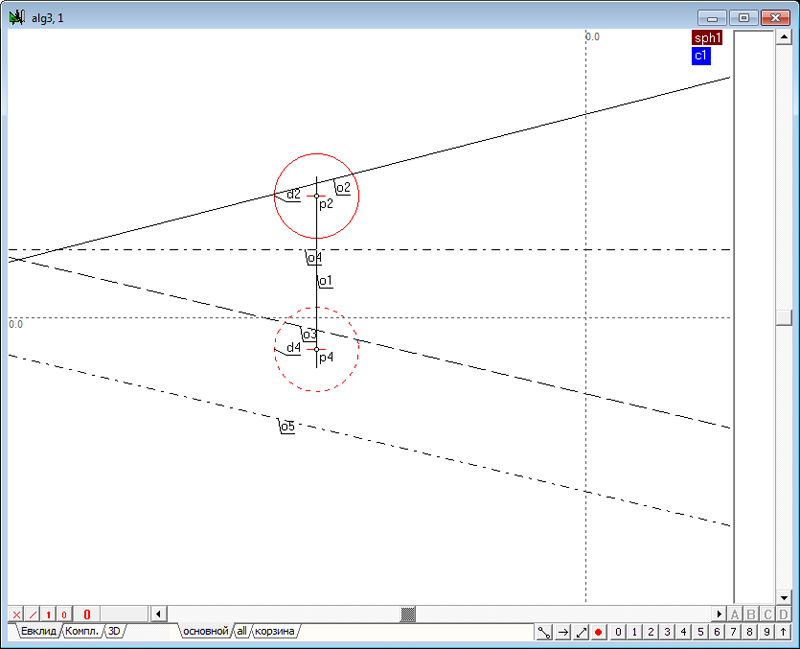
| 40 | В произвольном месте поля чертежа командой h зададим горизонтальную линию o4, а затем, выделив проекцию o3 и, отведя от нее курсор на некоторое расстояние, нажмем на клавиатуре клавишу o, чтобы построить прямую o5, параллельную линии o3.
Рис. 52 |
||
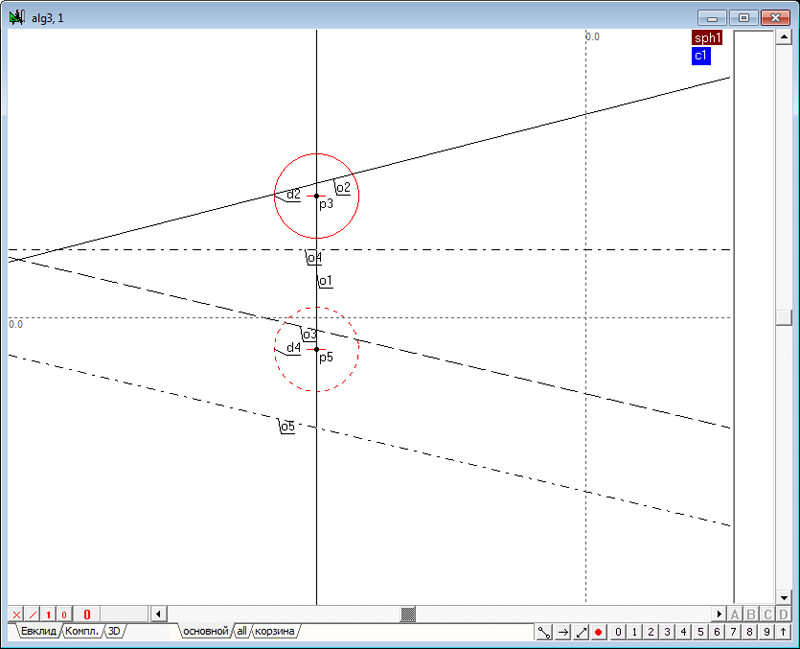
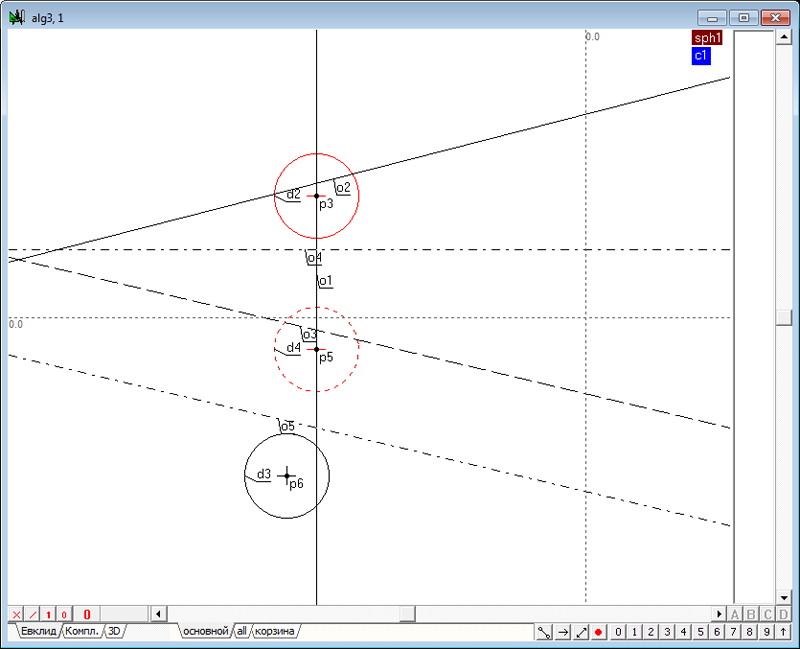
| 41 | Выделим точки p2 и p4 и перенесем их в слой корзина, нажав на клавиатуре клавишу \.
Восстановим положение центров окружностей (которые будут зависеть от этих окружностей), выделив объекты d2 и d4 и нажав на клавиатуре клавишу с латинским символом c. Рис. 54 |
||
| 42 | Воспользуемся функцией Точка в замене плоскостей проекций, для того чтобы построить очерк и центр сферы в третьем дополнительном поле.
Рис. 55 |
||
| 43 | Для перевода прямой линии в третье дополнительное поле, построим на первой проекции прямой (линии o2) две инцидентные с этой прямой точки. Для этого, удерживая нажатой клавишу Ctrl, щелкнем два раза левой кнопкой мыши, разместив предварительно курсор над изображением прямой o2 в двух различных местах.
Рис. 56 |
||
| 44 | Построим вторые проекции точек, инцидентных с пространственной прямой. Для этого выделим точки p7 и p8, нажмем на клавиатуре клавишу с символом v, в результате чего будут построены прямые линии o6 и o7. Затем, удерживая нажатой клавишу Shift, добавим к выделению прямую o3 и нажмем клавишу с символом p, в результате чего будут построены точки p9 и p10, представляющие собой вторые проекции точек, инцидентных с прямой линией.
Рис. 57 |
||
| 45 | Используя функцию Точка в замене плоскостей проекций, построим проекции найденных точек в третьем поле. и проведем через них прямую линию o8, выделив предварительно точки p11 и p12 и нажав на клавиатуре клавишу с символом o.
Рис. 58 |
||
| 46 | В системе полей проекций, объединяющих в себе второе и третье поле, моделируемая прямая линия является линией уровня. Если теперь провести через прямую линию проецирующую плоскость, перпендикулярную второй плоскости проекций, то во втором поле она выродится в линию, совпадающую с прямой o3, а в третьем поле эта плоскость рассечет сферу по окружности. Диаметр этой окружности можно легко определить, если найти точки пересечения прямой линии o3 с окружностью d4. Для этого выделим объекты o3 и d4 и нажмем на клавиатуре клавишу с латинским символом p.
Рис. 59 |
||
| 47 | Проведем через точку p6 прямую линию, параллельную оси o5. Для этого выделим последовательно точку p6, прямую линию o5 и нажмем на клавиатуре клавишу с латинским символом O (верхний регистр). Добавим к выделению точки p13 и p14 и спроецируем их на прямую o9, нажав на клавиатуре клавишу с символом p. Через найденные выделенные точки проведем окружность d5, используя для этого команду, вызываемую клавишей с символом D (верхний регистр). Найдем точки пересечения p16 и p17 прямой o8 и окружности d5, выделив o8 и d5 и нажав на клавиатуре клавишу с символом p. Проекции точек пересечения пространственной прямой и сферы в дополнительном поле найдены. Теперь нужно восстановить соответственные проекции во втором и первом полях проекций.
Рис. 60 |
||
| 48 | Спроецируем точки p16 и p17, добавив к выделению прямую o3 и нажав на клавиатуре клавишу с символом p - получим точки p19 и p20. Нажав на клавишу с символом v, построим из найденных точек линии связи с первым полем и, добавив к ним в выделение прямую o2 и нажав на клавишу с символом p, определим положение первых проекций точек пересечения прямой линии со сферы.
Рис. 61 |
||
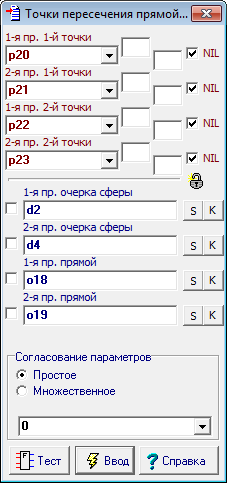
| 49 | Изменим атрибуты принадлежности найденных точек к соответственным полям проекций, выделяя их последовательно и используя для назначения атрибутов комбинации клавиш Alt+1 и Alt+2. Точки p21 и p22 будут отнесены к первому полю, а точки p19 и p20 - ко второму. Оформим интерфейс алгоритма (Alt+A), указав в качестве входных параметров исходные окружности и проекции прямой линии, а в качестве выходных параметров первые и вторые проекции двух точек пересечения прямой и сферы. Дадим название алгоритму - Tочки пересечения прямой и сферы.
Рис. 62 |
||
| 50 | Перейдя в Главный алгоритм, вызовем только что сформированную процедуру и, подставив во входные параметры диалоговой панели объекты, оформленные в виде групп sph1 и lin1 найдем искомые точки пересечения прямой линии lin1 и сферы sph1.
Рис. 63
Рис. 64 |
||
| 51 | Для удобства следующих построений имеет смысл переименовать сферы spa1, spa2 и spa3 таким образом, чтобы в их названиях отражались номера исходных сфер, которые являются дополнением к базовой исходной сфере и плоскости подобия, участвующих в операции. Переименуем группу spa1 в spa13, spa2 в spa14 и spa3 в spa12.
Рис. 65 |
||
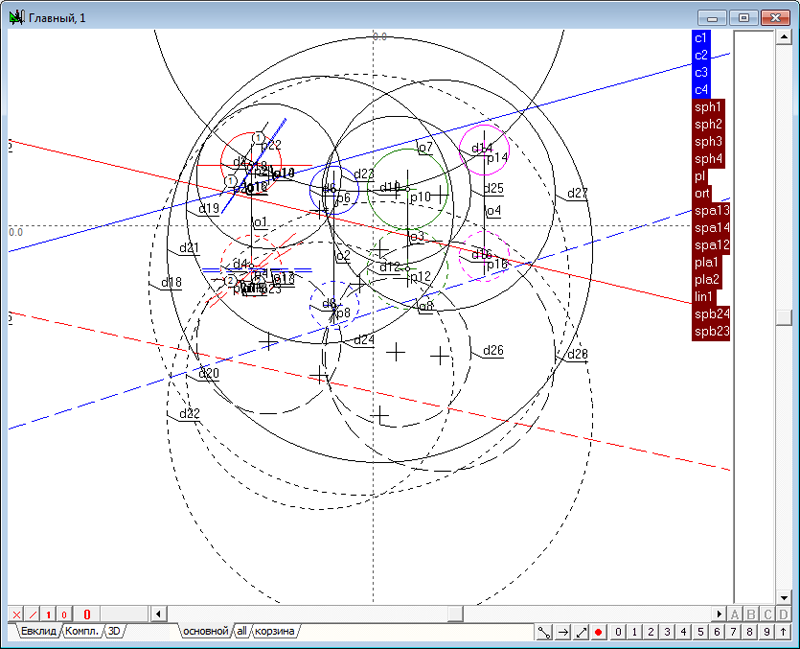
| 52 | Построим теперь две сферы, определенные на второй исходной сфере, плоскости подобия, а также третьей и четвертой исходных сферах соответственно. Объединим данные этих сфер в группы под именами spb24 и spb23. (Символом b обозначается ссылка на вторую исходную сферу, общую для обеих построенных). Построение сферы, наподобие spb21 не имеет смысла, так как она будет совпадать со сферой spa12, а таковая уже имеется в нашем распоряжении.
Рис. 66 |
||
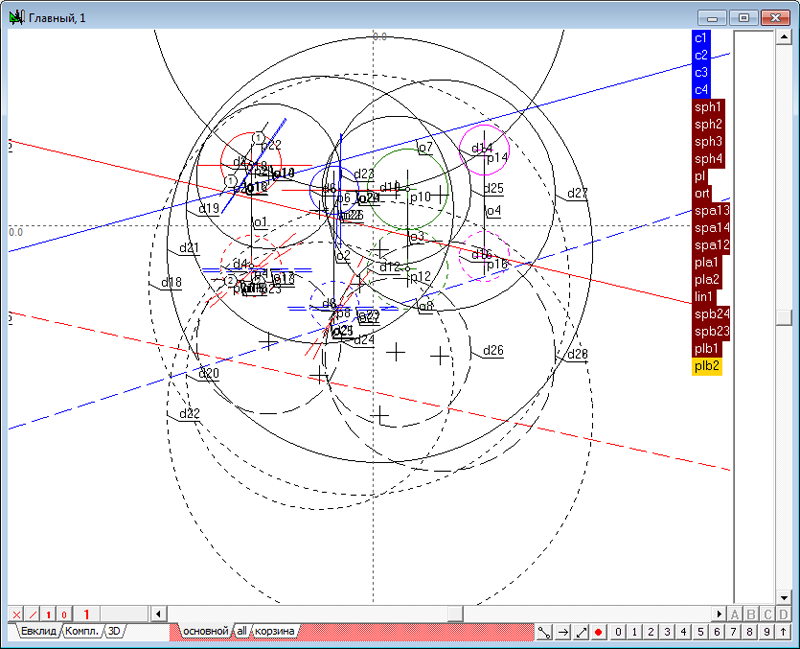
| 53 | Поэтому воспользуемся тремя сферами spa12, spb24 и spb23, относящимися ко второй базовой сфере, и построим две радикальные плоскости между второй исходной сферой и любыми двумя из ранее перечисленных. Оформим данные получаемых радикальных плоскостей в группы plb1 и plb2.
Рис. 67 |
||
| 54 | Найдем пересечение плоскостей plb1 и plb2 с формированием группы линии пересечения - lin2.
Рис. 68 |
||
| 55 | Найдем точки пересечения линии lin2 со второй исходной сферой.
Рис. 69 |
||
| 56 | По аналогии с предыдущим шагами построения, найдем сферу spc34. Две сферы, использующей для своего образования в качестве базовой третью исходную сферу, spa13 и spb23 уже имеются в нашем распоряжении.
Рис. 70 Построим радикальные плоскости plc1, plc2, линию lin3 и точки пересечения прямой lin3 со сферой sph3.
Рис. 71 |
||
| 57 | Аналогичные операции произведем для построения точек на четвертой исходной сфере.
Рис. 72 |
||
| 58 | Итак, точки касания двух сфер к четырем исходным найдены. Для решения оставшейся части задачи требуется разработать алгоритм построения сферы, проходящей через четыре заданные точки. Реализуем его. Откроем окно нового алгоритма комбинацией клавиш Ctrl+Alt+N и сформируем в нем модели четырех точек.
Рис. 73 |
||
| 59 | Соединим точки прямыми линиями и найдем их центры.
Рис. 74 |
||
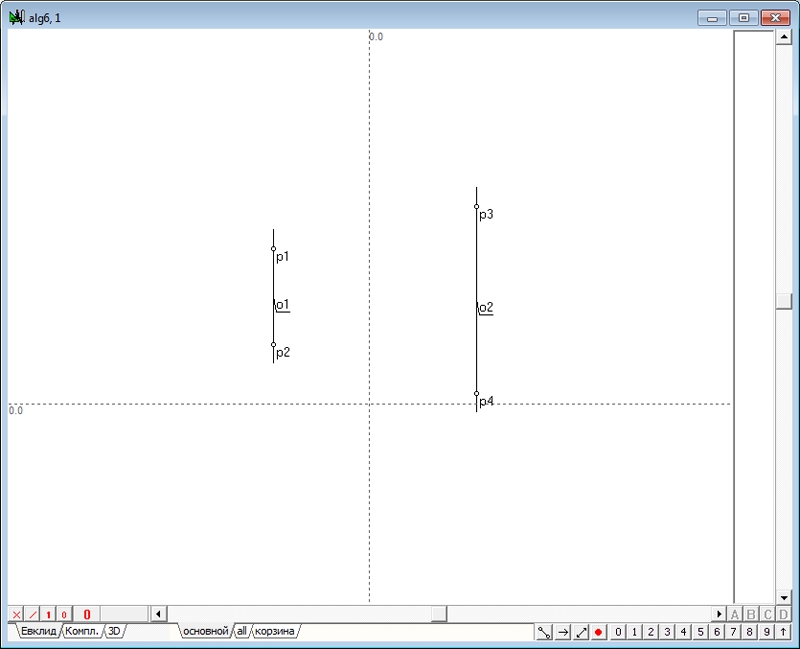
| 60 | Нам потребуется еще один алгоритм, который позволит находить плоскости, перпендикулярные к заданной прямой в ее точке. Создадим еще один пустой алгоритм. Сформируем модели двух пространственных точек.
Рис. 75 |
||
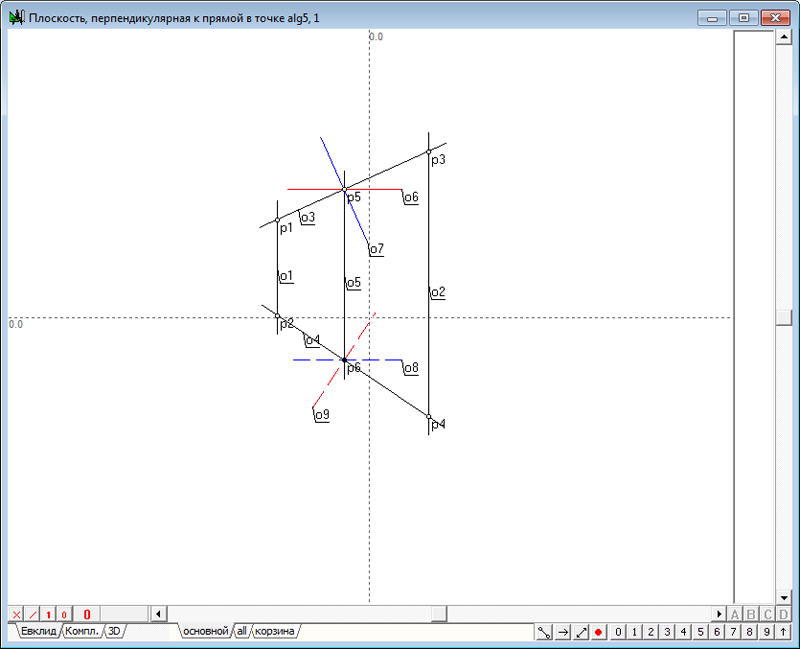
| 61 | Реализуем простое построение в соответствии с принципом построения перпендикулярных плоскостей. Соединим соответственные проекции точек прямыми, удерживая нажатой клавишу Ctrl щелкнем левой кнопкой мыши на прямой o3, чтобы получить точку p5, принадлежащую данной прямой. Выделив точку, и нажав на клавишу с символом v проведем линию связи o5, а затем, добавив к выделению прямую o4 найдем пересечение линии связи и этой прямой с помощью нажатия на клавишу с символом p. Проведем через точку p5 прямую линию, выделив ее и нажав на клавиатуре клавишу с символом h. Выделим точку p6 и прямую o4. Нажатием на клавишу o построим прямую o9, ортогональную к прямой o4. Назначим соответственные атрибуты полученным линиям. Аналогично построим проекции второй прямой перпендикулярной плоскости - прямые o7 и o8. Создадим интерфейс алгоритма. В качестве входных параметров укажем прямые o3 и o4, а также точки p5 и p6. В качестве выходных параметров назначим прямые o6, o9, o7 и o8. Дадим название алгоритму - Плоскость, перпендикулярная к прямой в точке.
Рис. 76 |
||
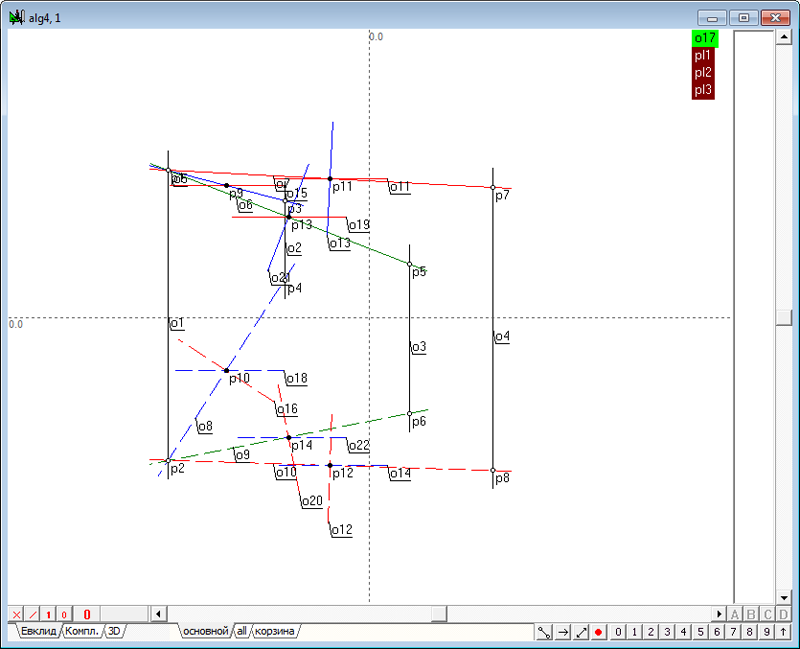
| 62 | Воспользуемся только что созданным алгоритмом для построения трех плоскостей, перпендикулярных трем отрезкам в проектируемом алгоритме alg4. Сформируем группы, включающие в себя данные этих плоскостей.
Рис. 77 |
||
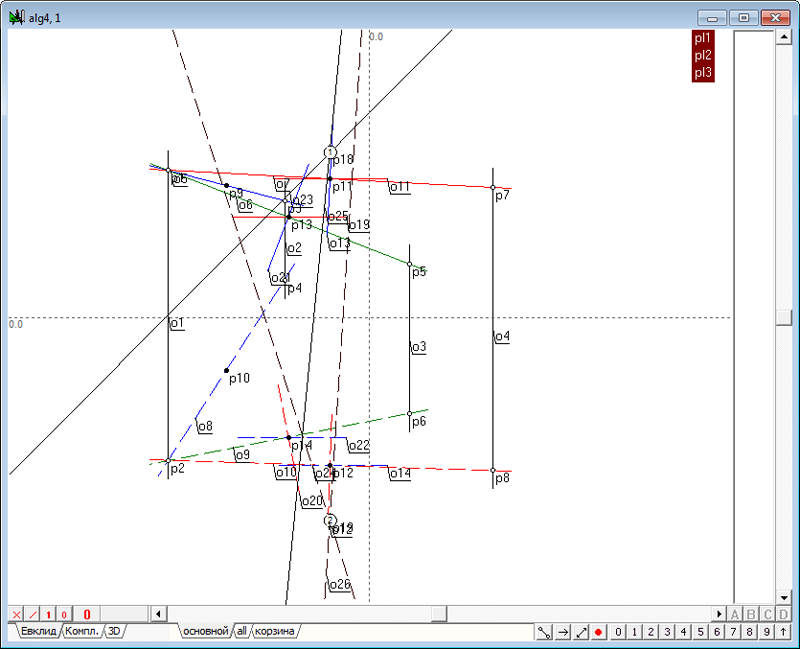
| 63 | Пересечем любые две пары этих плоскостей с получением моделей двух прямых линий, а затеи найдем проекции точек пересечения этих прямых.
Рис. 78 |
||
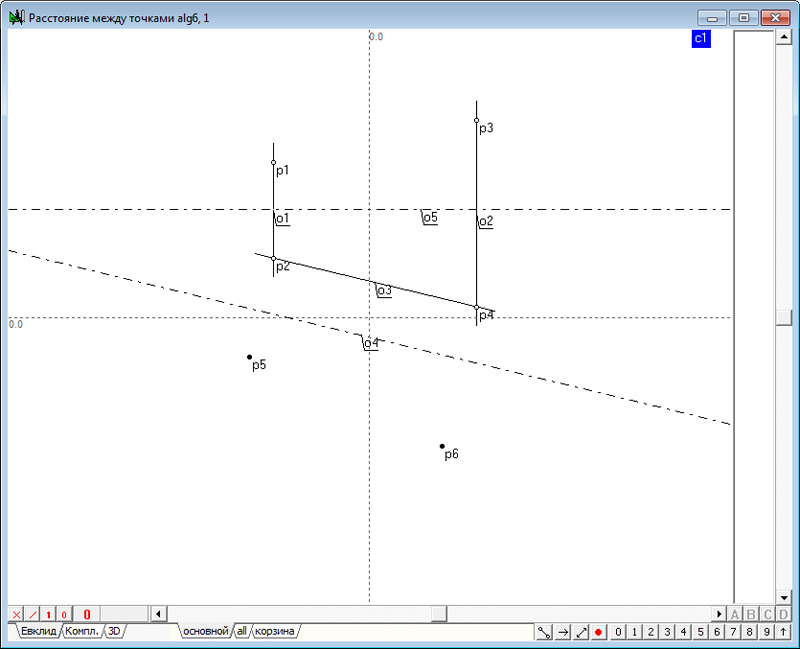
| 64 | Необходимо создать еще один алгоритм, позволяющий определить расстояние между двумя точками, расположенными в пространстве. Создадим новый алгоритм и сформируем модели двух точек.
Рис. 79 |
||
| 65 | Соединим вторые проекции точек и проведем ось для новой системы плоскостей проекций, параллельно второй проекции линии - o3. Найдем проекции исходных точек в третьем поле. Поскольку прямая линия в системе полей проекций 2-3 является линией уровня, то в третьем поле проекция такой прямой изображается в натуральную величину, а следовательно, расстояние между точками p5 и p6 является искомой длиной отрезка, соединяющего две точки, расположенные в пространстве. Назначим входные и выходные параметры алгоритма и дадим ему название - Расстояние между точками.
Рис. 80 |
||
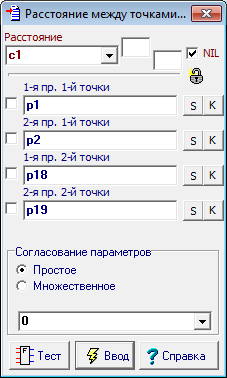
| 66 | Воспользуемся только что созданным алгоритмом для решения задачи о нахождении расстояния от точки пересечения серединных перпендикулярных плоскостей до любой из исходных точек.
Рис. 81 Вычисленное расстояние c1 позволяет образовать первую и вторую проекции очерков сферы, проходящей через четыре заданные точки.
Рис. 82 |
||
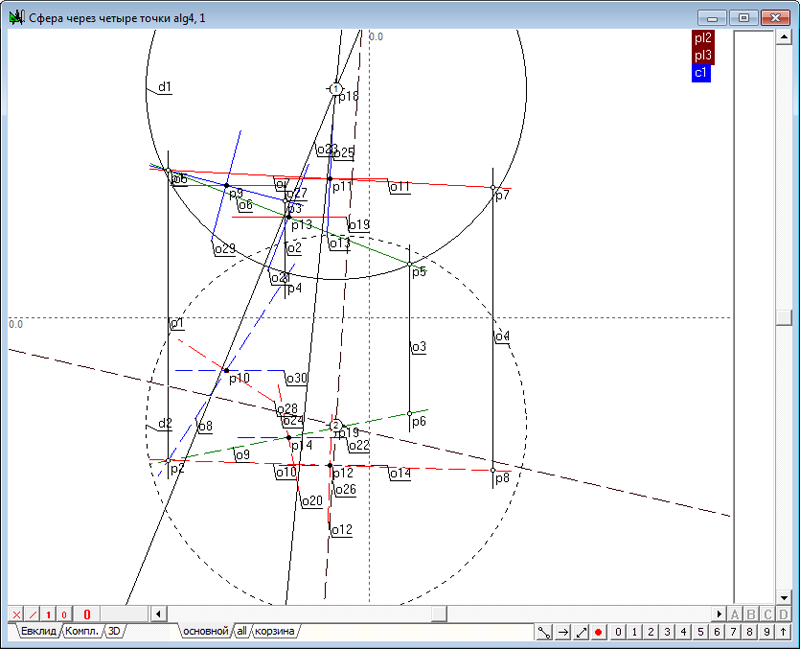
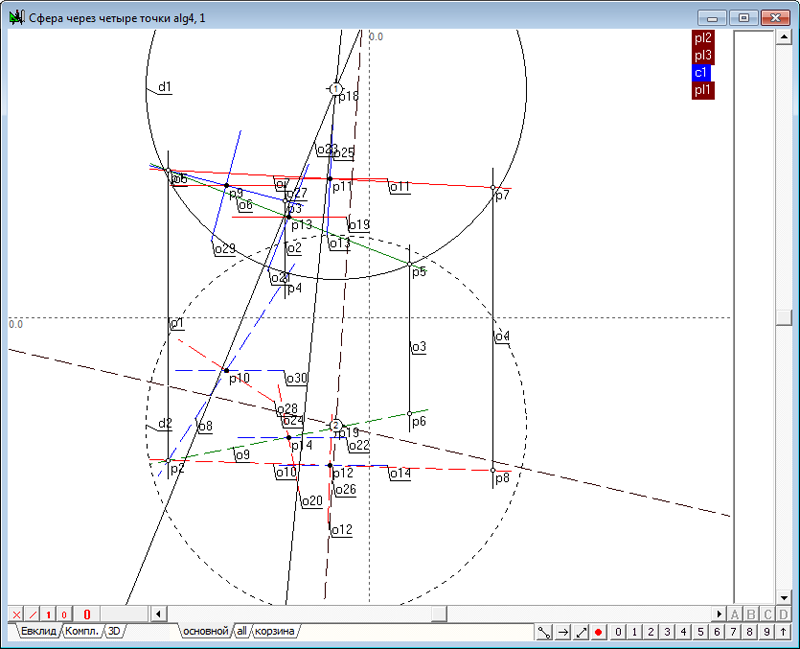
| 67 | В качестве входных параметров алгоритма укажем первые и вторые проекции всех четырех исходных точек. В качестве выходных параметров назначим окружности d1 и d2. Дадим название алгоритму - Сфера через четыре точки.
Рис. 83 |
||
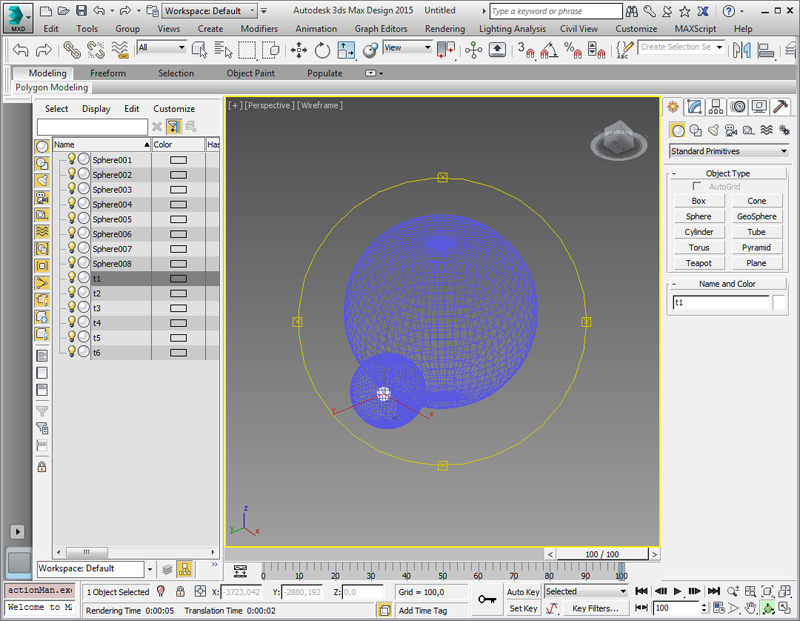
| 68 | Теперь в Главном алгоритме можно построить искомые очерки двух сфер, проходящих касательно по отношению к четырем исходным сферам. Сформируем группы для полученных сфер, назвав их sfr1 и sfr2. Для формирования изображения, иллюстрирующую данную задачу, средствами системы 3DStudio Max, сформируем команды языка Max Script, воспользовавшись функциями синтеза таких команд на основе данных проекта системы Симплекс. Перейдем в закладку Max и выберем функцию Script Sphere. Создадим следующие скрипты: t1 для сферы sph1; Используя команду Файл из закладки Текст, сформируем операцию записи данных на носитель информации, указав в качестве Названия файла текстовую константу, например, "sfr.ms", а в качестве Содержимого перечислим t1,t2,t3,t4,t5. В результате на носителе информации будет создан файл sfr.ms, в котором на языке Max Script будут записаны данные о рассчитанных сферах. Данный скрипт можно загрузить в систему 3DStudio Max командой MAXScript/Run Script..., после чего сцена с моделями и изображениями сфер будет доступна для редактирования и обработки средствами системы 3DStudio Max.
Рис. 84 |
||
| 69 | Так, например, на приведенном рисунке представлен результат рендеринга сцены, составленной из рассчитанных в проекте сфер.
Рис. 85 |
||
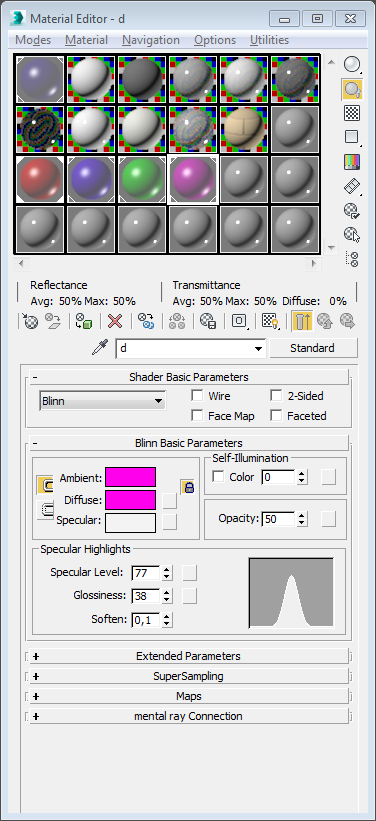
| 70 | Для визуализации сфер необходимо настроить параметры материалов таким образом, чтобы задать их полупрозрачность, в противном случае сферы, участвующие в построении, могут быть не видны. Имеет смысл включить в состав скрипта и точки касания сфер, воспользовавшись для этого командой Script Point и добавив к параметру Содержимого в функции формирования файла sfr.ms соответственные текстовые переменные, содержащие скрипты для описания точек касания t6,t8,t9,t10,t11,t12,t13,t14,t15.
Рис. 86 |
||
| 71 |
Рис. 87 |
||
В приведенных ссылках содержатся файл сцены, реализованной на языке MaxScript и проект соответственного построения, реализованный в системе Симплекс. |