|
||
| 1 | Построим сферу, проходящую через четыре несовпадающие точки, расположенные в трехмерном пространстве. Идея алгоритма состоит в следующем: все точки сферы одинаково удалены от ее центра. Возьмем первую и вторую точки, задающие сферу и найдем то множество точек, которые равноудалены от них. Понятно, что такие точки будут находиться на плоскости, проходящей через центр отрезка, соединяющего первую и вторую точку, причем эта плоскость будет перпендикулярна этому отрезку. Аналогичные рассуждения можно провести в отношении первой и третьей, а также первой и четвертой точек. Таким образом, будет образовано три несовпадающие плоскости, определенные на парах обозначенных выше точек. Как известно, три несовпадающие плоскости пересекаются в единственной точке. Понятно, что эта точка будет удалена на равные расстояния от всех четырех точек, задающих сферу. Она и будет являться центром искомой сферы. Для определения радиуса сферы необходимо измерить длину отрезка между центром сферы и любой из задающей ее точек. Задача сводится к решению следующих подзадач: - нахождение середин отрезков, соединяющих первую точку с остальными точками; Приступим к реализации алгоритма решения задачи.
|
|
Для решения поставленной задачи нам потребуется использовать алгоритм пересечения двух плоскостей. Такой алгоритм уже был разработан в проекте под названием "Пересечение плоскостей". Для того чтобы не создавать его заново, воспользуемся примером из этого проекта, загрузим его в систему Симплекс и скопируем алгоритм пересечения плоскостей в буфер Clipboard. Для этого перейдем в окно алгоритма Прямая пересечения двух плоскостей, вызовем контекстное меню этого окна щелчком правой кнопки мыши и выберем в нем пункт Алгоритм... В появившемся окне следует перейти в Список алгоритмов проекта, выделить в нем алгоритм alg1 и, вызвав контекстное меню, выбрать пункт Копировать "alg1". В результате этого действия алгоритм и описание всех его параметров будут занесены в буфер Clipboard. Впоследствии мы вставим эту информацию в наш новый проект, реализующий задачу построения сферы по четырем точкам. Теперь можно закрыть окно Список алгоритмов и вызвать команду создания нового проекта Ctrl+N. |
||
| Разместим курсор над открывшимся окном алгоритма Главный и, вызвав контекстное меню щелчком правой кнопки мыши, выберем пункт Вставить. В ответ на это действие система задаст вопрос о том, каким образом согласовать имена объектов алгоритма, хранящихся в буфере Clipboard, с именами объектов в алгоритме, в который производится вставка. Потенциально в алгоритмах могут быть объекты с одинаковыми именами, что может привести к конфликту состава отношений алгоритма. Но, поскольку, алгоритм Главный пуст, никаких конфликтов не возникнет и мы сможем произвести обыкновенную вставку, не выполняющую операцию замены имен вставляемого алгоритма на новые, неиспользуемые в алгоритме-приемнике. | ||
Выполненная вставка не приводит к каким-либо видимым изменениям в проекте. Проверить то, что изменения все-же произошли, можно, вызвав из контекстного меню пункт Алгоритм, и убедиться в том, что в состав алгоритма включен алгоритм alg1 (Прямая пересечения двух плоскостей). В настоящий момент имеет смысл выполнить команду сохранения проекта в файле на носителе информации, обратившись к пункту главного меню Файл/Сохранить как... |
||
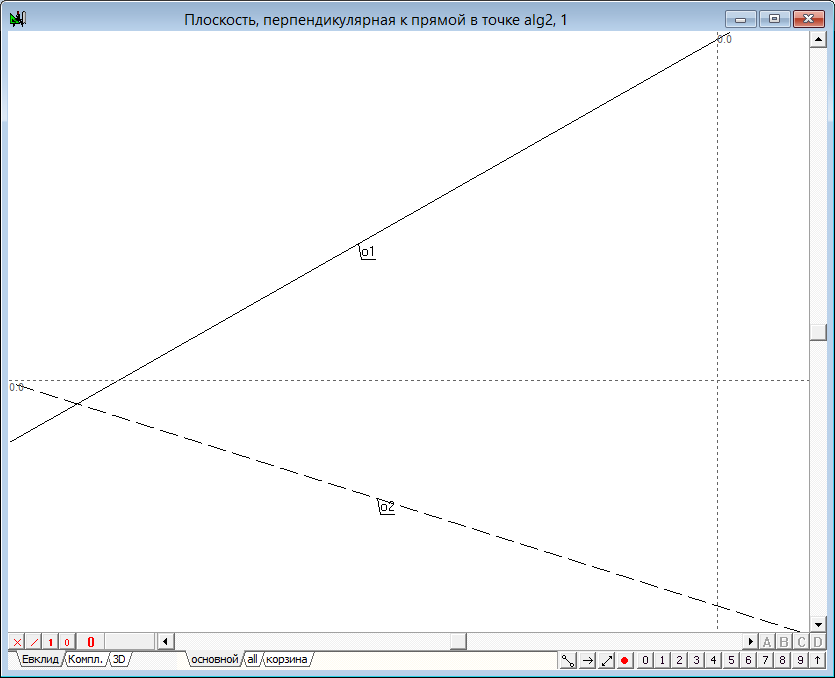
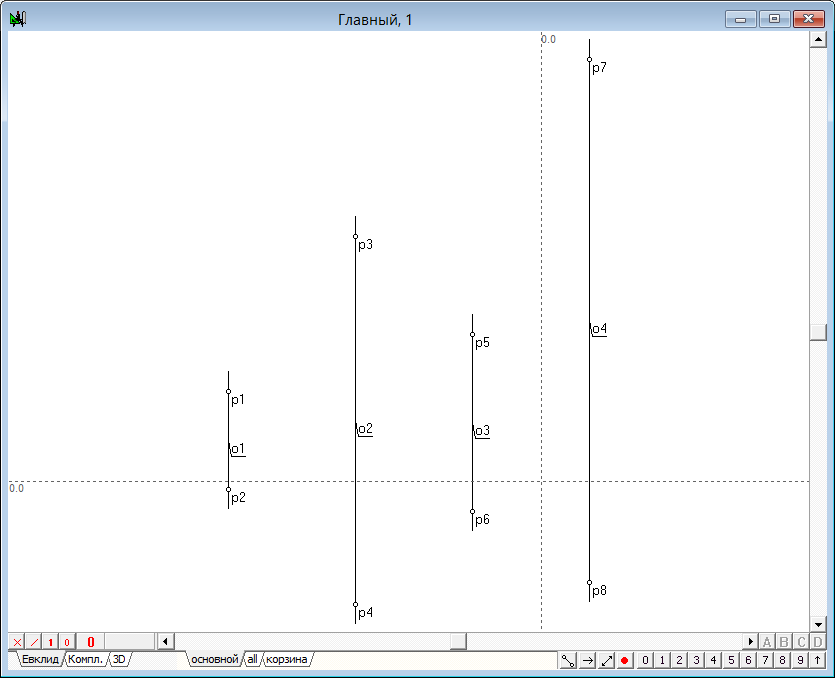
| Для решения задачи потребуется еще один алгоритм, отвечающий за построение плоскости, проходящей через точку и перпендикулярной к заданному отрезку. Пользуясь командой проведения Свободной прямой, построим две произвольные линии o1 и o2, являющиеся проекциями некоторой прямой, расположенной в трехмерном пространстве. Изменим атрибут линии o2 на пунктирное начертание, для того чтобы визуально соотносить эту линию с объектами горизонтального поля проекций | ||
Рис. 1 |
||
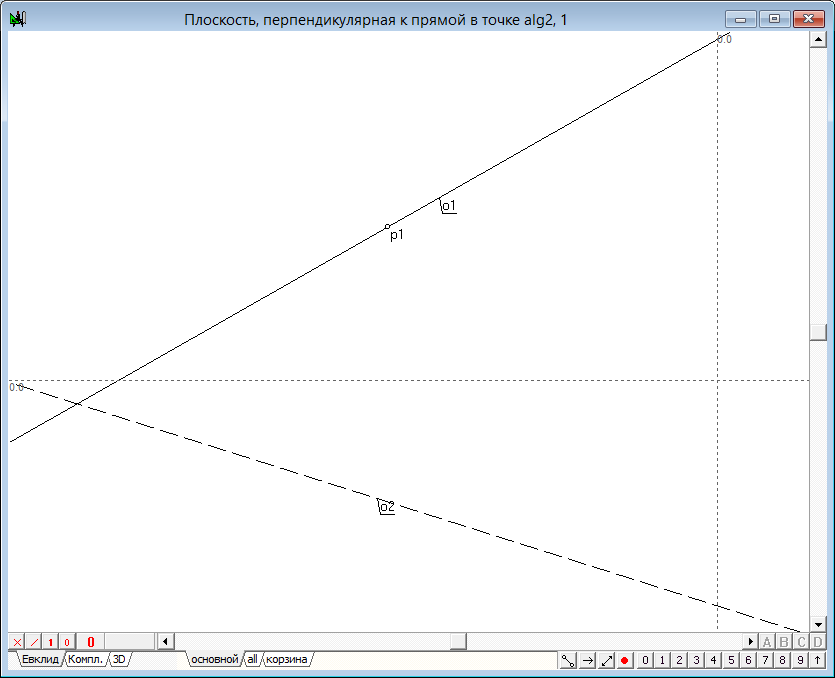
| 2 | Разместим курсор где-нибудь над прямой o1 и выполним щелчок левой кнопкой мыши при нажатой клавише Ctrl, чтобы сгенерировать точку, принадлежащую прямой o1. | |
Рис. 2 |
||
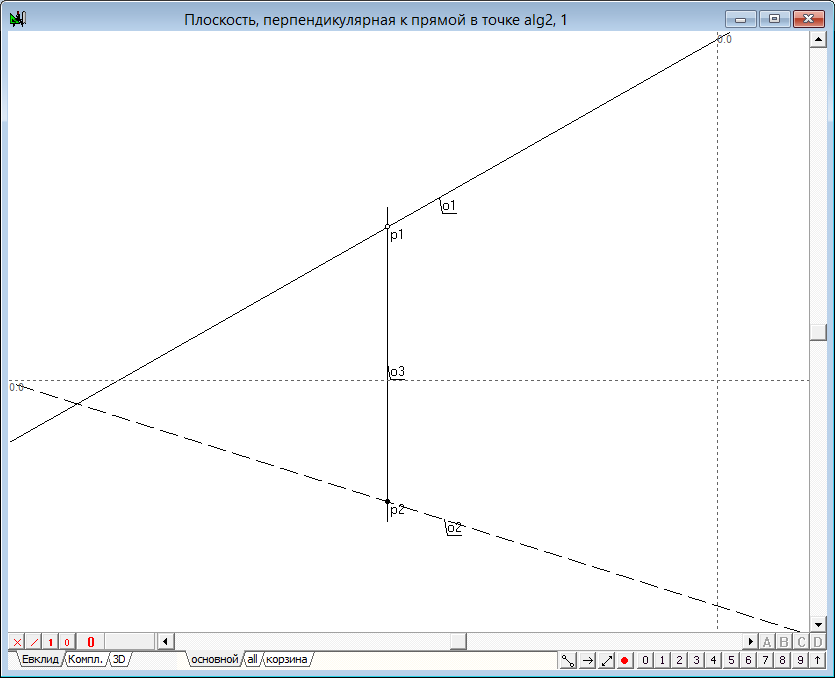
| 3 | Проведем через точку p1 вертикальную линию связи, предварительно выделив эту точку и нажав на клавиатуре кнопку с латинским символом v. Добавим к полученной и выделенной в данный момент линии o3 линию o2, удерживая при этом нажатой клавишу Shift, и нажмем на клавиатуре клавишу с латинским символом p, для того чтобы найти точку p2 пересечения двух прямых линий o2 и o3. | |
Рис. 3 |
||
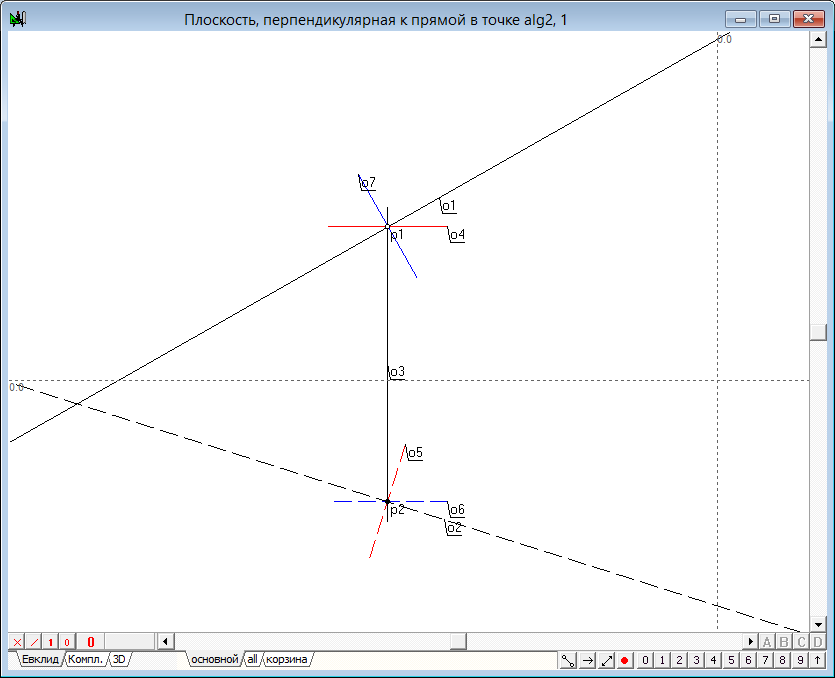
| 4 | Прямые линии, задающие искомую плоскость, строятся следующим образом:
- горизонтальная проекция первой прямой плоскости o5 должна пройти перпендикулярно горизонтальной проекции исходной прямой через точку p2. Для ее построения выделим два объекта - точку p2 и прямую o2 и нажмем на клавиатуре клавишу с латинским символом o. Изменим атрибуты отображения этой прямой. Проекции второй прямой плоскости строятся по аналогичному правилу лишь с той разницей, что теперь проекция прямой на горизонтальную плоскость должна проходить через точку p2 и быть строго горизонтальной, в то время как фронтальная проекция должна быть перпендикулярной фронтальной проекции исходной прямой и проходить через точку p1. |
|
Рис. 4 |
||
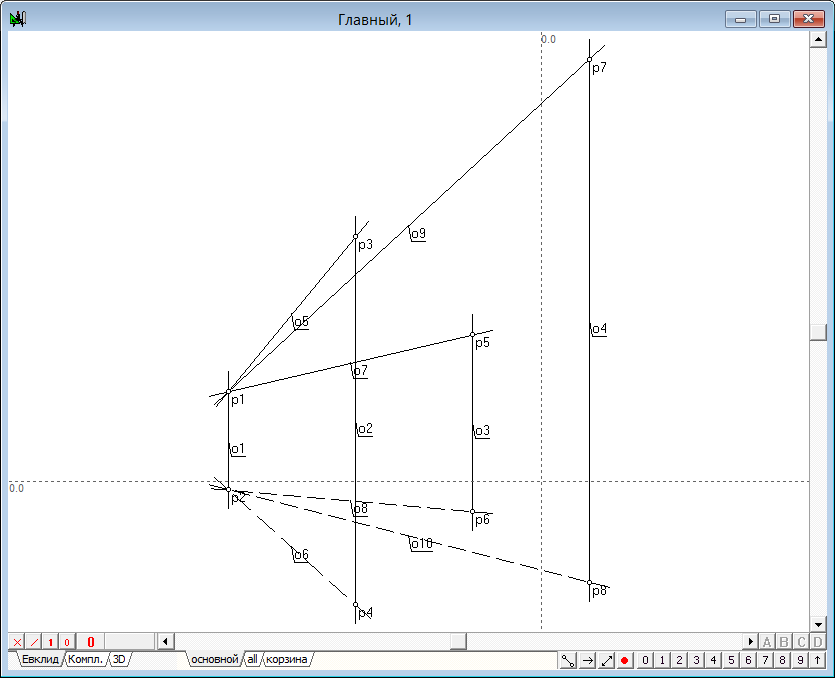
| 5 | Реализация алгоритма выполнена. Теперь необходимо определить интерфейс взаимодействия с алгоритмом. Выделим последовательно объекты o4, o5, o7, o6 и, вызвав контекстное меню, назначим их выходными параметрами алгоритма. Вход алгоритма определим следующим образом: Выделим объекты p1, p2, o1, o2 и назначим их входными параметрами алгоритма. Укажем имя алгоритма (Плоскость, перпендикулярная к прямой в точке) и названия входных и выходных параметров. p1 - 1-я проекция точки; o4 - 1-я проекция 1-ой прямой плоскости; |
|
Приступим к решению основной задачи. Перейдем в окно алгоритма Главный и разместим в поле чертежа модели четырех точек, расположенных в трехмерном пространстве. Для этого, перемещая курсор по полю чертежа, будем нажимать на клавишу с латинским символом V (верхний регистр). Следует обратить внимание на то, что перед вводом каждой очередной команды необходимо снимать выделение, переводя курсос в поле, свободное от изображений объектов чертежа, и щелкая левой кнопкой мыши. |
||
Рис. 5 |
||
| 6 | Соединим первую точку с остальными посредством трех отрезков. Для этого, удерживая клавишу Shift выделим точки p3, p5, p7 и p1. Точка p1 обязательно должна быть выбрана последней. Нажав на клавиатуре датинскую клавишу o, получим три прямые линии o5, o9 и o7, исходящие из точки p1. Аналогичным образом строим линии o6, o8 и o10. | |
Рис. 6 |
||
| 7 | Найдем средние точки отрезков построенных прямых линий. Для этого, удерживая нажатой клавишу Shift, выделям необходимые прямые и нажимаем латинскую клавишу c. | |
Рис. 7 |
||
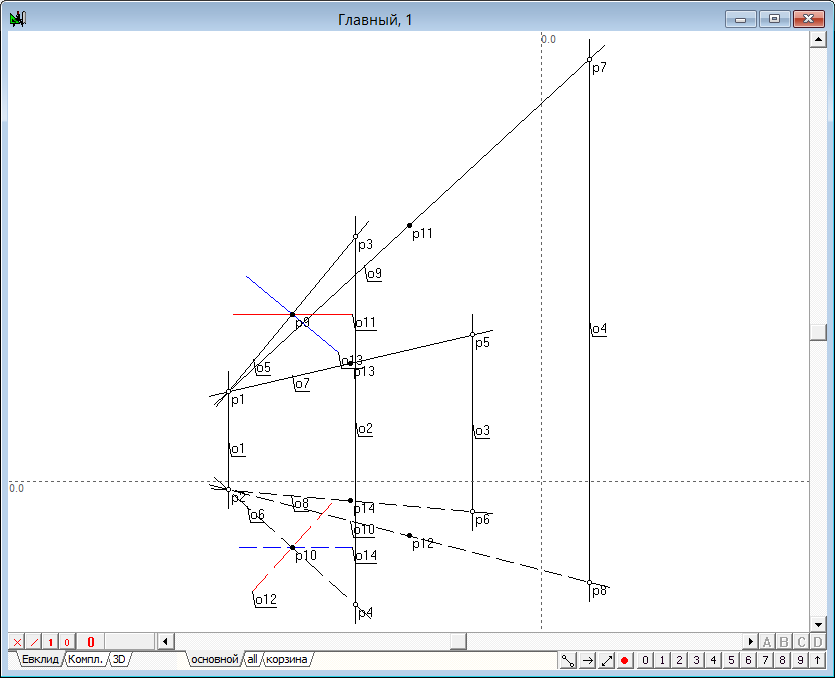
| 8 | Пользуясь созданной ранее функцией Плоскость, перпендикулярная к прямой в точке, зададим три плоскости | |
Рис. 8 |
||
Рис. 9 |
||
Рис. 10 |
||
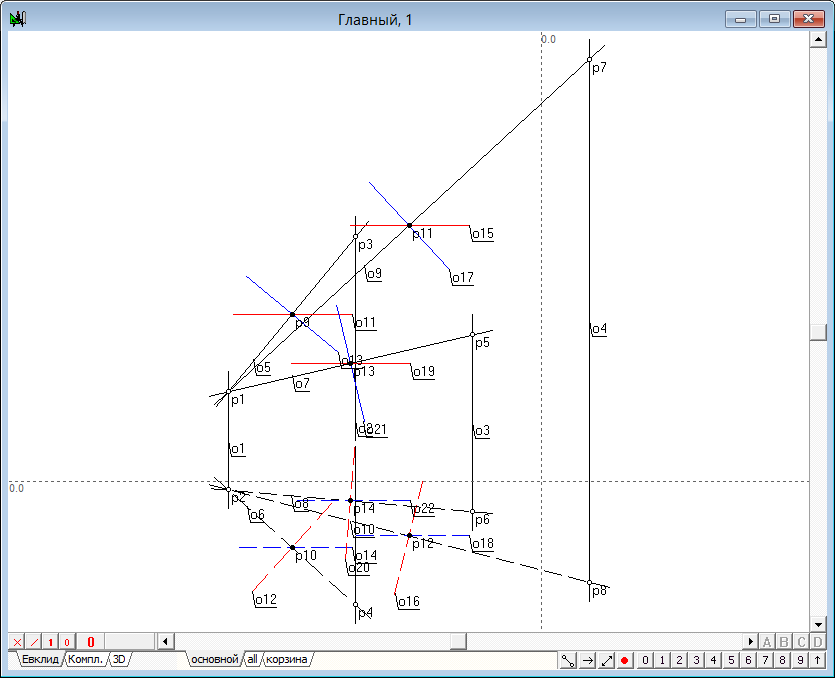
| 9 | Найдем линии пересечения пар построенных плоскостей | |
Рис. 11 |
||
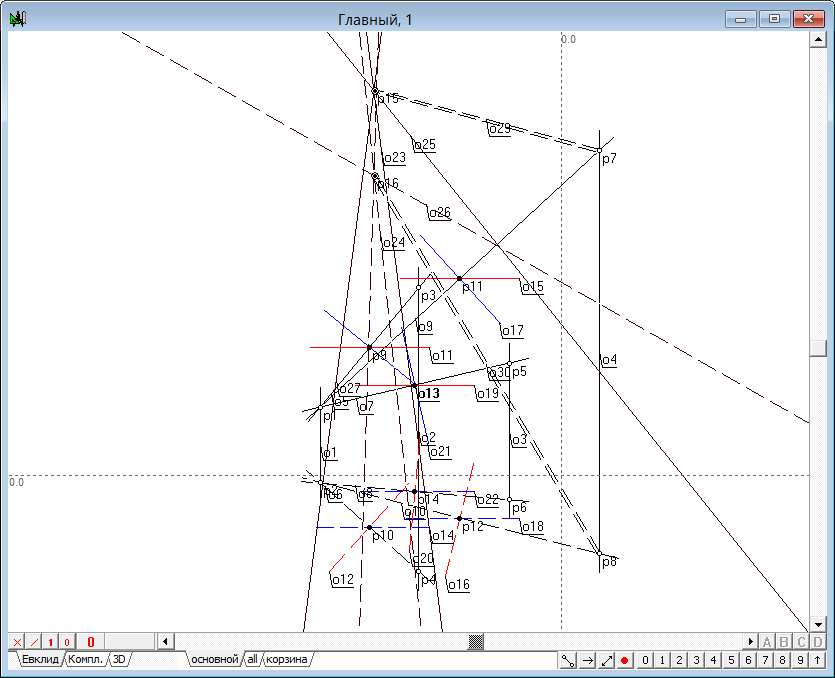
| 10 | Из чертежа видно, что все три прямые проходят через одну и ту же точку в пространстве. Выбрав любые две прямые, найдем эту точку (p15, p16). Эта точка является центром сферы, проходящей через заданные точки. Для нахождения радиуса этой сферы построим отрезок, исходящий из центра сферы на одну из исходных точек. | |
Рис. 12 |
||
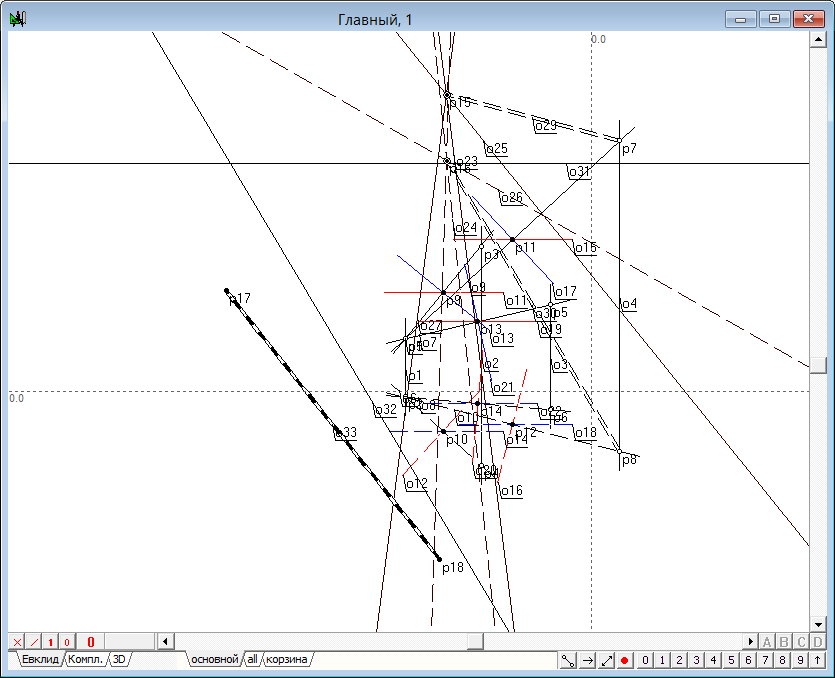
| 11 | Определение истинной величины отрезка осуществляется путем перевода отрезка в третье поле, ось которого в пересечении со вторым полем располагается параллельно горизонтальной проекции отрезка. | |
Рис. 13 |
||
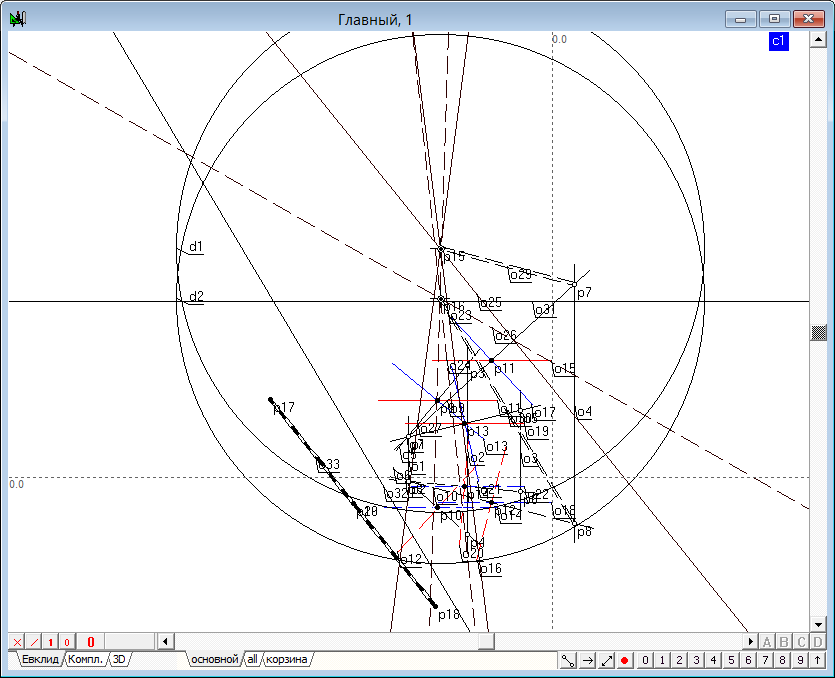
| 12 | Измерив длину отрезка c1, построим модель сферы в виде двух окружностей с радиусом c1. | |
Рис. 14 |
||
| 13 | Поставленная задача решена. Для проверки корректности решения покажем, что одна из исходных точек действительно лежит на сфере. Для этого выберем точку, например (p5-p6) и через ее фронтальную проекцию проведем проецирующую плоскость (o34), параллельную горизонтальной плоскости проекций. Эта плоскость будет изображена прямой линией o34. Плоскость рассекает сферу по окружности. На виде сверху эту окружность легко построить, взяв в качестве центра точку p16. Радиус окружности определяется точкой p23, являющейся проекцией точки p22 пересечения линии o34 с очерком сферы - окружностью d1 на прямую o35. Как следует из чертежа, окружность d3, изображающая горизонтальную проекцию сечения сферы плоскостью, проходит через вторую проекцию тестируемой точки - точку p6, что и следовало показать. Таким образом, исходная точка, заданная проекциями p5-p6 действительно лежит на поверхности сферы. | |
Рис. 15 |
||