ЕДИНЫЙ КОНСТРУКТИВНЫЙ АЛГОРИТМ ПОСТРОЕНИЯ ФОКУСОВ КРИВЫХ ВТОРОГО ПОРЯДКА
Д.В.ВОЛОШИНОВ
Санкт-Петербургский государственный университет телекоммуникаций им. проф.М.А.Бонч-Бруевича (Санкт-Петербург)
denis.voloshinov@yandex.ru

A UNIFIED CONSTRUCTIVE ALGORITHM FOR FOCI OF CURVES OF THE SECOND ORDER PRODUCTION

Аннотация

При использовании обычных инструментальных средств для решения геометрических задач, получение и анализ результатов, в которых фигурируют мнимые геометрические образы, затруднительны. Несмотря на признание правомерности и научной ценности мнимых решений, присутствующих в геометрических конструкциях, до сих пор не вполне ясным остается вопрос о целесообразности и практической исполнимости таких решений. В следствие этого, для большинства специалистов-практиков мнимые решения представляются как нечто недостижимое или неважное. Однако внедрение мнимостей в практику геометрического моделирования позволяет получать решения в исчерпывающей полноте, разрабатывать единые алгоритмы решения задач, которые обычно представлялись либо не решаемыми, либо сводились к решениям в частных постановках. Использование компьютерных технологий и парадигмы конструктивного геометрического моделирования позволяют снять остроту этой проблемы и направить усилия как на совершенствования геометрической теории, так и на внедрение научных достижений в обозначенной области в область практических применений. Средства автоматизации геометрического эксперимента позволяют найти в, казалось бы, в давно известных математических фактах новые закономерности, прийти к более общему пониманию геометрических понятий и образов.

Статья посвящена анализу некоторых геометрических схем и обсуждению возникающих в этой связи вопросов теории построения кривых второго порядка методами конструктивного синтеза. В статье показано, что используемые в настоящее время определения центра кривой второго порядка и диаметров этих кривых вступают в противоречие с принципом неразличимости коник в проективной геометрии. Предложены пути устранения этих противоречий и на их основе разработан унифицированный алгоритм построения фокусов кривых второго порядка.

Abstracts

While using conventional tools for solving geometric problems, it is difficult to obtain and analyze results when imaginary geometric images appear. Despite the recognition of the legitimacy and scientific significance of imaginary solutions presented in geometric constructions, the task of the feasibility and practical receiving of such solutions remains unclear. That’s why, for most practitioners imaginary solutions are presented as unattainable or unimportant. However, the introduction of imaginary images into the practice of geometric modeling makes it possible to obtain solutions in an exhaustive manner, to develop unified algorithms for solving problems that were usually either not solvable or reduced to solutions in partial productions. The use of computer technologies and the paradigm of constructive geometric modeling make it possible to eliminate the acuteness of this problem and direct efforts both to improve the geometric theory and to introduce scientific achievements in this area to the field of practical applications. The means of automating a geometric experiment make it possible to find new regularities in seemingly well-known mathematical facts, to come to general understanding of geometric concepts and images.

The article is devoted to the analysis of some geometric schemes and to the discussion of some problems of the theory of curves of the second order constructing by the methods of geometrical synthesis. The article shows that the currently used definitions of the center of the second-order curve and the diameters of these curves contradict the principle of the indistinguishability of conics in projective geometry. The ways of eliminating these contradictions are proposed and on their basis a unified algorithm for constructing the foci of the second order curves is developed.

Ключевые слова: геометрическое моделирование; кривая второго порядка; коника; фокус; Симплекс.

Keywords: geometric modeling; curve of second-order; conic; foci; Simplex.

Принципы определения фокальных точек кривых второго порядка освещены в научной и педагогической литературе столь широко и подробно, что попытка отыскать в этом вопросе что-то новое и значимое может вызвать у читающего эти строки глубокое удивление и недоумение [1–3, 5, 12, 13, 15–20, 21–30]. И все же статья, представляемая на суд читателей, призывает обратить внимание на, казалось бы, хорошо известные факты и устоявшиеся представления с несколько иной точки зрения, нежели это принято делать в математической литературе. Рассуждения предполагается проводить без использования аналитического аппарата математики с опорой на конструктивно-геометрические свойства исследуемых образов и их свойств. Эти рассуждения, основывающиеся на аппарате проективной геометрии, позволят вскрыть ряд противоречий в ныне существующих определениях, относящихся к кривым второго порядка, а их устранение предоставит возможность разработать единый подход к построению некоторых геометрических образов, инициируемых кривыми второго порядка, и дать им общее конструктивное обоснование. Как известно, аффинная геометрия, не оперирующая понятием бесконечности, различает несколько видов кривых второго порядка, среди которых в дальнейшем нас будут интересовать, в особенности, эллипс и гипербола. С точки зрения проективной геометрии кривые второго порядка не различаются, вследствие чего алгоритмы получения тех или иных образов, ассоциированных с понятием конического сечения, также не различаются. Тем более удивительным становится тот факт, что вопросы геометрического обоснования таких образов как фокальные точки коник, в проективной геометрии остались без должного внимания, а известные схемы построения этих точек трактуются исходя из метрических соображений и разнятся для эллипсов и гипербол. Такое положение дел нельзя называть удовлетворительным, в особенности, если неполные, а иногда и противоречивые теоретические положения закладываются в основу средств автоматизации процедур геометрического моделирования, поскольку на практике это приводит к нарушению системности и стабильности работы этих средств. Именно такое положение сложилось с интерпретацией кривых второго порядка при разработке системы Симплекс [10], предназначенной для синтеза конструктивных геометрических моделей не только с привлечением аппарата проективной геометрии, но и оперирующей с мнимыми образами, которые неизбежно в этой геометрии возникают. Многочисленные эксперименты и анализ получаемых геометрических схем, проведенные с помощью этой системы [7–9], позволили сделать вывод о том, что некоторые определения, связанные с трактовкой кривых второго порядка, положенные в основу геометрической теории, некорректны. В частности, неверно трактуется понятие центра кривой второго порядка и отсутствие у эллипса второго главного диаметра. Переосмысление этого геометрического феномена и принятие за основу определений в новой трактовке позволяют выработать единый подход к решению задач с участием кривых второго порядка и унифицировать связанные с этими задачами функции системы геометрического моделирования. Обычно под центром кривой второго порядка понимают полюс, в индуцируемом этой кривой полярном преобразовании бесконечно удаленной прямой, принимаемой за поляру [20]. Это определение в равной степени применяется для отыскания центров невырожденных кривых второго порядка: как эллипсов и окружностей, так и гипербол в аффинной трактовке. Как известно, любое коллинеарное преобразование, определенное в плоскости, переводит точку в точку, прямую линию в прямую линию и конику в конику. При этом свойство инцидентности объектов-оригиналов и их образов сохраняется, а метрические свойства объектов, в общем случае, нет. В соответствии с используемым определением центра кривой второго порядка, опять же в общем случае, в коллинеарном преобразовании центр кривой-оригинала не переходит в центр кривой-образа. Поставим перед собой задачу в обратной постановке: допустим, на плоскости имеются две коники $a$ и $b$ . Требуется подобрать такую коллинеацию $\chi$ , которая не только бы переводила конику $a$ в конику $b$ , но и устанавливала бы соответствие между главными диаметрами этих коник. Рассмотрим вначале эту задачу, исходя из предположения, что обе коники – эллипсы. Поскольку эллипсы имею два главных диаметра, то не составит никакого труда найти точки пересечения соответственных диаметров с эллипсами: $P_1$ , $Q_1$ , $R_1$ и $S_1$ для первого эллипса и $P_2$ , $Q_2$ , $R_2$ и $S_2$ . Коллинеарное преобразование $$\chi |\begin{array}{c}{P}_1,Q_1,R_1,S_1\\ P_2,Q_2,R_2,S_2\end{array}$$ обеспечивает не только перевод коники $a$ в конику $b$ , но и соответствие в коллинеации $\chi$ точек $O_1=P_1{Q}_1\times R_1{S}_1$ и $O_2=P_2{Q}_2\times R_2{S}_2$ , т.е. $Q_1=\chi \left(Q_2\right)$ . Такое преобразование частного вида переводит центр одного эллипса в центр другого (рис. 1).

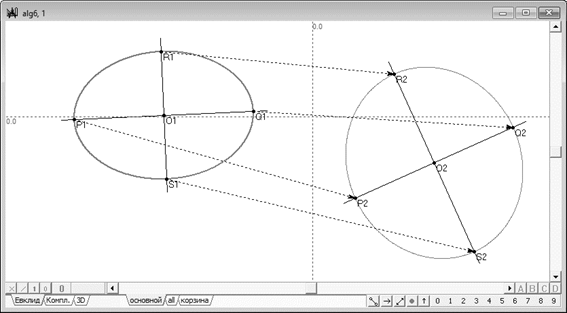
Рис. 1. Коллинеарное преобразование, переводящее эллипс в другой эллипс с сохранением соответствия главных диаметров эллипсов

Теперь выполним аналогичную процедуру, но с той лишь разницей, что соответствие будем устанавливать между гиперболой $a$ и эллипсом $b$ . На этом этапе возникает первая сложность: общеизвестно, что гипербола имеет только один действительный главный диаметр. Второй дополнительный диаметр, обычно называемый «мнимым», несмотря на то, что он проходит через центр и представлен действительной прямой, пересекает гиперболу в двух мнимых комплексно-сопряженных точках и попытка установить коллинеацию, подобную той, что была рассмотрена выше, конику $a$ в конику $b$ не переведет. Однако отсутствие второго действительного диаметра у гиперболы легко восполнить, отказавшись от аффинных представлений о решаемой задачи и перейдя к понятиям проективной геометрии. Сделаем предположение о том, что вторым диаметром гиперболы является бесконечно удаленная прямая и проверим, не противоречит ли данное предположение каким-либо другим свойствам кривых второго порядка. Первое, что следует отметить, что этот диаметр является действительным, а не «мнимым», который по обыкновению приписывают гиперболе. Второе и исключительно важное для решения поставленной задачи свойство: коника дважды пересекает бесконечно удаленную прямую в различных бесконечно удаленных точках, что и должно иметь место на диаметре коники. Таким образом, сделав это предположение, получаем четыре точки на конике: две собственные $P_1$ , $Q_1$ от единственного собственного диаметра гиперболы и две несобственные точки плоскости $R_1^{\infty }$ , $S_1^{\infty }$ от несобственного диаметра коники. Установим коллинеацию $\chi |\begin{array}{c}{P}_1,Q_1,R_1^{\infty },S_1^{\infty }\\ P_2,Q_2,R_2,S_2\end{array}$ . В этой коллинеации гипербола $a$ полностью перейдет в эллипс $b$ , причем $P_2{Q}_2=\chi \left(P_1{Q}_1\right)$ и $R_2{S}_2=\chi \left(R_1^{\infty }{S}_1^{\infty }\right)$ . Следует обратить внимание на то, что в данной коллинеации точке $O_2=P_2{Q}_2\times R_2{S}_2$ соответствует несобственная точка $O_1^{\infty }=P_1{Q}_1\times R_1^{\infty }{S}_1^{\infty }$ , то есть центру эллипса $b$ не-центр гиперболы $a$ (рис. 2). Кажущееся противоречие, однако, оказывается вполне конструктивным.

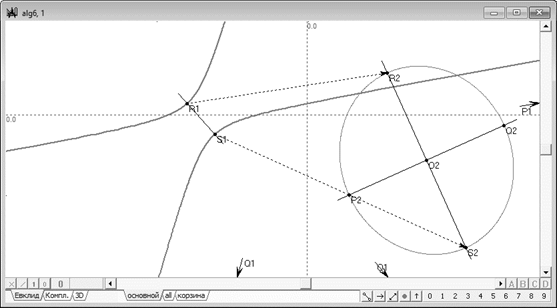
Рис. 2. Коллинеарное преобразование, переводящее эллипс в другой эллипс с сохранением соответствия главных диаметров эллипсов

Определим обратную коллинеацию ${\chi }^{-1}|\begin{array}{c}{P}_2,Q_2,R_2,S_2\\ P_1,Q_1,R_1^{\infty },S_1^{\infty }\end{array}$ и проведем через точку $O_2$ множество диаметров $\left\{d_2\right\}$ кривой $b$ . Выполнив преобразование $\left\{d_1\right\}={\chi }^{-1}\left(\left\{d_2\right\}\right)$ , получим множество прямых, параллельных собственному диаметру гиперболы $a$ , в силу своей параллельности пересекающиеся в единственной точке $O_1^{\infty }$ со вторым несобственным диаметром этой кривой (рис. 3). Если же рассмотреть результат пересечения объектов этого множества с «мнимым» диаметром гиперболы, то несложно убедиться в том, что этот результат является бесконечным множеством точек на прямой линии, пересекающейся с коникой $a$ в мнимых точках. В данном контексте говорить о мнимом диаметре, как об объекте, проявляющем какие-либо свойства диаметра кривой, не приходится. Зато вполне уместно считать, что все различные линии множества $\left\{d_1\right\}$ пересекаются в единственной точке $O_1^{\infty }$ , в которой, в том числе, с этими диаметрами пересекается несобственный главный диаметр гиперболы. По этой и по ряду других причин, которые будут приведены ниже, центром гиперболы рационально считать именно эту точку $O_1^{\infty }$ и отказаться от определения, констатирующего, что центром кривой второго порядка является результат полярного преобразования бесконечно удаленной прямой в отношении этой коники [4, 6, 11, 14, 20].

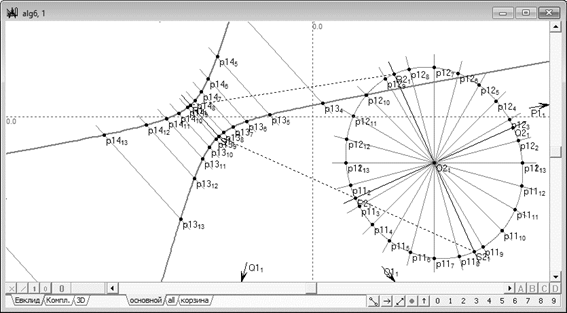
Рис. 3. Соответствие диаметров эллипса и диаметров гиперболы в преобразовании коллинеации

Проведем через точки пересечения главных диаметров эллипса с самим эллипсом касательные прямые и найдем результат их преобразования в коллинеации ${\chi }^{-1}$ . В результате получим четыре прямые линии, две из которых будут касательными к конике $a$ в точках $P_1$ и $Q_1$ , а две остальные станут асимптотами, приближающимися к гиперболе и соединяющимися с ней в бесконечно удаленных точках $R_1^{\infty },$ и $S_1^{\infty }$ . В этом контексте последние две прямые допустимо считать касательными к коникам и не делать различия между ними и касательными прямыми в обычном понимании (рис. 4).

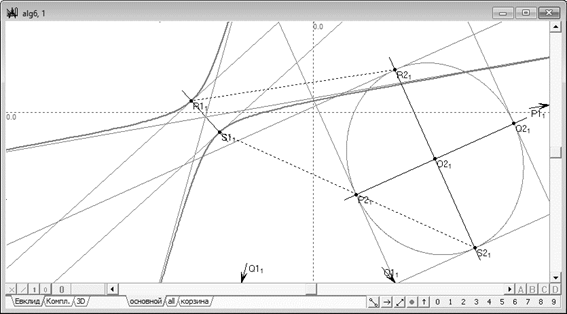
Рис. 4. Соответствие касательных в точках пересечения коник с главными диаметрами в преобразовании коллинеации

Выполненное преобразование позволяет обнаружить общность в схемах построения фокальных точек эллипса и гиперболы и свести их в единый алгоритм. Рассмотрим вначале процедуру построения фокальных точек эллипса (рис. 5). Пусть на плоскости задан эллипс $b$ и найдены точки $P,Q,R,S$ пересечения его главных диаметров $f$ и $g$ с ним самим. Построим точку $T$ как результат пересечения касательных $m:m\perp f,m~P$ и $n:n\perp g,n~R$ . Проведем с центром в точке $P$ и через точку $T$ окружность $u$ . Данная окружность пересечет главный диаметр $g$ в точках $F$ и $F^{\prime }$ , которые являются фокальными точками кривой $b$ на оси $g$ .

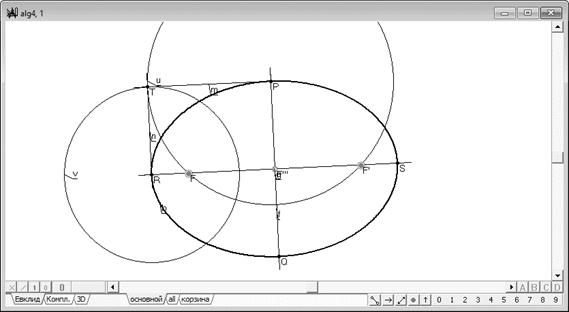
Рис. 5. Построение фокальных точек эллипса

Действуя аналогично, построим окружность $v$ , проходящую через точку $T$ с центром в точке $R$ . Находя пересечение окружности $v$ с диаметром $f$ найдем еще два фокуса $F^{″}$ и $F^{‴}$ коники $b$ , но уже на оси $f$ . Таким образом, мы получили две пары фокальных точек эллипса, каждая из которых может быть образована либо действительными, либо мнимыми точками, причем обе пары не могут быть единовременно действительными или мнимыми. Проведем через точки $F$ и $F^{\prime }$ , взятые как диаметральные, окружность $j$ . Нетрудно заметить, что эта окружность ортогональна к окружностям $u$ и $v$ , а также главным осям $f$ и $g$ коники $b$ . Сказанное будет справедливо и в отношении окружности $i$ , проведенную через точки $F^{″}$ и $F^{‴}$ , взятые как диаметральные. Если одна из окружностей $i$ или $j$ вещественная, то другая обязательно мнимая и наоборот, при этом обе окружности оказываются концентричными, а их центр – вещественная точка. Обратимся теперь к способу построения фокусов гиперболы. В отношении метода построения фокальных точек этой кривой действует схема, схожая со схемой построения фокусов эллипса, однако она некоторые отличия, которые в результате анализа этих схем нам предстоит устранить. Как и в случае эллипса, необходимо найти фокальные точки на обоих главных диаметрах гиперболы посредством построения окружностей. Но, поскольку один из диаметров гиперболы является бесконечно удаленной прямой, то точки пересечения какой бы то ни было наперед заданной окружности с этой прямой являются фиксированными циклическим точками плоскости, поэтому задача выполнения их построения не имеет особого смысла. Следует также заметить, что циклические точки плоскости – мнимые. Поэтому будем строить фокальные точки только на собственном диаметре коники $a$ . Выполним построение точки $T$ как результат пересечения касательных $m:m\perp f,m~P$ и прямой $n$ , касательной к конике $a$ в несобственной точке $S^{\infty }$ . Выберем центр $Z$ окружности $u$ , проведем ее через точку $T$ . Фокальные точки $F$ и $F^{\prime }$ определяются, как точки пересечения окружности $u$ с прямой линией $f$ (рис. 6).

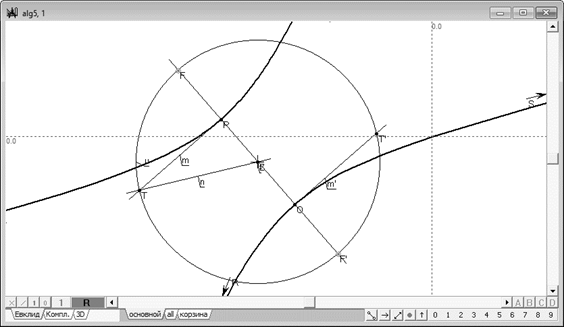
Рис. 6. Построение фокальных точек гиперболы

Из выполненных построений следует, что, в целом, алгоритмы построения фокальных точек эллипса и гиперболы одинаковы. Кажущееся внешнее различие заключается лишь в способе выбора положения центра $Z$ окружности $u$ .

На самом деле, положение точки $Z$ в рассмотренном алгоритме не является определяющим. Обратим внимание на способ построения окружности $u$ как таковой. Несложно заметить, что эта окружность строится на диаметральных точках, которые образуются от пересечения сопряженных пар касательных, проведенных к конике в точках пересечения главных диаметров кривой. Этот геометрический феномен одинаков как в случае решения задачи для гиперболы, так и для эллипса. Вследствие этого, положение точки $Z$ является производным, несмотря на визуальное совпадение положение центра окружности $u$ с характерными точками геометрического построения. Для унификации алгоритмов унифицированный выбор положения точки $Z$ можно трактовать следующим образом: точка $Z$ должна находиться на касательной $n$ , исходящей из точки пересечения главного диаметра с самой кривой, сопряженного с тем, на котором в данный момент осуществляется поиск фокусов. При этом точку $T$ , через которую проходит окружность, следует рассматривать, как диаметральную. Вторая диаметральная точка $T^{\prime }$ определяется пересечением касательной $n$ со второй касательной $m^{\prime }$ , двойственной $m$ . В результате осуществления такого выбора точка $Z$ будет занимать необходимое для решения задачи положение точек $P$ и $R$ при построении фокальных точек эллипса. В результате проведенного анализа приведенных в статье геометрических схем уточнен ряд понятий проективной геометрии, что позволило унифицировать решение задач, связанных с построением фокальных точек кривых второго порядка. Представлен унифицированный алгоритм построения всех четырех фокусов кривой второго порядка. Тем самым заложена основа для расширения областей применения геометрических моделей на мнимые геометрических образы, охватываемые понятием «кривая второго порядка», и проведения исследований, образующихся в этой связи геометрических образов и схем.

Литература

1. Адамар Ж. Элементарная геометрия. Часть I. Планиметрия. M.: Учпедгиз, 1948.— 608 с.
2. Акопян А. В., Заславский А. А. Геометрические свойства кривых второго порядка. М.: МЦНМО, 2007.— 136 с.
3. Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. М.: Учпедгиз, 1957.— 268 с.
4. Белоцерковский Д. Л. Кривые второго порядка на плоскости: методическое пособие. М.: РГУ нефти и газа имени И. М. Губкина, 2009.— 42 с.
5. Берже М. Геометрия: Пер. с франц. М.: Мир.— Т. 2.— 368 с.
6. Васин С. И., Иванов В. И. Аналитическая геометрия. Учебно-методическое пособие для студентов. М.: РГУ нефти и газа имени И.М. Губкина. 2010.— 60 с.
7. Волошинов Д. В. Геометрическая лаборатория. Закладываем основы / Качество графической подготовки: проблемы, традиции и инновации: Материалы VII Международной Интернет-конференции КГП-2017. URL: http://dgng.pstu.ru/conf2017/papers/53/
8. Волошинов Д. В. Геометрическая лаборатория. Инструменты ортогональности / Качество графической подготовки: проблемы, традиции и инновации: Материалы VII Международной Интернет-конференции КГП-2017. URL: http://dgng.pstu.ru/conf2017/papers/72/
9. Волошинов Д. В. Геометрическая лаборатория. Новый геометрический инструмент / Качество графической подготовки: проблемы, традиции и инновации: Материалы VII Международной Интернет-конференциии КГП-2017. URL: http://dgng.pstu.ru/conf2017/papers/60/
10. Волошинов Д. В. Конструктивное геометрическое моделирование. Теория, практика, автоматизация / Д.В.Волошинов. – Saarbrücken: Lambert Academic Publ., 2010. – 355 c.
11. Вольберг А. О. Основные идеи проективной геометрии. М.-Л.: Учпедгиз, 1949.— 188 c.
12. Гирш А. Г. Наглядная мнимая геометрия / А. Г. Гирш. М.: Маска, 2008.— 216 с.
13. Гирш А. Г. Фокусы алгебраических кривых / А.Г. Гирш // Геометрия и графика, 2015.— Т. 3 — С. 4–17. DOI: 10.12737/14415.
14. Глаголев Н. А. Проективная геометрия. М.: Высшая школа, 1963.— 342 с.
15. Дорфман А. Г. Оптика конических сечений. М.: Физматгиз, 1959.— 32 с.
16. Игнатьев Ю. Г., Агафонов А. А. Аналитическая геометрия евклидового пространства. Учебное пособие. I-II семестры. Казань: Изд-во Казанского ун-та, – 2014. – 204 с.
17. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. – 4-е издание. М: Наука, 1978.— С. 64.
18. Короткий В. А., Хмарова Л. И. Начертательная геометрия на экране компьютера / В. А. Короткий, Л. И. Хмарова // Геометрия и графика, 2013.— Т. 1.— С. 32–34.
19. Савельев Ю. А. Графика мнимых чисел // Геометрия и графика, 2013.—Т. 1, № 1.— С. 22–23. DOI: 10.12737/2079.
20. Четверухин Н. Ф. Проективная геометрия. М.: Просвещение, 1953.— 360 с.
21. Audin M. Geometry. Strasbourg, 2002. 363 p.
22. Busemann H., Paul J. Kelly. Projective geometry and projective metrics. New York, Academic press Inc. Publ., 1962. P. 88.
23. Field P. Projective geometry with applications to engineering. New York, D.Van Nostrand Company, 1923. P. 79.
24. Gallier J. Curves and Surfaces In Geometric Modeling: Theory And Algorithms. Philadelphia, University of Pennsylvania, 2015. 492 p.
25. Herman I. The Use of Projective Geometry in Computer Graphics. Berlin, Springer-Verlag, 1992. 148 p.
26. Boissonnat J-D.,Teillaud M. Effective Computational Geometry for Curves and Surfaces With 120 Figures and 1 Table. Springer, 2006. 351 p.
27. Richter-Gebert J. Perspectives on Projective Geometry. A Guided Tour Through Real and Complex Geometry. Berlin, Springer, 2011. 593 p.
28. Lehmer D. N. An Elementary Course In Synthetic Projective Geometry. Boston, Ginn & Company, 1917. 123 p.
29. Lockwood E. H. A Book of Curves. Cambridge, Cambridge University Press, 1961. 199 p.
30. Tabak J. Geometry. The Language of Space and Form. New York, Facts On File Inc., 2004. 269 p.

References

1. Adamar J. Jelementarnaja geometrija. Chast' I. Planimetrija [Elementary geometry. Part I. Planimetry]. Moskow, Uchpedgiz Publ., 1948. 608 p. (in Russian).
2. Akopyan A. V., Zaslavskiy A. A. Geometricheskie svoystva krivyih vtorogo poryadka [Geometric properties of secondorder curves]. Moscow, MTsNMO Publ., 2007. 136 p. (in Russian).
3. Argunov B. I., Balk M. B. Geometricheskie postroenija na ploskosti [Geometric constructions on the plane]. Moskow, Uchpedgiz, 1957. 268 p. (in Russian).
4. Belotserkovskiy D. L. Krivye vtorogo porjadka na ploskosti [Second-order curves on the plane]. Moskow, Gubkin Russian state University of oil and gas, 2009. 42 p. (in Russian).
5. Berger M. Geometrija [Geometry: translated from French]. Moskow, Mir. Publ. V. 2. 368 p. (in Russian).
6. Vasin S. I., Ivanov V. I. Analiticheskaja geometrija [Analytical geometry]. Moskow, Gubkin Russian state University of oil and gas, 2010. 60 p. (in Russian).
7. Voloshinov D. V. Geometricheskaja laboratorija. Zakladyvaem osnovy [Geometric laboratory. Found the groundwork]. VII Mezhdunarodnaya internet-konferentsiya KGP-2017 [VII international online conference, HACO-2017]. Available at: http://dgng.pstu.ru/conf2017/papers/53. (in Russian).
8. Voloshinov D. V. Geometricheskaja laboratorija. Instrumenty ortogonal'nosti [Geometric laboratory. Tools of orthogonality]. VII Mezhdunarodnaya internet-konferentsiya KGP-2017 [VII international online conference, HACO-2017]. Available at: http://dgng.pstu.ru/conf2017/papers/72. (in Russian).
9. Voloshinov D. V. Geometricheskaja laboratorija. Novyj geometricheskij instrument [Geometric laboratory. New geometric tool]. VII Mezhdunarodnaya internet-konferentsiya KGP-2017 [VII international online conference, HACO-2017]. Available at: http://dgng.pstu.ru/conf2017/papers/60. (in Russian).
10. Voloshinov D. V. Konstruktivnoe geometricheskoe modelirovanie. Teorija, praktika, avtomatizacija [Constructive geometric modeling. Theory, practice, automation]. Saarbrücken, Lambert Academic Publ., 2010. 355 p. (in Russian).
11. Volberg A. O. Osnovnye idei proektivnoj geometrii [Basic ideas of projective geometry]. Moskow-Leningrad, Uchpedgiz Publ., 1949. 188 p (in Russian)..
12. Gil'bert D., Kon-Fossen S. Naglyadnaya geometriya [Visual Geometry]. Moscow, Nauka Publ., 1981. (in Russian).
13. Hirsh A. G. Fokusy algebraicheskih krivyh [Foci of algebraic curves]. Geometriya i grafika [Geometry and Graphics]. 2015. V. 3, pp. 4-17. (in Russian). DOI: 10.12737/14415.
14. Glagolev N. A. Proektivnaja geometrija [Projective geometry]. Moskow, Vysshaya shkola Publ.,1963. 342 p. (in Russian).
15. Dorfman A. G. Optika konicheskih sechenij [Optics of conical sections]. Moskow, Fizmatgiz. Publ., 1959. 32 p. (in Russian).
16. Ignatiev Yu. G., Agafonov A. A. Analiticheskaja geometrija evklidovogo prostranstva [Analytical geometry of Euclidean space]. Kazan: Kazan University Publ., 2014. 204 p. (in Russian).
17.  Korn G., Korn T. 2.4-5. 2.4-5. Harakteristicheskaja kvadratichnaja forma i harakteristicheskoe uravnenie [Characteristic quadratic form and characteristic equation Handbook of mathematics. 4th edition] [Characteristic quadratic form and characteristic equation]. Moskow, Nauka Publ., 1978. P. 64. (in Russian).
18. Korotky V. A., Hmarova L. I. Nachertatel'naja geometrija na jekrane komp'jutera. [Descriptive geometry on the computer screen]. Geometriya i grafika [Geometry and Graphics]. 2013. V. 1, pp. 32–34. (in Russian).
19. Savel'ev Yu. A. Grafika mnimyh chisel [Imaginary number graphics]. Geometriya i grafika [Geometry and Graphics]. 2013. V. 1. I. 1, pp. 22–23. (in Russian). DOI: 10.12737/2079.
20. Chetverukhin N. F. Proektivnaja geometrija [Projective geometry]. Moscow, Uchpedgiz Publ,. 1961. P. 268. (in Russian).
21. Audin M. Geometry. Strasbourg. 2002. 363 p.
22. Busemann H., Paul J. Kelly. Projective geometry and projective metrics. New York, Academic press Inc. Publ., 1962. P. 88.
23. Field P. Projective geometry with applications to engineering. New York, D.Van Nostrand Company. 1923. P. 79.
24. Gallier J. Curves and Surfaces In Geometric Modeling: Theory And Algorithms. Philadelphia, University of Pennsylvania, 2015. 492 p.
25. Herman I. The Use of Projective Geometry in Computer Graphics. Berlin, Springer-Verlag, 1992. 148 p.
26. Boissonnat J-D, MoniqueTeillaud M. Effective Computational Geometry for Curves and Surfaces With 120 Figures and 1 Table. Springer, 2006. 351 p.
27. Jürgen Richter-Gebert. Perspectives on Projective Geometry. A Guided Tour Through Real and Complex Geometry. Berlin, Springer, 2011. 593 p.
28. Lehmer D.N. An Elementary Course In Synthetic Projective Geometry. Boston, Ginn & Company, 1917. 123 p.
29. Lockwood E.H. A Book of Curves. Cambridge, Cambridge University Press, 1961. 199 p.
30. Tabak J. Geometry. The language of space and form. New York, Facts On File Inc., 2004. 269 p.