КОНСТРУКТИВНАЯ ГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ ЧЕТЫРЕХМЕРНОГО ПРОСТРАНСТВА КАК ОСНОВА ДЛЯ РЕШЕНИЯ ЗАДАЧ ЗОНИРОВАНИЯ И ПОЗИЦИОНИРОВАНИЯ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ФАКТОРОВ
Д.В.ВОЛОШИНОВ
Санкт-Петербургский государственный университет телекоммуникаций им. проф.М.А.Бонч-Бруевича (Санкт-Петербург)
denis.voloshinov@yandex.ru
CONSTRUCTIVE GEOMETRIC MODEL OF FOUR-DIMENSIONAL SPACE AS A BASIS FOR SOLVING PROBLEMS OF ZONING AND POSITIONING WITH REGARD TO ADDITIONAL FACTORS
Аннотация
Одной из практически важных задач для проектирования сетей мобильной связи являются задачи позиционирования и зонирования. Геометрические основы этих задач известны под названиями «Поиск ближайшего соседа», построение диаграммы Вороного, триангуляции Делоне, диаграммы Мёбиуса и Аполлония. Известные в настоящее время алгоритмы расчета соответственных геометрических образов являются информационно насыщенными, ресурсоемкими и разработаны только для двумерных и трехмерных пространств. Решение подобных задач в пространствах более высоких размерностях, в которых можно было бы учитывать не только чисто геометрические характеристики физического пространства, но и прочие физические характеристики, затруднено в связи с отсутствием средств для решения задач подобного рода, а также с проблемами, связанными с отсутствием методов визуализации и управления такими моделями. Более того, известные методы не вскрывают проективную сущность этих задач и не касаются проблем существования в них мнимых образов. Однако, как показывают проведенные исследования, все эти задачи имеют единый теоретический фундамент. Их геометрические основания, базируются на понятиях проективной геометрии, преобразовании инверсии, радикальных пространств, представленных в единстве в хорошо известной, но недостаточно исследованной задаче Аполлония. В статье доказано, что задача Аполлония и ее аналоги имеют единый метод решения, в отличие от бытующего представления о том, что данные задачи могут быть решены только отдельными частными способами. Предложенная автором концепция геометрического эксперимента позволила обнаружить многие ранее неизвестные и обсуждаемые в статье закономерности, благодаря проведению множества вычислительных испытаний в системе визуального проектирования геометрических моделей Симплекс. В статье рассматривается пример решения аналога задачи Аполлония для четырехмерного пространства, однако действие алгоритма универсально, и он может быть с равным успехом применен к решению подобных задач в пространствах произвольных размерностей. Полученные результаты демонстрируют возможности методов конструктивного моделирования и многомерной начертательной геометрии в приложении к решению сложных математических задач, определяют тенденции развития систем автоматизации конструктивного геометрического моделирования.
Abstracts
One of the most important tasks for the design of mobile communication networks are the tasks of positioning and zoning. The geometric foundations of these problems are known under the names «Search for the nearest neighbor», the construction of the Voronoi diagram, Delaunay triangulation, the Möbius and Apollonius diagrams. The currently known algorithms for calculating the corresponding geometric images are informationally saturated, resource-intensive and designed only for two-dimensional and three-dimensional spaces. The solution of such problems in spaces of higher dimensions in which it would be possible to take into account not only the purely geometric characteristics of the physical space, but also other physical characteristics, is hampered by the lack of the means to solve problems of this kind, as well as the problems associated with the lack of methods visualization and management of such models. Moreover, known methods do not reveal the projective nature of these problems and do not concern the problems of the existence of imaginary images in them. However, studies show, that all these tasks have a single theoretical foundation. Their geometric bases are founded on the concepts of projective geometry, inversion transformation, radical spaces represented in unity in the well known, but insufficiently researched Apollonius problem. It is proved in the article, that the Apollonius problem and its analogues have a single method of solution, in contrast to the current notion, that these problems can be solved only in individual ways. The concept of the geometric experiment, proposed by the author, made it possible to discover many previously unknown laws, discussed in the article, thanks to the carrying out of numerous computational tests in the system Simplex, developed for visual design of geometric models. In this paper it is considered an example of a solution on the analog of the Apollonius problem for four-dimensional space, but the developed algorithm is universal, and it can be applied with equal success to solving similar problems in spaces of arbitrary dimensions. The obtained results demonstrate the possibilities of constructive modeling methods and multidimensional descriptive geometry in the application to solving complex mathematical problems, determine the trends in the development of automation systems for constructive geometric modeling.
Ключевые слова: мобильная сеть, диаграмма Вороного, научная визуализация; многомерное конструктивное геометрическое моделирование; геометрический эксперимент; проективная геометрия; задача Аполлония; мнимые геометрические образы, позиционирование, зонирование.
Keywords: mobile network, Voronoi Diagrams, scientific visualization, multidimensional constructive geometric modeling, geometric experiment, projective geometry, the problem of Apollonius, imaginary geometric objects, zoning, positioning.
1. Введение
В наши дни трудно назвать область человеческой деятельности, которую бы не затронули информационные технологии. Поэтому приходится с сожалением говорить о том, что до сих пор информатизация почти не затрагивает сферы приложения геометрических знаний, не способствует внедрению методов конструктивной геометрии в прикладные разработки и информационные системы. Геометрическая наука до сих пор не получает должной поддержки разработчиков программных систем.
В чем же кроется причина такого неудовлетворительного положения? Дело в том, что по сей день геометрия воспринимается людьми, как достаточно сложная, рутинная, трудноусваиваемая и даже устаревшая наука, которая не находит себе должного практического применения. Дело дошло до того, что современная геометрия, являясь полноправным разделом математики, оказывается не в состоянии конкурировать с ее цифровыми (аналитическими) методами, к которым приковано всеобщее внимание разработчиков и исследователей, благодаря высокой эффективности реализации таких методов в виде компьютерных программ и систем. Конечно, нельзя не вспомнить о том, что существуют программные и информационные средства и для популяризации геометрических знаний, и даже проведения исследований в различных областях, в которых геометрия играет основополагающую роль. Здесь же следует упомянуть успешные разработки множества систем автоматизации проектирования, обеспечения производственной деятельности, в которых геометрические понятия и средства широко используются для проектирования формы изделий и выполнения сопутствующих расчетов. Однако, при всем совершенстве и разнообразии таких средств, геометрическое моделирование в них используется весьма утилитарно и ограниченно. В этой связи мы даже становимся свидетелями подмены понятий: во многих литературных источниках, посвященных т.н. «геометрическому моделированию» мы можем не обнаружить ни одного чертежа – одни аналитические формулы, что, вообще говоря, должно было бы называться аналитическим моделированием геометрии. То есть происходит подмена философских понятий предмета и метода научной дисциплины. Но ведь по сути геометрическое моделирование – это процесс создания описаний окружающей действительности на языке геометрии, а не аналитики!
Геометрическое моделирование – это совершенно равноправный и универсальный метод научного познания, наряду со всеми другими известными, и, может быть, еще не существующими методами моделирования. В отличие от аналитики, геометрия обладает неоспоримым преимуществом, заключающемся в способности доставлять человеку информацию о моделях окружающего мира через зрительный канал. Геометрия образна и визуальна, и поэтому к ней обращены взоры многих исследователей, стремящихся представить результаты своих достижений в наглядной, доступной для понимания форме. И, без сомнения, это стремление показывает впечатляющие результаты. Однако, сущность геометрии заключается не только в этом. Предоставляя возможность оперирования наглядными образами и представлениями, геометрическая наука позволяет исследовать сложнейшие закономерности мироздания, дает возможность заглянуть в миры, которые недоступны обычному человеческому взору. В том числе, в многомерные миры. Складывается парадоксальная ситуация: с одной стороны, геометрическая интерпретация – это шанс осознать нечто, заглянув туда, где обычным глазом ничего не видно, ощутить то, что не осязаемо. С другой стороны, выстраивание логических умозаключений в геометрии требует специальных знаний, умения мыслить абстрактными образами и, конечно же, тренировки. На пути к овладению этими знаниями немало проблем, и основная из них – это высокая трудоемкость достижения результата.
В частности, одна из проблем – это существование в математических задачах мнимых решений [13, 18], которые относительно легко воспринимаются как результат математических действий, но не находят должного понимания в системе геометрических представлений.
Несмотря на то, что мнимые образы в геометрии не являются чем-то концептуально новым, практическое использование таких образов затруднено, поскольку их отображение на действительной плоскости требует косвенных визуальных интерпретаций и выполнения множества дополнительных операций. Еще в 1847 г. Штаудт в работе [30] сформулировал теорию мнимых элементов применительно к проективной геометрии и предложил, в частности, косвенно отображать мнимые точки четверками действительных точек на прямой линии. Несмотря на действенность такого подхода и принципиальную возможность оперирования мнимыми образами через заменяющие их реперы, практическая целесообразность таких замен может быть оценена по достоинству лишь в узком кругу специалистов, имеющих соответственную геометрическую подготовку. И, следовательно, такому подходу вряд ли найдется место в практике повседневного инженерного проектирования в среде людей, не знакомых со специальными разделами геометрии.
Высокая трудоемкость воплощения теоретических моделей в практически значимые расчетные приложения, недопонимание их сути и, вследствие этого, отсутствие ясного представления о сферах приложения этих моделей к реальному проектированию, в конце концов, влекут за собой и снижение интереса к проведению научных изысканий в области конструктивного геометрического моделирования. Отсюда также проистекает и недостаточное внимание разработчиков САПР и систем автоматизации научных исследований к созданию компьютеризированных инструментов, пригодных для работы с геометрическими объектами мнимой природы.
По изложенным выше причинам рассчитывать на успех в деле разработки конструктивных геометрических моделей, учитывающих и действительные, и мнимые геометрические образы, на основе традиционных методов исполнения и визуализации этих моделей в виде графических схем, не приходится. Нет сомнения в том, что пришло время отказаться от прочно укоренившегося стереотипа, навязывающего понимание науки «геометрия» как системы знаний о действиях, выполняемых с помощью циркуля и линейки. Необходимо перейти к иной парадигме. Средства компьютерного моделирования позволяют создавать и практически применять новые виртуальные инструменты с ранее недоступной исследователям функциональностью, которые способны придать мощный импульс научным изысканиям в области конструктивной геометрии и, соответственно, расширить сферы практического приложения геометрического метода. Более того, и традиционные инструменты в компьютерном исполнении приобретают новые качества. Например, компьютеризированный циркуль относительно несложно наделить способностью проводить не только привычные действительные окружности, но и окружности мнимого радиуса в мнимом центре, причем геометрическая сущность самого действия – проведение окружности – от этого не претерпевает никаких изменений. Этот подход исключительно важен и ценен тем, что геометрия, приобретающая подобные инструменты, в глазах осведомленного практика становится по-настоящему полной и значимой.
Концепция создания виртуальных геометрических инструментов, помимо совершенствования геометрической теории, основанная на понимании геометрических конструкций как преобразователей информации – геометрических машин [4, 10], влечет за собой и развитие нового направления научных исследований. Его предметом являются информационные системы представления данных, выраженных в геометрической форме, и средства управления ими посредством визуального графического интерфейса. Практическим результатом этих исследований должна стать разработка информационных систем, предназначенных для автоматизации представления и приложения геометрических знаний, реализации конструктивных геометрических моделей в виде действующих компьютерных программ, готовых к применению в тех областях человеческой деятельности, в которых визуализация является неотъемлемой частью процессов познания, проектирования и управления. Новые информационные средства позволяют сформулировать и развивать концепцию геометрического эксперимента, предназначенного для проверки научных гипотез и изучения ранее неизвестных свойств геометрических конструкций [7–11].
Одной из практически важных задач для проектирования сетей мобильной связи являются задачи позиционирования и зонирования. Геометрические основы этих задач известны под названиями «Поиск ближайшего соседа», построение диаграммы Вороного, триангуляции Делоне, диаграммы Мёбиуса и Аполлония. Известные в настоящее время алгоритмы расчета соответственных геометрических образов являются информационно насыщенными, ресурсоемкими и разработаны только для двумерных и трехмерных пространств [31, 32]. Решение подобных задач в пространствах более высоких размерностях, в которых можно было бы учитывать не только чисто геометрические характеристики физического пространства, но и прочие физические характеристики, затруднено в связи с отсутствием средств для решения задач подобного рода, а также с проблемами, связанными с отсутствием методов визуализации и управления такими моделями. Более того, известные методы не вскрывают проективную сущность этих задач и не касаются проблем существования в них мнимых образов. Однако, как показывают проведенные исследования, все эти задачи имеют единый теоретический фундамент. Их геометрические основания, базируются на понятиях проективной геометрии, преобразовании инверсии, радикальных пространств, представленных в единстве в хорошо известной, но недостаточно исследованной задаче Аполлония, речь о которой пойдет далее в статье.
Задача Аполлония, рассматриваемая в данной статье как пример, иллюстрирующий высказанные соображения, являет собой исключительно изящный и убедительный образец единства геометрической природы действительных и мнимых образов. Учет этого единства позволяет разработать и применять всего один общий конструктивный алгоритм ее решения, свободный от частных исключений, неизбежно присутствующих в ранее известных алгоритмах.
Впервые задача о сопряжении окружностей была сформулирована и решена Аполлонием Пергским примерно в 220 г. до н. э. Частичное решение задачи Аполлония о построении круга, касающегося трёх данных, Франсуа Виет представил в сочинении Apollonius Gallus (1600) [29]. Как известно, решение Виета не подходит для случая внешних касаний. Жозеф Диас Жергонн в 1816 г. разработал изящное решение этой задачи. Многие аспекты решения данной задачи и ряда смежных проблем приводятся в работах [1–3, 6, 15, 17, 19-26].
В классической постановке задача Аполлония формулируется следующим образом: пусть на плоскости даны три несовпадающие и неконцентрические в парах окружности; требуется построить пару окружностей, сопрягающих три заданные окружности. В плоскости задача имеет четыре различные решения – четыре пары окружностей, сопрягающих заданные. Условие задачи легко распространяется и на пространства больших размерностей. В трехмерном пространстве задача будет сформулирована применительно к сферам. В данной статье мы распространим формулировку задачи на четырехмерное пространство.
Как уже говорилось, теоретически, задача Апполония имеет не только вещественные, но и мнимые решения, которые не удается представить в приемлемой визуальной форме, пригодной для выполнения дальнейших операций над получаемыми мнимыми образами с помощью традиционных инструментальных средств. Позиционные отношения, возникающие между исходными окружностями (или гиперсферами в многомерных случаях), приводят к появлению исключительных ситуаций, при которых построение касательных окружностей (гиперсфер) оказывается невозможным. Более того, сама задача Аполлония, в принципе, может быть поставлена над исходными данными, имеющими мнимую природу, что еще сильнее усугубляет ситуацию. Однако, как уже было сказано ранее, эти исключения обусловлены только инструментальными ограничениями геометрической науки, решения которой принято оформлять в виде чертежей простейшими средствами – циркулем и линейкой. Еще раз подчеркнем, что на сам предмет науки эти ограничения оказывать влияние не могут. Но техническая невозможность оперативной работы с мнимыми геометрическими образами лишает поиск теоретических обобщений, направленных на выявление геометрической сущности данной задачи, практического смысла, не позволяет рассматривать ее как цельное звено единой геометрической системы.
Ниже мы рассмотрим ряд теоретических положений и методов использования компьютерных средств визуализации и проектирования геометрических моделей, которые позволят найти не только общее проективное решение задачи Аполлония, но и в равной степени распространить принцип ее решения на пространства высших размерностей на примере четвертой [5, 12, 14, 27, 28]. Причем для решения задач в многомерных пространствах нам понадобятся только средства плоской геометрии. В рассматриваемых алгоритмах будут учтены и мнимые решения, и возможность задания в качестве исходных данных объектов с чисто мнимыми и комплексными значениями. Проектирование и исследование алгоритмов, а также визуальное сопровождение этого процесса осуществляется в среде системы конструктивного геометрического моделирования Симплекс [9, 10]. Изучение теоретического материала, представленного в статье, предполагает базовое знакомство читателя с основами проективной геометрии [14, 16] и теорией функции комплексного переменного.
2. Теоретические предпосылки решение аналогов задачи Аполлония на примере двумерного пространства
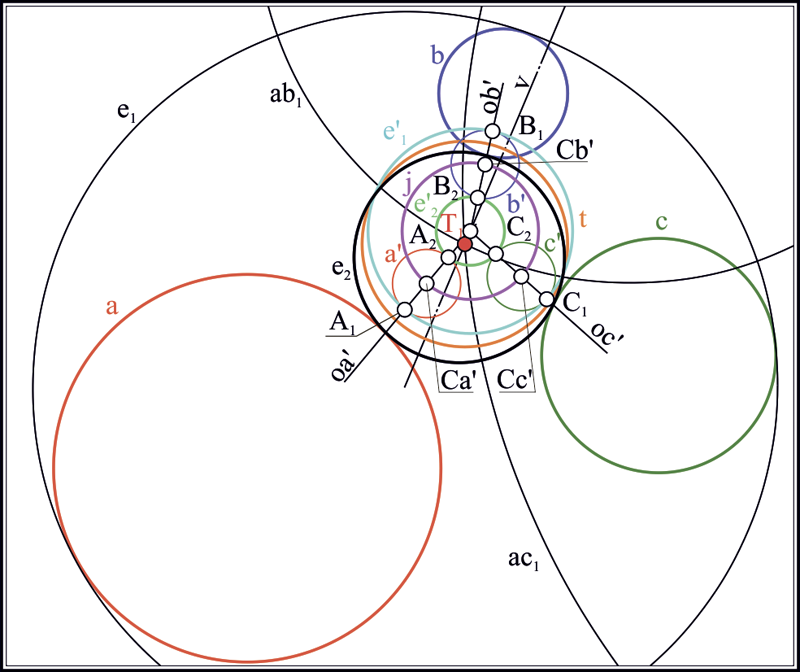
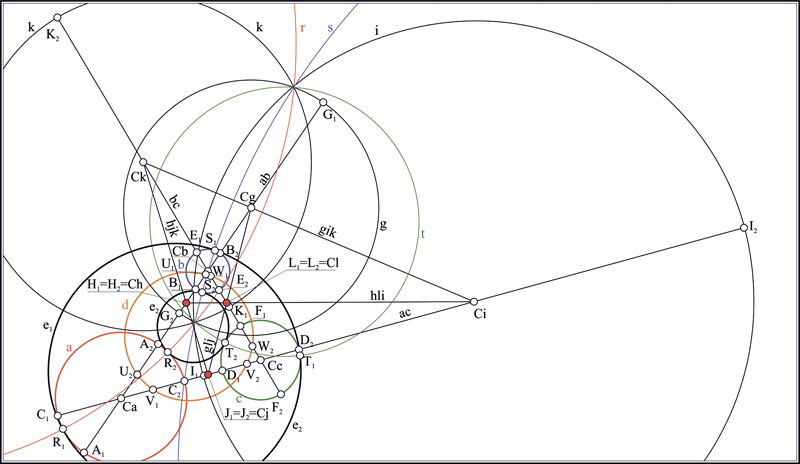
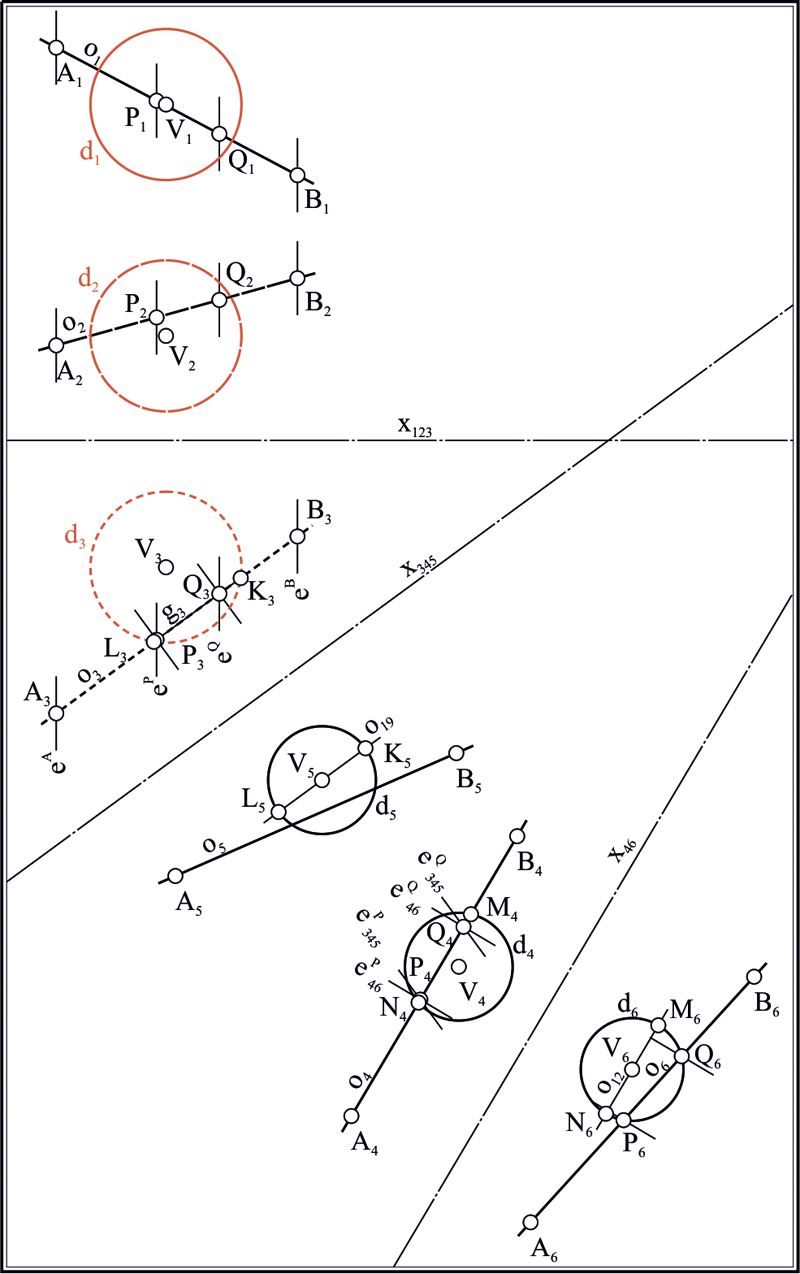
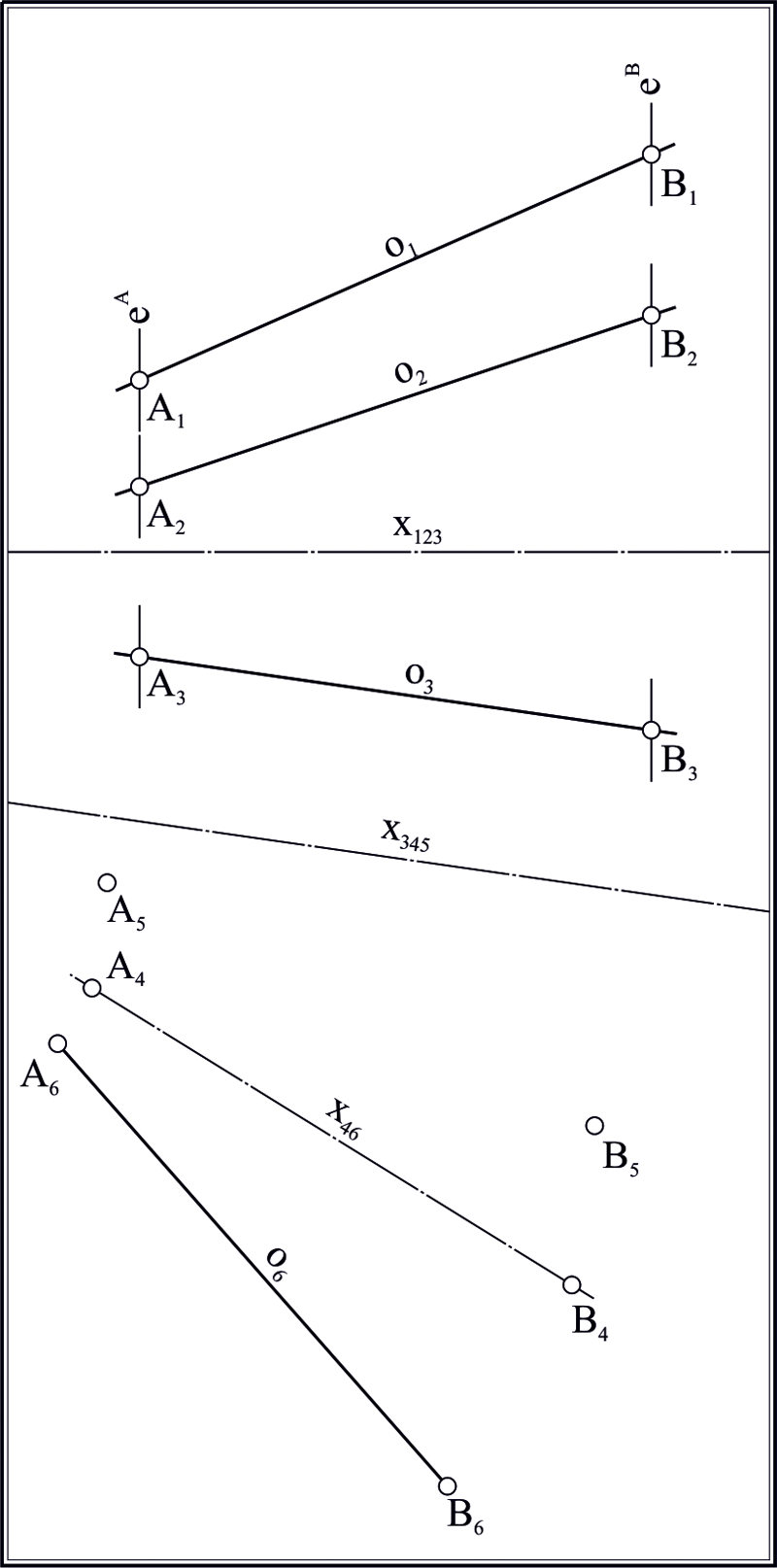
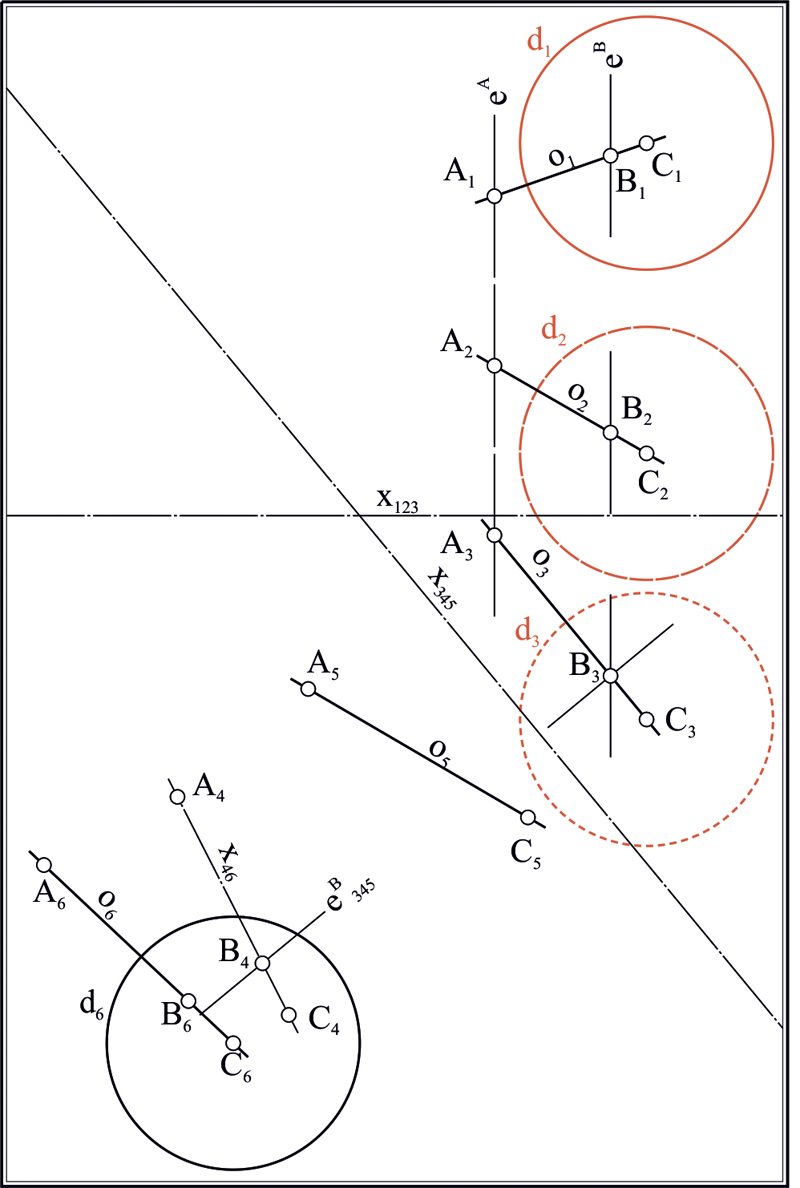
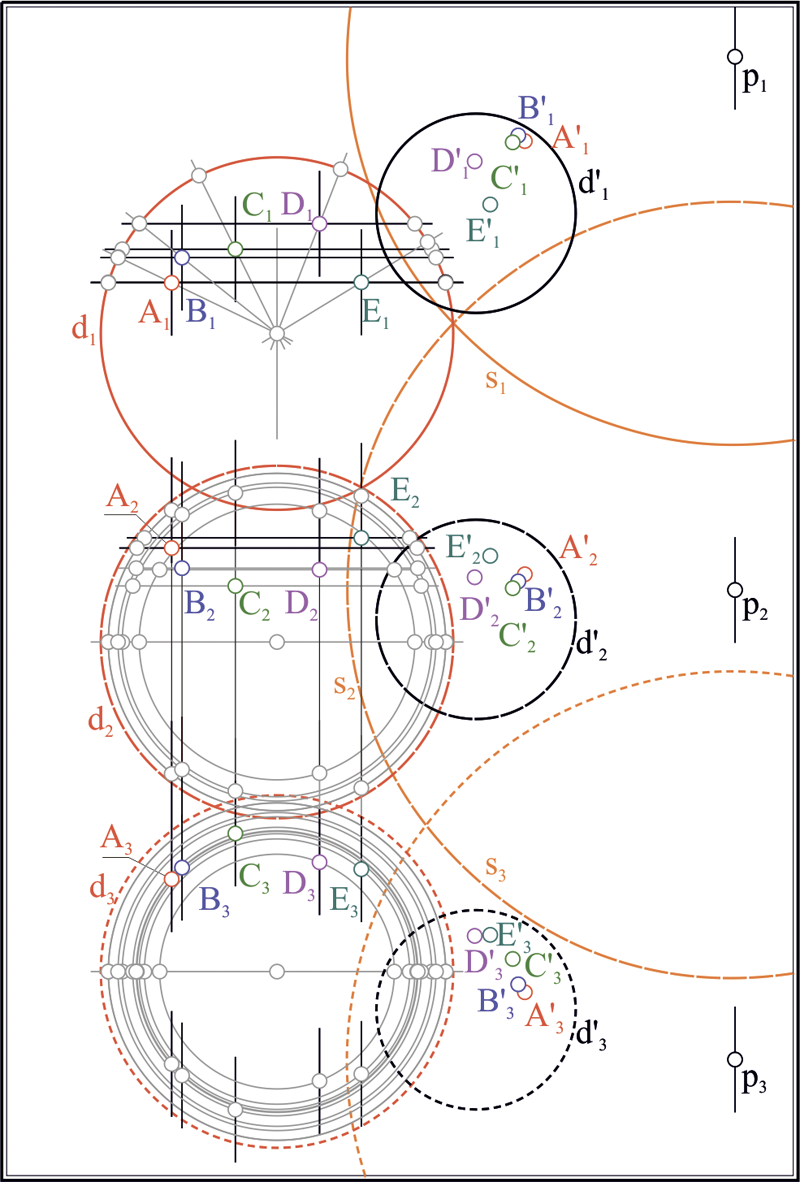
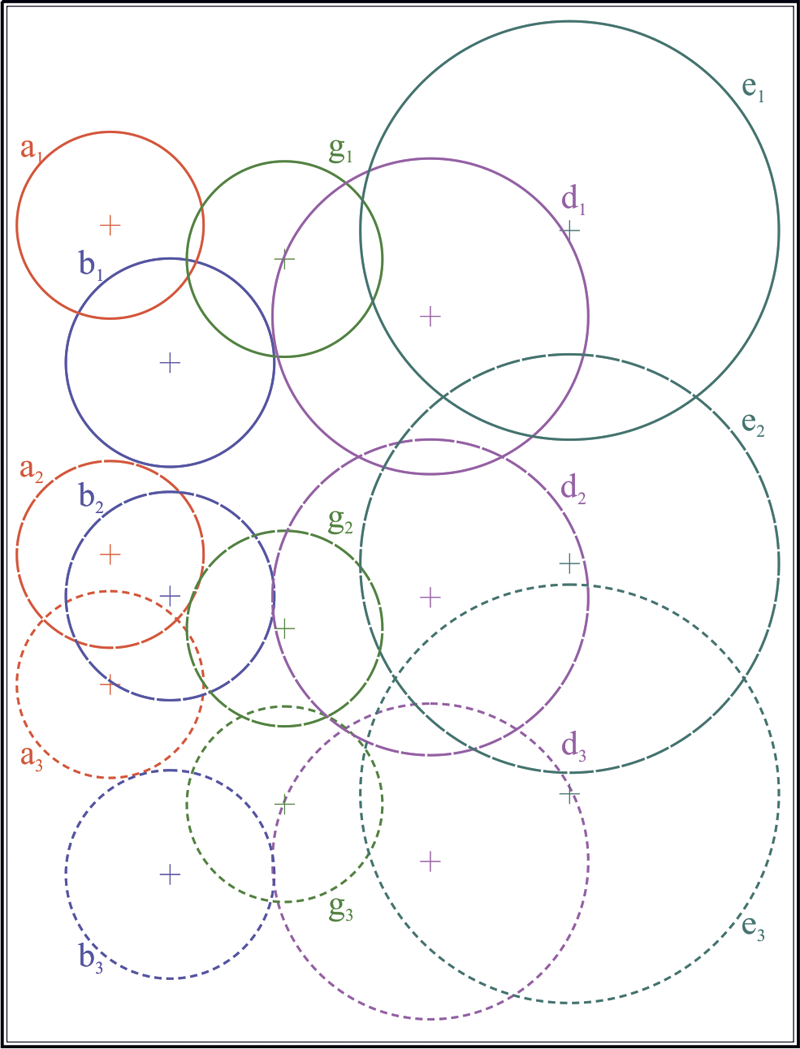
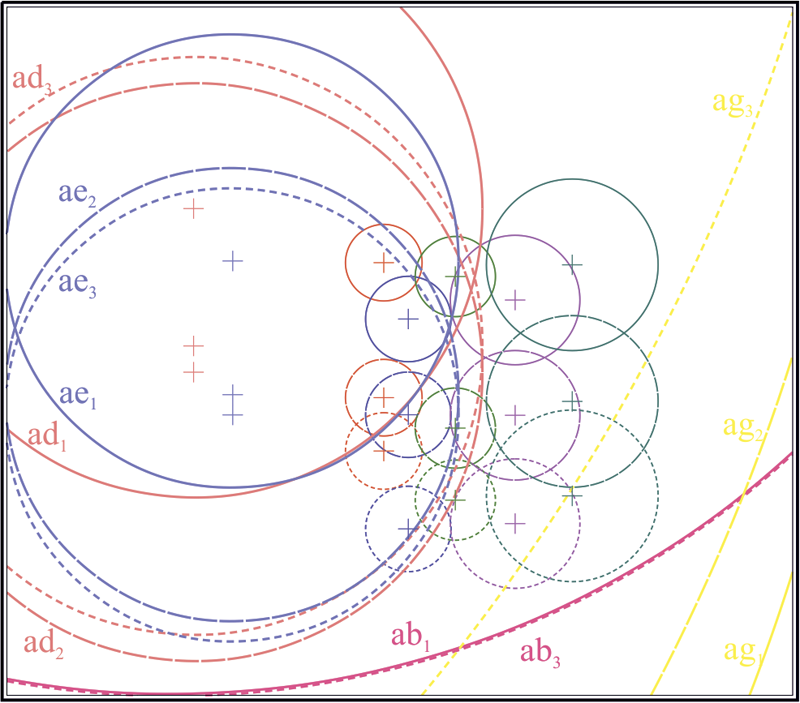
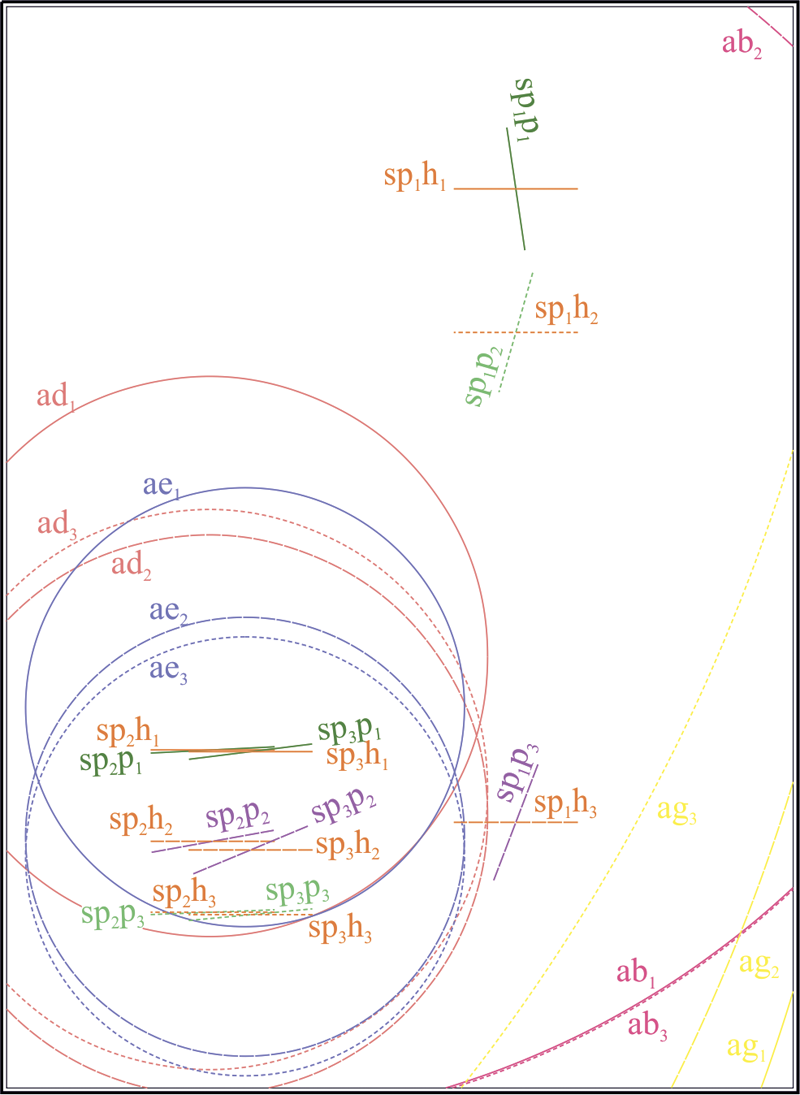
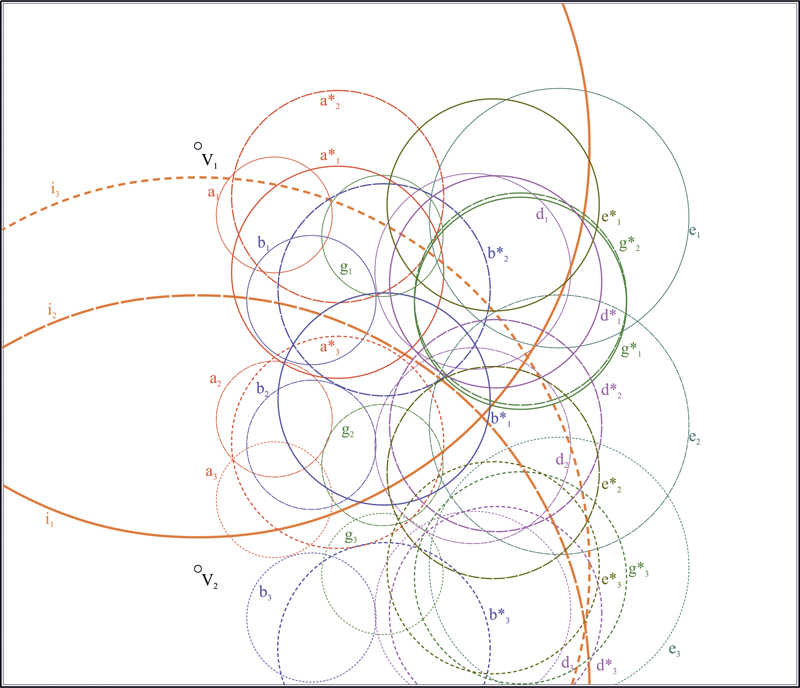
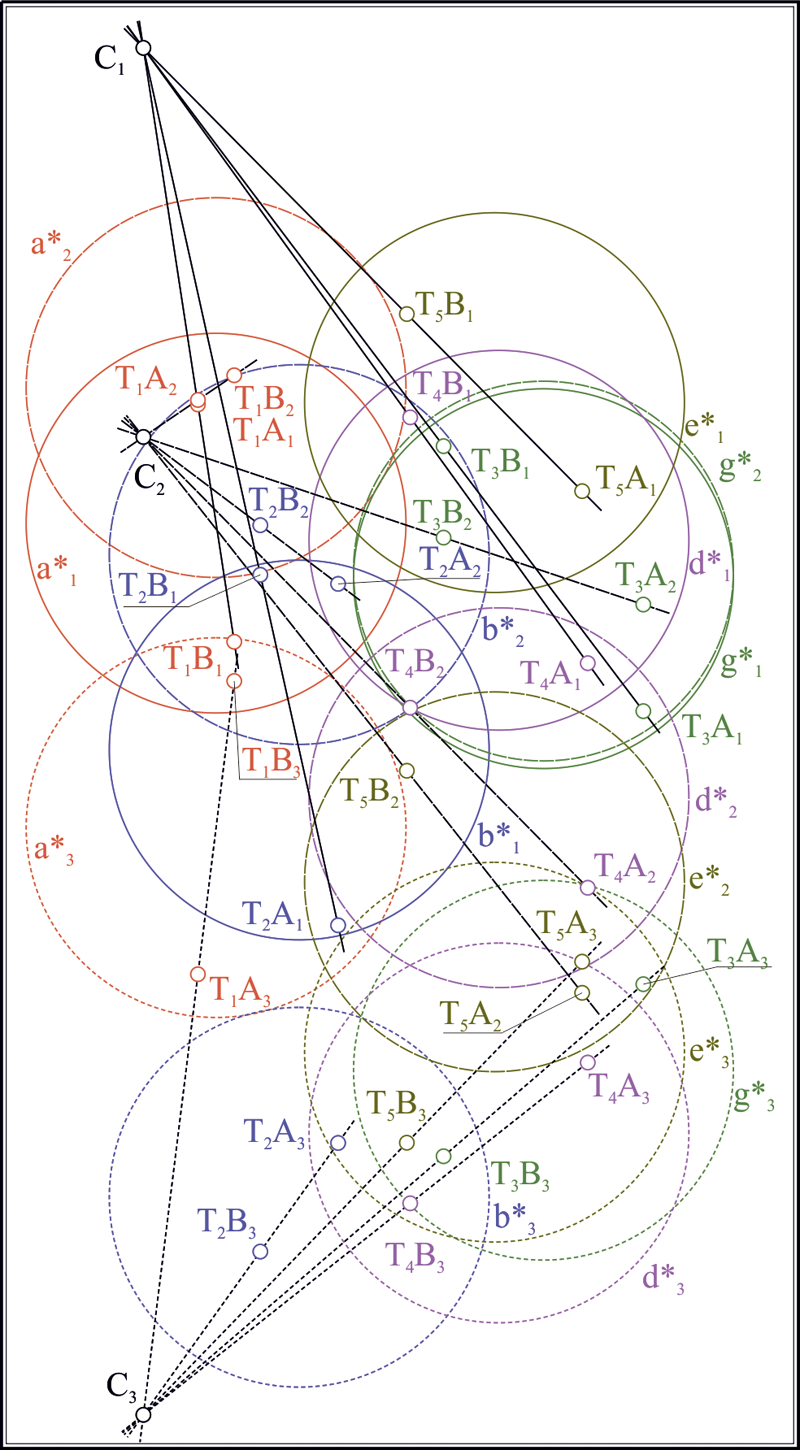
Пусть на плоскости заданы три произвольные (но не концентрические в парах) окружности , и . Найдем центры этих окружностей , и . Построим треугольник, взяв полученные точки за вершины. В предположении, что стороны треугольника , , являются бесконечными прямыми, пересечем стороны с окружностями, через центры которых они проходят: , , , , , . Определим на прямых три инволюции [14, 16]: , и . Найдем двойные точки инволюций ; ; . Выбрав любые три точки из полученных шести, построим на них окружность . Окружность является ортогональной к исходным окружностям , и . Воспользуемся теперь следующими инволюциями, определенными точками пересечения окружностей с соответственными сторонами треугольника. Определим их: , , , , , . Построим двойные точки инволюций: , , , , , . Каждая пара двойных точек, взятых как диаметральные, задает окружности (вещественные и/или мнимые): , , , , , . Найдем центры полученных окружностей: , , , , , . На этих точках построим четыре оси подобия окружностей: , , , . Продемонстрируем действие алгоритма построения пары окружностей, касательных к заданным окружностям , и на примере использования оси подобия . Остальные решения могут быть легко получены заменой оси подобия на необходимую. Будем считать ось подобия окружностью бесконечно большого радиуса. Проведем три окружности перпендикулярно к , и каждой из исходных окружностей , и . : , , ; : , , ; : , , . Найдем точки пересечения полученных окружностей с соответствующими им исходными окружностями: , , . Соединив полученные точки, получаем искомые окружности , (рис. 1). Порядок выбора точек требует некоторых пояснений. Окружность является окружностью инверсии для только что построенных окружностей и . Центр этой окружности является радикальным центром системы окружностей , и . Пары точек , и расположены на прямых, проходящих через радикальный центр и разделяются окружностью . Вследствие этого, перечисленные точки могут быть упорядочены, и точкам, находящимся в единой области, разграниченной окружностью , должен быть предписан одноименный индекс. Тогда соединение точек в окружность подчинено следующему правилу: если центры сопрягаемых окружностей находятся в общей полуплоскости, разграниченной осью подобия окружностей, то окружности сопряжения проходят через точки с одноименными индексами. Если какая-либо из окружностей имеет центр, расположенный в противоположной полуплоскости, то индекс точки, через которую проходит сопрягаемая окружность, противоположен индексам точек, соответствующих окружностям противоположной полуплоскости.
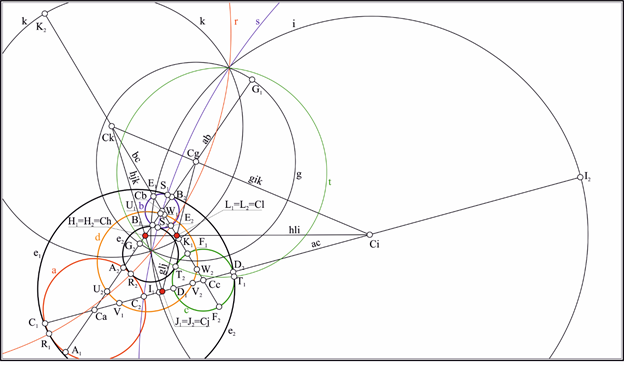
Рис. 1. Геометрическая модель, вскрывающая проекционный характер решения задачи Аполлония
Несмотря на логическую правомерность приведенных утверждений, применение алгоритма выявления троек точек, определяющих касательные окружности, сопряжено с выполнением ряда усложненных операций, в особенности в тех случаях, когда в операциях участвуют объекты с комплексными значениями. Рассмотрим преобразование геометрической конструкции задачи, позволяющей свести операцию селекции точек к сравнению всего двух расстояний. Для решения этой задачи сформулируем и докажем вспомогательную лемму.
Лемма:
На плоскости даны две окружности и . Пусть также центр некоторой окружности находится на окружности , переводящей в индуцируемом ею преобразовании инверсии и друг в друга. Тогда образы и окружностей и в этом преобразовании имеют одинаковый радиус (рис. 2). Вначале рассмотрим конструкцию более общего вида: на плоскости имеются две окружности и ; построим окружности инверсии , переводящие окружности и друг в друга.
Рис. 2. Принцип получения окружностей равного радиуса в преобразовании инверсии; плоская модель
Выберем на плоскости произвольную окружность (рис. 3). Преобразуем в инверсии, индуцированной окружностью , окружности и , а также производные от них окружности и . В результате будут получены образы: , , , . Поскольку инверсия является конформным преобразованием, в образах транзитивно сохранится отношение инверсии , , ,
Рис. 3. Геометрическая схема, поясняющая принцип получения образов исходных окружностей относительно произвольной окружности в плоскости
Пусть теперь окружность расположится так, что ее центр будет находиться на окружности . В этом случае окружности и также переходят в окружности , , а окружность переходит в прямую , так как она ( ) проходит через центр окружности по условию задачи. Поэтому прямая выполняет функции окружности инверсии, переводящей в и наоборот, но в этом случае она является также и осью симметрии этих окружностей, следовательно, преобразование окружностей в возможно только в том случае, если радиусы этих окружностей равны (рис. 4). Лемма доказана.
Рис. 4. Геометрическая схема к доказательству равенства радиусов образов окружностей в преобразовании инверсии в соответствии с условиями леммы; модель
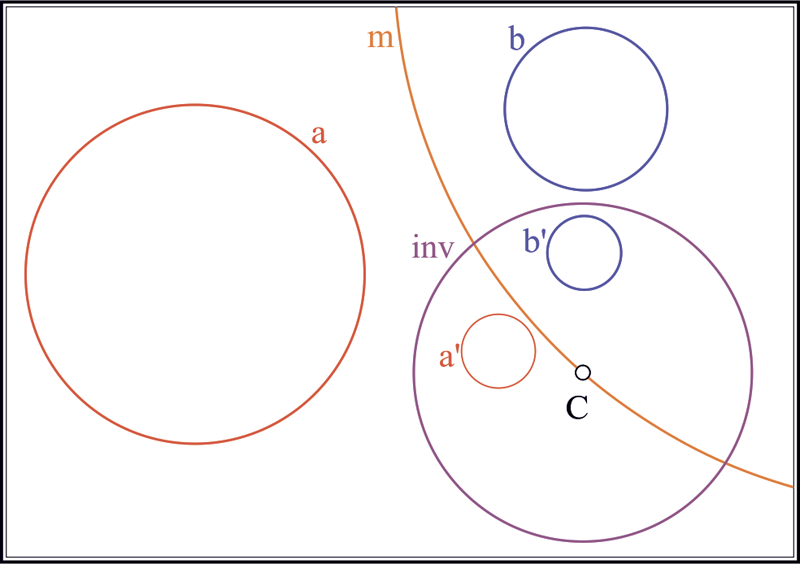
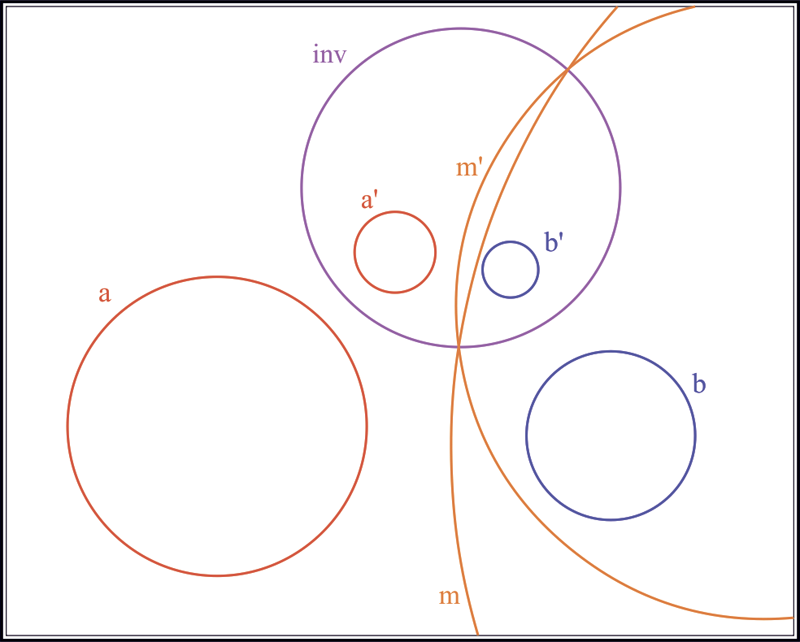
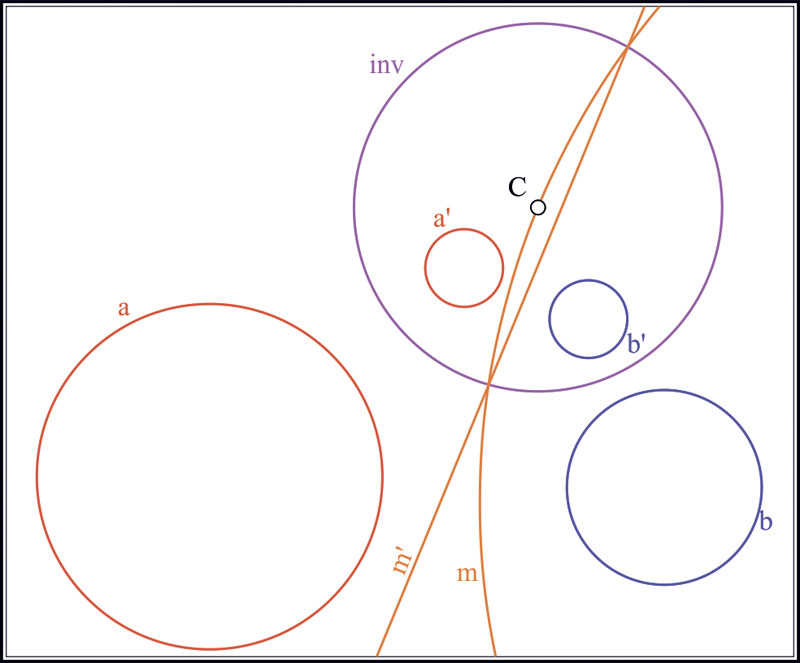
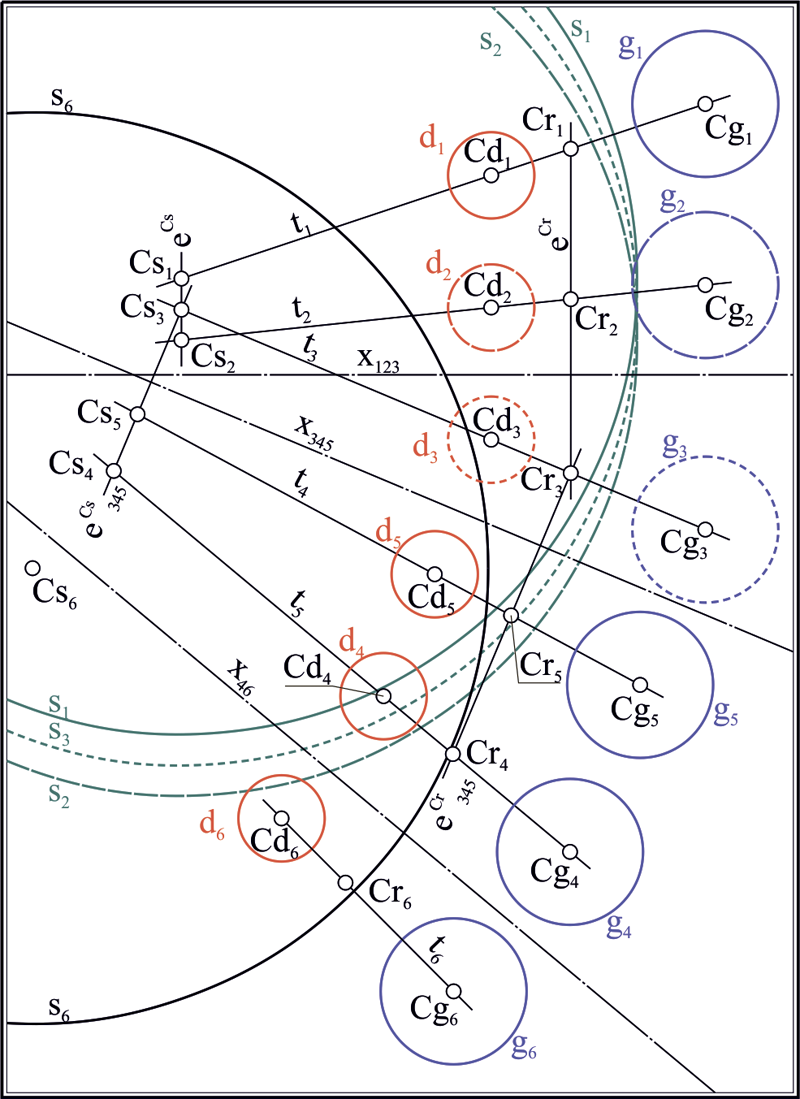
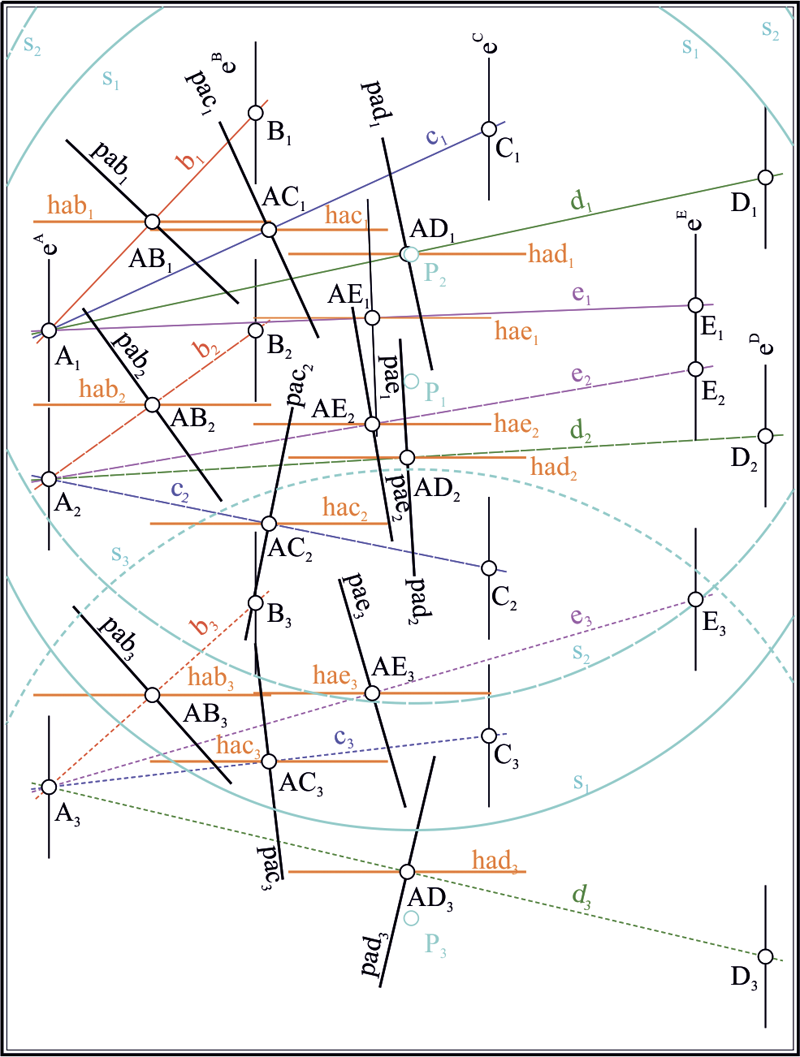
Вернемся к задаче Аполлония. Пусть теперь даны три окружности , и (рис. 5). Построим окружности инверсии для пары : и для пары : . Построим радикальную ось , например, окружностей и . Найдем точки пересечения радикальной оси с одной из окружностей, например
Рис. 5. Геометрическая схема, поясняющая способ нахождения окружности инверсии, преобразующей три произвольные окружности в окружности равного радиуса, решение задачи Аполлония в образах и обратное преобразование промежуточного решения; модель
Представленный алгоритм не претерпевает принципиальных изменений в тех случаях, когда для нахождения остальных решений задачи во взаимодействие вступают незадействованные в приведенном примере окружности инверсии (возможно, мнимые), порожденные от пар исходных окружностей. Так или иначе, задача будет сведена к построению трех (возможно, мнимых) окружностей равного радиуса, что позволит разграничить точки в образах сопряжений и, получив промежуточное решение, преобразовать его к естественному виду исходной задачи. Совершенно по тому же принципу могут быть решены и аналоги задачи Аполлония, сформулированные в терминах многомерного пространства. На рис. 6 представлена обобщенная блок-схема алгоритма решения этой задачи для пространства произвольной размерности. Разумеется, под термином «сфера» следует понимать гиперсферу соответственной размерности, в том числе окружность, сферу, гиперсферу и т.д.
Рис. 6. Блок-схема алгоритма решения аналога задачи Аполлония в пространстве произвольной размерности
Таким образом, задачу Аполлония можно считать полностью решенной. Достоинство представленного метода заключается в том, что решение этой задачи не зависит от расположения исходных окружностей и всегда исполняется по одному и тому же алгоритму. Более того, алгоритм инвариантен к виду исходных данных, он оказывается пригодным для решения задачи и в том случае, если исходные окружности не являются вещественными, то есть они могут обладать мнимыми радиусами и центрами в любых комбинациях. Далее в статье будет представлено решение задачи, сформулированное в терминах четырехмерного пространства. Для ее геометрического представления будут использованы три проекционные модели:
3. Алгоритмическое обеспечение для решения аналога задачи Аполлония в четырехмерном пространстве
3.1. Алгоритм построения гиперсфер инверсии двух гиперсфер (alg1)
Пусть имеются две гиперсферы
Построим в шестом поле проекции очерки сфер
Рис. 7. Схема геометрической машины, предназначенной для построения сфер инверсии для двух произвольных сфер на модели
3.2. Алгоритм построения радикальных пространств двух гиперсфер (alg2)
Пусть имеются две гиперсферы
Первая прямая
Вторая прямая:
Входными параметрами алгоритма являются очерки проекций двух гиперсфер
Рис. 8. Схема геометрической машины, предназначенной для построения радикального пространства двух произвольных гиперсфер на модели
3.3 Алгоритм построения прямой линии от пересечения трех трехмерных пространств в четырехмерном пространстве (alg3)
Пусть имеется три трехмерные пространства
Задача разбивается на два этапа. Этап первый: как известно, в четырехмерном пространстве два трехмерных пространства пересекаются по плоскости. Следовательно, выбрав две пары трехмерных пространств
Поскольку каждая из полученных плоскостей инцидентна с одним и тем же трехмерным пространством
Этап второй: понизив размерность пространства до третьего, найдем на модели
Входными параметрами описанного алгоритма являются проекции реперов трех трехмерных пространств
Рис. 9. Схема геометрической машины, предназначенной для построения линии пересечения трех трехмерных пространств, расположенных в четырехмерном пространстве, на модели
3.4. Алгоритм построения точки пересечения гиперсферы и прямой линии (alg4)
Пусть в четырехмерном пространстве заданы гиперсфера и прямая линия . Найдем пару точек, являющихся результатом пересечения гиперсферы и прямой (рис. 10).
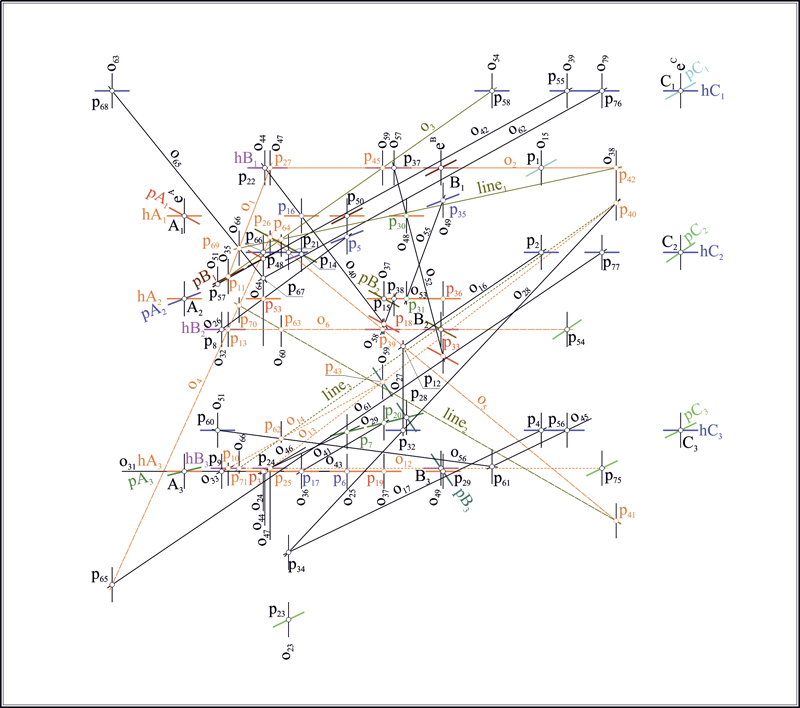
На проекционном чертеже гиперсфера задана тремя очерками – окружностями . Прямая линия задана тремя проекциями , , . Проведем через прямую линию проецирующее трехмерное пространство таким образом, чтобы в третьем поле она отобразилась следом, совпадающим с проекцией прямой . Такое пространство высекает из гиперсферы сферу , радиус которой равен длине хорды , образованной точками пересечения прямой и окружности : .
Выбрав произвольно положение горизонтальной оси , перейдем к новой системе проекций, в которой прямая представлялась бы линией уровня, для чего выберем новую ось проекций . Указав на прямой две произвольные, но не совпадающие точки и : , , ; , , , переведем в новую систему исходную прямую с получением проекций , и построим в этих проекциях очерки и сферы-сечения . В полученной системе проекций задачу можно рассматривать, как трехмерную, то есть искать точки пересечения прямой, представленной проекциями и и сферы , заданной очерками и . Вновь прибегнем к понижению размерности задачи, назначая новую ось проекций , параллельной к одной из проекций прямой, например, к прямой , . Проводя через прямую проецирующую плоскость таким образом, чтобы ее след совпал с проекцией : , определим длину хорды ; , что позволит в шестом поле построить окружность-сечение с центром в точке и диаметром, равным длине хорды . Решение задачи в шестом поле очевидно: . Для нахождения точек пересечения гиперсферы и прямой линии в исходных полях, выполним обратный переход по построенным системам проекций, последовательно переводя точки , по линиям связи на соответственные проекции прямой . В итоге получаем две тройки точек – проекции искомых точек пересечения гиперсферы с прямой линией: , , и , , , являющиеся решением поставленной задачи. Обозначим входные и выходные параметры алгоритма. Его входом являются окружности-очерки , , гиперсферы и проекции , , прямой линии , а выходом проекции двух точек: и .
Рис. 10. Схема геометрической машины, предназначенной для построения точек пересечения прямой линии с гиперсферой на модели
3.5. Алгоритм нахождения расстояния между двумя точками в четырехмерном пространстве (alg5)
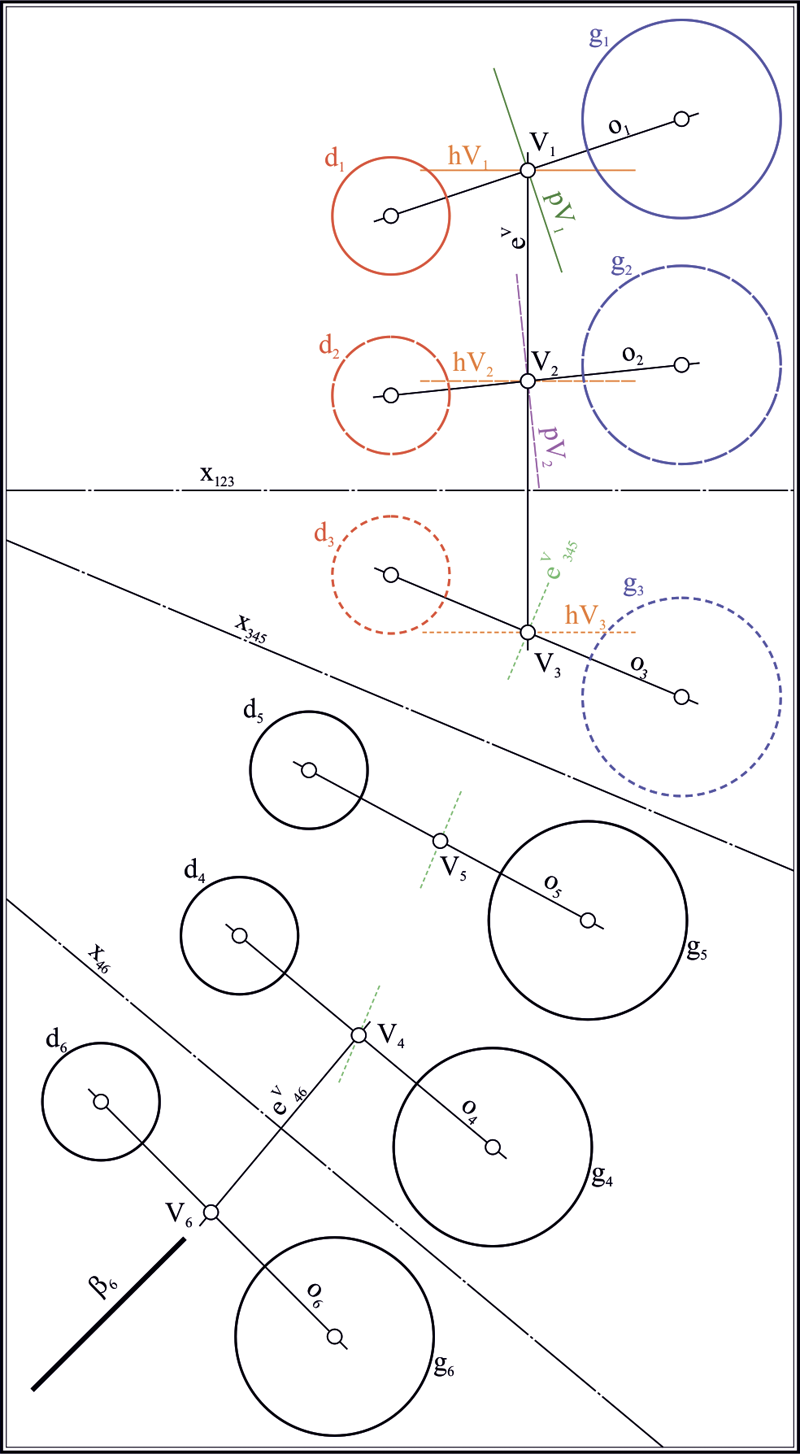
Пусть в четырехмерном пространстве заданы две точки и (рис. 11). Для определения расстояния между этими точками необходимо построить систему плоскостей проекций таким образом, чтобы в ней прямая, соединяющая точки и , стала линией уровня.
Выберем произвольно положение горизонтальной оси проекций , а новую ось проведем параллельно отрезку : . Измеряя превышения точек , , над осью , отложим их по соответственным линиям связи в новые поля для получения проекций , , , . Для сведения задачи к трехмерному случаю следующую ось проекций построим параллельно одному из полученных отрезков или , например, . Тогда, отложив превышения точек , по соответственным линиям связи в шестое поле, получаем проекции , . Поскольку в последней системе плоскостей проекций с осью отрезки и моделируют линию уровня и , то расстояние между исходными точками и может быть считано с шестой проекции как длина отрезка . Входом алгоритма являются проекции точек и , выходом – величина расстояния между этими точками.
Рис. 11. Схема геометрической машины, осуществляющей нахождение расстояния между двумя точками в четырехмерном пространстве; модель
3.6. Алгоритм построения гиперсферы по пяти точкам (alg6)
Пусть имеются четыре точки, расположенные в четырехмерном пространстве: , , , и . Требуется провести сферу через эти пять точек (рис. 12).
Для решения задачи соединим отрезками прямой точку с остальными исходными точками , , и : : , , ; : , , ; : , , и : , , .
Построим в средних точках , и полученных отрезков четыре ортогональных трехмерных пространства, соответственно: , , , . Рассмотрим построение ортогонального пространства на примере моделирования пространства . Первая прямая репера этого пространства должна отвечать следующим условиям: , ; , ; .
Вторая – , , ; , .
Третья – , ; , ; , .
Моделирование реперов пространств , и осуществляется аналогично. Центр искомой гиперсферы находится, как точка пересечения четырех трехмерных пространств , , и , а радиус, как расстояние между полученной точкой и любой из исходных точек, например, (алгоритм alg5). Задача нахождения точки пересечения сводится к двойному применению алгоритма alg3, позволяющему найти две прямые от пересечения двух троек пространств , , и , , . Пересекая полученные прямые, находим центр искомой гиперсферы .
Перечислим входные и выходные параметры синтезированного алгоритма. Его входом являются проекции пяти точек , , , и , а выходом – проекции очерков искомой сферы .
Рис. 12. Схема геометрической машины, осуществляющей построение гиперсферы по пяти точкам; модель
3.7. Алгоритм построения точки в инверсии относительно гиперсферы (alg7)
Пусть имеется точка и гиперсфера , заданная очерками (рис. 13). Соединим центр сферы и точку прямой линией , , и построим систему плоскостей проекций, в которой линия займет положение линии уровня по алгоритму, аналогичному алгоритму определения расстояния между точками. Поскольку в шестом поле проекция отображается в натуральную величину, то положение шестой проекции точки-образа исходной точки в инверсии относительно гиперсферы может быть определено в результате решения задачи о преобразовании точки в инверсии относительно очерка в плоской постановке. Для окончательного решения задачи остается лишь определить положение проекций точек , , которые несложно построить, восстановив необходимые проекции по линиям связи на соответственных проекциях прямой . Входными параметрами данного алгоритма являются проекции точки и очерки сферы ; выходным параметром – проекции , , точки-образа точки .
Рис. 13. Схема геометрической машины, осуществляющей преобразование точки в инверсии относительно гиперсферы; модель
3.8. Алгоритм построения гиперсферы в инверсии относительно другой гиперсферы (alg8)
Пусть имеется гиперсфера , которую требуется преобразовать в инверсии относительно гиперсферы (рис. 14). Для решения задачи выберем на гиперсфере пять произвольных несовпадающих точек , , , и , каждую из которых преобразуем в инверсии в точки , , , и относительно гиперсферы в соответствии с алгоритмом alg7. Воспользовавшись алгоритмом построения гиперсферы по пяти точкам (alg6) найдем искомый образ исходной сферы . Таким образом, входными параметрами алгоритма являются сфера-прообраз и сфера инверсии ; выходным – сфера-образ .
Рис. 14. Схема геометрической машины, осуществляющей преобразование сферической поверхности в инверсии относительно сферы; модель
3.9 Общее решение задачи
Пусть заданы пять гиперсфер: , , , и (рис. 15).
Рис. 15. Исходные данные задачи; модель
Используя алгоритм alg1, построим гиперсферы инверсии для пар гиперсфер, образованных общей гиперсферой и остальными исходными гиперсферами: , , , (рис. 16).
Рис. 16. Результат поиска гиперсфер, задающих инверсии в парах гиперсфер , , и ; модель
Применяя алгоритм alg2, определим радикальные пространства для пар сфер , и и с помощью алгоритма alg3 найдем линию их пересечения (рис. 17).
Рис. 17. Результат построения трех радикальных пространств инверсионных гиперсфер; модель
Построим точки пересечения и найденной линии с любой из гиперсфер инверсии, например, с гиперсферой , реализуя алгоритм alg4. (рис. 18)
Рис. 18. Построение радикальной оси трех инверсионных гиперсфер и точек пересечения полученной прямой с инверсионными гиперсферами; модель
Выбрав любую из полученных точек, например , построим с центром в этой точке гиперсферу произвольного радиуса. Данная гиперсфера обладает свойством преобразовывать в инверсии исходные гиперсферы задачи в гиперсферы-образы одинакового радиуса. Пользуясь алгоритмом alg8 выполним это преобразование: , , , , (рис. 19).
Рис. 19. Задание гиперсферы
Поскольку центры гиперсфер , , , и известны, не составит особого труда построить вспомогательную гиперсферу , проходящую через эти пять точек, воспользовавшись алгоритмом alg6, найти ее центр и ее радиус.
Проведем через полученный центр и центры гиперсфер , , , и прямые линии и найдем с помощью алгоритма alg4 точки их пересечения с соответственными гиперсферами: , , (рис. 20).
Рис. 20. Поиск точек касания двух не пересекающихся по действительным сферам гиперсфер к пяти гиперсферам одинакового радиуса; модель
Полученные точки есть точки касания двух гиперсфер пяти гиперсфер-образов , , , и равного радиуса. Распределив эти точки в два множества таким образом (используя алгоритм alg5), чтобы расстояние от каждой точек первого множества до центра было больше радиуса гиперсферы , а от точек второго – меньше этого радиуса, построим на двух пятерках точек две гиперсферы и , касательные к , , , и (алгоритм alg8). Тогда образы и этих гиперсфер в преобразовании инверсии относительно гиперсферы будут касательными к исходным гиперсферам , , , и (рис. 21).
Рис. 21. Окончательный результат решения задачи; модель
Поставленная задача решена.
4. Заключение
В результате проведенных исследований были получены следующие результаты:
Разработана единая конструктивная геометрическая модель, позволяющая решать задачу Аполлония без известных исключений и учитывающая как действительные, так и мнимые значения исходных данных и получаемых результатов.
Впервые представлено полное конструктивное решение аналога задачи Аполлония для четырехмерного пространства.
Представлена методика и продемонстрировано ее применение для визуального синтеза компьютерных программ, основанных на принципах конструктивного геометрического моделирования и позволяющих применять эти модели в прикладных областях, нуждающихся в геометрической интерпретации и визуализации данных, а также управления ими через визуально-графический интерфейс.
Продемонстрировано применение средств геометрического моделирования для решения задачи, которая трудно формализуется в аналитической форме без привлечения геометрической теории.
Представленные чертежи демонстрируют высокую информационную насыщенность геометрических моделей, что доказывает невозможность ведения исследовательской деятельности и практических внедрений ее результатов без применения средств автоматизации соответствующих исследований.
Исследование геометрических моделей и конструкций приобретает ясно очерченный смысл, поскольку методика визуального проектирования позволяет без каких-либо дополнительных усилий и затрат практически претворять результаты исследований в виде действующих программ и аппаратных устройств, формировать востребованную систему геометрических знаний.
Продемонстрированы возможности системы конструктивного геометрического моделирования Симплекс в деле проектирования конструкций геометрических машин.
Список используемых источников
- Viete F. Apollonius Gallus. Paris: Le Clerc, 1600. Von Staudt G.K.C. Geometrie der Lage. Nürnberg: Verlag von Bauer und Raspe, 1847.
- Адамар Ж. Элементарная геометрия. Часть первая. Планиметрия. M.: Учпедгиз, 1948. 608 с.
- Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости. М.: Учпедгиз, 1957. 267 с.
- Бакельман И.Я. Инверсия. М.: Наука, 1966. 79 с.
- Вальков К.И. Введение в теорию моделирования. Л.: ЛИСИ, 1974. 152 с.
- Волков В.Я., Юрков В.Ю., Панчук К.Л., Кайгородцева Н.В. Курс начертательной геометрии на основе геометрического моделирования: учебник. Омск: Изд.-во СибАДИ, 2010. 253 с.
- Волошинов Д.В. Алгоритм решения задачи Аполлония на основе построения ортогональных окружностей // 26-я Международная научная конференция. Россия, Нижний Новгород. 2016. С. 284–288.
- Волошинов Д.В. Геометрическая лаборатория. Закладываем основы // Качество графической подготовки: проблемы, традиции и инновации. Материалы VII международной Интернет-конференции. Пермь. 2017.
- Волошинов Д.В. Геометрическая лаборатория. Инструменты ортогональности // Качество графической подготовки: проблемы, традиции и инновации. Материалы VII международной Интернет-конференции. Пермь. 2017.
- Волошинов Д.В. Инструмент для геометрического эксперимента. Каким ему быть? // Проблемы качества графической подготовки: традиции и инновации. Материалы V международной Интернет-конференции. Пермь. 2015.
- Волошинов Д.В. Конструктивное геометрическое моделирование. Теория, практика, автоматизация. Saarbrücken: Lambert Academic Publishing, 2010. 355 c.
- Волошинов Д.В. Геометрическая лаборатория. Новый геометрический инструмент // Качество графической подготовки: проблемы, традиции и инновации: Материалы VII международной Интернет-конференции. Пермь. 2017.
- Вольберг О.А. Основные идеи проективной геометрии. М.: Учпедгиз, 1949. 188 с.
- Гирш А.Г. Наглядная мнимая геометрия. М.: Маска, 2008. 216 с.
- Глаголев Н.А. Проективная геометрия. М.: Высшая школа, 1963. 342 с.
- Жижилкин И.Д. Инверсия. М.: Изд-во МЦНМО. 2009. 72 с.
- Короткий В.А. Центральное проецирование двух компланарных коник в две окружности// Проблемы качества графической подготовки. Материалы IV международной Интернет-конференции. Пермь. 2014.
- Курант P., Роббинс Г. Что такое математика? (Элементарный очерк идей и методов). М.: МЦНМО, 2001. 568 с.
- Пеклич В.А. Мнимая начертательная геометрия. М.: Издательство Ассоциации строительных вузов. 2007. 104 с.
- Сальков Н.А. Свойства циклид Дюпена и их применение. Ч. 1. // Геометрия и графика. 2015. Т. 3. № 1. С. 16–25.
- Сальков Н.А. Свойства циклид Дюпена и их применение. Ч. 2. // Геометрия и графика. 2015. Т. 3. № 2. С. 9–22.
- Сальков Н.А. Свойства циклид Дюпена и их применение. Ч. 3: сопряжения. // Геометрия и графика. 2015. Т. 3. № 4. С. 3–14.
- Сальков Н.А. Свойства циклид Дюпена и их применение. Ч. 4: приложения. // Геометрия и графика. 2016. Т. 4. № 1. С. 21–33.
- Сальков Н.А. Способы задания циклид Дюпена // Геометрия и графика. 2017. Т. 5. № 3. С. 11–24.
- Сальков Н.А. Циклида Дюпена и ее приложение: монография. М.: ИНФРА-М. 2016. 141 с.
- Сальков Н.А. Циклида Дюпена и кривые второго порядка. Ч. 1. // Геометрия и графика. 2016. Т. 4. № 2. С. 19‑28.
- Сальков Н.А. Циклида Дюпена и кривые второго порядка. Ч. 2. // Геометрия и графика. 2016. Т. 4. № 3. С. 17‑28.
- Филиппов П.В. Начертательная геометрия многомерного пространства и ее приложения. М.: ЛЕНАНД. 2016. 282 с.
- Четверухин Н.Ф. Проективная геометрия. М.: Учпедгиз. 961. 360 с.
- Boissonnat J-D.,Teillaud M. Effective Computational Geometry for Curves and Surfaces With 120 Figures and 1 Table. Springer, 2006. 351 p.
- Brazil M, Zachariasen M. Optimal Interconnection Trees in the Plane Theory, Algorithms and Applications, Springer, 2015. 344 p.