ОБ ОСОБЕННОСТЯХ КОНСТРУКТИВНОГО РЕШЕНИЯ ЗАДАЧИ О СФЕРАХ ДАНДЕЛЕНА
Д.В.ВОЛОШИНОВ
Санкт-Петербургский государственный университет телекоммуникаций им. проф.М.А.Бонч-Бруевича (Санкт-Петербург)
denis.voloshinov@yandex.ru

THE PECULIARITY OF THE CONSTRUCTIVE SOLUTION OF DANDELEN SPHERES PROBLEM

Аннотация

Статья посвящена анализу задачи о сферах Данделена на основе конструктивного геометрического метода. В статье показано, что традиционный подход, применяемый к решению задачи, приводит к получению лишь ограниченного множества разнородных решений. Рассмотрение задачи в контексте проективных свойств плоскости и пространства методами конструктивной геометрии позволяет по-новому интерпретировать результаты этой задачи. В статье показано, что, решаемая задача имеет чисто проективную природу и может быть решена единым методом, чего невозможно добиться, если проводить рассуждения и строить доказательства только на положениях аффинной геометрии. Научная новизна исследования заключается в обнаружении и теоретическом обосновании нового классификационного признака, позволяющего причислить к классу сфер Данделена множества пар сфер, имеющих мнимые касания с квадрикой, а также пары мнимых сфер, имеющих единый принцип конструктивной взаимосвязи образов, наряду с действительными решениями. Практическая значимость работы заключается в расширении сфер применения методов конструктивного геометрического моделирования к решению задач, совершенствованию геометрической теории, развитии функциональных возможностей системы геометрического моделирования Симплекс для задач автоматизации проектирования объектов и процессов. Представленные в статье алгоритмы демонстрируют глубинную проективную природу и взаимосвязь таких задач, как задача об окружностях и сферах Аполлония, задача о сферах Данделена и других, а закладывает основу исследований в направлении многомерных интерпретаций этих задач. Решение задачи может быть полезно и для реализации функций сопряжений кривых второго порядка посредством окружностей в целях совершенствования инструментов автоматизации проектирования CAD-систем без применения для этих целей численных методов математики.

Abstracts

The article is devoted to the analysis of Dandelen spheres problem provided on the basis of the constructive geometric approach. The article shows that the traditional approach used to solve the problem leads to a limited set of heterogeneous solutions. Consideration of the problem in the context of projective properties of the plane and space by methods of structural geometry allows to interpret the results of this problem in a new way. The article shows that the solved problem has a purely projective nature and can be developed by a unified method, which is impossible to achieve while conduct reasoning and construct proofs only on the positions of affine geometry. The scientific novelty of the research is the discovery and theoretical justification of a new classification feature that allows to classify the set of pairs of spheres with imaginary tangents to the quadric, as well as pairs of imaginary spheres with a single principle of constructive interrelation of images, along with real solutions, to be included in the class of Dandelion spheres. The practical significance of the work lies in the extension of applications of constructive methods of geometric modeling to the solution of problems, the improvement of the geometric theory, the development of system functionality of geometric modeling Simplex for tasks of objects and processes design automation. The algorithms presented in the article demonstrate the deep projective nature and interrelation of such problems as the problem of circles and Apollonian spheres, the problem of Dandelion spheres and others, and determines the basis for research in the way of multidimensional interpretations of these problems. The solution of the problem can be useful for the realization of the functions of conjugation for curves of the second order by means of circles in order to improve the tools of CAD-systems design automation without the use of numerical methods of mathematics for this purpose.

Ключевые слова: геометрическое моделирование, проективная геометрия, мнимая геометрия, сферы Данделена, квадрика, кривая второго порядка, инволюция, коника, фокус, Симплекс.

Keywords: geometric modeling, projective geometry, imaginary geometry, Dandelen spheres, quadric, curve of second-order, involution, conic, focus, Simplex.

Задача о сферах Данделена является одной из наиболее известных геометрических задач, связывающей квадратичные образы трехмерного пространства и плоскости, имеющая изящную визуальную интерпретацию. Впервые геометрическая конструкция, обосновывающая существование двух сфер, касающихся прямого кругового конуса и пересекающей его плоскости, была получена Данделеном [1], а в дальнейшем, распространена и на другие разновидности квадрик [3, 6, 21, 23, 28].

В исходной постановке задача о шарах Данделена утверждает следующее: пусть дан прямой круговой конус; если конус пересекается плоскостью, то можно построить две сферы, единовременно касающиеся и конуса, и сферы, причем касание плоскости происходит в фокальных точках коники, возникающей от пересечения плоскости и конуса. Как уже было отмечено ранее, задача о сферах Данделена может быть распространена на случай произвольной квадрики вращения, а не только прямого кругового конуса, однако в этом случае сферы, касающиеся поверхности и плоскости в фокальных точках кривой сечения, существуют не всегда [13]. Задача данной статьи дать конструктивное [2] проективное обоснование решения задачи о сферах Данделена и показать, что к таким сферам следует причислять и иные сферы (как действительные, так и мнимые), которые выпадали из поля зрения исследователей данной задачи. Предлагаемое в статье обобщенное решение призвано продемонстрировать, что классификация объектов задачи должна осуществляться не на чисто визуальной оценке их композиции [23, 28], а на более глубоких взаимосвязях, проявляющих единый принцип их геометрического взаимодействия. В результате анализа алгоритма действия конструктивной геометрической схемы, являющейся причиной визуального причисления наблюдаемых сфер к объектам особого типа, будет сделан вывод о том, что класс объектов, называемых сферами Данделена, должен быть расширен сферами, ранее к таковым не причислявшимися.

На начальном этапе рассуждений рассмотрим конструктивный алгоритм построения сфер Данделена для квадрики вращения, используя для этих целей модель $G_{\mathrm{2,2}}^3$ – эпюр Монжа [5, 26]. Для анализа задачи будет достаточно построить только одну проекцию данной модели.

Пусть квадрика $\sigma$ будет задана очерком $s$ и осью вращения $i$ (рис. 1). Без потери общности плоскость сечения зададим следом $\alpha$ . Для определения местоположения фокальных точек, в которых сферы должны будут касаться плоскости, используем метод дополнительного ортогонального проецирования и построим кривую $a$ , возникающую от пересечения плоскости и квадрики. Результат такого пересечения – коника, для однозначного определения которой необходимо наличие пяти известных точек. Две из них ( $P_1$ и $P_2$ ) уже имеются, поскольку они образуются от пересечения следа плоскости и очерка $s$ . Для построения недостающих точек проведем следы двух вспомогательных плоскостей $\beta$ и $\gamma$ , ортогональных к оси вращения $i$ . Линии $b$ и $g$ пересечения плоскостей $\beta$ и $\gamma$ с поверхностью квадрики – суть окружности, диаметры которых определяются точками пересечения очерка квадрики со следами. Зная точки пересечения следа со следами $\alpha$ , $\beta$ и $\gamma$ , определим превышения точек ${\Delta }_b$ и ${\Delta }_g$ , которые необходимо отложить от этих точек по направлению, перпендикулярному к следу $\alpha$ . Таким образом, недостающие точки $P_3$ , $P_4$ и $P_5$ искомого конического сечения $a$ найдены.

Теперь при наличии самой коники $a$ не составит труда найти ее фокальные точки $F_1$ и $F_2$ , для чего можно использовать любой известный конструктивный алгоритм, например [30]. Поскольку прямая $\alpha$ является осью симметрии коники $a$ , то точки $F_1$ и $F_2$ сразу занимают необходимое для решения задачи положение. Для проведения очерков искомых сфер Данделена необходимо в точках $F_1$ и $F_2$ восстановить перпендикуляры к следу $\alpha$ и найти точки пересечения полученных прямых с осью вращения $i$ – центры сфер $C_1$ и $C_2$ , на чем определение очерков сфер $d_1$ и $d_2$ можно считать законченным.

Рис. 1. Построение сфер Данделена на эпюре Монжа

Анализ представленного алгоритма показывает, что при общей корректности, построение сфер ${\delta }_1$ и ${\delta }_2$ достигается не всегда. Причем представленная геометрическая конструкция не дает прямого обоснования причин «успешного» или «неудачного» исходов при построении сфер. В связи с этим проанализируем новую задачу, сформулированную в обратной постановке. Пусть заданы очерки двух сфер ${\delta }_1$ и ${\delta }_2$ (рис. 2). Исходя из предположения, что эти сферы изначально являются сферами Данделена, требуется построить очерк квадрики вращения $\sigma$ , удовлетворяющей условию прямой задачи. Данному условию соответствует множественное решение. Поскольку очерк-коника $\sigma$ будет касаться очерков сфер в четырех точках, то для управления ее формой требуется всего одна точка и, следовательно, мы имеем дело с однопараметрическим множеством решений [22].

Выберем управляющую точку $M$ на одной из общих касательных $t$ , проведенных к очеркам $d_1$ и $d_2$ сфер ${\delta }_1$ и ${\delta }_2$ . Рассматривая точку $M$ , как одну из двойных точек инволюции $\eta$ , индуцированной на прямой $\alpha$ пока еще не известной коникой $s$ , определим сопряженную с ней точку $M^{\prime }$ , получая ее в центральной симметрии относительно точки пересечения радикальной оси $r$ окружностей ${\delta }_1$ и ${\delta }_2$ и прямой $t$ . Используя точки $M$ и $M^{\prime }$ в качестве диаметральных, проведем через них вспомогательную окружность $v$ и, считая ее окружностью инверсии [4, 18, 20], преобразуем точки касания $F_1$ и $F_2$ в соответственные точки $H_1$ и $H_2$ , которые, собственно, и являются образами точек $F_1$ и $F_2$ в инволюции $\eta$ . Проведем через $H_1$ и $H_2$ прямые линии, перпендикулярные к оси $i$ , до пересечения с соответственными очерками $d_1$ и $d_2$ и получим точки $P_1$ , $P_2$ , $P_3$ , $P_4$ касания очерка $s$ коники $\sigma$ c очерками сфер. Полученная конструктивная схема позволяет получить однопараметрическое множество очерков $s$ , управляемых точкой $M$ при ее перемещении по прямой $t$ . Из анализа геометрической конструкции становится ясно, что построение точек касания квадрики и сфер основывается на действии изменяемого инволюционного соответствия, то есть представляет собой результат взаимодействия пучка инволюций с центрами, фиксированными в фокальных точках $F_1$ и $F_2$ .

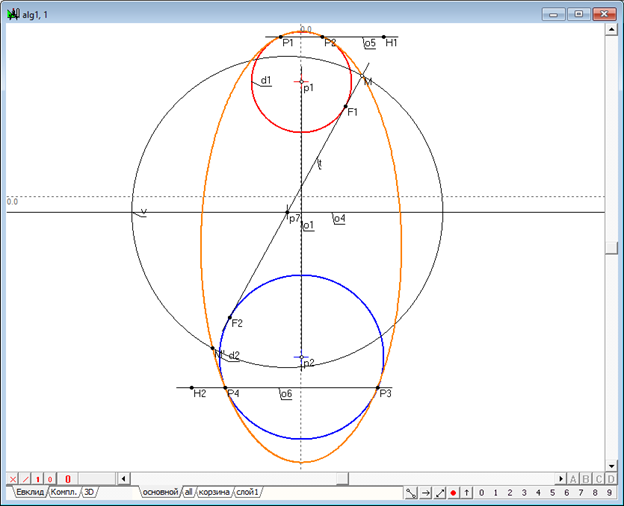
Рис. 2. Построение квадрики, касательной к двум заданным сферам

Без сомнения, проявление взаимодействий объектов под влиянием этого преобразования следует считать более общим, нежели выводы, сделанные только лишь посредством визуальной оценки позиционных отношений между сферами и квадрикой, наблюдаемых при традиционном решении задачи Данделена. Из сказанного с неизбежностью следует, что класс сфер, причисляемых к сферам Данделена, расширяется сферами, которые не имеют явного касания с поверхностью квадрики (т.е. действительных точек касания), но касаются ее мнимым образом (рис. 3).

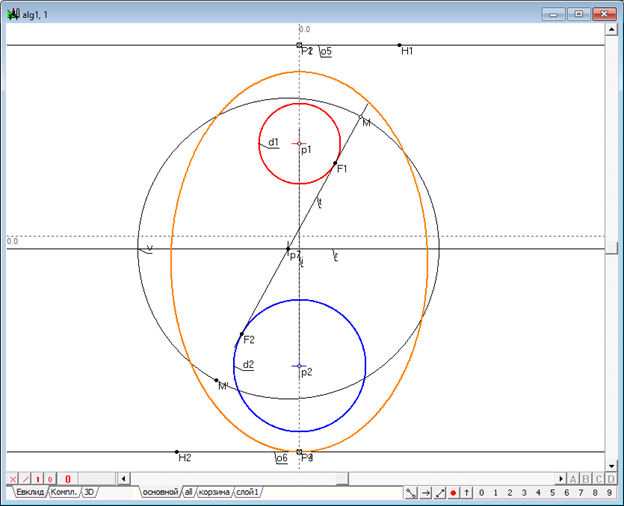
Рис. 3. Иллюстрация мнимого касания сфер и квадрики

Рассмотренная геометрическая схема, основанная на реализации проективных преобразований и соответствий [11, 16, 29], дает повод задуматься о постановке задачи Данделена и для сфер, имеющих мнимую природу, т.е. сфер, заданных комплекснозначными центрами и радиусами. Для обоснования возможности и корректности таких решений рассмотрим исходную постановку задачи о сферах Данделена вне контекста модели $G_{\mathrm{2,2}}^3$ , в которой предполагалось построение сечение квадрики плоскостью. Поставим перед собой иную цель: требуется построить кривую $f$ , являющуюся геометрическим местом фокальных точек [17], образованных сечением квадрики пучком параллельных плоскостей. Наличие такой кривой позволило бы отказаться от необходимости обращения к трехмерной интерпретации задачи и проводить все необходимые построения средствами плоской геометрической конструкции. Пусть на плоскости задан очерк $s$ квадрики $\sigma$ и задано направление на бесконечно удаленную точку $A^{\infty }$ , через которую проходят следы плоскостей $\left\{\alpha \right\}$ , рассекающих квадрику $\sigma$ (рис. 4). Найдем поляру $p$ точки $A^{\infty }$ относительно коники $s$ , определим точки $T_1$ и $T_2$ пересечения поляры $p$ с коникой $s$ и проведем две касательные $t_1=T_1\circ A^{\infty }$ и $t_2=T_2\circ A^{\infty }$ . Найдем также фокусы $Z_1$ и $Z_2$ коники $s$ . Искомая кривая $f$ , являясь кривой второго порядка, должна проходить через предельные точки $T_1$ и $T_2$ , в которых она является касательной к прямым $t_1$ и $t_2$ соответственно, а также через фокальные точки $Z_1$ или $Z_2$ (одна точка избыточна). Выбирая теперь произвольную прямую $\alpha$ из пучка $\left\{\alpha \right\}$ , мы можем определить положение фокальных точек $F_1$ и $F_2$ , не прибегая к модели $G_{\mathrm{2,2}}^3$ , и построить их, как результат пересечения прямой $\alpha$ с коникой $s$ : $F_1,F_2=\alpha \times f$ . Восстановив перпендикуляры к $\alpha$ в точках $F_1$ и $F_2$ , получаем в их пересечении с осью $i$ точки $S_1$ и $S_2$ – центры очерков $d_1$ и $d_2$ сфер Данделена.

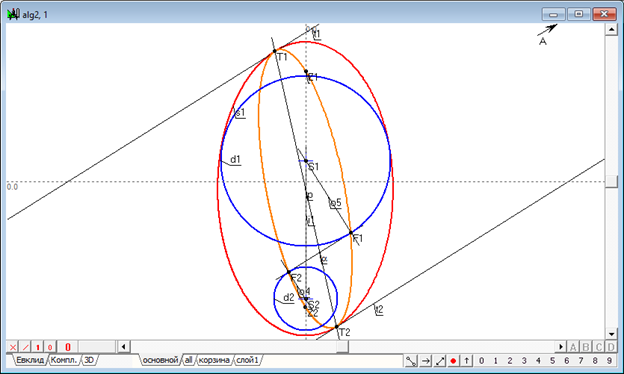
Рис. 4. Построение коники, несущей фокальные точки сечения

Представленная на рис. 4 схема позволяет не только строить ранее известные сферы Данделена для произвольных квадрики и плоскости, но и определяет путь выхода этой задачи за рамки действительных решений. В тех случаях, когда прямая $\alpha$ оказывается за пределами диапазона, ограниченного линиями $t_1$ и $t_2$ , полученная геометрическая конструкция порождает решения с мнимыми образами (рис. 5). Ввиду идентичности способа образования действительных сфер с мнимыми сферами, последние также следует соотносить с классом сфер, именуемых сферами Данделена.

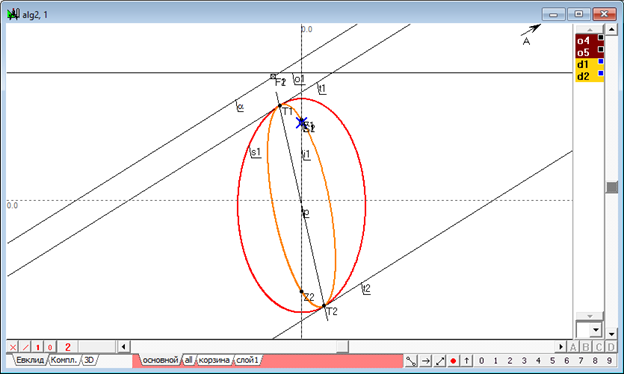
Рис. 5. Иллюстрация принципа образования мнимых решений задачи Данделена

Обнаруженное присутствие мнимых образов в решениях задачи о сферах Данделена побуждает обратиться еще к одной неизученной стороне этого геометрического феномена. Поскольку любая кривая второго порядка обладает четырьмя фокальными точками, одна пара из которых представлена действительными точками, а вторая пара – мнимыми, которые обычно упускаются из вида [12, 25]. В известных решениях задачи Данделена мнимые фокусы сечений квадрики плоскостью не рассматривались. Наличие мнимых фокальных точек у коники подтверждается известным геометрическим построением, суть которого пояснена на чертеже. Равнозначность коник в проективной геометрии влечет за собой и равнозначность их главных диаметров. Следовательно, равнозначным должен быть и принцип построения фокальных точек. Действительно, проведя окружность $u$ с центром $P_3$ через точку $K$ , в пересечении $u$ с главным диаметром $P_1\circ P_2$ находим фокальные точки $F_1$ и $F_2$ . В приведенном примере на рис. 6 эти точки действительные. В свою очередь, окружность $v$ с центром $P_1$ , проведенная через ту же точку $K$ , пересекает главный диаметр $P_3\circ P_4$ в точках $F_3$ и $F_4$ (рис. 6).

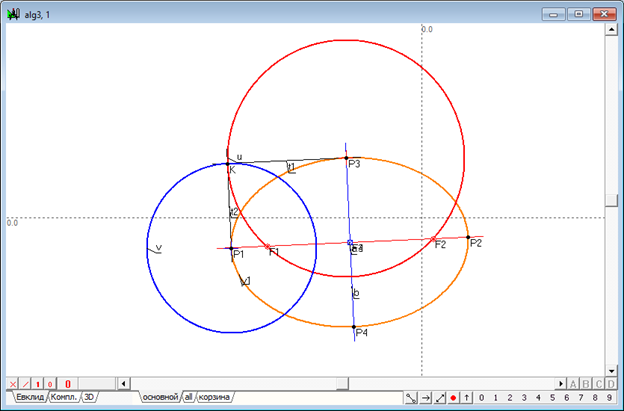
Рис. 6. Схема построения действительных и мнимых фокусов коники

Теоретически, по отношению к точкам $F_3$ и $F_4$ может быть применен алгоритм построения сфер Данделена, рассмотренный ранее в данной статье. Не претерпевая каких-либо изменений по сути, он будет отличаться лишь своими результатами: получаемые результаты будут существенно связаны с мнимыми образами геометрии [14, 15, 19, 24, 27]. Действие алгоритма, иллюстрация которого в настоящий момент затруднительна по причине отсутствия в системе Симплекс [7–10] некоторых необходимых для моделирования комплекснозначных функций, должно привести к образованию еще одной пары сфер, которые по признакам своего «порождения» также должны быть отнесены к классу сфер Данделена. Детальное изложение алгоритма и демонстрация геометрических свойств, возникающих при решении данной задачи, представляет собой самостоятельную задачу, требующую совершенствования геометрической системы, и выходит за рамки настоящей статьи. Таким образом, в статье представлен новый единый подход к решению задачи о сферах Данделена, определенных на осесимметричных квадриках. На основе проведенного анализа показано, что существующая в настоящее время классификация сфер Данделена несовершенна, поскольку она основывается на визуальном восприятии результата и аффинных геометрических представлениях. В статье раскрыта проективная природа данной задачи и показан геометрически механизм образования искомых сфер. Единая геометрическая схема позволила подойти к классификации сфер с конструктивных позиций, включая в нее объекты, порождаемые как за счет образования мнимых образов, так и имеющих собственную мнимую природу. Полученные результаты послужили теоретической и практической основой для совершенствования функциональных возможностей системы геометрического моделирования Симплекс.

Теоретически, по отношению к точкам и может быть применен алгоритм построения сфер Данделена, рассмотренный ранее в данной статье. Не претерпевая каких-либо изменений по сути, он будет отличаться лишь своими результатами: получаемые результаты будут существенно связаны с мнимыми образами геометрии [14, 15, 19, 24, 27]. Действие алгоритма, иллюстрация которого в настоящий момент затруднительна по причине отсутствия в системе Симплекс [7–10] некоторых необходимых для моделирования комплекснозначных функций, должно привести к образованию еще одной пары сфер, которые по признакам своего «порождения» также должны быть отнесены к классу сфер Данделена. Детальное изложение алгоритма и демонстрация геометрических свойств, возникающих при решении данной задачи, представляет собой самостоятельную задачу, требующую совершенствования геометрической системы, и выходит за рамки настоящей статьи. Таким образом, в статье представлен новый единый подход к решению задачи о сферах Данделена, определенных на осесимметричных квадриках. На основе проведенного анализа показано, что существующая в настоящее время классификация сфер Данделена несовершенна, поскольку она основывается на визуальном восприятии результата и аффинных геометрических представлениях. В статье раскрыта проективная природа данной задачи и показан геометрически механизм образования искомых сфер. Единая геометрическая схема позволила подойти к классификации сфер с конструктивных позиций, включая в нее объекты, порождаемые как за счет образования мнимых образов, так и имеющих собственную мнимую природу. Полученные результаты послужили теоретической и практической основой для совершенствования функциональных возможностей системы геометрического моделирования Симплекс

1. Dandelin G. Mémoire sur l’hyperboloïde de révolution, et sur les hexagones de Pascal et de M. Brianchon // Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Bruxelles, V. III., 1826 (pp. 3–16).
2. Адлер А. Теория геометрических построений. – Л.: Учпедгиз. – 1940. – 232 с.
3. Акопян А.В., Заславский А.А. Геометрические свойства кривых второго порядка. – М.: МЦНМО. – 2007. – 136 с.
4. Бакельман И.Я. Инверсия. – М.: Наука. – 1966. – 79 с.
5. Вальков К.И. Введение в теорию моделирования. – Л.: ЛИСИ. – 1974. – 152 с.
6. Васильева В.Н., Хейфец А.Л. Реализация обобщенной теоремы Данделена для произвольных квадрик вращения в AutoCAD [Текст] / В.Н. Васильева, А.Л. Хейфец // Геометрия и графика. – 2014. – Т.2 – С. 9–14. DOI: 10.12737/5584.
7. Волошинов Д.В. Геометрическая лаборатория. Новый геометрический инструмент. URL: http://dgng.pstu.ru/conf2017/papers/60.
8. Волошинов Д.В. О перспективах развития геометрии и ее инструментария / Д.В. Волошинов // Геометрия и графика. – 2014. – Т. 1 – № 1. – C. 15–21. DOI: 10.12737/3844.
9. Волошинов Д.В., Соломонов К.Н. Конструктивное геометрическое моделирование как перспектива преподавания графических дисциплин / Д.В. Волошинов, К.Н. Соломонов // Геометрия и графика. – 2013. – Т. 1 – № 2. – C. 10–13. DOI: 10.12737/778.
10. Волошинов Д.В. Конструктивное геометрическое моделирование. Теория, практика, автоматизация: монография / Д.В. Волошинов. – Saarbrücken: Lambert Academic Publishing, 2010. – 355 c.
11. Вольберг А.О. Основные идеи проективной геометрии. – М.-Л.: Учпедгиз. – 1949. – 188 c.
12. Гильберт Д., Кон-Фоссен C. Наглядная геометрия. – М.-Л.: ОНТИ. – 1936. – 304 с.
13. Гирш А.Г. Задание и построение квадрики / А.Г. Гирш // Геометрия и графика. – 2017. – Т. 5 – № 2. – C. 39–44. DOI: 10.12737.
14. Гирш А.Г. Мнимости в геометрии / А.Г. Гирш // Геометрия и графика. – 2014. – Т. 2 – № 2. – C. 9–14. DOI: 10.12737/5583.
15. Гирш А.Г. Наглядная мнимая геометрия: монография / А.Г. Гирш. – М.: ООО ИПЦ «Маска», 2008. – 216 с.
16. Глаголев Н.А. Проективная геометрия. – М.: Высшая школа. – 1963. – 342 с.
17. Дорфман А.Г. Оптика конических сечений. – М.: Физматгиз. – 1959. – 32 с.
18. Жижилкин И.Д. Инверсия. – М.: Изд-во МЦНМО. – 2009. – 72 с.
19. Иванов Г.С., Дмитриева И.М. О задачах начертательной геометрии с мнимыми решениями / Г.С. Иванов, И.М. Дмитриева // Геометрия и графика. – 2015. – Т. 3 – № 2. – C. 3–8. DOI: 10.12737/12163.
20. Коксетер Г.С.М., Грейтцер С.П. Новые встречи с геометрией. – М.: Наука. – 1978. – Т. 14. – 224 с.
21. Короткий В.А. Двойное прикосновение в пучке поверхностей второго порядка [Текст] / В.А. Короткий// Геометрия и графика. – 2014. – Т.1 – С. 9–14. DOI: 10.12737/3843.
22. Литцман В. Старое и новое о круге [Текст] / Пер. с нем. В.С. Бермана. – М.: Физматгиз. – 1960. – 60 с.
23. Логиновский А.Н., Хейфец А.Л. Решение задач на основе параметризации в пакете AutoCAD [Текст] / А.Н. Логиновский, А.Л. Хейфец // Геометрия и графика. – 2013. – Т.2 – С. 61–64. DOI: 10.12737/793.
24. Пеклич В.А. Мнимая начертательная геометрия: учебное пособие / В.А. Пеклич. –М.: Изд-во АСВ. – 2007. – 104 с.
25. Розенфельд Б.А. Аполлоний Пергский. – М.: МЦНМО. – 2004. – 176 с.
26. Соболев Н.А. Общая теория изображений: учеб. Пособие для вузов. – М.: «Издательство «Архтектура С». – 2004. – 672 с.
27. Флоренский П.А. Мнимости в геометрии. Расширение области двухмерных образов геометрии (опыт нового истолкования мнимостей). – М.: «Лазурь». – 1991. – 96 с.
28. Хейфец А.Л. Коники как сечения квадрик плоскостью (обобщенная теорема Данделена) / А.Л. Хейфец // Геометрия и графика. – 2017. – Т. 5. – № 2. – C. 45–58.
29. Четверухин   Н.Ф.   Проективная   геометрия. – М.:  Просвещение. – 1953. – 360 с.
30. Шаль М. О способе построения фокусов и доказательства их свойств на косом конусе // Исторический обзор происхождения и развития геометрических методов. – М. – 1883. – 307 с.

.

Literature

1. Dandelin G. Mémoire sur l ' hyperboloïde de révolution, et sur les hexagones de Pascal et de M. Brianchon / Nouveaux mémoires de l'académie Royale des Sciences et Belles-Lettres de Bruxelles, T. III., 1826 (pp. 3–16).
2. Adler A. Teorija geometricheskih postroenij. – L.: Uchpedgiz. – 1940. – 232 p.
3. Akopyan A.V., Zaslavsky A.A. Geometricheskie svojstva krivyh vtorogo porjadka. – M.: MCNMO.  – 2007. – 136 p.
4. Bakelman I. Ya. Inversija. – M.: Nauka. – 1966. – 79 p.
5. Valkov K.I. Vvedenie v teoriju modelirovanija. – L.: LISI. – 1974. – 152 p.
6. Vasilievа V.N., Heifetz A.L. Realizacija obobshhennoj teoremy Dandelena dlja proizvol'nyh kvadrik vrashhenija v AutoCAD [Text] / V.N. Vasilievа, A.L. Kheifets // Geometry and graphics. – 2014. – Vol. 2 – Pp. 9–14. DOI: 10.12737/5584.
7. Voloshinov D.V. Geometricheskaja laboratorija. Novyj geometricheskij instrument.  URL: http://dgng.pstu.ru/conf2017/papers/60.
8. Voloshinov D.V. O perspektivah razvitija geometrii i ee instrumentarija / D.V. Voloshinov // Geometry and graphics. – 2014. – Vol. 1 – № 1. – Pp. 15-21. DOI: 10.12737/3844.
9. Voloshinov D.V., Solomonov K.N. Konstruktivnoe geometricheskoe modelirovanie kak perspektiva prepodavanija graficheskih disciplin / D.V. Voloshinov, K.N. Solomonov // Geometry and graphics. – 2013. – Vol. 1 – № 2. – Pp. 10-13. DOI: 10.12737/778.
10. Voloshinov D.V. Konstruktivnoe geometricheskoe modelirovanie. Teorija, praktika, avtomatizacija: monograph / D.V. Voloshinov. – Saarbrücken: Lambert Academic Publishing. – 2010. – 355 p.
11. Volberg A.O. Osnovnye idei proektivnoj geometrii. – M.-L.: Uchpedgiz. – 1949. – 188 p.
12. Hilbert D., Cohn-Vossen C. Nagljadnaja geometrija. – M.-L.: ONTI. – 1936. – 304 p.
13. Hirsch A.G. Zadanie i postroenie kvadriki / A.G. Hirsch // Geometry and graphics. – 2017. – Vol. 5 – № 2. – Pp. 39–44. DOI: 10.12737.
14. Hirsh A.G. Mnimosti v geometrii / A.G. Hirsh // Geometry and graphics. – 2014. – Vol. 2 – № 2. – Pp. 9–4. DOI: 10.12737/5583.
15. Hirsh A.G. Nagljadnaja mnimaja geometrija: monograph / A.G. Hirsh. – M.: «Mask», – 2008. – 216 p.
16. Glagolev N.A. Proektivnaja geometrija. – M.: Higher school. – 1963. – 342 p.
17. Dorfman A.G. Optika konicheskih sechenij. M.: Fizmatgiz. – 1959. – 32 p.
18. Zhizhilkin I.D. Inversija. – M.: MTSNMO. – 2009. – 72 p.
19. Ivanov G.S., Dmitrieva I.M. O zadachah nachertatel'noj geometrii s mnimymi reshenijami / G.S. Ivanov, I.M. Dmitrieva // Geometry and graphics. – 2015. – Vol. 3 – № 2. – Pp. 3–8. DOI: 10.12737/12163.
20. Coxeter G.S.M., Greitzer S.P. Novye vstrechi s geometriej. – M.: Nauka. – 1978. – Vol. 14. – 224 p.
21. Litzman V. Staroe i novoe o kruge [Text] / Ed. with V. S. Berman. – M.: Fizmatgiz. – 1960. – 60 p.
22. Korotky V.A. Dvojnoe prikosnovenie v puchke poverhnostej vtorogo porjadka [Text] / V.A. Korotky, // Geometry and graphics. – 2014. – Vol. 1 – Pp. 9-14. DOI: 10.12737/3843
23. Loginovsky A.N., Kheifetz A.L., Reshenie zadach na osnove parametrizacii v pakete AutoCAD [Text] / A.N. Loginovsky, A.L. Kheifets // Geometry and graphics. – 2013. – Vol. 2 – Pp. 61–64. DOI: 10.12737/793.
24. Peklich V.A. Mnimaja nachertatel'naja geometrija: textbook / V.A. Peklich. – M.: Publishing house of ASB. – 2007. – 104 p.
25. Rosenfeld B.A. Apollonij Pergskij. – M.: MCNMO. 2004. – 176 p.
26. Sobolev N.A. Obshhaja teorija izobrazhenij. The manual for high schools. – M.: «Publishing House «Archtecture C». – 2004. – 672 p.
27. Florensky P.A. Mnimosti v geometrii. Rasshirenie oblasti dvuhmernyh obrazov geometrii (opyt novogo istolkovanija mnimostej). – M.: «Lazur». – 1991. – 96 p.
28. Kheifetz A.L. Koniki kak sechenija kvadrik ploskost'ju (obobshhennaja teorema Dandelena) / A.L. Kheifets//Geometry and graphics. – 2017. – Vol. 5. – № 2. – C. 45–58.
29. Chetverukhin N.F. Proektivnaja   geometrija. – M.: Prosveshenie. – 1953. – 360 p.
30. Shal M. O sposobe postroenija fokusov i dokazatel'stva ih svojstv na kosom konuse // Historical review of the origin and development of geometric methods. – M.: 1883.