ОБ УТОЧНЕНИИ НЕКОТОРЫХ ПОНЯТИЙ ПРОЕКТИВНОЙ ГЕОМЕТРИИ

Д.В.ВОЛОШИНОВ
Санкт-Петербургский государственный университет телекоммуникаций им. проф.М.А.Бонч-Бруевича (Санкт-Петербург)
denis.voloshinov@yandex.ru

Аннотация
Статья посвящена разработке рассмотрению нескольких геометрических конструкций, связанных с построением радикальной оси двух окружностей. Геометрические свойства, обнаруживающиеся в этих конструкциях, позволяют сделать ряд обобщений и уточнений в определении такого понятия, как радикальная ось, окружность бесконечно большого радиуса, преобразование n-мерного пространства в инверсии относительно сфер размерности n.

Ключевые слова: радикальная ось, инволюция в точечных рядах, инверсия, конструктивная геометрия, геометрическое моделирование, Симплекс.

Введение

Геометрические объекты, которые получили название радикальных пространств, играют важную роль в решении многих геометрических задач, в частности, задач сопряжения n-мерных сфер в пространствах n измерений. Понятие «радикальный» тесно связан с понятием степени точки относительно некоторой выбранной n-сферы [1]. В плоскости под радикальной осью двух окружностей обычно понимают линию, несущую на себе точки, проявляющие одинаковую степень по отношению к этим окружностям. В литературе указывается, что данная линия является обычной прямой линией. Несложно показать, что получаемая линия проходит через точки пересечения окружностей, причем, если это пересечение явное, то прямая проходит через действительные точки пересечения; если же явного пересечения нет, то радикальная ось проходит через две мнимые комплексно-сопряженные точки определяющих ее окружностей. Существует несложное геометрическое построение, которое позволяет путем введения дополнительной третьей окружности, явно пересекающей исходные, построить радикальную ось, не используя при этом точки пересечения исходных окружностей. Поэтому, для окружностей, имеющих вещественные центр и радиус, построение радикальной оси даже вручную не составляет особого труда.

Общепринятое определение радикальной оси основывается на метрических понятиях геометрии. Однако при разработке средств автоматизации проектирования конструктивных геометрических моделей требуется учитывать не только метрические, но и глубинные проекционные свойства плоскости, поскольку проекционные преобразования геометрических образов не должны быть подвержены каким-либо исключениям, противоречащим общим положениям теории.  Ситуация усугубляется, если задача построения радикальной оси ставится в отношении окружностей, хотя бы одна из которых определена на мнимом центре или радиусе.

Ответ на вопрос, какой линией будет представлена радикальная ось, существует ли она вообще и как ее построить, если она действительно существует, требует дополнительного изучения, поскольку ответы на подобные вопросы без дополнительного экспериментирования с геометрическими моделями в вопросах автоматизации не всегда очевидны. Более того, нельзя исключить вероятность того, что, несмотря на кажущуюся простоту и очевидность алгоритмов построения радикальной оси, за этим понятием скрываются и иные, нежели прямая линия, образы. Такие ситуации могут иметь место в тех случаях, когда из виду упускаются свойства бесконечно удаленных образов, неопределенности, вырождения или иные геометрические явления, подобные перечисленным. Анализ ряда алгоритмов и преобразований, проведенных автором статьи, позволил сделать заключение о том, что проявления свойств радикальной оси в конструктивной геометрической связи с определяющими ее объектами изучены недостаточно полно. Полученные результаты основываются не на аналитическом описании задачи, а на исследовании поведения обобщенных геометрических схем и взаимодействия их объектов. Из результатов следует неожиданный вывод: радикальная ось не является прямой линией в обычном понимании. Геометрические эксперименты [2–4] с конструктивными моделями показывают, что радикальная ось ­– это некая «предельная» окружность особого рода, геометрическая интерпретация которой возможна за счет единения двух прямых линий: собственной и бесконечно удаленной, причем несобственную точку «пересечения» этих прямых следует трактовать, как двойную.

Естественно, полученный результат становится возможным транзитивно распространить и на пространства многих измерений.

Особенности построения радикальной оси

Рассмотрим способ построения радикальной оси как прямой линии, проходящей через точки пересечения двух исходных окружностей. Пусть окружности $a$  и $b$  пересекаются в двух точках $P$  и $Q$ ,  а радикальная ось $x$  проходит через эти точки. Тогда, выбрав на плоскости точку  $M$  такую, что  $M\cancel{\subset }a;M\cancel{\subset }b;M\cancel{\subset }x$ , мы вправе провести через нее окружность $m:P\subset m;Q\subset m;M\subset m$ . При этом радикальная ось $x$  является таковой для любой пары окружностей, построенной на множестве $\left\{a,b,m\right\}$ . Таким образом, произвольной точке $M$  ставится одна единственная окружность из пучка окружностей с центрами   $P$  и   $Q$  (рис. 1).

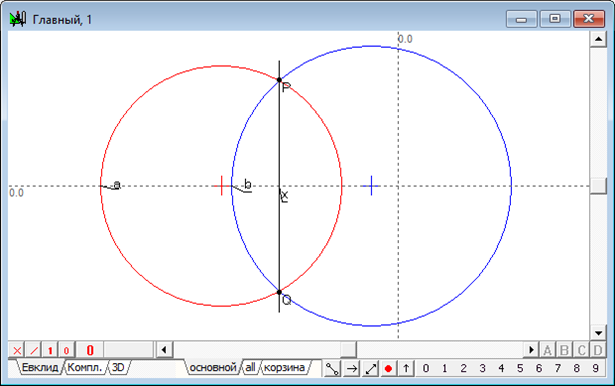
Рис.1. Радикальная ось как прямая, проходящая через точки пересечения окружностей.

Обращает на себя внимание тот факт, что ось $x$ является одним из компонентов этого пучка. Причем ее образ может быть получен в тех случаях, если точка $M$  располагается на $x$ , в результате чего говорят, что окружность вырождается в прямую линию. Но этого же результата можно добиться, если точку $M$  расположить на бесконечно удаленной прямой, замыкающей плоскость на себя. Причем сделать это можно, перемещая точку $M$  в бесконечность по любому направлению. С одной стороны, мы приходим к выводу о том, что окружность бесконечно большого радиуса выродилась в прямую, с другой стороны, мы предстаем перед фактом, что эта прямая будет проведена через три точки, не лежащие на одной прямой. Получаемое логическое противоречие является весомым аргументом к тому чтобы, задуматься о геометрической природе объекта, ассоциируемого с понятием радикальной оси.

Второе соображение основывается на том, что любой пучок окружностей в пересечении с произвольной прямой линией $l$ , образует на каждом элементе этого пучка пару точек (вещественных или мнимых), которые, являются двойными точками инволюций, индуцированных окружностями пучка в точечных рядах на линии $l$ . Более того, рассматривая прямую $l$ , как одномерное пространство, мы можем сделать еще одно важное обобщение: возникающая точечная пара в своем единстве – суть окружность одномерного пространства.  Однако, понимая под элементом $x$  прямую линию, мы получаем в пересечении с прямой $l$  лишь единственную точку (рис. 2), что является причиной нарушения общей закономерности. В этом случае не возникает повода говорить и об «одномерной» окружности.

Рис.2. Проявление конструктивной «неоднородности» пучка окружностей.

Однако, можно заметить, что, если к существующей в общепринятом смысле радикальной оси причислить несобственную прямую плоскости, возникающее логическое несоответствие устраняется. Действительно, точек пересечения прямой $l$  с реконструированным объектом становится две и, что более важно, на получаемых точках в парах окружностей можно построить инволюционное соответствие в рядах точек прямой $l$. Несложно показать, что двойные точки любых таких инволюционных соответствий одинаковы, в том числе и на точках, полученных от пересечения прямой $l$  с прямой $x$  и с бесконечно удаленной прямой (рис. 3).

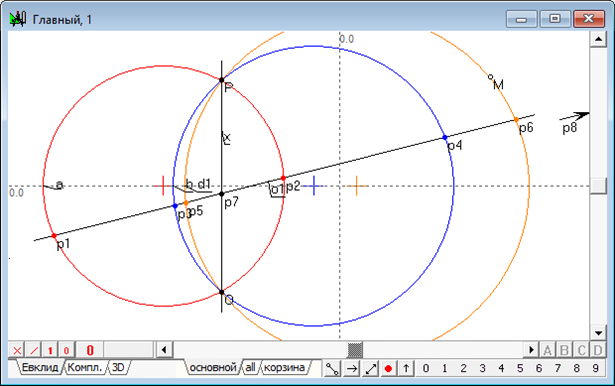
Рис.3. Иллюстрация дополнения радикальной оси бесконечно удаленной прямой.

Наблюдаемый результат можно трактовать и следующим образом. Как известно, все окружности плоскости, являясь частным (аффинным) проявлением кривых второго порядка, проходят через две фиксированные мнимые циклические точки, находящиеся на бесконечно удаленной прямой. Тогда радикальная ось, дополненная бесконечно удаленной прямой, с одной стороны, является окружностью, поскольку проходит через две циклические точки. В то же время радикальная ось проявляет свойства предельной вырожденной гиперболы, обычно интерпретируемой двумя «пересекающимися» прямыми линиями, одна из которых совпадает с бесконечно удаленной прямой.

Конструктивная равноценность «ветвей» радикальной оси

Покажем теперь, что с точки зрения конструктивного подхода к решению задач обе «ветви» расширенной радикальной оси равнозначны. Для этого решим задачу преобразования двух конических сечений в окружности и найдем две коллинеации, осуществляющие такие преобразования.

Пусть на плоскости заданы две коники $f$ и $g$ . Эти коники индуцируют в плоскости два поляритета. Переведем коники в поляритетах относительно друг друга в коники $f^{\prime }$ и $g^{\prime }$ (рис. 4).

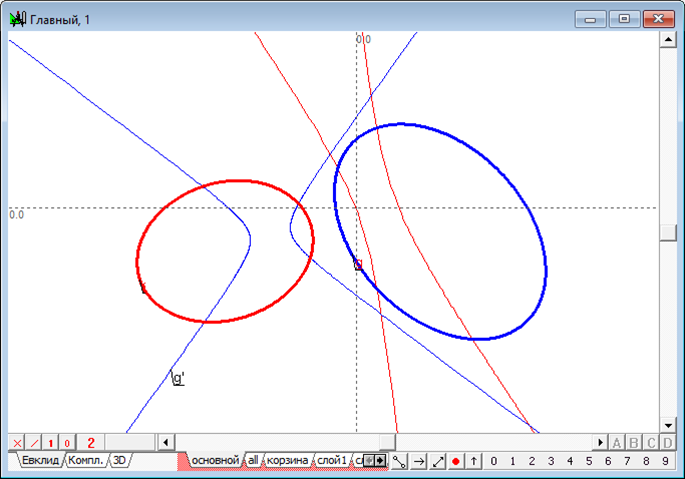
Рис.4. Исходные дачи к решению задачи о преобразовании двух коник в окружности.

Найдем точки пересечения коник$A_1,A_2,A_3,A_4=f\times g^{\prime }$ . Строя на точках $A_1,A_2,A_3,A_4$ четырехвершинник, определим положение точек $A$ , $B$  и $C$  – вершин автополярного треугольника, равнозначно индуцируемого обеими кониками $f$  и $g$ .

Проведем через вершины $A$  и $B$ прямую $ab=A\circ B$  и построим точки пересечения этой прямой с исходными кониками: $P_1,P_2=f\times ab$  и $Q_1,Q_2=g\times ab$ . Найдем также центры коник $f$  и $g$ : соответственно $P$  и $Q$ . Через бесконечно удаленную точку $T^{\infty }$  прямой $ab$  и точку $C$  проведем прямую $a{b}^{\prime }$  (рис. 5).

Рис.5. Построение вершин автополярного треугольника.

На двух наборах объектов$\left(P_1,P,P_2,a{b}^{\prime },C\right)$  и $\left(Q_1,Q,Q_2,a{b}^{\prime },C\right)$ построим коники $m$  и $n$ , полагая что прямая $a{b}^{\prime }$  является общей касательной к этим коникам в точке $C$  (рис. 6).

Рис.6. Построение вспомогательных коник $m$  и $n$ .

Имея общую двойную точку, коники $m$  и $n$  пересекаются в двух различных точках $U,V=m\times n$ .  Соединим точку $C$  с точками $U$  и $V$  прямыми линиями $u=C\circ U$  и $v=C\circ V$  (рис. 7). Прямые $u$  и $v$  проходят через точки пересечения коник $f$  и $g$ (в примере мнимые), а это значит, что обе коники индуцируют на этих прямых пару одинаковых инволюционных соответствий ${\eta }_u$  и ${\eta }_v$ .

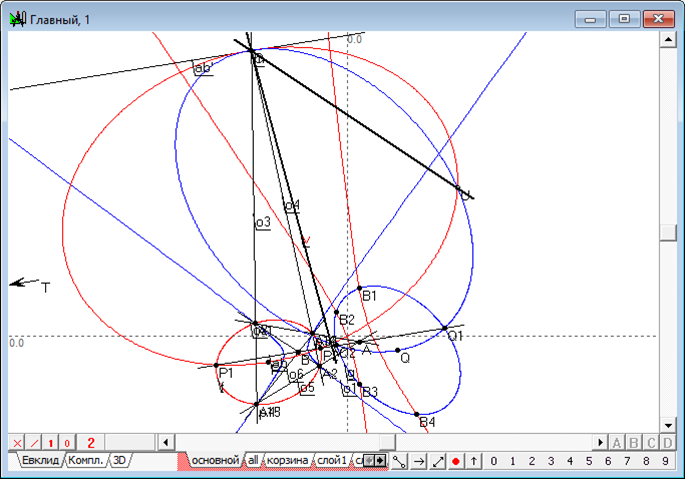
Рис.7. Прямые равных инволюций, индуцируемых исходными кониками.

Для определения коллинеаций, переводящих пару коник в пару окружностей, необходимо построить две пары точек Лагерра для прямых $u$  и $v$  соответственно. Это несложно сделать, переведя пару произвольных точек на каждой из прямых $u$  и $v$  в их образы в соответственных инволюциях ${\eta }_u$  и ${\eta }_v$  и построив на образах и прообразах этих точек, взятых как диаметральные, по паре окружностей. Точки пересечения соответственных окружностей и будут являться точками Лагерра, на которых следует построить две необходимые гомологии. Выполним эти действия раздельно для каждой их прямых $u$  и $v$ .

Возьмем на прямой $u$ две произвольные точки $U_1$ и $U_2$ построим их образы: $U_1{}^{\prime }={\eta }_u(U_1)$ и $U_2{}^{\prime }={\eta }_u(U_2)$ . Точки Лагерра $L{U}_1$ и $L{U}_2$ получим, как результат пересечения двух окружностей, построенных на парах точек $\left(U_1-U_1{}^{\prime }\right)$ и $\left(U_2-U_2{}^{\prime }\right)$ , взятых в качестве диаметральных.

Выберем на прямой $u$ две произвольные точки $R_1$  и $R_3$  и, спроецировав их, например, из центра $L{U}_1$  на бесконечно удаленную прямую, получим, соответственно, точки $R_2$  и $R_4$ . Проведем также прямую линию $u^{\prime }\parallel u$ , на которой выберем две произвольные точки $S_1$  и $S_2$ . Выбранный набор геометрических объектов позволяет задать гомологию ${\chi }_u|\begin{array}{c}{R}_1,S_1,R_2,S_2\\ R_3^{\infty },S_1,R_4^{\infty },S_2\end{array}$ , переводящую пару коник $f$  и $g$  в две соответствующие им окружности $f_u$  и $g_u$ . При этом коллинеация ${\chi }_u$  переводит прямую $v$  в линию $x_v$ , а линию $u$  в бесконечно удаленную прямую, то есть «расширенную» радикальную ось окружностей $f_u$  и $g_u$  (рис. 8).

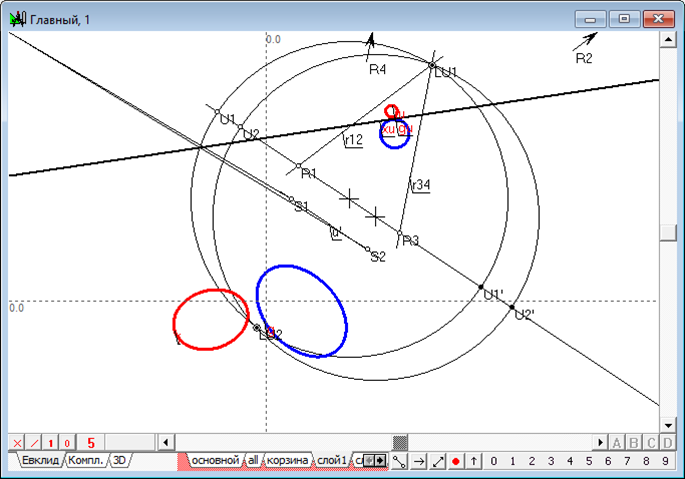
Рис.8. Построение двух окружностей и их радикальной оси с помощью коллинеации, определенной прямой $u$ .

Второе построение аналогично первому лишь с той разницей, что оно выполняется относительно прямой $v$ . Уже не рассматривая его подробно, отметим лишь, что коллинеация ${\chi }_v|\begin{array}{c}{K}_1,S_3,K_2,S_4\\ K_3^{\infty },S_3,K_4^{\infty },S_4\end{array}$  переводит прямую $u$  в линию $x_u$ , а линию $v$  в бесконечно удаленную прямую, то есть «расширенную» радикальную ось окружностей $f_v$  и $g_v$  (рис. 9).

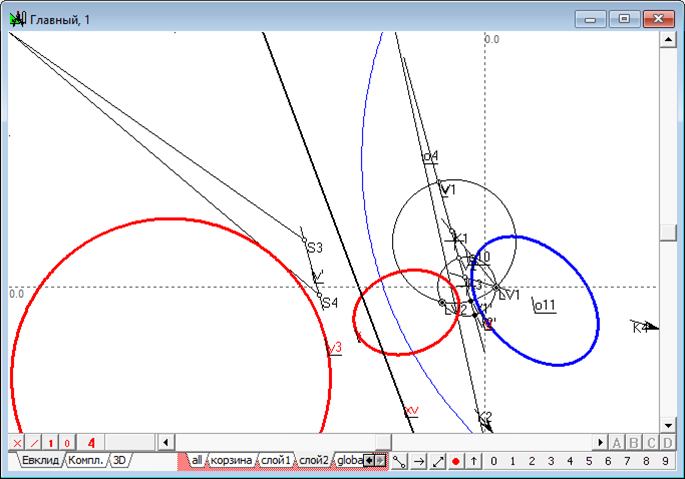
Рис.9. Построение двух окружностей и их радикальной оси с помощью коллинеации, определенной прямой $v$ .

Из приведенных построений видно, что они конструктивно равнозначны, следовательно, предположение о том, что понятие радикальной оси допускает расширенное толкование, подтверждается единством подхода к реализации общей геометрической модели трансформации коник в окружности, можно считать правомерным.

Заключение

В результате проведенного исследования и проведенных экспериментов с конструктивными моделями выработаны рекомендации по изменению и расширению функционального состава системы геометрического моделирования Симплекс [5], позволившие устранить возникавшие из-за неполноты теории исключения при решении задач, основанных на понятии радикальных пространств.

Литература

1. Бакельман И.Я. Инверсия. М.: Наука. 1966, 79 с.
2. Волошинов Д.В. Геометрическая лаборатория. Закладываем основы // Качество графической подготовки: проблемы, традиции и инновации: Материалы VII международной  Интернет-конференции.  Февраль - март 2017 г. Пермь, 2017.
3. Волошинов Д.В. Геометрическая лаборатория. Инструменты ортогональности // Качество графической подготовки: проблемы, традиции и инновации: Материалы VII международной  Интернет-конференции.  Февраль - март 2017 г. Пермь, 2017.
4. Волошинов Д.В. Геометрическая лаборатория. Новый геометрический инструмент // Качество графической подготовки: проблемы, традиции и инновации: Материалы VII международной  Интернет-конференции.  Февраль - март 2017 г. Пермь, 2017.
5. Волошинов Д.В. Конструктивное геометрическое моделирование. Теория, практика, автоматизация: монография / Д.В.Волошинов. – Saarbrücken: Lambert Academic Publishing, 2010. – 355 c.